工程陶瓷脆性域旋转超声磨削加工切削力研究

魏士亮，赵 鸿，薛 开，荆君涛，2

（1.哈尔滨工程大学机电工程学院，黑龙江哈尔滨150001；2.航天科工哈尔滨风华有限公司，黑龙江哈尔滨154001）

工程陶瓷脆性域旋转超声磨削加工切削力研究

魏士亮1，赵 鸿1，薛 开1，荆君涛1，2

（1.哈尔滨工程大学机电工程学院，黑龙江哈尔滨150001；2.航天科工哈尔滨风华有限公司，黑龙江哈尔滨154001）

为了解决由于工艺参数取值范围和实验次数有限而造成的实验结果局限性，对工程陶瓷脆性域旋转超声磨削加工切削力进行了研究。在旋转超声磨削加工机理研究基础上，结合弹塑性力学和压痕断裂力学，采用动量定理和动能定理，推导了单个金刚石端面加工和侧面加工切削力计算公式，并建立了工程陶瓷脆性域旋转超声磨削加工切削力数学模型。最后通过实验对切削力数学模型进行验证，结果表明：切削力模型计算值与实验值误差低于8%，可满足工程应用，为工艺参数优化提供了依据。

工程陶瓷；脆性域；旋转超声磨削加工；切削力；数学模型

工程陶瓷因其优良的物理性能和化学性能，被加工成各种零部件（如导轨、导流罩、翼尖、控制舵等），广泛应用于航空航天、精密机械、发动机等领域。旋转超声磨削是工程陶瓷加工的主要方式，其中切削力是评价旋转超声磨削加工性能的一个重要参数。国内外对工程陶瓷旋转超声磨削加工过程中切削力研究主要采用实验手段，通过实验研究超声振动振幅、刀具转速、进给速度、加工深度等工艺参数对切削力影响规律［1-4］。但是已有学者注意到实验研究的局限性，转向采用切削力数学模型研究工艺参数与切削力关系。秦娜［5］在文献［6］材料去除率模型研究基础上，假设材料去除方式为塑性去除，根据ASPE模型，建立了钛合金旋转超声钻削加工切削力模型；清华大学冯平法等［7］根据硬脆材料脆性断裂去除机理和旋转超声加工特点，建立旋转超声恒进给率钻削硬脆材料的切削力数学预测模型；大连理工大学冯冬菊［8］根据旋转超声磨削加工过程中磨粒运动轨迹，推导了单个磨粒高频振动过程中纵向作用力计算公式。以上研究主要侧重于旋转超声钻削加工，而旋转超声平面磨削也是工程陶瓷零部件加工主要工序之一，目前其切削力模型还未见相关文献报道，本文以工程陶瓷脆性域平面加工为对象，通过建立数学模型，研究旋转超声磨削加工切削力变化机理。

1 脆性域旋转超声磨削加工过程

脆性域旋转超声磨削加工过程旋转超声磨削加工中，刀具超声振动振幅较小，只有5～20 μm。脆性域加工过程，其切削厚度远大于超声振动振幅，如图1所示。在刀具旋转和超声振动作用下，磨粒与工件表面接触处产生微观裂纹和切向划痕。

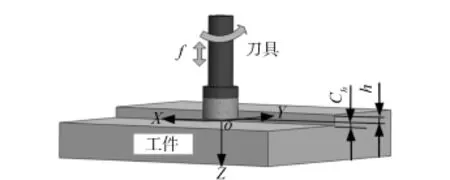
图1 脆性域加工刀具与工件接触关系Fig.1 The contact relationship between tool and workpiece in brittle machining regime

脆性域旋转超声磨削加工过程中，切削深度h大于刀具振幅A，材料主要由刀具侧面磨粒切削去除，其脆性域材料去除机理与磨削加工相同。但是，由于刀具还作纵向超声振动，刀具端面上磨粒将嵌入到已加工材料表面，当刀具振幅大于临界切深时，刀具端面磨粒嵌入到已加工表面深度增加，工件表面与刀具端面接触处应力增大，当应力达到材料断裂强度，裂纹产生并发生扩展。脆性域旋转超声加工主要特点是加工过程中材料表面也产生了微观裂纹，且工件表面由于裂纹扩展部分材料被去除。

2 切削力数学模型建立

脆性域旋转超声磨削加工过程中，分层厚度h远大于刀具超声振动振幅A，根据其加工原理，刀具与工件存在两部分接触，如图1所示。一部分是刀具端面与工件表面不断的接触和分离，另一部分是刀具侧面与工件分层侧面的接触。对刀具上单个金刚石颗粒分析，其运动轨迹为式中：R1、R2为刀具端面外圆半径和内圆半径，mm；Vf为进给速度，mm／s；A为超声振幅，mm；ω为刀具旋转角速度，rad／s；ω1为刀具振动角速度，rad／s。

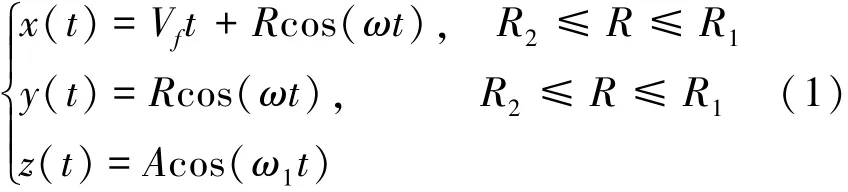
加工过程中，金刚石颗粒与工件接触，相互运动产生切削力。根据其运动轨迹，当z＞0时，刀具端面和侧面都存在金刚石颗粒与工件接触，切削力是其两部分的和。当z≤0时，刀具端面与工件分离，仅刀具侧面上金刚石颗粒与工件接触，切削力只由侧面上金刚石颗粒切削材料产生。

2.1 刀具端面切削力

脆性域旋转超声磨削加工过程中，在超声振动作用下，刀具端面上金刚石磨粒嵌入到材料内部深度δ不断变化。当δ小于临界切削深度时，材料表面产生弹塑性变形，材料去除以塑性变形为主；当δ大于临界切削深度时，材料内部产生微观裂纹，材料去除方式为脆性去除。

在刀具端面对单个金刚石颗粒切削力情况进行分析，将颗粒形状简化为Vickers锥形压头，如图2所示。当δ≤h*m时，一个尖锐锥形压头在外加载荷大小为Fbz作用下，压头压入材料内部深度与载荷存在以下关系［9-10］：

式中：ε为颗粒几何因子，对于Vickers压痕，ε≈π／2；H为陶瓷材料硬度，Pa；d为磨粒与材料表面接触对棱间距离。

图2 金刚石颗粒压痕模型Fig.2 Indentation model of diamond grit

根据图2，d与磨粒嵌入材料内深度存在关系：

式中：θ为锥形金刚石颗粒相对棱间半角。在超声振动磨削中，磨粒纵向振动，磨粒嵌入材料表面深度与超声振动作用又存在以下关系：

因此：

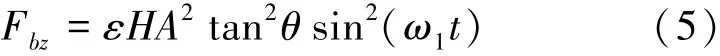
当δ＞h*m时，材料以脆性断裂去除为主。根据压痕断裂力学和工程陶瓷脆性断裂去除机理知，加工材料表面产生微观裂纹，裂纹失稳并发生扩展，工件材料内相邻裂纹相遇而去除材料。由于切削力较小，将陶瓷材料脆性去除过程中磨粒所受载荷大小约等于裂纹扩展的临界载荷，压痕断裂力学中的导致裂纹扩展的临界载荷如下式［11］：

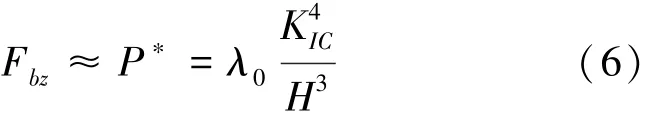
式中：KIC为工件材料断裂韧性，MPa·m1／2；λ0为与工件材料、磨粒几何形状等有关常数。

脆性域旋转超声磨削加工过程中，设超声振幅为0时，刀具端面与材料平齐，则当磨粒嵌入到材料内部深度为所需时间为

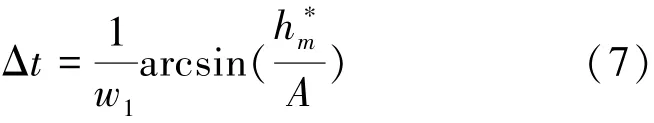
脆性域旋转超声磨削加工过程中，超声振动振幅A值大于临界切削深度h*m，对于单个磨粒在一个振动周期内，材料去除方式首先为塑性变形，然后为脆性去除。因此在一个振动周期内，单个磨粒切削力首先用式（2）表示，后用式（6）表示，其持续时间分别为2Δt和（1／（2f）－2Δt）。

在Z方向，刀具端面单个磨粒产生的平均切削力可表示为：

式中：f为刀具超声振动频率，Hz。

设刀具端面Z方向与X、Y方向上力存在与材料和磨粒有关的比例系数，则刀具端面单个磨粒产生的X方向和Y方向平均切削力可表示为

因此，在脆性域旋转超声磨削加工过程中，刀具端面上磨粒超声的切削力可表示为

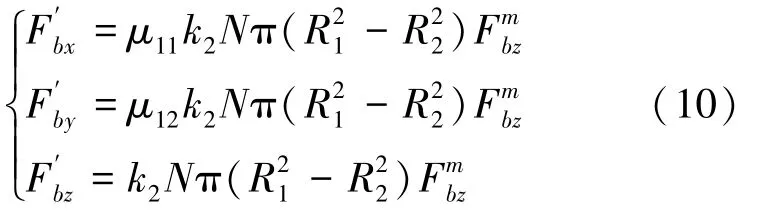
式中：k2为刀具端面单位面积有效磨粒比例，N为刀具端面单位面积磨粒数目。

2.2 刀具侧面切削力

超声振动刀具侧面加工可简化为平面磨削，如图3所示。在脆性域旋转超声磨削加工中，对于刀具侧面加工，弧段AB为接触区域，其X、Y、Z坐标矢量方向与图1中坐标相同。

在平面磨削加工过程中，刀具除旋转运动外，还存在进给运动，因此磨粒运动轨迹并不为圆弧，磨粒切削深度不断由小变大，如图4所示。l1为在Δt时间内刀具在进给运动方向上位移量，磨粒实际切削弧长为lc，最大切削厚度可表示为［12－14］

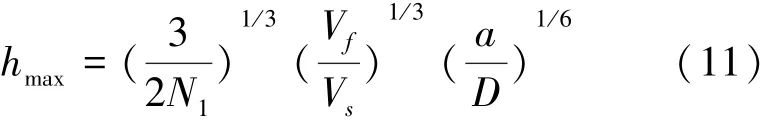
式中：N1为单位体积内磨粒数；Vf为进给速度，mm／s；Vs为刀具线速度，mm／s；a为切削深度，mm。根据图2，平面磨削切削深度相当于旋转超声磨削加工宽度b，因此a＝b；D为刀具直径，mm，D＝2R1。

图3 刀具侧面加工示意图Fig.3 The schematic diagram of side machining

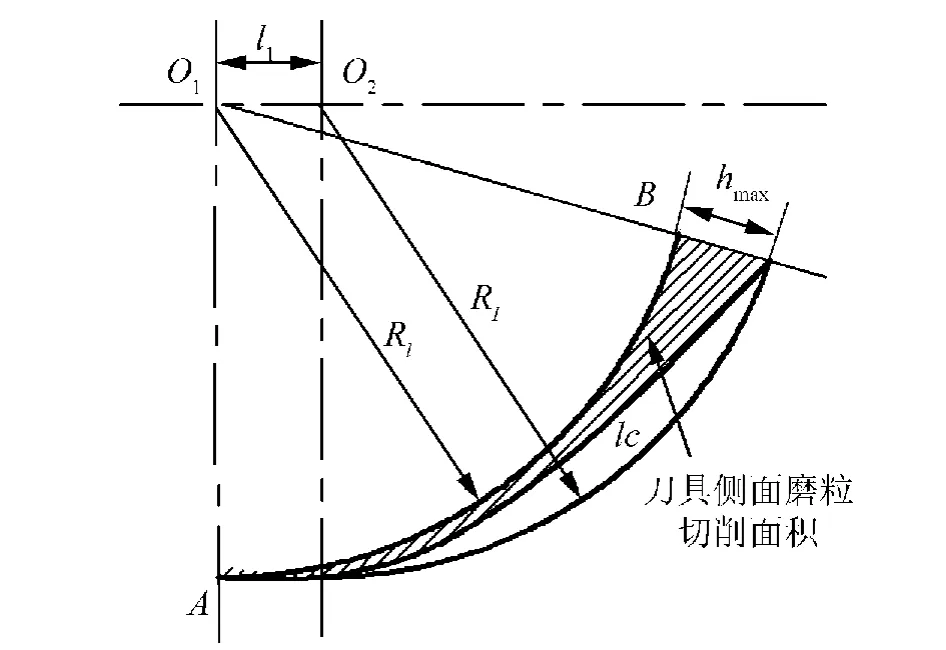
图4 磨粒切削深度变化Fig.4 The cutting depth change of grit

由于磨粒切削深度h1不断变化，因此加工过程中存在2种材料去除。当时，材料表面产生弹塑性变形，材料去除为塑性变形为主；当时，材料内部产生微观裂纹，材料去除方式为脆性去除。且切削深度与加工弧长间关系可表示为［12］

由旋转超声磨削加工特点知，刀具侧面磨粒除在图4中xo1y平面运动外，在z方向也进行纵向超声振动，根据式（1），侧面加工弧长lc可表示为

式中：tr表示刀具转动角度为φ所需时间。

根据式（2），单个磨粒在侧面加工产生的法向切削力和切向切削力为

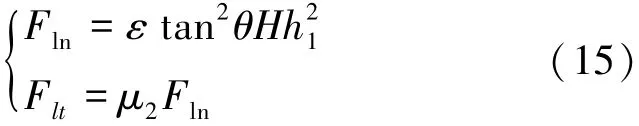
式中：μ2磨粒与材料之间摩擦系数，可近似表示为π／4tan θ［15］。

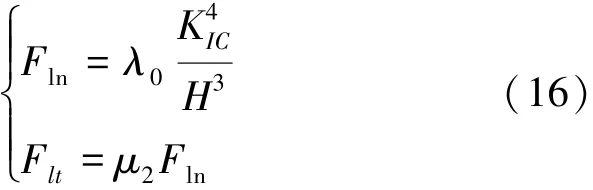
由于只有切向切削力做功，单个磨粒旋转一周做功可表示为：

图2直角坐标系内，单个磨粒做的功可表示为：

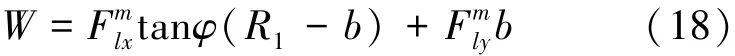
刀具纵向振动，在Z方向上单个磨粒产生的切削力可认为单个磨粒在X和Y方向产生切削力矢量和再乘以一个与材料和磨粒形状有关的比例系数μ3。刀具侧面上单个磨粒在三维直角坐标系内产生的切削力为

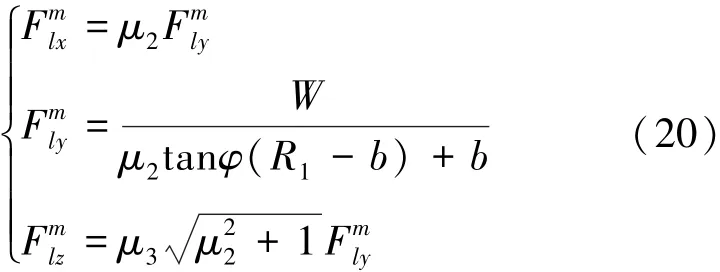
在侧面加工过程中，总切削力为刀具与材料接触面积内有效磨粒切削力之和。因此，在脆性域旋转超声磨削加工过程中，刀具侧面所有磨粒超声的切削力可表示为

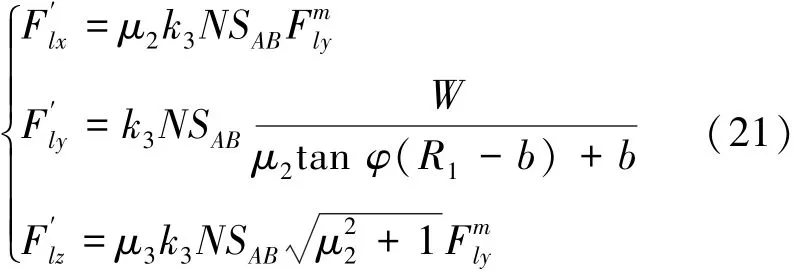
式中：k3为刀具侧面单位面积有效磨粒比例；N为刀具侧面单位面积磨粒数目；SAB为刀具侧面与材料接触面积，表示为，且h为脆性域旋转超声磨削加工深度，mm；S为刀具转速，r／min。

通过以上分析，脆性域旋转超声磨削加工切削力在X、Y、Z坐标方向可由式（10）和式（21）叠加，总切削力可表示为：

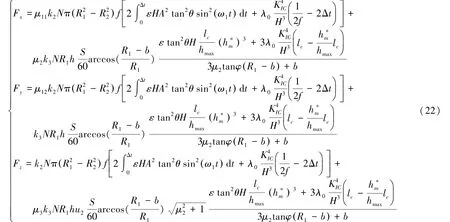
3 切削力模型实验验证

为了对脆性域旋转超声磨削加工切削力模型进行验证，通过实验研究脆性域旋转超声磨削加工过程中切削力变化。由于X、Y方向切削力与Z轴方向切削力存在比例系数，因此只对Z轴方向切削力进行分析。通过式（22），Z轴方向切削力计算公式存在系数k2、λ0、k3和μ3，这些系数可以通过实验求得，然后代入参数将理论计算值与实验结果进行对比，即可验证切削力理论模型。

3.1 实验设计

脆性域旋转超声磨削加工实验，采用的机床为DMG Ultrasonic 20 line，选用的超声振动刀具为DMG SAUER公司生产的外径为 10 mm青铜基（86%Cu、14%Sn）柱形刀具，其具体参数为：粒度D126（磨粒大小约为126 μm），浓度100（磨粒含量4.4 ct／cm3、单位面积磨粒数约为 32［16］），内径8 mm，振动频率27 500 Hz，刀具超声振幅8 μm。实验所采用的工件材料为致密度85%Si3N4陶瓷，材料的机械参数如表1所示。对加工过程中产生的切削力采用Kistler 9257B动态测力仪和Kistler 5 080 A电荷放大器进行采集，如图5所示。

表1 Si3N4陶瓷材料机械参数Table 1 The mechanical properties of Si3N4ceramics material

图5 实验设备Fig.5 Experimental equipment

为了求得式（22）中系数 k2、λ0、k3和 μ3，至少需要4个方程才可求出，但是由于k3和μ3具有乘积关系，可以将k3μ3作为一个未知数。同时为了消除实验误差，将求出多组k2、λ0和k3μ3值。加工宽度不同，k2值也将发生变化，因此只对加工宽度为5 mm时进行实验研究。本实验采用三因素两水平全因素实验设计，实验因素如表2所示，3个因素分别对应低水平值和高水平值。

参数 低水平 高水平转速／（k r · m i n－1） 6 8进给速度／（m m · m i n－1） 4 0 0 6 0 0加工深度／m m 0.1 0.1 5

由于每个参数有2个水平，共3个参数，因此实验共有8种配对，为了减少实验误差，每组实验Z轴方向切削力取3组数据，并求平均值。

3.2 实验结果与分析

通过对实验顺序排列和实验数据采集，实验结果如表3所示。

将实验顺序1、5和6组成方程组A，将实验顺序2、7和8组成方程组B，分别求得k2、λ0和k3μ3值如表4所示，两个方程组求得的k2、λ0和k3μ3相对标准偏差值分别为8.8%、10.6%和10.6%，可采用其平均值代替k2、λ0和k3μ3值。

为了验证切削力模型合理性，将表4中求出的数值平均处理，以及将实验顺序3和实验顺序4的工艺参数，代入式（22）求Z轴方向切削力值，并与实验值进行比较。计算值与实验值比较如表5所示。从表5可以看出，2组理论计算结果误差低于8%，在工程应用中，模型误差在可接受范围内。

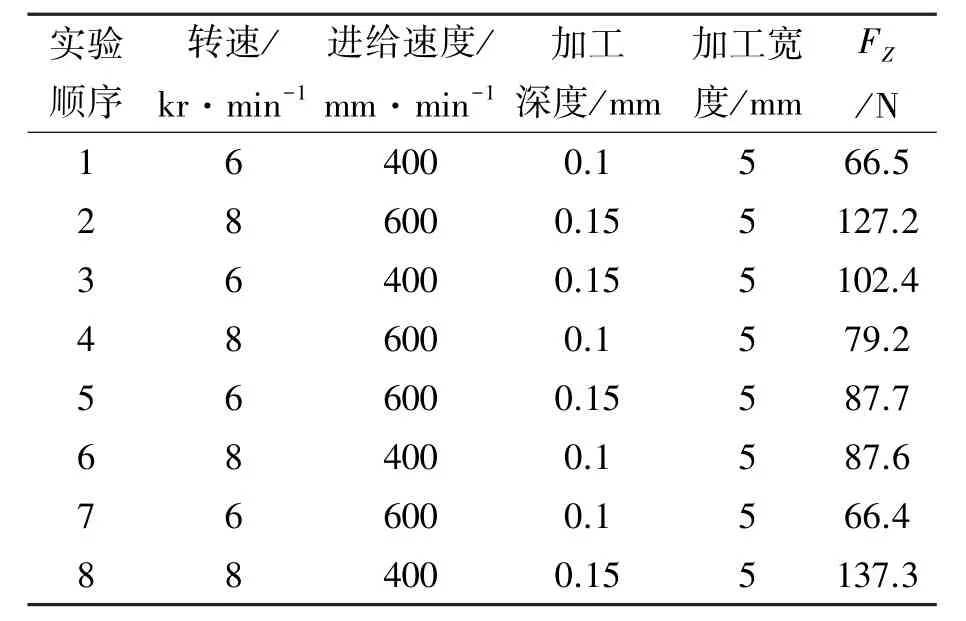
表3 脆性域加工切削力实验结果Table 3 Experimental results of cutting force in the regime brittle

表4 k2、λ0和k3μ3计算值Table 4 The calculated values of k2，λ0and k3μ3

表5 切削力计算值与实验值比较Table 5 Compare calculated values with experimental values of cutting force

通过对式（10）分析，在脆性域旋转超声磨削加工过程中，端面切削力与材料硬度、振幅、频率、磨粒角度、材料断裂韧性等参数相关；而根据式（21）分析，侧面切削力除以上参数外，还与进给速度、切削深度、转速等相关。试验中不同加工参数下端面切削力和侧面切削力如图6所示，可以看出进给速度、切削深度、转速对侧面切削力具有较大影响，最差加工参数下（第8组）切削力约为最优参数（第7组）下的2倍；而对端面切削力影响很小，不同加工参数下端面切削力值几乎未变。且脆性域旋转超声磨削加工过程中，侧面切削力是端面切削力的3～7倍。

图6 不同试验参数下切削力值Fig.6 The cutting forces of different experimentaly parameters

4 结论

1）建立了脆性域旋转超声磨削加工过程中切削力数学模型。通过全因素实验，得出理论计算结果与实验结果相比误差低于8%，证明所建立的数学模型可满足工程应用。

2）采用弹塑性力学和动量定理，建立了刀具端面切削力数学模型。端面切削力主要与振频、振幅、材料参数等有关；当进给速度、切削深度、转速变化时，其值变化量小于1 N。

3）将侧面加工简化成平面加工，根据动能定理建立了刀具侧面切削力数学模型。侧面切削力随进给速度、转速和切削深度值变化而发生较大波动，且是端面切削力的3～7倍。

［1］JIAO Y，LIU W J，PEI Z J，et al.Study on edge chipping in rotary ultrasonic machining of ceramics：an integration of designed experiments and finite element method analysis［J］.Journal of Manufacturing Science and Engineering，2005，127（4）：752-758.

［2］LI Z C，JIAO Y，DEINES T W，et al.Rotary ultrasonic machining of ceramic matrix composites：feasibility study and designed experiments［J］.International Journal of Machine Tools and Manufacture，2005，45（12／13）：1402-1411.

［3］张洪丽，张建华.切向超声振动辅助磨削对单颗粒切削力的影响［J］.兵工学报，2011，32（4）：487-492.

ZHANG Hongli，ZHANG Jianhua.Effects of tangential ultrasonic vibration on grinding force of single abrasive Grit［J］.Acta Armamentarii，2011，32（4）：487-492.

［4］卢泽生，杨亮.精密超声振动切削频率对切削力影响规律的研究与仿真［J］.航空精密制造技术，2006，42（5）：10-14.

LU Zesheng，YANG Liang.Theoretical analysis and simulation of the effect of frequency on cutting force in precision vibration machining［J］.Aviation Precision Manufacturing Technology，2006，42（5）：10-14.

［5］秦娜.旋转超声波磨削制孔的切削力建模与试验研究［D］.大连：大连理工大学，2011：32-55.

QIN Na.Cutting force model and experimental study on core drilling by ultrasonic-vibration-assisted grinding［D］.Dalian：Dalian University of Technology，2011：32-55.

［6］QIN N，PEI Z J，TREADWELL C，et al.Physics-based predictive cutting force model in ultrasonic-vibration-assisted grinding for titanium drilling［J］.Journal of Manufacturing Science and Engineering， 2009， 131（4）： 0410111-0410119.

［7］张承龙，冯平法，吴志军，等.旋转超声钻削的切削力数学模型及试验研究［J］.机械工程学报，2011，47（15）：149-155.

ZHANG Chenglong，FENG Pingfa，WU Zhijun，et al.Mathematical modeling and experimental research for cutting force in rotary ultrasonic drilling［J］.Journal of Mechanical Engineering，2011，47（15）：149-155.

［8］冯冬菊.超声波铣削加工原理及相关技术研究［D］.大连：大连理工大学，2006：36-45.

FENG Dongju.Study on the principle and relevant technology of ultrasonic milling［D］.Dalian：Dalian University of Technology，2006：36-45.

［9］任进心，康仁科，史兴宽.难加工材料的磨削［M］.北京：国防工业出版社，1999：443-452.

［10］ZHANG W，SUBHASH G.An elastic-plastic-crack model for finite element analysis of indention cracking in brittle materials［J］.International Journal of Solids and Structures，2001，38（34／35）：5893-5913.

［11］龚江宏.陶瓷材料断裂力学［M］.北京：清华大学出版社，2001：23-51.

［12］谢桂芝，尚振涛，盛晓敏，等.工程陶瓷高速深磨磨削力模型的研究［J］.机械工程学报，2011，47（11）：169-176.XIE Guizhi，SHANG Zhentao，SHENG Xiaomin，et al.

Grinding force modeling for high-speed deep grinding of engineering ceramics［J］.Journal of Mechanical Engineering，2011，47（11）：169-176.

［13］AHN Y，FARRIS T N，CHANDRASEKAR S.Sliding micro-indentation fracture of brittle materials：role of elastic stress fields［J］.Mechanics of Materials，1998，29（3／4）：143-152.

［14］谢桂芝，黄含，盛晓敏，等.工程陶瓷高效深磨磨削力和损伤的研究［J］.湖南大学学报，2008，35（5）：26-30.

XIE Guizhi，HUANG Han，SHENG Xiaomin，et al.Investigation on the grinding gorce and the ground damages in the high efficiency deep grinding of advanced ceramics［J］.Journal of Hunan University，2008，35（5）：26-30.

［15］任敬心，华定安.磨削原理［M］.北京：电子工业出版社，2011：356-366.

［16］孟丹.电镀金属结合剂砂轮磨粒特征的检测［J］.装备制造技术，2009，8：9-10.

MENG Dan.Metal plating abrasive wheel binder concentration detection［J］.Equipment Manufacturing Technology，2009，8：9-10.

（责任编辑：陈峰）

Investigation of the cutting force of rotary ultrasonic grinding machining in the brittle regime for engineering ceramics

WEI Shiliang1，ZHAO Hong1，XUE Kai1，JING Juntao1，2
（1.School of Mechanical and Electrical Engineering，Harbin Engineering University，Harbin 150001，China；2.China Aerospace Science＆Industry Corp Harbin Fenghua CO.Ltd，Harbin 154001，China）

The theoretical investigation of the cutting force of rotary ultrasonic grinding machining（RUGM）for engineering ceramics in a brittle regime was conducted for the purpose of solving the limitations of the experimental results due to the limited range of process parameters and the number of experiments.Based on the mechanism of RUGM，the formula of the cutting force caused by the bottom and side machining of a single diamond in the brittle regime was deduced by the theorem of linear momentum and kinetic energy，and was combined with the indentation fracture mechanics and elastic-plastic mechanics.Meanwhile，the mathematical model of the cutting force for RUGM in the brittle regime was established.Finally，the model was verified by the experiments.The results show that the error rate of the cutting force model between the calculation value and the experimental value is less than 8%.As a result，it can meet the demands of engineering applications.So it provides the foundation for process parameters optimization.

engineering ceramic；brittle regime；rotary ultrasonic grinding machining（RUGM）；cutting force；mathematical model

10.3969／j.issn.1006-7043.201306030

TH16

A

1006-7043（2014）08-0976-06

http：／／www.cnki.net／kcms／doi／10.3969／j.issn.1006-7043.201306030.html

2013-06-07. 网络出版时间：2014-06-27 16：18：39.

“十二五”航天支撑技术预研基金资助项目（61801060103）；黑龙江省自然科学基金重点资助项目（ZD201313）.

魏士亮（1987-），男，博士研究生；赵鸿（1961-），男，教授，博士生导师.

赵鸿，E-mail：zhaohong_heu＠163.com.