分块GPCA和多视点图像融合

吴远昌，孙季丰，李万益

（华南理工大学电子与信息学院，广东 广州510641）

分块GPCA和多视点图像融合

吴远昌，孙季丰，李万益

（华南理工大学电子与信息学院，广东 广州510641）

为了实现对多视点图像的融合，提出了一种使用分块广义PCA（GPCA）的方法。分块可以将图像处理的过程细化，简化计算GPCA则考虑了二维数据的空间关联性，用于灰度图像降维时有较好的效果，两者的结合是文章的一个创新。由于需要考虑常规多视点图像的不同视点间存在位移差的事实，图像的预处理环节加入了必要的配准和投影变换操作。因此，整个方法主要包括图像匹配、投影变换、分块GPCA计算和融合等环节。为验证方法的可行性和准确性，文章引入了二维经验模态分解BEMD。结果表明，和BEMD相比，所提方法在图像融合的性能和计算复杂度上都表现出了优势，有一定的实用价值。

多视点图像融合；广义PCA；分块；图像配准；二维经验模态分解

传统的图像融合分为像素级融合、特征级融合和决策级融合，它们过于注重图像被处理的层次，但忽略了方法本身所具有的特点。实际应用中，为了描述和研究方便，人们更倾向于从对图像融合处理的手段上来命名各种方法。因此，研究者们分别提出了基于小波变换，金字塔分解，HIS空间，形态学，统计学，神经网络，PCA等的图像融合［1］。此外，也有人提出了一些被应用得相对较少，但效果比较理想的方法，如混合像元分解法［2］、多波长的数字全息技术法［3］、梯度法［4］以及模糊技术法［5］等。另外，多视点图像以其独特的优势，在实际应用中发挥着不可替代的优势。多视点图像的存储，运输是困扰人们的一个难题。因此，实现对多视点图像的融合压缩具有十分重要的实际意义。由于多视点图像所具有的高分辨率、高信息量特点，为了后续计算处理的方便，预先对图像进行降维也是研究的重点。同时，在融合压缩的时候，由于不同图像间存在位移和角度的变换，所以需要对图像进行配准之后再根据具体情况进行处理。文章尝试以GPCA为基础，结合图像的变换配准技术，对多视点图像进行融合处理。

1 多视点图像及其融合技术

{1，2，...，r}，j∈{1，2，...，c} 的像素值I( i，j)都是属于该集合的一个元素，即I＝{I( i，j)｜1≤i≤r，1≤j≤c} 。当图像非常大

现实生活中，对于某一场景，可以从不同的时刻或角度得到关于它的一组观测图像，这些图像的整体就叫做多视点图像。人们借助多视点图像技术来实现对目标的跟踪，人脸的识别，手势的估计，以及多用户的交流。

在多视点图像的基础上发展起来的多视点视频能够更好地将实际的场景呈现在观察者面前，更具有真实感。但是，随着相机数目的增加，多视点视频的数据量也成倍地增加，这给视频数据的存储和传输带来了极大的困难。因此，实现对多视点视频的高效压缩成为了人们必须要解决的难题。

目前，对多视点视频的压缩主要以去冗余为中心，但从人眼的观察方式来说，以融合为中心的压缩更接近人的视觉特性。由于多视点视频和多视点图像之间的派生关系，对多视点视频的融合归根到底还是对多视点图像的融合。进行多视点图像融合，需要将原始各视点图像中所包含的信息尽量完整地整合到一幅新的图像中去。这样，人们才能借助新生成的图像，对原场景有更形象、直观地了解。

从集合的角度来看，如果把大小为rc的图像I看作一个有限数据集，那么每个像素点 i，j( )，i∈时，集合I所包含的数据点也就比较多。当将I的每一个元素都看作属于它的一个一维统计特征时，I的维数必然会很高。

实践表明，对特征维数很大的图像集I直接用传统的方法进行融合，虽然可能得到比较好的效果，但计算复杂度一般都比较高，这对于一些追求高效率的应用程序来说是不可取的。所以，在进行融合处理之前，最好在保证原有大尺寸、高分辨率图像的主要信息不丢失的前提下，对图像进行降维。被处理的图像，由于数据点减少会给后续的运算处理带来极大的方便。

2 灰度图像的分块GPCA方法

PCA是一种传统的流形学习方法，它通过从样本数据中提取主要特征来达到减少计算量的目的。假设存在K幅图像的样本集，每幅图像Ik（k＝1，2，...，K）大小都为r×c。首先，把Ik的所有像素点按行重新排列成一个行向量sk，sk的大小为1×N，其中N＝r×c；然后，所有的sk组成一个新的矩阵A＝ [s1s2...sK]T；再对A进行奇异值分解，求取A最大的d个特征值所对应的特征向量α；最后，用向量的投影变换将每一个sk进行投影，便得到了原图像的d维表述。这就是灰度图像的PCA方法。

GPCA是PCA的改进，相比于PCA以一维列向量为出发点，GPCA对数据的处理是基于二维矩阵的。由于这种不同，GPCA在很大程度上能保留数据间的空间关联性。图1描述了在对灰度图像进行处理时，GPCA和PCA原理上的区别［6］。

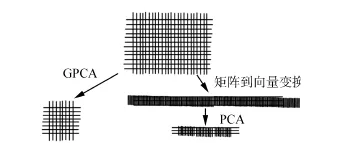
图1 PCA和GPCA的区别Fig.1 Difference of PCA and GPCA

理论上，可以用GPCA代替PCA对所有的灰度图像进行处理。但是，由于一般的图像尺寸都比较大，直接进行矩阵运算，计算量比较大。实践证明，将大尺寸的图像分割成独立的小块后再运用GPCA，虽然表面上计算的次数增加了，但总的计算复杂度是下降的。这样，既保留了原始方法的精确度，又在很大程度上降低计算的复杂度。因此，本文在文献［6］的基础上，提出了基于分块的GPCA方法。

对于原始的图像A，先将它分成n个大小相同的子块，并用Ai，i∈(1，2，...，n )来表示第i个子块，则基于分块GPCA方法的步骤如下：

1）计算图像样本集合A1，A2，...，An的均值

3）令LO← Ed，O( )T，其中Ed是d×d的单位矩阵，d是图像期望降到的维数，O是零矩阵；

4）令k＝0，初始化图像经过GPCA反变换回去时的均方根误差REMS k()←∞；

6）令 k ＝ k ＋ 1，同时进行赋值 Rk←

9）计算REMS k()＝

10）如果REMS k－1( )－REMS k()≤η，那么转11），否则，跳转到5）继续执行，其中η是预先设定的一个阈值；

11）对变换矩阵Lr×d和Rc×d分别赋值，即L←Lk，R←Rk；

12）对于每一个i∈ { 1，2，...，n}，由公式Di＝计算原始灰度图像经过变换后的灰度投影并返回。

3 图像的配准

一般的多视点图像在像素点上存在各种各样的变换关系，有平移、缩放和角度变换等，图像的配准就是求取这些不确定变换关系的过程。假设有两幅相邻的视点图像Image 1和Image 2，那么Image1中任意一点（x1，y1）到Image2中对应点（x2，y2）的变换关系可用下面的变换公式来描述［7］：

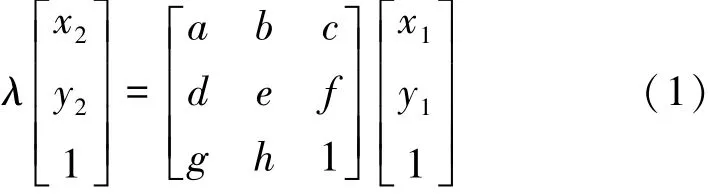
式中：λ是变换尺度，a～h是相关的变换系数。单应矩阵H定义为

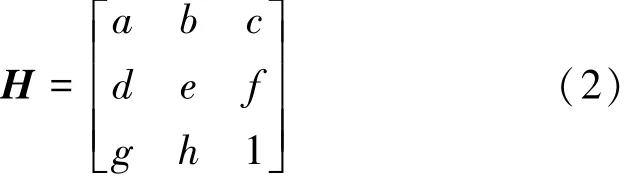
由式（2）可知：

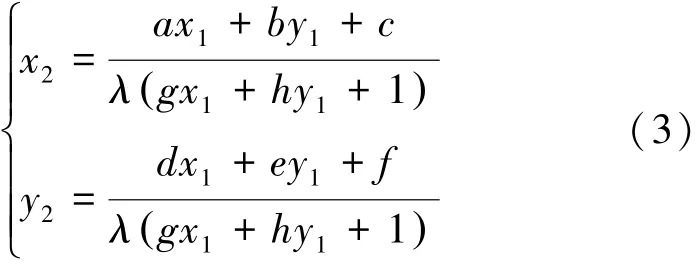
为处理方便，在尺度变换不变的情况下，只考虑像素点间的水平和垂直移位。则可以得到a＝e＝1，λ ＝1，b＝d＝g＝h＝0，同时有

式中：c和f分别代表像素点的水平和垂直移位。

在图像配准中，上述过程称为图像的粗配准。粗配准只考虑了像素点间的平移问题，这样一方面可以简化计算的复杂度，另一方面也使得图像的边信息（对于大小为m×n的图像Image 1和Image 2，边信息就是Image 2相对于Image 1的水平和垂直位移）比较容易描述。当用I1来代表Image 1，I2代表Image 2时，可以计算出它们大 致 的 重 叠 区 域 为 I1(1∶（m－f），1∶（n－c）)和I2(（1＋f）∶m，（1＋c）∶n)。在文中，将参照 Rilling［8］等人所提出的方法对分块降维后的图像进行配准。

4 图像的融合

完成图像降维和配准之后，还需要对来自不同视点的图像进行融合。由于在图像融合的3个层次中，基于像素点的融合最普通，应用也最广泛，所以常规研究中多利用像素点的基本特性进行融合。文章在对配准后的图像进行融合时，对于不同的区域，采用了不同的处理方法，如图2所示。

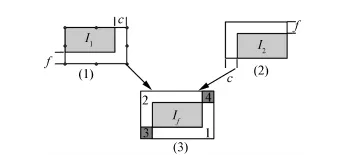
图2 图像融合示意图Fig.2 Schematic of image fusion

图2 中，I1表示视点1的图像，I2表示视点2的图像。其中I1和I2大小相等，均为m ×n，I1、I2中的灰色部分表示两幅图像的重叠区。在前面的配准中，由于I1水平和垂直方向上分别平移c和f才得到I2，所以重叠区的大小为 m －f( )× n－c( )。进一步地，由I1、I2的对应关系，可以计算融合后的新图像If。其中If的大小为 m ＋f( )× n＋c( )，它几乎完全保留了I1、I2的信息。

为了描述方便，将If分成5个区域，它们分别是中间的灰色区域和边上的1、2、3、4这4个区域。由前后变换的关系可知，1属于I1中除去重叠区后剩下的部分，2属于I2中除去重叠区后剩下的部分，3和4是新生成的部分，而灰色部分是I1、I2的重叠区。由于1和2分别是I1和I2所特有的部分，在新的图像中，直接保留。对于3、4两个部分，因为它们在外围的两个边界上和1、2相邻，为了使融合图像的像素点在边界处过渡平稳，用一个3×3的算子S从它们的交界处开始进行加权插值，其中

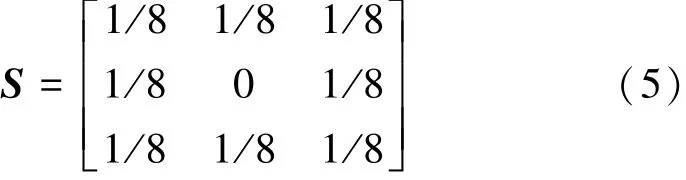
需要注意的是，在对区域3、4进行插值时，像素点的索引方向是不同的。对于3，规定索引的正方向为从右到左，从上到下；而对于4，索引的正方向为从左到右，从下到上。对于灰度重叠区的处理，则显得比较麻烦些。另外，虽然I1和I2中的灰色区域表现的场景是相同的，但由于拍摄视点的不同，它们表现出来的明亮程度和颜色信息还是有些不同。所以，不能将两部分的像素值进行简单加和之后再平均。为了提高融合质量，可以采用小波融合的思想［9-10］。

用小波变换的思想对重叠区进行融合时，首先要对图像进行N层小波分解，得到 3N＋1( )个不同频带，这些频带包括3N个高频子图像和1个低频子图像。在融合的时候，对于高频部分，直接取两幅源图像中相应的小波分解系数绝对值最大者的值作为融合图像的分解系数，对于低频部分，处理的规则相对复杂一些，具体步骤如下：

1）假设C I()表示图像I的小波低频成分的系数矩阵，p＝ m，n( )表示小波系数的空间位置，那么C I，p( )就表示小波低频成分系数矩阵下标为m，n( )的元素的值；

2）以p为中心选定一个小区域Q，u I，p( )表示C I()以 p为中心，在 Q内的均值，G I，p( )为C I()在Q内的区域方差显著性，满足

式中：w q()为权值，离p越远，值越小；

3）按照式（6）分别计算I1、I2的区域方差显著性G I1，p( )、G I2，p( )，然后计算它们在p点的区域方差匹配度：

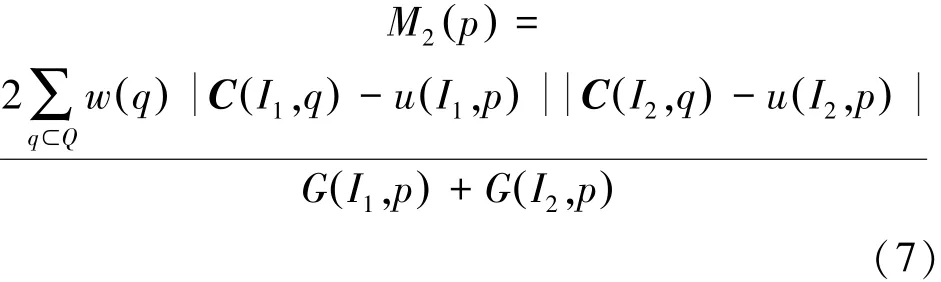
4）设定一个匹配度阈值T，当M2p()＜T时，融合策略为

当M2p()≥T时，融合策略为平均策略

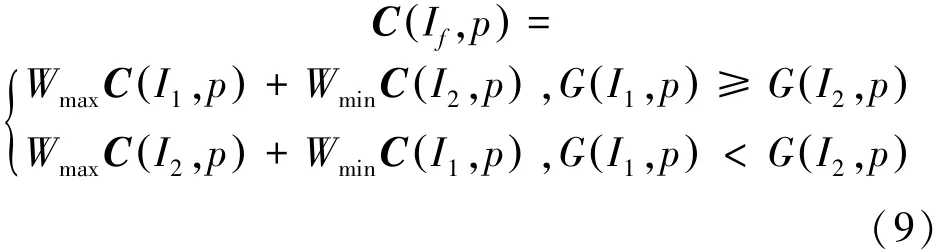
其中，

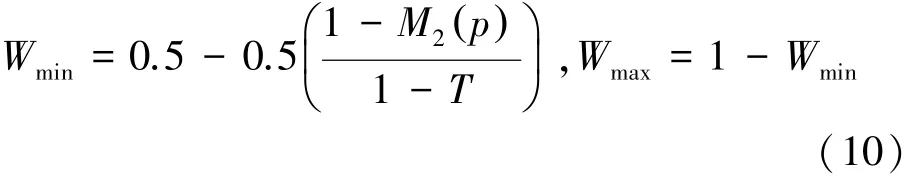
上述处理完成后，再进行小波重构，便可以得到理想的基于小波变换的融合图像。

5 实验结果分析

文章采用2组大小为480×640的灰度图像flamenco 1和flamenco 2作为实验图像，下面是对整个融合过程中各个环节的实验结果进行的简要分析。

5.1 分块GPCA法

正如前面所说，如果将单幅图像直接进行运用GPCA方法，由于图像包含的总像素数为307 200个，如此庞大的数据会耗费大量的时间。因此，需要将原始图像I1、I2平均分块后再降维。文中I1、I2均被分为9块，每一块的大小为240×320。以I1为例，设9块的编号分别为1～9，首先选取1的区域为I1（1∶240，1∶320），接着将2所属区域设定为I1（1∶240，161∶480），3设为I1（1∶240，321∶480），从这里可以看出，2和1、3是存在重叠区域的。接下来用同样的方法设定4～6的区域，不过要注意4和1、7有重叠，5和2、4、6、8有重叠，8和5、7、9有重叠。这样设定之后，每一块的大小都为原始图像的1／4。

分析发现，在不进行分块的条件下，GPCA的复杂度在最优的情况下为

O knd r＋c( )2＋r3＋c3＋ncd r＋d( )

( )（11）式中：k是迭代计算次数，n是样本数，d是所得低维空间维数，r、c分别是图像的长和宽。相应地，如果把每个样本分成N×N块，那么计算的复杂度为

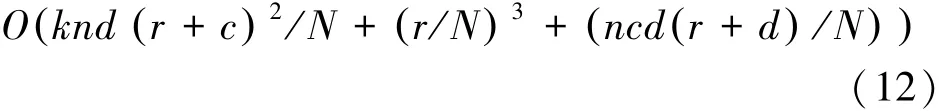
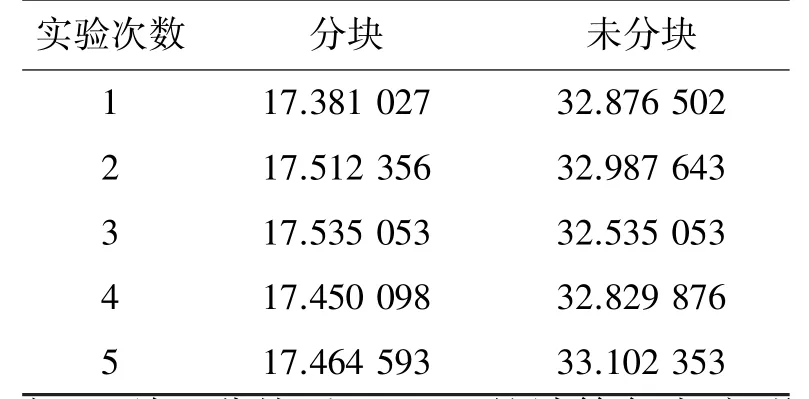
表1 分块和未分块所花时间Table 1 Time with blocking and non-blocking s

由上可知，分块后，GPCA的计算复杂度明显降低。表1是每一次实验中对图像分块和不分块时所需要的具体时间。

由表1可知，将图像先分块、再降维所需的时间比不分块直接进行处理少得多。因此，在实验中采用的是将图像分块处理的方法。

5.2 融合结果分析

图3中（a）和（b）是原始的两幅灰度图像 I1、I2；（c）、（d）中从左到右、从上到下依次排列的9幅图像是I1、I2的9个分块子图像维度降至20的情景；图3（e）中左边和中间的图像分别由（c）、（d）中的子块融合的得到，右边的图像则是前两部分由本文所述方法进行融合所得的结果；（f）是由（e）中第3部分的结果经GPCA重构后得到的最终图形。

图3 图像的降维及重构Fig.3 Dimension reduction and reconstruction of image

由上面（c）、（d）可知，两幅图像经降维处理后，依然存在一定的关联性，这可由它们像素点矩阵所表现出的相似性看出来。但由于降维后，原始图像的信息丢失了一部分，这种关联性表现得并不是特别明显。另外，因为降维后的图像块重组采用的是简单的加和，因此（e）中的左边和中间图像可以看到在邻接处存在相对明显的过渡带，这是后续工作需要解决的问题之一。

图像融合中，对最终结果进行质量评价也是一个必不可少的环节。现阶段，已知的质量评价方法有2种：基于参照图像和不采用参照图像。其中，基于参照图像的方法，主要考虑的是融合输出图像F和参照图像R之间的参数相似性，它包括均方误差、平均绝对误差、互信息、相关系数等［11］。不用参照图像的评价方法选择的参数更具多样性，Xydeas的边信息之和，Qu.G的平均互信息，Wang的结构相似性和Hossny所提出的方案都是其中之一［12］。为了计算方便，文章选择了标准差和信息熵这2个参数。为了说明文中所述方法的可行性，将实验结果和文献［7］中基于BEMD的结果进行了对比。表2是5次实验中，用GPCA和BEMD对flamenco图像进行融合计算时得到的标准差和信息熵。

从表2可以看出，同BEMD法相比，用分块GPCA融合得到的图像虽然信息熵比较小，但是像素灰度级相对较大。在实验条件下，两者的融合效果基本接近，都满足了一般图像融合的要求。

另外，由图3中（f）和（a）、（b）的对比可以看到，用分块GPCA融合生成的图像和原始图像相比，图像的清晰度相对较低，在一些细节上（如最右边舞者的面部）也存在信息量的丢失，这是文中实验结果存在的一个不足。

表2 flamenco图像融合结果Table 2 Fusion result of flamenco images

6 结论

多视点图像比常规图像具有更多的信息，实现对多视点图像的有效处理是未来游戏和监控领域实现跨越式发展的要求。文中提出了一种基于分块GPCA降维和像素点配准的多视点图像融合方法，总体说来，它具有以下几个特点：

1）由于引入了分块和数据降维，同BEMD和单纯的小波变换等传统方法相比，方法在计算的复杂度和运行效率上有较大的优势。

2）目前，方法只局限于对灰度图像的处理。如果输入RGB彩色图，则需要预先进行转换。

3）由方法得到的融合图像性能并不特别高。

因此，在后续的工作中，提高图像的融合质量，扩大可处理图像的范围，是在使用分块GPCA时需要重点解决的两个问题。此外，将文中所述方法应用于多视点视频编码的前处理，提高编码效率，也是一个很有实践意义的课题。

［1］殷兵云.多传感器图像融合方法研究［D］.西安：西安电子科技大学，2009：7-9.

YIN Bingyun.Research of multi-sensor image fusion methods［D］.Xi＇an：Xidian University，2009：7-9.

［2］ZHUKOV B，OERTEL D，LANZL F，et al.Unmixingbased multi-sensor multi-resolution image fusion［J］.IEEE Transactions on Geoscience and Remote Sensing，1999，37（3）：1212-1226.

［3］JAVIDI B，FERRARO P，HONG S，et al.Three dimensional image fusion by use of multi-wavelength digital holography［J］.Optics Letters，2005，30（2）：144-146.

［4］PETROVIC V，XYDEAS C.Gradient-based multi-resolution image fusion［J］.IEEE Transactions on Image Processing，2004，13（2）：228-237.

［5］RANJAN R，SINGH H，MEITZLER T，et al.Video image fusion process using fuzzy technique［C］／／Defense and Security Symposium.International Society for Optics and Photonics.Kissimmee，USA，2006：1-6.

［6］VIDAL R，MA Y，SASTRY S.Generalized principal component analysis（GPCA）［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，2005，27（12）：1945-1959.

［7］孙季丰，何沛思.一种基于CEMD和融合的多视点图像编码方法［J］.电子与信息学报，2011，33（4）：1007-1011.

SUN Jifeng，HE Peisi.A multi-view image coding scheme based on fusion and CEMD［J］.Journal of Electronics and Information Technology，2011，33（4）：1007-1011.

［8］RILLING G，FLANDRIN P，GONALVES P，et al.Bivariate empirical mode decomposition［J］.Signal Processing Letters，2007，14（12）：936-939.

［9］TIAN J，CHEN L.Adaptive multi-focus image fusion using a wavelet-based statistical sharpness measure［J］.Signal Processing，2012，92（9）：2137-2146.

［10］ROY S，HOWLADER T，RAHMAN S.Image fusion technique using multivariate statistical model for wavelet coefficients［J］.Signal，Image and Video Processing，2013，7（2）：355-365.

［11］ABI-J N，KRUECKER J，KADOURY S，et al.Multimodality image fusion-guided procedures：technique，accuracy，and applications［J］.Cardiovascular and Interventional Radiology，2012，35（5）：986-998.

［12］MITCHELL H.Image fusion theories，techniques and applications［M］.Springer，2010：18-86.

（责任编辑：陈峰）

Block-based GPCA and multiview image fusion

WU Yuanchang，SUN Jifeng，LI Wanyi
（School of Electronic and Information Engineering，South China University of Technology，Guangzhou 510641，China）

In order to complete the fusion of multiview images，this paper presents a generalized block-based PCA（GPCA）method.Blocking can refine the progress of image processing and simplify the calculation.GPCA considers the spatial correlation between two-dimensional data and has better results in dimensinality reduction of gray images，so it is an innovation by combining these two methods in this article.Because there has to be recognition of the fact that there exists differential displacement between the different viewpoints of the conventional multi-view image，some necessary registration and projection transformation operations are added to the pre-processing of the images.Thus，the entire method includes image matching，projection transformation，computing of GPCA，image fusion and so on.In order to verify this method＇s feasibility，this article has introduced bi-dimensional empirical mode decomposition（BEMD）.The results show that compared with BEMD，GPCA demonstrates certain advantages in performance and computational complexity regarding image fusion，and has some practical value.

multiview image fusion；GPCA；blocking；image registration；BEMD

10.3969／j.issn.1006-7043.201306046

TP391

A

1006-7043（2014）08-1022-06

http：／／www.cnki.net／kcms／detail／23.1390.U.20140701.1534.003.html

2013-07-30. 网络出版时间：2014-07-01 15：34：48.

国家自然科学基金资助项目（61202292）.

吴远昌（1988-），男，硕士研究生；孙季丰（1962-），男，教授，博士生导师.

孙季丰，E-mail：ecjfsun＠scut.edu.cn.