谐振式微型管道机器人设计与实验

刘 磊，李 娟，李伟达，秦 佳

（苏州大学机电工程学院，江苏苏州215021）

谐振式微型管道机器人设计与实验

刘 磊，李 娟，李伟达，秦 佳

（苏州大学机电工程学院，江苏苏州215021）

针对直径在18～30 mm范围内的细小管道难以检测的问题，提出一种微型机器人。该机器人采用谐振原理驱动，简化了传动机构。由微型电机带动偏心轮旋转作为激励源，建立了机器人在管道壁约束下的数学模型，求解机器人柔性足与管壁碰撞产生的角加速度和接触点位置，分析了机器人的运动机理。研制机器人样机，并搭建管道试验环境，进行速度和牵引力测试实验。最小样机尺寸15 mm×15 mm×22 mm，由实验结果得出：样机在8 V电压下，速度最高可达到68.29 mm／s，功耗约为0.15 W，最大爬坡角度30°。

非线性振动；管道机器人；谐振驱动；结构设计

随着现代高科技机械行业的快速发展，管道的建设和利用也得到了快速发展，尤其是在发电、制冷、航空、化工等行业，细小工业管道得到了普遍使用。但发展的同时，其弊端也不断呈现，长年的介质腐蚀，机械振动以及制造缺陷的作用和影响，会导致管道产生裂纹，管壁减薄或破裂。定期检查，及时发现缺陷及其扩展情况，并采取相应的修补或堵塞措施，是管道系统安全运行的重要保证［1］。传统的管道检测方法一般采用直接目视或用一些简单的工具进行检查，存在着不安全、破损不易发现、判断不准确等诸多弊病。用机器人技术对细小管道进行检查、诊断、维护等作业成为近来人们关注的热点。哈尔滨工业大学研制了具有差动运动功能的管道机器人，该机器人在通过弯管时可根据管道环境利用三轴差动机构自动调节各驱动轮的转速，从而提高机器人通过弯管时的运动柔顺性，上海交通

大学开发了基于微型电机的肠道机器人，实现的机构本体蜷缩时尺寸为Φ13 mm×50 mm，能够实现10 mm的轴向步距与8 mm的径向变形。吉林大学陈西平等研制了一种谐振型压电式管内移动机构，在压电材料驱动下，机构发生谐振并在足端产生椭圆运动驱动机器人运动［2-7］。

传统机器人结构复杂，小型化困难，受尺度效应影响小型化后运动效率急剧下降。难以适应微型管道的作业环境。采用谐振驱动可以避免复杂的传动机构，易于小型化，同时驱动控制也较易实现。本文提出一种基于谐振驱动原理的管道机器 人，设计谐振式移动机构，介绍机器人的组成结构和运动原理。搭建相应的实验平台，对研制的样机进行实验研究。

1 建模与仿真分析

1.1 运动原理介绍

微型管道机器人结构如图1所示，主要包括有微型电机、偏心轮、弹性支架组成的激励源，节、前端盖、后端盖等结构件和覆盖外表面的柔性纤毛（柔性足）等。微型电机带动偏心轮旋转，偏心轮的离心力激励弹性支架产生振动；振动经壳体传递给柔性足；柔性足与管壁呈一定角度，在振动时其末端与管道壁发生碰撞和非对称摩擦，当激励频率与系统动力学特性匹配时，机器人在柔性足的推动下产生运动，如图2所示。

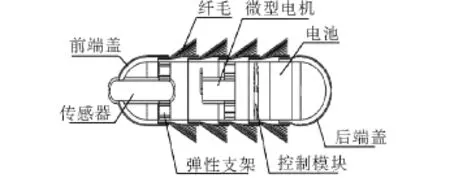
图1 微型管道机器人样机结构Fig.1 The structure of micro-pipe robot prototype

偏心轮转动到下方时，通过支撑结构将振动能量传递给单向柔性足，机器人下端柔性足和管壁接触，发生挤压，摩擦力增大；上端柔性足与管壁间压力减小，摩擦力减小，发生相对滑动。机器人本体向前移动。以此循环，由于柔性足的单向特性，柔性足与管壁在2个方向的摩擦系数不等，偏心轮旋转引起柔性足在前进方向上摩擦力发生变化，所以引起机构向前运动。当激励频率在机器人固有频率附近、柔性足与管壁间夹角适宜、增大激励电压，能实现管道机器人的最佳运动状态。

机器人在管道内运行时输出牵引力的大小和柔性足所受的正压力、柔性足与管壁之间的摩擦因数有关。单向柔性足前后运动摩擦因数不同，电机旋转时，上下两端柔性足所受摩擦力相对改变，两端摩擦力差值越大，机器人输出牵引力越大。此外，当机器人遇到障碍或管道直径微小变化时能够实现一定程度的柔性调节。

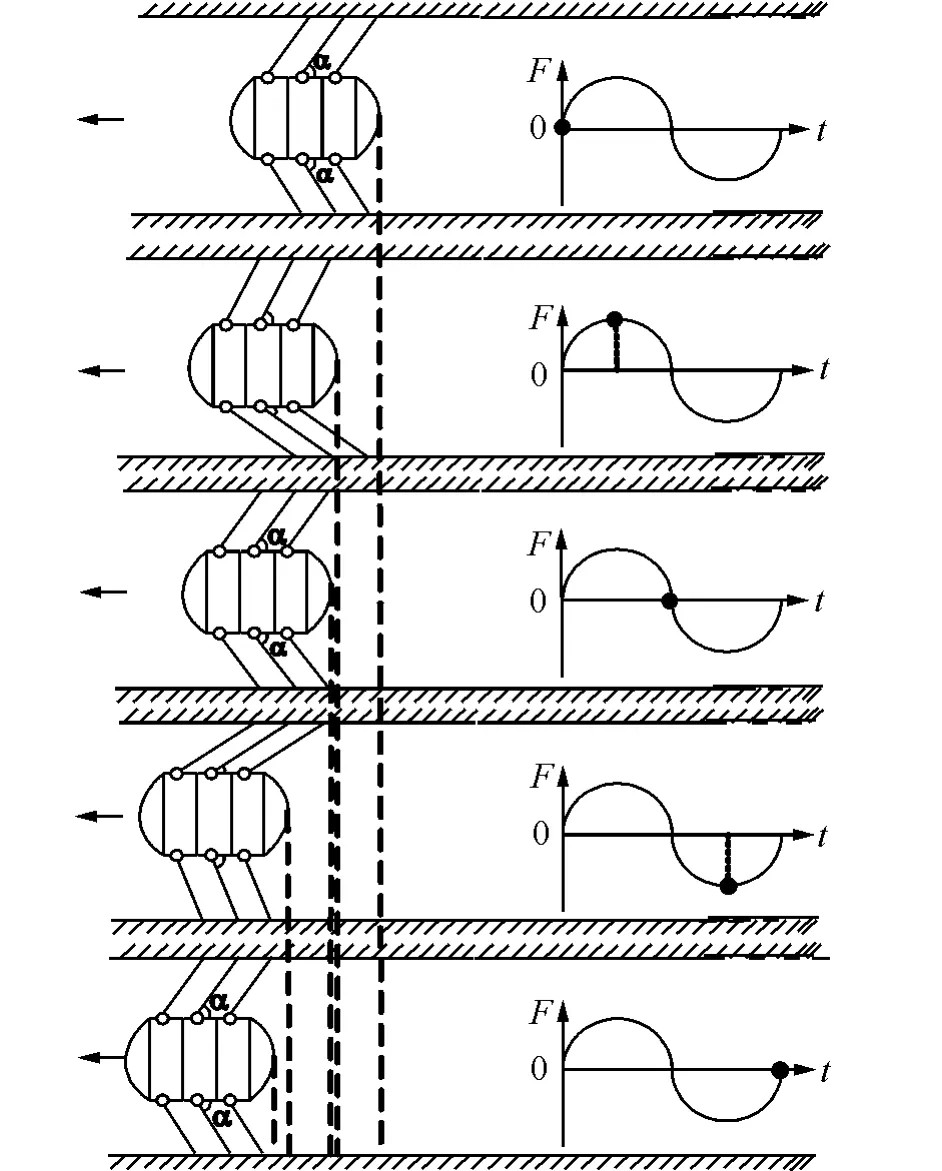
图2 机器人运动原理Fig.2 Theory of robot motion

1.2 柔性足的动力学模型

机器人物理模型图3所示，截取机器人的一个环节，将机器人基体简化为质量为m0的单一几何体，取一对柔性足进行受力分析，柔性足和简化基体的夹角为α，激励源采用幅值为F0，频率为f的正弦激励。

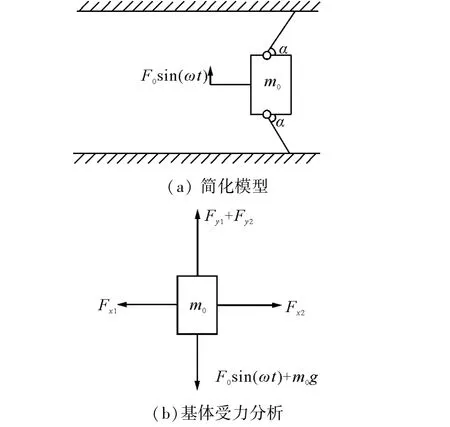
图3 机器人物理模型Fig.3 Physical model of the robot

离心力F0由微型电机带动偏心轮旋转产生，其方向背离旋转轴心，在剖视图中，离心力在y方向的投影为F0sin（ωt）。

简化动力学模型如图4所示，取O点为坐标原点，建立直角坐标系 Oxy。在 Oxy中，基体坐标A（x0，y0），上下柔性足端坐标分别为 B（x1、y1）和C（x2、y2），α为柔性足与管壁所成夹角，θi（i＝1，2）为柔性足的角位移，柔性足长L，根据几何关系，可得xi、yi方程：

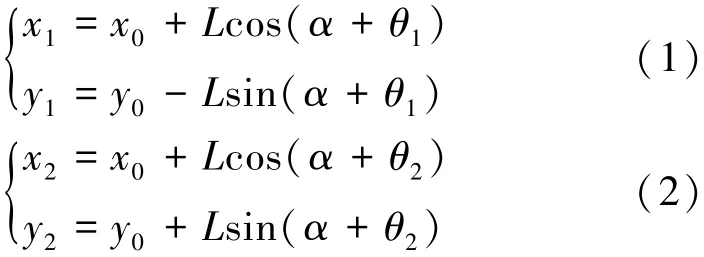
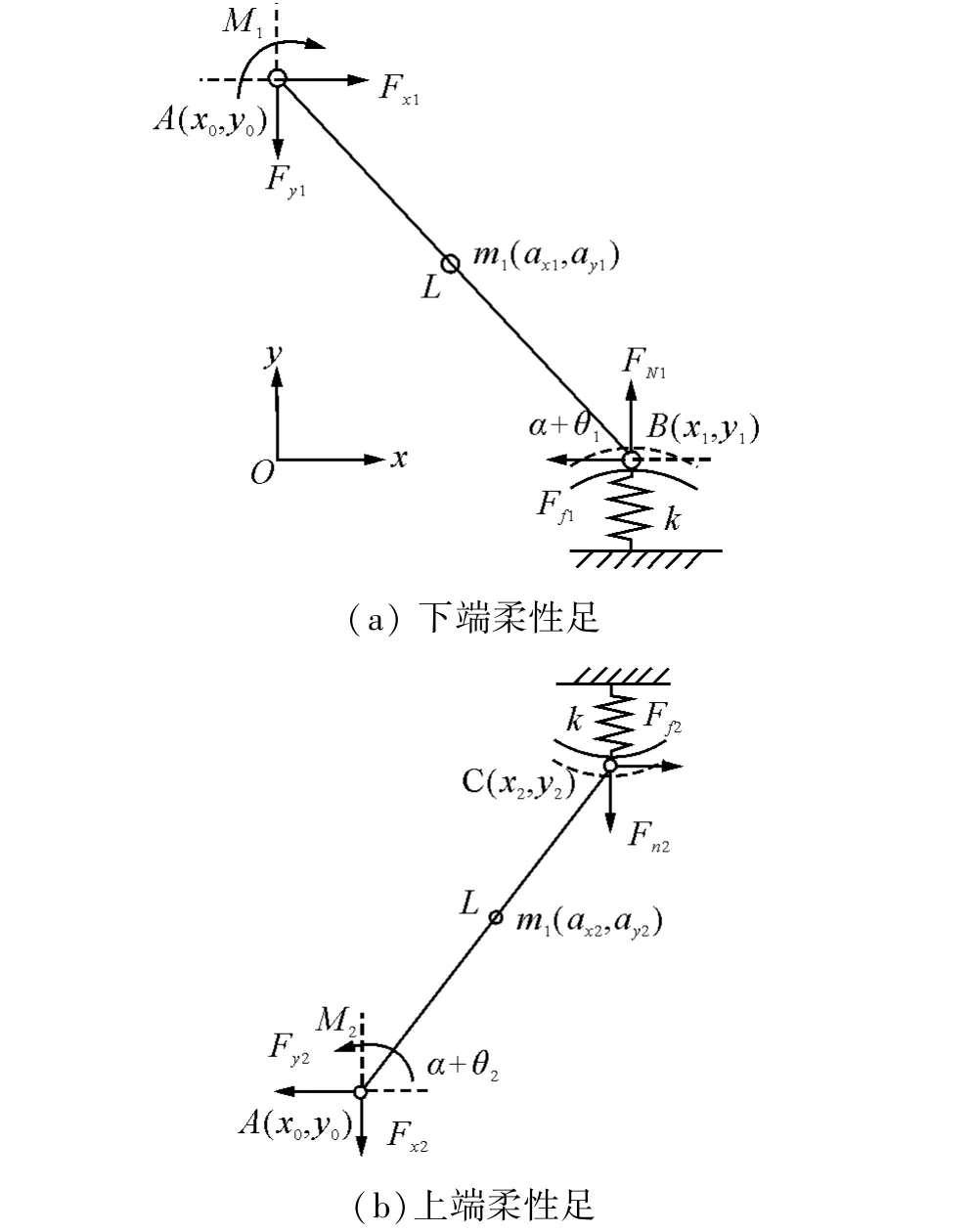
图4 简化动力学模型Fig.4 Simplified dynamic model

用F0sin（ωt）表示系统的激励，Fxi和Fyi为柔性足所受水平方向和竖直方向驱动力，FNi和Ffi表示足端与地面的法向与切向碰撞力，m0和m为基体和柔性足质量，Mi为扭簧i的扭转力矩，利用达朗伯原理，可得两端柔性足的动力学方程：

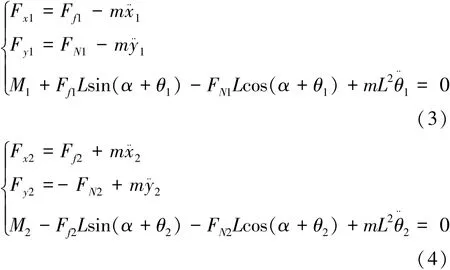
1.3 碰撞模型

柔性足与管壁的碰撞属于斜碰撞，碰撞为机构提供了驱动力，但同时也必然改变柔性足的运动状态，经典的瞬时碰撞模型不能处理存在摩擦的斜碰撞过程，也无法求得碰撞力。

假设碰撞发生时刻柔性足与管壁表面的接触是点面接触，碰撞过程中产生法向力和切向力，Hertz弹性碰撞理论可以用于描述此类碰撞的法向力。将地面约束简化成弹簧模型，采用非线性弹簧阻尼模型，法向力可以表示为

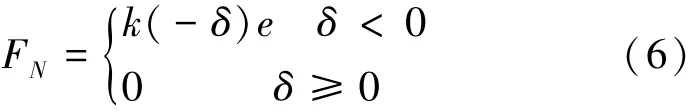
其中基体的动力学方程为

式中：k为法相碰撞刚度；e为非线性指数；δ为压缩量，以下端柔性足为例δ＝y1

e、k为描述法向力的碰撞参数，无法直接测量，但是可以通过参数辨识的方法得到。

由于柔性足结构及碰撞过程的特殊性，难以直接测量碰撞力和足端运动参数的变化，因此本文给定系统的初始条件，通过测量碰撞发生后柔性足末端运动速度的变化与仿真计算结果进行比较，以二者误差最小为目标，进行参数的分析与综合，从而实现对碰撞模型的参数辨识。

静态摩擦模型以Coulomb模型为代表，其计算量小、模型参数易于测量，在碰撞振动问题的研究中得到了广泛应用［8-11］。在斜碰撞中，采用 Coulomb模型描述切向碰撞力，以下端柔性足为例：

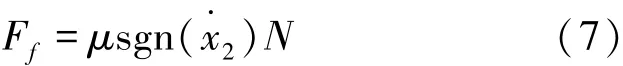
由式（7）计算得到的摩擦力在相对速度的符号发生改变时会突变，仿真步长过小使计算无法进行。因此，可以采用反正切函数来近似模拟摩擦力的突变，即

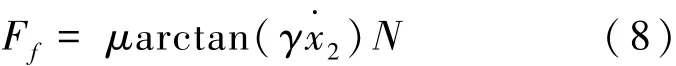
式中：μ为摩擦系数，γ为摩擦力曲线形状参数。

1.4 模型仿真分析

为了研究柔性足的动力学特性，并对其致动机理进行分析，依据以上的方程组，利用 MATLAB的Simulink工具箱建立系统的动力学模型。

取参数 L＝0.012 m，m0＝ 0.01 kg，e＝ 2，m＝0.000 8 kg，k＝1×108N／m，α ＝60°，γ＝10 000，F0＝10 N，f＝100 Hz，对上述模型进行数值仿真，得到发生碰撞的柔性足运动特性曲线如图5所示。

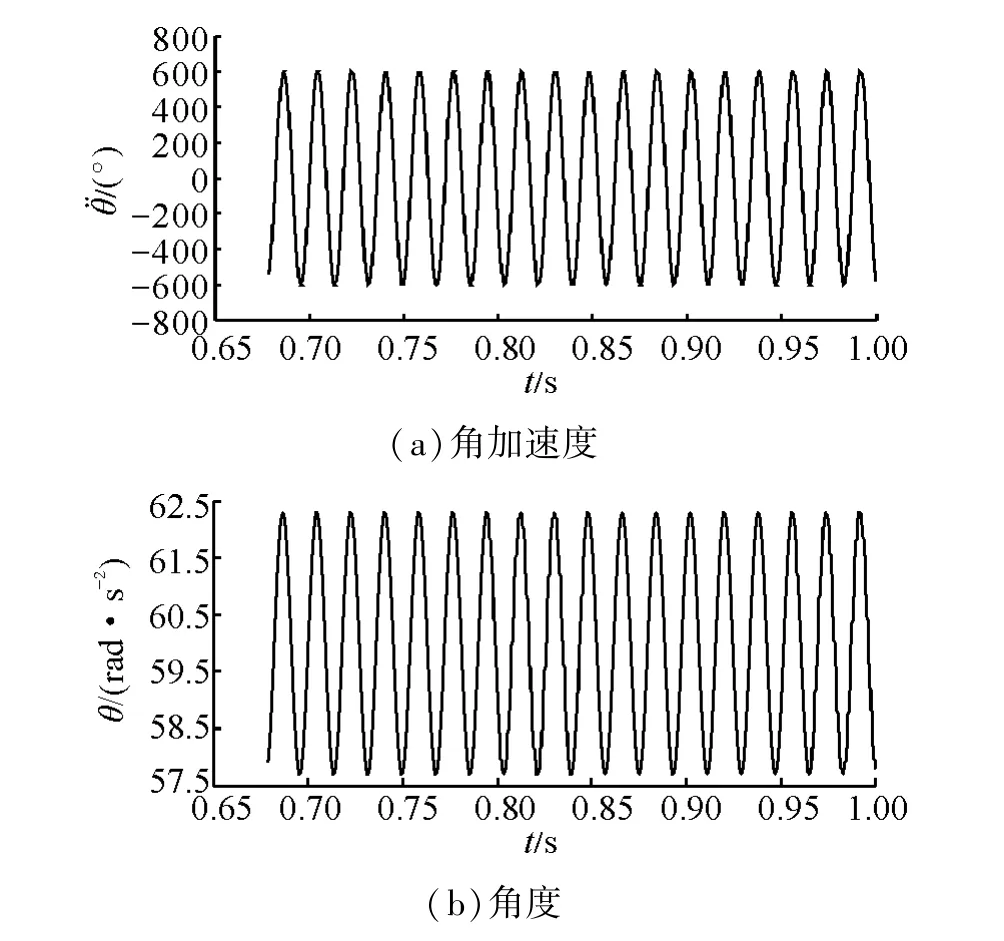
图5 柔性足角加速度、角度变化曲线Fig.5 The acceleration and angle curves of resonance foot

图5（a）中机器人柔性足与管壁碰撞的角加速度在一定范围内振荡变化，变化趋势和偏心轮转动时传递给柔性足的激励变化一致，最大角加速度约为θ¨

max≈600 rad／s2。图5（b）显示机器人柔性足角度变化曲线，初始状态时柔性足与管壁夹角为α＝60°，运动开始后柔性足的角位移θmax≈2.5°，由此可见，仿真模型的计算结果和理论中预期的机器人角加速度、相应的柔性足角度位置相符。

机器人样机简化模型仿真曲线如图6～8所示，样机在振动中柔性足和管壁碰撞产生切向力和法向力，驱动样机前进。

图6（a）为α＝60°时，样机在1.4、1.2、1 N不同激励振幅下水平方向位移仿真曲线，由图可见振幅越大，样机水平方向上的运动速度越快，所以激励振幅大小是影响机器人运动速度的因素之一。图6（b）为α＝60°时，样机在120、100、80 Hz不同激励频率下水平方向位移仿真曲线，可见激励频率改变，机器人的运动速度也会发生变化，且仿真中频率增大机器人运动速度也增大，可以预测120 Hz激励频率更接近机器人的固有频率，所以激励频率也是影响机器人运动速度的因素之一。

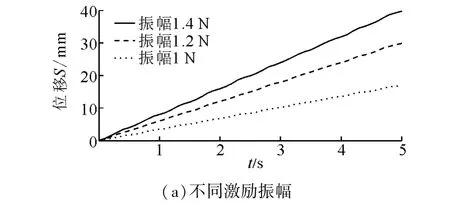
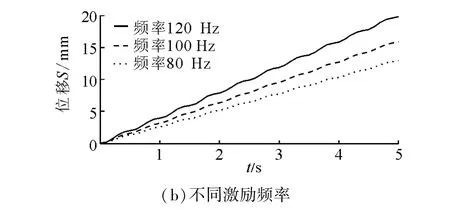
图6 α＝60°时不同激励下样机水平方向位移曲线Fig.6 The curve of different excitation prototype horizontal direction displacement when α＝60°

图7为样机在运动过程中垂直运动方向上的位移仿真曲线，由图可见竖直方向位移在平衡位置附近小幅震荡，这是由于样机在激励源带动下上下振动和柔性足与管壁碰撞时发生形变所致，与理论分析结果一致。

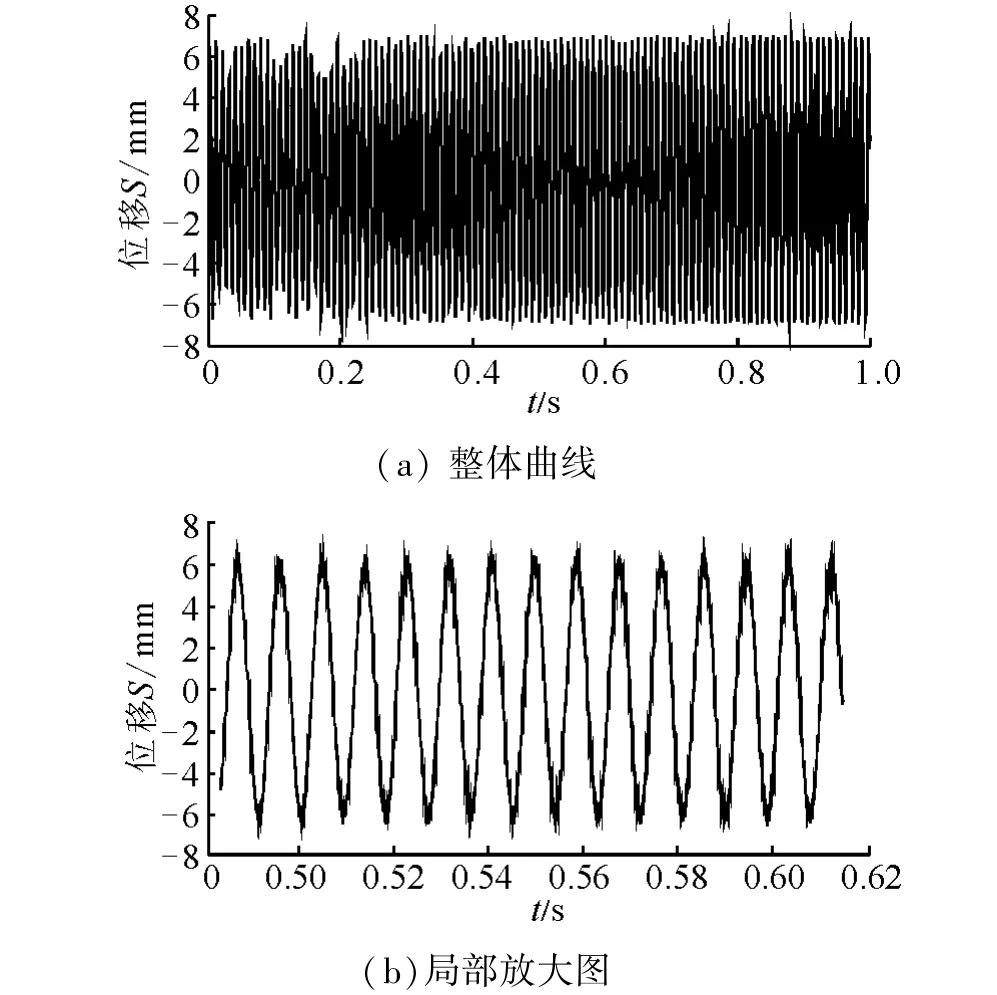
图7 样机竖直方向位移曲线Fig.7 The curve of prototype vertical direction displacement

图8为α＝85°时样机水平方向位移仿真曲线，管道机器人在初始阶段位移略有波动，随后很快趋于稳定，样机位移和运动时间基本成正比例关系。

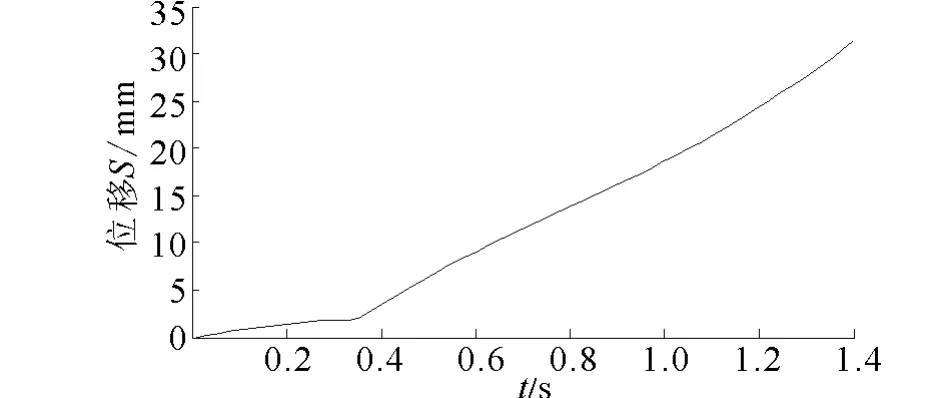
图8 α＝85°时样机水平方向位移曲线Fig.8 The curve of prototype horizontal direction displacement when α＝85°

2 样机与实验研究

机器人主体部分样机机构设计如图9所示，机器人采用节、端盖、柔性足装配方式，可用于批量化制作。在结构设计中节和端盖装配处含有内斜面，柔性足加工成梳齿状，装配在节与节、节与端盖的内斜面缝隙处。以此确保柔性足的角度一致性。

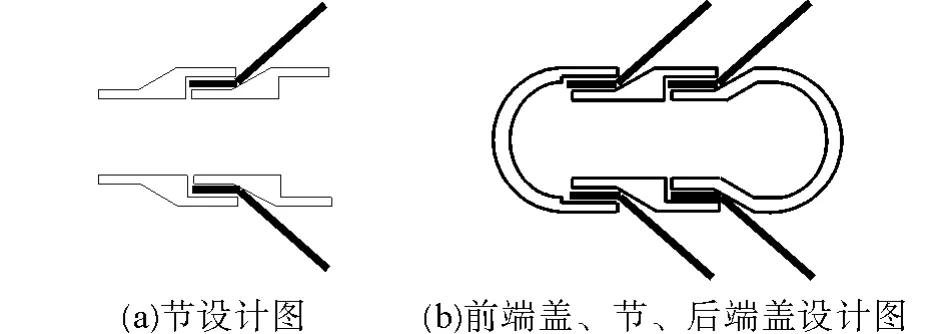
图9 样机机构设计图Fig.9 The design of prototype institutions

微型管道机器人样机其激励源采用低功耗、6mm空心杯微型直流电机。工作时将电机固定于特制的弹性支架中，利用微型电机带动偏心轮转动产生振动，微型电机式管道机器人样机如图10所示。

图10 微型电机式管道机器人样机Fig.10 The prototype of micro-motor pipe robot

对机器人样机进行运动速度测定实验，主要研究理论分析中柔性足角度和激励振幅对样机运动速度的影响。

样机速度测试实验原理如图11所示，截取一段长度为100 mm的测试区间，在运动的起点与测试区之间有一段加速区，机器人运动到测试区时已经完成加速进入匀速运动过程。当机器人触发左侧光电传感器开始计时，触发右侧传感器则计时结束，测试区的长度除以计时时间为机器人的运动速度。

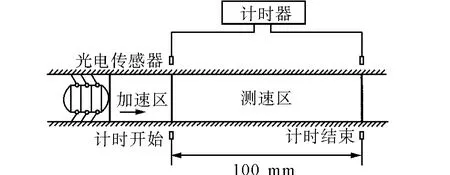
图11 样机速度测试实验原理图Fig.11 Experiment principle map of prototype speed testing

首先将激励电压幅值固定为8 V，改变柔性足角度（20°～90°），每个角度进行10组测试；然后将激励电压每次减小1 V，重复以上实验过程，测得实验数据。根据上述实验数据，可得到柔性足与管壁不同角度下运动速度随激励电压的变化曲线（如图12（a））、和不同激励电压下运动速度随柔性足角度的变化曲线（如图12（b））。

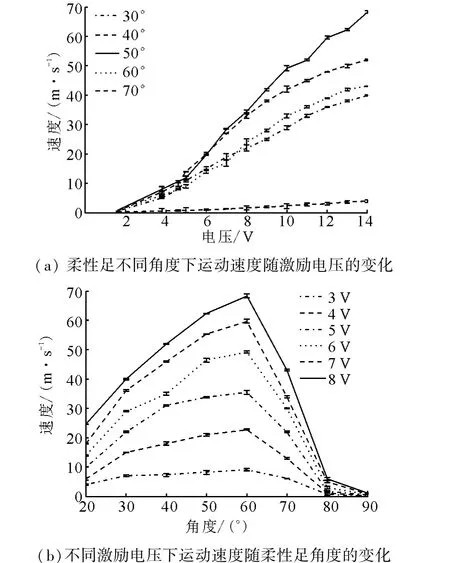
图12 速度变化曲线Fig.12 Speed curves

试验结果表明直径为 15 mm，最小长度为22 mm的管道机器人，激励电压为8 V，柔性足夹角为60°时运动速度最高，约为68.29 mm／s。

3 结束语

微小型管道机器人可携带微型照明、成像装置和诸如湿度、温度等多种微型传感器，用以实现工业微型管道的检测和修理。本文建立了管道机器人运动力学模型，对机器人运动机理进行了理论分析和实验研究。实验表明，激励频率、激励振幅、柔性足与管壁间夹角均可影响机器人运动效果。机器人尺寸为15 mm×15 mm×22 mm，当激励电压为8 V，柔性足夹角为60°时，运动速度可达68.29 mm／s。采用谐振驱动原理有效提高了机器人的运动效率，减少了复杂的机械结构，可以使机器人在细小管道内灵活运动。本文的研究为微型机器人的后续研究奠定了基础，对连续体型机器人在管道环境内的运动控制也具有一定参考意义.

在今后的研究中，还将集中于生物医疗等领域，如肠道内表面行走机理研究、基于谐振驱动原理的肠道内窥机器人研究和机器人结构改进等问题上，包括机器人的密封、发热以及可靠性等。

［1］李鹏，马书根，李斌，等.具有自适应能力管道机器人的设计与运动分析［J］.机械工程学报，2009，45（1）：154-161.

LI Peng，MA Shugen，LI Bin，et al.Design and motion analysis of an in-pipe robot with adaptability to pipe diameters［J］.Journal of Mechanical Engineering，2009，45（1）：154-161.

［2］唐德威，李庆凯，姜生元，等.具有差动运动功能的管道机器人设计与分析［J］.机械工程学报，2011，47（13）：1-8.

TANG Dewei，LI Qingkai，JIANG Shengyuan，et al.Design and analysis of a pipeline robot with the function of differential movement［J］.Journal of Mechanical Engineering，2011，47（13）：1-8.

［3］林蔚，颜国正，王志武，等.基于微型电机的肠道机器人机构设计［J］.机器人，2011，33（3）：319-323.

LIN Wei，YAN Guozheng，WANG Zhiwu，et al.Mechanism design of an intestinal robot based on micro-motor［J］.Robot，2011，33（3）：319-323.

［4］JUNGWAN P，TEAHYUN K.Development of an actively adaptable in-pipe robot［C］／／Proceedings of the 2009 IEEE International Conference on Mechatronics.Malaga，Spain，2009：1-6.

［5］YUICHI N，YUKIHIRO S，SHIGEKI.Development of an inpipe micro mobile robot using peristalsis motion［J］.Journal of Mechanical Science and Technology，2010（24）：51-54.

［6］ZHAO Y X，HE G P，GAO D W，et al.Micro in-pipe robot mechanical structure design of shape memoryalloy driving［C］／／Proceedings of the 2009 IEEE International Conferfence on Robotics and Biomimetics.Guilin，China，2009：360-365.

［7］陈西平，杨志刚，程光明，等.谐振型压电式管内移动机构［J］.吉林工业大学学报：工学版，2002，32（1）：28-32.

CHEN Xiping，YANG Zhigang，CHENG Guangming，et al.On the in-pipe locomotive mechanism using resonance piezoelectric vibrators［J］.Journal of Jilin University：Engineering and Technology Edition，2002，32（1）：28-32.

［8］蒋振宇，李伟达，祝宇虹.一种谐振式微小型机器人移动机构［J］.压电与声光，2010，32（4）：625-628.

JIANG Zhenyu，Li Weida，ZHU Yuhong.A micro locomotion mechanism based on the resonance［J］.Piezoelectrics＆Acoustooptics，2010，32（4）：625-628.

［9］孙立宁，李伟达，李满天，等.基于碰撞力的谐振致动机理与试验［J］.机械工程学报，2010（9）：12-18.

SUN Lining，LI Weida，LI Mantian，et al.Experiments and resonant locomotion principle based on impact force［J］.Journal of Mechanical Engineering，2010（9）：12-18.

［10］LIU P K，WEN Z J，LI J.A piezoelectric in-pipe micro robot actuated by impact drive mechanism［J］.Optics and Precision Engineering，2008，16（12）：2320-2326.

［11］EIGOLI A K，VOSSOUGHI G R.Dynamic modeling of stick-slip motion in a legged，piezoelectric driven microrobot［J］.International Journal of Advanced Robotic Systems，2010，7（3）：201-208.

［责任编辑：王亚秋］

Design and experiment of a micro in-pipe robot based on the resonance

LIU Lei，LI Juan，LI Weida，QIN Jia

（School of Mechanical and Electric Engineering，Soochow University，Suzhou 215021，China）

A micro robot is described in this paper that will conduct its work in a thin pipe with a small diameter in the range of 18 mm to 30 mm which is hard to detect.The robot is based on the resonant driving principle，which simplifies the transmission mechanism.Using an excitation source－the eccentric wheel is driven by a micro engine.A mathematical model of the robot in the pipe wall constraints was established to solve the angular acceleration caused by the collision between the robot＇s feet which are flexible enough with the pipeline wall，and the position of the contact points.The movement mechanism of the robot was also analyzed.The robot prototype was designed and a pipeline test environment was built to carry out the speed and traction testing.The minimum size of the prototype is 15 mm×15 mm×22 mm.The results show that：under 8 V voltage，the maximum speed of the prototype is up to 68.29 mm／s，the power consumption is about 0.15 W，and the maximum ramp angle is 30°.

nonlinear vibration；pipeline robot；resonant drive；structure design

10.3969／j.issn.1006-7043.201305066

TP242

A

1006-7043（2014）08-1002-06

http：／／www.cnki.net／kcms／doi／10.3969／j.issn.1006-7043.201305066.html

2013-05-23. 网络出版时间：2014-06-17 15：39.

国家自然科学基金青年基金资助项目（61105106）；江苏省自然科学基金基础研究计划资助项目（BK2011379）.

刘磊（1988-），男，硕士研究生；李娟（1978-），女，副教授，博士.

李娟，E-mail：lijuan＠suda.edu.cn.