基于NSGA算法的公交车辆调度优化模型

宋晓鹏， 韩 印， 姚 佼

（上海理工大学管理学院，上海 200093）

基于NSGA算法的公交车辆调度优化模型

宋晓鹏， 韩 印， 姚 佼

（上海理工大学管理学院，上海 200093）

公交车辆调度方案的优化对于提高公交服务水平，促进公交事业的快速发展至关重要.在乘客与公交公司利益博弈的基础上，基于极小极大思想，考虑公交车车辆容量的限制及城市道路信号控制的干扰因素，建立公交发车间隔优化模型，并利用非支配排序遗传算法（NSGA）进行模型的求解.以河南省焦作市的公交线路为例进行验证，优化结果显示乘客的平均等车时间相对减少48.3%，公交车的全日平均满载率下降了3.8%，公交服务水平有所改善.

城市公交；发车间隔；等车时间；非支配排序遗传算法

优先发展城市公共交通是提高交通资源利用效率、缓解交通拥堵的重要手段.作为城市交通的主要通行方式，公共交通服务水平与居民出行需求和城市交通运行状态息息相关.优化发车间隔是公交调度的主要技术手段.准确和高效率的发车调度对提高公交线路的服务能力，减少居民的出行延误，提高乘客满意度有着重要意义.Huisman等［1］提出了用于描述多场站调度问题的动态模型，并应用“聚类再生成”启发式算法，基于数学规划模型得出优化的结果，但对公交车容量未作考虑.孙芙灵［2］根据乘客需求来确定发车间隔，用数学规划的思想建立调度模型，并用时间步长法、等效法进行求解，得出仿真结果，但对公交公司利益考虑不足.陈芳［3］根据客流变化规律，对发车间隔采用多时段处理思想，建立了以乘客与公交企业运营费用最小为目标的公交车辆调度模型，对于信号控制的干扰没有进行考虑.刘志刚等［4］根据区域公交调度模型，把公交车容量作为理想状态，不受信号控制的干扰，建立了公交调度系统双层规划模型.本文综合考虑乘客与公交公司利益，并基于极小极大思想，考虑公交车车辆容量的限制及城市道路信号控制的干扰因素，建立公交发车间隔优化模型，并利用非支配排序遗传算法（NSGA）进行模型的求解.

1 优化模型的建立

1.1模型假设

公交车辆的运营受很多因素的影响，本文为建立公交调度优化模型作出以下假设：

a.线路上的公交车辆为同一型号，公交车会按照调度表准时到站和出站；

b.全程票价统一；

c.公交车辆行驶过程中不存在阻塞现象及突发情况，且公交车之间依次行进，不存在超车及越站现象；

d.各站点乘客上下车的时间、公交车在各站点的停留时间均被考虑在公交车的平均速度之内；

e.仅考虑沿线信号延误干扰，沿线交叉口具有相同的信号延误；

f.各交叉口有足够大的通行能力，仅考虑单行方向公交车运行.

1.2 模型的构建

公交车运行调度模型的建立是一个复杂过程，根据极小极大思想，为使服从相同规律的受控群体的性能指标在总体上最小，其充分条件就是使群体中性能指标值最大的个体值最小.作为乘客希望获得便捷、舒适、车辆间隔小、等待时间短的公交服务，这样势必造成空驶率过高，公交公司的利益得不到保证而影响其服务质量.而公交公司希望发车间隔增大，发车次数少且载客量大，以获取更大利益，这与乘客的需求相违背.因此，综合考虑公交公司与乘客的利益，使乘客最大广义费用最小及公交公司最大广义费用最小.

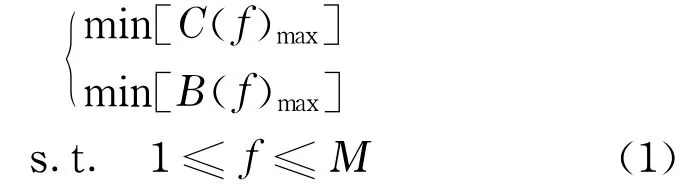
式中，M为公交车的最大发车间隔，为一正常数；f为发车间隔，f为整数，min；C（f）为在时间T内，乘客的广义费用，元；B（f）为在时间T内，公交公司广义费用，元.

在时间T内出行者的广义费用为

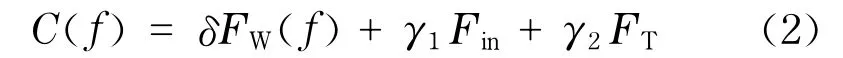
式中，δ为与乘客有关的时间费用转化系数；FW（f）为乘客等车时间，min；γ1为相对于等车时间费用的在车时间费用权重系数；γ2为相对于等车时间费用的换乘惩罚费用权重系数；Fin为与在车时间相关的费用；FT为与换乘相关的惩罚费用.

关于乘客等车时间有

式中，FW（f）为所有出行者等待时间，min；n为所有等待的乘客数量，人次；S为乘客等待时间的均值，min.

对于某一站点，记W（t）为t时刻在节点等待的乘客数量.等待的乘客包含在下一辆车到达之前陆续来到站点作等待的乘客及在上一运次滞留的乘客.t时刻为某一公交车进站时刻.并且设定公交车的容量为C，则在该站点乘客上车的数量为P（t）.

式中，O（t）为在某站点处，公交车上已有的乘客数量.

对于滞留的乘客，需要等待下一运次才能乘上公交车，假定不存在3次等车，而保证一定的服务标准，对于滞留的乘客需要再次等待一个ti时间才能上车.若对于上一时刻存在乘客滞留，则滞留人数为D（t-ti）.

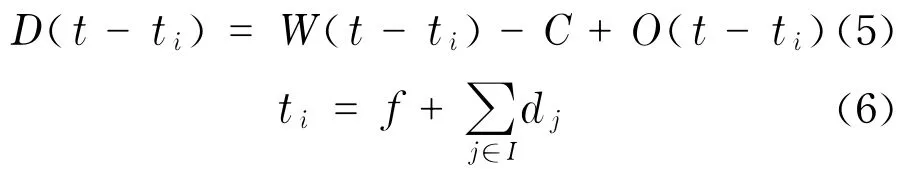
式中，ti为相邻运行公交的平均车头时距，min；d为T时间段内，公交车由于遇到交叉口信号控制的干扰引起的平均延误，min；dj为公交车遇到某一交叉口j引起的平均延误；I为公交车所沿该线路中交叉口数量，I为整数.

由于公交车按照行车时刻表运营，因此，乘客到达公交站点会产生等车时间.根据Bowman等［5］提出的等车时间模型，乘客期望等待时间的均值为

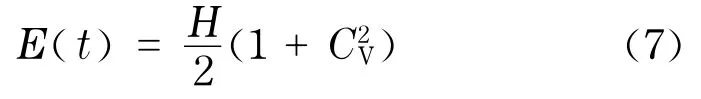
式中，E（t）为乘客期望等车时间，min；H为平均车头时距，min；CV为车头时距协变参数.

如果排除外界干扰，公交车平均车头时距应与发车间隔相等.由于公交车运行受交叉口信号控制的干扰，车头时距发生波动，则平均车头时距为ti.

而对于t时刻，等候车辆的总人数为n，引起乘客等待公交车的状态有m种，分别为没有滞留的乘客平均等待时间和滞留乘客平均等待时间这两种方案，即m=2.根据熵权决策法原理［6］得出乘客等待时间的均值为

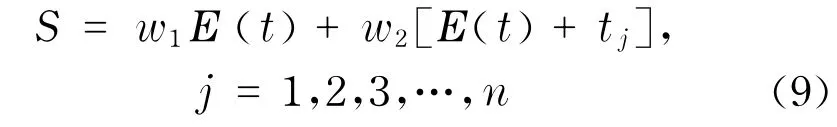
式中，w1为没有滞留的乘客等待时间权重；w2为滞留乘客等待时间权重.

出行者等待时间

由于乘客在车时间只与路段的不同而不同，因此定义在车时间费用是只与路段相关的常数.对于惩罚费用同样与发车频率无关，取决于路段，同样可以作为常数处理［7］.对于在车时间费用与惩罚费用相应权重可以通过实际调查统计得到［8］.在时间T内，相应公交车运营的广义费用为

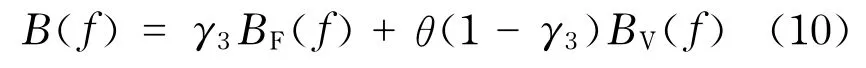
式中，γ3为公交公司所支出的固定费用的相应权重；BF（f）为在时间T内公交公司所支出的固定费用，元；θ为每公里运营费用（与百公里燃油有关），元／km；BV（f）为在时间T内与发车间隔相关的公交车辆行驶里程，km.

其中固定费用主要包含公交车的保养维修费用、公交公司的管理费用及员工工资［9］，在T时段内可得到的相应固定费用为

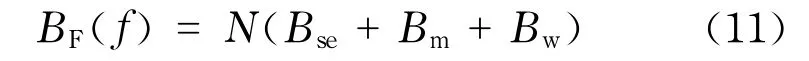
式中，Bse为在T时段内，平均每辆车的保养维修费用，元；Bm为在T时段内平均每辆车的管理费用，元；Bw为在T时段内相对于每辆车的人均工资费用，元.

在T时段内运营了N辆车，则

式中，N为一整数，运算中中括号为取整运算，表示N为不超过T／f的最大整数.

所有车辆行驶里程

式中，v为公交车的平均行程速度，在某条干线上为一常数，km／h.

公交车辆的运行势必受到红绿灯的干扰而影响正常运营，为保障公交车服务标准，相邻运行中的公交车车头时距因交叉口信号干扰需保持在一个发车间隔内.公交车遇到交叉口引起的延误是随机的［10］，因而根据Miller提出的随机延误理论得到

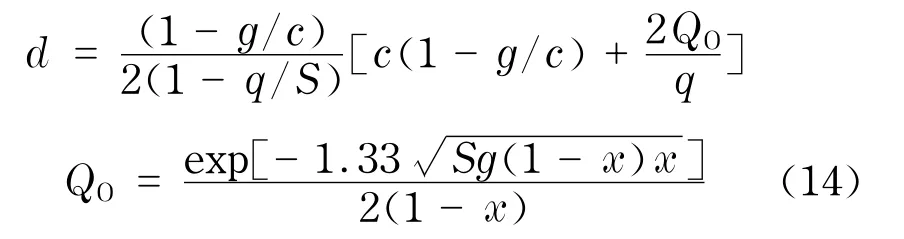
式中，d为T时段内，公交车由于遇到交叉口信号控制的干扰引起的平均延误，min；c为周期时长，min；g为有效绿灯时长，min；x为饱和度；q为到达率；QO为平均饱和排队车辆数，辆.

公交车遇到交叉口引起的总的延误满足如下约束

基于公交公司与出行者综合广义费用最小，公交车发车间隔与信号控制之间存在相互影响，交通信号控制影响着车头时距的波动程度，约束发车间隔的确定.发车间隔的合理性又反映了信号控制的优化程度，信号控制得以优化可减少公交车运行时由于交叉口的干扰引起的延误，提高通行能力.根据以上分析，建立如下公交车运行调度模型

对于公共交通，当交通需求增加时，提高发车频率，可使乘客的等车时间减少［11］.为保证优化结果较优，相邻运行公交车不发生超车或前后相接的现象.

2 模型的求解

乘客广义费用和公交公司的广义费用这些目标并不是彼此独立，二者耦合在一起，互为矛盾，互为竞争.某子目标的改善可能引起其它子目标性能的改变，而同时使所有子目标达到最优往往是不可能的.要找到这些目标的最佳设计方案，就要解决多目标与多约束的优化问题，即多目标优化［12］.对于模型的求解引进NSGA.

可以定义为在一组约束条件下，极小化这两个目标函数［13］，令［C（f）］max=u1（X），［B（f）］max= u2（X），形式如下：

式中，X=（f1，f2，…，fp）是一个p维向量，ui（X）是目标函数，i=1，2.gj（X）和hk（X）为系统约束.

NSGA是基于对个体的几层分级实现的.在选择执行前，群体根据支配与非支配关系来排序，所有非支配个体被排成一类，这些被分级的个体共享它们的虚拟适应度值.然后忽略这组已分级的个体，对种群中的其它个体按照支配与非支配关系再进行分级，该过程继续直到群体中的所有个体被分级.在NSGA中对每个局部的Pareto曲面（线）上的所有个体分别采用适应度共享策略，有利于保持群体多样性，可以克服超级个体的多度繁殖，防止早熟收敛.根据关志华［14］对于非支配排序遗传算法算子分析，参数选取分别为：交叉概率取0.8；共享半径取0.05；变异概率取0.00.算法流程如图1［13］所示.

图1 NSGA算法流程图Fig.1 NSGA flow chart

3 实例分析

由式（9）知乘客的平均等待时间与发车间隔具有一定的关联性.此外，董强等［15］对公交车调度问题研究表明发车间隔与公交车的满载率相关.由于车次与发车时刻一一对应，而车辆的队列顺序不发生改变，因而对所需车辆进行统一标号后，则每一车次与其对应的车辆编号是确定的.直接对第k次车进行考察，公交车全日平均满载率为

式中，λS为公交车全日平均满载率；μ为某一站台；λ（k，μ）为第k次车离开第μ站时的全日平均满载率；TN为一天单程所发的车次总数；μA为单程站台总数；Tday为公交车全日运行时间.模型相关参数取值见表1.

选取河南省焦作市具有代表意义的5条公交线路，如图2所示，分别为21路、9路、13路、17路、14路.乘客平均等待时间能够直观地反映乘客的出行利益，公交车辆全日平均满载率能够衡量车辆的利用程度，反映了公交公司的利益.因此，以乘客平均等待时间和全日平均满载率作为评价指标，进行相关的调查分析.经实地调查，上述模型相关参数选取如表1所示.

表1 模型相关参数取值Tab.1 Selection of model related parameter

在实际调查中，线路21路、9路由于客流量较大，满载率较高，对乘客来说舒适性下降，不利于乘客利益；线路17路、14路，乘客等待时间太长，吸引客流较弱，不利于乘客利益，满载率过低，车辆利用程度较低，影响公交公司利益.对于满载率，各个城市都没有形成统一的规范值.按照焦作市城市公交行业管理规范规定，为保持车辆利用程度，全日线路平均满载率控制在60%～100%.线路13路满载率维持在合理水平，乘客等待时间稍长，可适当调节，维持乘客利益.通过Matlab对上述算法进行实现，利用模型对21路、9路、13路、17路、14路公交线路发车间隔进行优化，优化结果以乘客平均等待时间和公交车平均满载率为衡量指标，如图3与图4所示.

图2 焦作市5条公交线路走向图Fig.2 Five bus routes to figure in Jiaozuo

图3 各线路优化前后乘客平均等待时间比较Fig.3 Comparison between average passenger waiting times before and after optimization

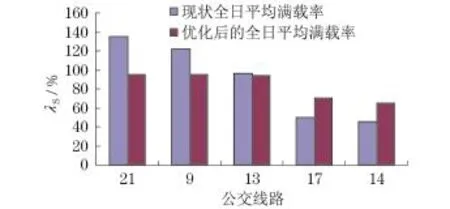
图4 各线路优化前后全日平均满载率比较Fig.4 Comparison between diurnal average load factors before and after optimization

根据本研究的优化结果，各线路乘客平均等待时间及对应的全日平均满载率不仅满足焦作市城市公交行业管理规范中的规定，且各线路总的平均满载率减少了3.8%，舒适度增加，吸引了客流，保证了公交公司的相应利益.同时，乘客平均等车时间相对于现状平均等待时间减少48.3%，满足乘客的利益.

4 总 结

兼顾公交公司与出行者的利益愿景，根据极小极大思想对公交车发车间隔进行了优化.运用非支配排序遗传算法解决此类多目标问题，并获得最优解组合集合，在集合中找到最优解，规避了同时使所有子目标均达到最优的不实际现象.充分考虑了公交车容量限制产生的乘客滞留状况和交叉口信号控制对公交车运行的影响.通过对发车间隔的优化，不仅能满足客流需求，同时规避了公交资源的浪费，具有现实适用性.

［1］ Huisman D，Freling R，Wagelmans AP M.A robust solution approach to the dynamic vehicle scheduling problem［J］. Transportation Science，2004，38（4）：447-458.

［2］ 孙芙灵.公交调度中发车间隔的确定方法的探讨［J］.西安公路交通大学学报，1997，17（2B）：44-48.

［3］ 陈芳.城市公交调度模型研究［J］.中南公路工程. 2005，30（2）：162-164.

［4］ 刘志刚，申金升.区域公交时刻表及车辆调度双层规划模型［J］.系统工程理论与实践，2007，27（11）：135 -141.

［5］ Bowman L A，Tumquist M A.Service frequency：schedule reliability and passenger wait times at transit stops［J］. Transportation Research，1981，15（6）：465-471.

［6］ 闫文周，顾连胜.熵权决策法在工程评标中的应用［J］.西安建筑科技大学学报，2004，36（1）：98-100.

［7］ 高自友，任华玲.城市动态交通流分配模型与算法［M］.北京：人民交通出版社，2005.

［8］ 何胜学.道路拥挤收费定价分析［J］.上海理工大学学报，2005，27（1）：87-90.

［9］ 陈国栋，李会芬.公交车的经济寿命和影响因素的研究［J］.广西大学学报，2008，30（zl）：211-212.

［10］ 何胜学，范炳权，严凌.公交网络最优路径的一种改进求解算法［J］.上海理工大学学报，2006，28（1）：163-167.

［11］ Rea J C.Designing urban transit systems：an approach to the route technology selection problem［J］.Highway Research Record，1972（417）：48-59.

［12］ 付立，窦明罡，朱建凯，等.非支配排序遗传算法的改进［J］.计算机与数字工程，2011，39（2）：11-15.

［13］ 高媛，卢建刚.非支配排序遗传算法（NSGA）的研究与应用［D］.杭州：浙江大学，2006.

［14］ 关志华.非支配排序遗传算法（NSGA）算子分析［J］.管理工程学报，2004，18（1）：57-60.

［15］ 董强，刘超慧，马熠.公交车调度问题的研究［J］.工程数学学报，2002，19（2）：60-66.

（编辑：丁红艺）

Bus Scheduling Optimization Model Based on NSGA Algorithm

SONGXiao-peng， HAN Yin， YAOJiao
（Business School，University of Shanghai for Science and Technology，Shanghai 200093，China）

Optimized buses scheduling scheme is essential to improve transit service levels and promote rapid development of public transport.Taking account of the interest game between passengers and bus company and considering the vehicle capacity constraint of buses and confounding factors of urban road signal control，a bus departure interval optimization model was built in the light of the minimax idea，and then the non-dominated sorting genetic algorithm（NSGA）was used to solve the model.The case of bus lines in Jiaozuo，Henan Province，was taken as an example to illustrate the improvement of transit service levels due to the optimization scheduling.The results show that the average waiting time of passengers is reduced by 48.3%and the average load factor of buses per full day is decreased by 3.8%.

urban public transport；departure interval；waiting time；non-dominated sorting genetic algorithm

U 491

A

2013-08-08

国家自然科学基金资助项目（51008196）；上海市一流学科建设资助项目（S1201YLXK）

宋晓鹏（1987-），男，硕士研究生.研究方向：智能交通、交通规划与管理.E-mail：songxiaopeng208＠163.com

韩 印（1964-），男，教授.研究方向：智能交通、交通规划与管理.E-mail：hanyin2000＠sina.com

1007-6735（2014）04-0357-05

10.13255／j.cnki.jusst.2014.04.010