模块化多电平逆变器电容电压及环流控制

陈耀军 陈柏超 袁佳歆 田翠华

（1.武汉大学电气工程学院 武汉 430072 2.空军预警学院黄陂士官学校 武汉 430019）

1 引言

模块化多电平变换器一经提出[1,2]，由于其独特的优点[3]，在高压直流输电[4]、STATCOM[5,6]、SVG[7]以及电机驱动[8]等领域获得了广泛的关注。根据工作特性，该变换器存在着整流及逆变两种工作模式，作为逆变器，这种结构可以用在直流输电及中高压电机驱动等领域，此时称该变换器为模块化多电平逆变器。

相比于其他逆变器，模块化多电平逆变器可以实现电容电压的控制，从而保证输出电压的稳定。模块化多电平逆变器的一个重要特点是相间存在着环流，文献[9,10]对环流进行了定义，环流是不能够直接测量、但确实存在的变量。环流中存在着直流成分和谐波成分，如何实现环流的控制是研究的热点。文献[8-10]通过对环流的平均值进行控制，从而达到稳定电容电压的目的，但并没有提出环流谐波的抑制策略。文献[11-14]把桥臂等效为一个可变电容，并将桥臂作为一个控制的整体，采用变量在线估计及开环的方法实现了电容电压及环流谐波的抑制，但这种方法依赖于精确的系统参数，控制算法比较复杂。文献[15]在分析了环流二次谐波呈负序分布的基础上，把三相环流变换到两倍基波频率的dq坐标系中，实现环流二次谐波的抑制，通过仿真证实了该策略的可行性，但其并未考虑环流谐波其他成分，且没有给出实验研究结果。

假设同一桥臂电容电压是均压的，即具有相同的电压，本文首先建立了系统的单相状态方程，其变量为环流、输出电流，反映正负桥臂电容电压之和的变量以及反映正负桥臂电容电压之差的变量。基于此方程，定性分析了环流及电容电压的谐波成分，研究表明环流谐波除二次谐波外，还存在四次及以上的偶次谐波。通过坐标变换，把三相状态方程变换到两倍基波频率的dq0坐标系中，dq坐标系的方程表达了环流的谐波特性，零序坐标系的方程体现了电容电压的直流分量及环流直流分量的变化特性，其和dq坐标系中的方程是解耦的。基于此，本文提出了电容电压及环流的一种解耦控制方案，在零序坐标系中控制电容电压及环流的直流成分，而在dq坐标系中实现对环流的抑制，两个控制器彼此之间互不影响，相对文献[15]，其中对环流谐波的抑制进行了改进，使其避免了环流四次及以上偶次谐波的影响。最后通过仿真和实验证实了文中结论的正确性。

2 系统的基本结构及原理

三相模块化多电平逆变器的拓扑结构如图1所示，每相有正、负两个桥臂（分别对应为上、下桥臂），每个桥臂由 N个完全相同的半桥模块和一个电感串联组成。半桥的上、下开关管互补工作，以控制模块电容接入电路或旁路，从而改变桥臂的电平数量。正常工作时，通常保证每相有N个模块电容被接入电路，每个模块电容的平均电压为Vd/N，Vd为输入直流电压。为获得多电平的正弦波输出，可以采用最佳电平逼近法[16]、载波移相调制方法[17,18]或载波重叠PWM调制法[11-14]。

图1 模块化多电平变换器拓扑结构Fig.1 The topologic structure of the modular multilevel converter

以u相为例进行分析。假设模块电容均压，即同一桥臂所有模块电容具有相同的电压，不考虑系统的载波谐波成分，正、负桥臂的基波电压 vPu和vNu可以写成[13]

式中，mu和φu为u相的幅度调制比及调制波相位；和分别为正负桥臂电容电压之和，用开关函数来表示，vPu和vNu可以简写成

式中，Su为u相的开关函数基波分量，Su=musin(ωt+φu)。在图1中，iu为负载电流，iZu为环流，环流在电路中存在，但不能被直接测量，这些电流满足如下方程[8-10]：

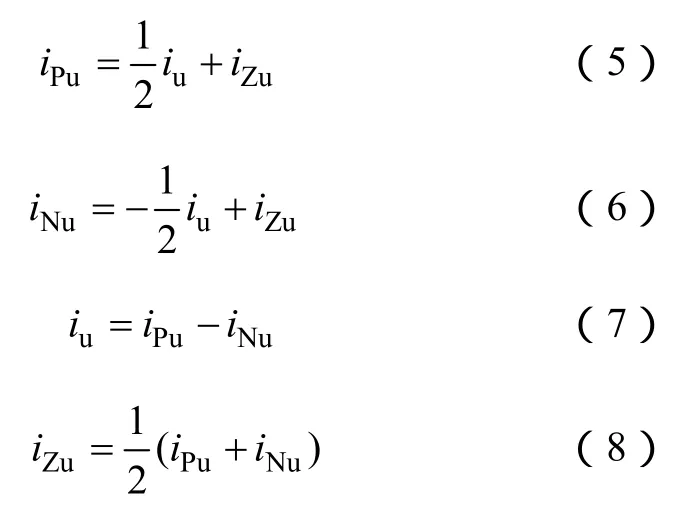
式中，iPu和 iNu分别为流过正、负桥臂的电流；rd为桥臂的等效直流电阻。根据图1，并考虑式（5）～式（8）的关系，可以得到输出电压和环流的方程为[13]

从式（9）和式（10）可以看出：输出电压取决于正、负桥臂的电压差，而环流取决于正、负桥臂电压和，这是环流控制的基础。

3 系统状态方程

任意电容功率可表示成

式中，vCi表示电容电压的瞬时值。以u相为例，假设电容是均压的，并且同一桥臂所有电容电压是相同的，则正负桥臂所有电容功率之和可分别表示为

式中，vPui和vNui分别为正、负桥臂第i个模块的电容瞬时电压。

根据功率平衡关系，可以得到

整理式（12）～式（15），则可得到

式中，C/N=CΣ。令 Cdc=2CΣ，Cac=8CΣ，vdc=

根据定义，式（9）和式（10）可以写成

把式（16）～式（19）写成矩阵形式

式中，p为微分算子， Z =diag（ LdcLacCdcCac），

式（20）反映了系统环流、输出电流、正负桥臂电容电压和以及正负桥臂电容电压之差之间的关系。根据式（20）可以画出单相MMC的一种等效电路，如图2所示。图中T1、T2是一个理想逆变器模型，其输入输出特性和逆变器相同。根据图2的关系可知：系统通过反映正、负桥臂模块电容电压和的电容Cdc和逆变网络T1将直流能量变为交流能量向外提供，而反映正、负桥臂模块电容电压差的电容 Cac影响着输出电压或环流。与此同时，环流同样影响着正、负桥臂电容电压差。

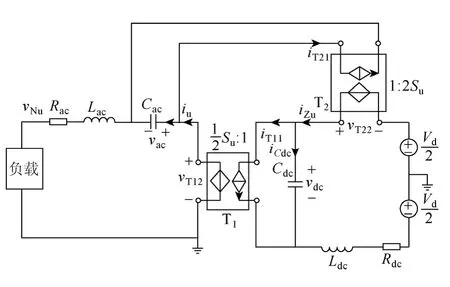
图2 系统单相等效电路Fig.2 The single phase equivalent circuit of the system

4 电容电压及环流控制

4.1 环流谐波定性分析

根据图2的关系，可得电容 Cdc流出的电流可以表示为

式中，φu为u相调制波相位；φIu为输出电流相对于调制波相位。由式（21）可知，iT11含有直流分量和二次谐波分量，其直流分量用于为负载提供有功功率，而二次谐波分量则表现为无功特性。

显然，稳态时，环流iZu必然含有与iT11相同的直流分量，iT11中含有二次谐波分量，该二次谐波电流会在电容Cdc中产生二次谐波电压vdc，从而在直流侧产生二次谐波电流，可见，在环流iZu中必然含有直流及二次谐波电流。

通过网络T2的作用，环流的直流分量和二次谐波分量会在 T2的一次侧产生基波及三次谐波电流流进电容Cac，从而在电容Cac中产生基波及三次谐波电压，输出电流也会在电容Cac中产生基波电压。通过网络T2的作用，电容Cac的基波及三次谐波电压会在直流侧产生二次及四次谐波电压，从而引起新的二次及四次谐波环流，该新产生的四次谐波环流通过网络T2的反作用会在电容Cac中产生五次谐波电压，该五次谐波电压又会在直流侧产生六次谐波环流…，如此反复，电容 Cac中会产生无穷奇数次谐波电压，而在环流中产生无穷偶次谐波电流。但这些奇次谐波电容电压及偶次谐波环流是依次递减的，一般可以忽略五次以上谐波电压及六次以上谐波环流。

由此可见，环流的偶次谐波的产生是互为因果，互相影响的，低偶次谐波产生了高偶次谐波，但高偶次谐波反过来又会影响低偶次谐波。电容 Cac的基波由负载电流及环流直流成分产生。三次谐波由环流二次谐波产生。

4.2 环流控制策略

如果只考虑环流的二次及四次谐波，假设三相输出电流按正序分布，则根据式（21）以及图2中的关系，三相环流的表达式可以写成

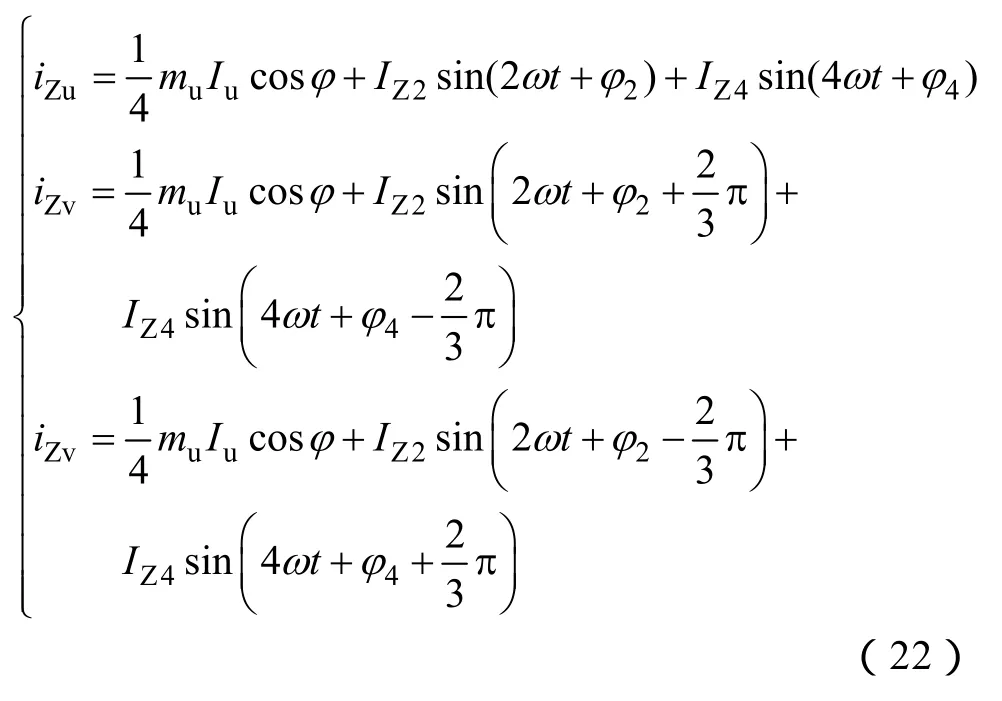
可见，环流的二次谐波按负序分布，四次谐波按正序分布。事实上，环流谐波以二次谐波为主导，为此可以通过坐标变换将式（22）变换到负序两倍基波频率坐标系中，可得

式（23）中，前两个方程为三相环流在负序两倍频基波频率坐标系中的微分方程，此时，二次谐波环流表现为直流特性，四次谐波环流表现为六次谐波特性，式中 vT22d和 vT22q为式（19）中 2Suvac在dq坐标系中的分量，其同样含有直流分量和六次谐波分量。由此可见，在该 dq坐标系中，环流方程中含有直流分量和六次谐波分量。

式（23）中的第三个方程为环流的零序分量微分方程，体现了环流的直流特性，式中 vdc0为 vdc的直流分量。第四个方程为三相 vdc的零序分量微分方程，由于环流中含有二次谐波分量，则vdc中必然含有二次谐波分量，根据三相的对称性可知，三相vdc之和必然为直流分量。控制 iZ0就可以控制 vdc0的大小。式中ip0表示为

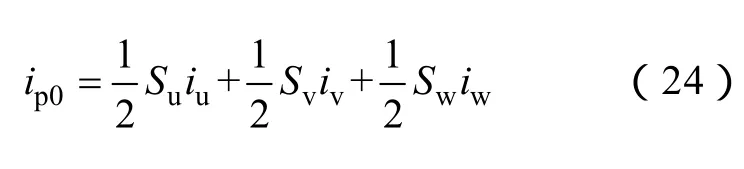
显然，ip0为直流分量，体现了输出功率的大小。

从式（9）和式（10）可知，在正、负桥臂中同时注入一个控制量可以实现对环流的控制而不影响输出电压。基于此，可以得到一种环流及电容电压的控制方案，如图3所示。图中控制系统分为两部分，第一部分为电容电压控制，其在零序坐标系中进行，vdc0和给定v*dc的差反映了对环流直流分量的需求，通过对环流直流分量的控制来控制电容电压的直流成分，图中引入ip0进行前馈控制用于提高系统响应速度；第二部分为环流谐波抑制，通过坐标变换把三相环流变换到负序两倍频坐标系中，其dq分量除了直流成分外还有六次谐波分量，为了更好地抑制二次谐波环流，对文献[15]的策略进行改进，先通过LPF滤掉其中的六次谐波分量，使其仅剩下直流分量，通过解耦控制，将直流分量控制到零，这样就抑制了二次谐波环流。控制器得出的控制量经过反变换得到三相控制量，分别加在正、负桥臂的调制电压上，经过 PWM调制及电容均压策略控制所有模块的开关导通和截止。

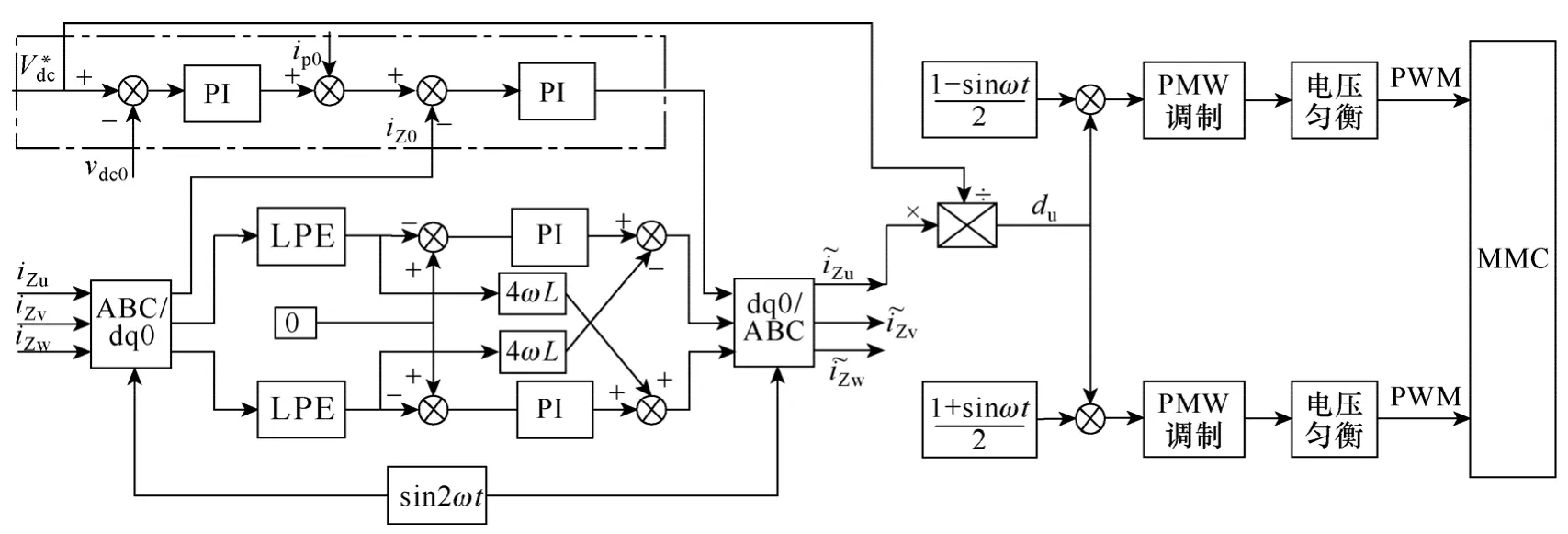
图3 系统控制框图Fig.3 The system control diagram

5 仿真及实验

5.1 仿真研究

为验证文中结论的正确性，搭建了一个每个桥臂 14个模块的三相 MMC系统，输入直流电压为14kV，具体参数见下表。采用载波层叠 SPWM 调制技术，载波频率为5kHz，输出相电压为15电平。

表 仿真参数Tab.Simulation parameters

图4所示为不加环流控制时的仿真波形，其中图4a和图4b为输出相电压及电流波形，输出电压有15电平，THD值约为4%，电流波形THD值为0.64%，基本实现了无谐波输出。图4c为u相输出电流和环流的波形，可以看出：环流除了直流分量外，还有明显的二次谐波成分。图4d为三相环流在负序两倍基波频率的dq0坐标系的波形，三个波形中都含有六次谐波分量，表明在环流中含有4次（4次谐波经过负序两倍基波频率变换后呈现为6次谐波特性）及6次谐波（6次谐波保留在环流的零序分量中）。图4e所示为电容电压vdc的波形，其反映了正、负桥臂所有电容电压和的一半，其平均值略小于输入的14kV，原因是存在桥臂等效电阻的分压作用。同时在 vdc中含有明显的二次谐波波动。图4f所示为 vac的波形，其反映了正、负桥臂电容电压之差，其明显含有基波及三次谐波。

图4 不加环流控制时的仿真波形Fig.4 The simulation waveforms without circulating current control

图5所示为文中提出的控制策略的仿真波形。动态仿真时，在0.2s和0.6s分别突然加上和切除负载。图5a所示为u相输出电流及环流的仿真波形，环流的低次谐波被消除，只含有直流及高次谐波成分，对输出电流没有影响。图5b所示为三相环流在dq0坐标系中的波形，其dq分量被控制到零附近，表明二次谐波已被消除，而零序分量被控制在所需的大小。图5c和图5d为vdc的仿真波形，图5d为稳态波形，其三相平均值被控制在14kV，二次谐波波动依然存在。图5c为vdc动态仿真波形，在0.2s，负载突加时，其平均值仍然被控制在 14kV，但三相波动并不平衡，因为电路的初始状态不一样，造成在控制初期三相电容获得的能量不同，经过一段时间后恢复平衡。0.6s负载切除后，电容电压在直流侧进行充、放电，其波动缓慢衰减至零。图5e和图5f为vac仿真波形，图5f为稳态波形，可以看出vac中的三次谐波被消除，只剩下基波，其原因是 vac的三次谐波是环流的二次谐波通过网络 T2的作用而产生的，当环流的二次谐波被消除后，vac的三次谐波自然就不存在了。图5e为vac的动态仿真波形，在负载突然加上和切除后，三相vac并不平衡，要经过一段时间的调整后才最终平衡。vac反映的是正、负桥臂电容电压之差，如果该差值变化太过剧烈就有可能影响系统的稳定，因此，在控制过程中必须关注vac的变化。

图5 加环流控制策略后的仿真波形Fig.5 The simulation waveforms with circulating current control

5.2 实验研究

为进一步验证文中结论，搭建了一个缩减版的实验平台，其输入直流为560V，每个桥臂4个模块，模块电容为 2 200μF，桥臂电感为 3mH，负载电阻为22Ω，负载电感为10mH，输出电平数为5，调制频率为 10kHz。控制器以 DSP和 FPGA为核心，FPGA负责控制波形产生以及电容电压的测量，而DSP则负责相关算法的执行。

图6所示为实验波形。图6a和图6b分别为三相输出电流和电压波形，输出电流为正弦，输出电压为5电平。图6c所示为不进行环流控制时u相输出电流和环流波形，环流中明显含有直流分量和二次谐波分量。图6d所示为进行环流控制时的波形，环流的低次谐波基本得到抑制。图6e和图6f分别为进行环流控制前后的vdc波形，其幅值波动甚至有所增大，因为影响vdc电压波动的因素有两个：一个是环流二次谐波，另外一个是负载电流通过T1的调制作用而产生的二次谐波电流，环流二次谐波被抑制后，影响vdc波动的只剩下后一种因素，在前一种情况下，有可能两个二次谐波电流叠加造成流入 Cdc的二次谐波电流减小，从而使vdc波动有所减小。图6g和图6h分别为环流控制前后vac的波形，vac的三次谐波得到了明显抑制。

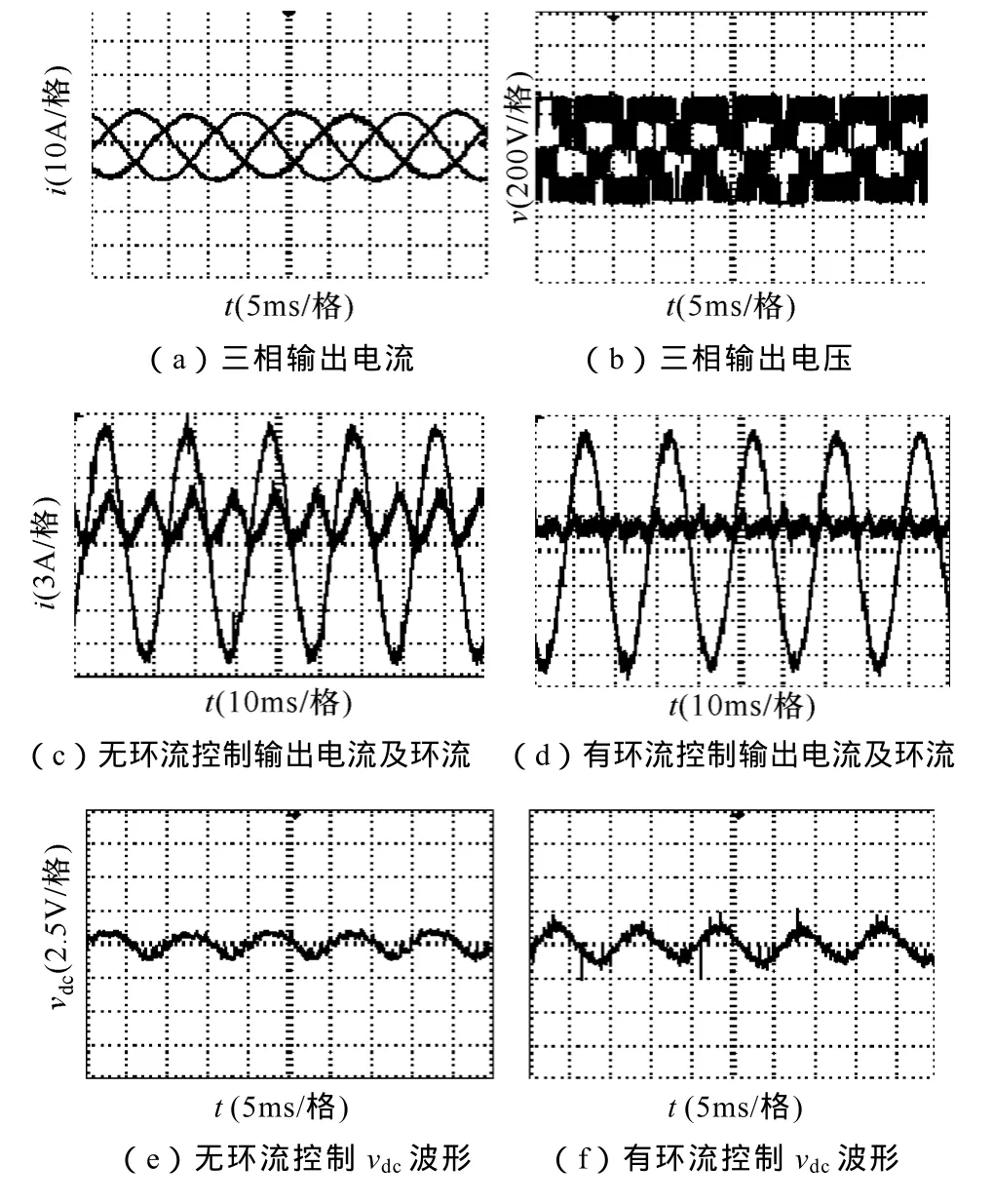
图6 实验波形Fig.6 The experimental waveforms

6 结论

本文建立了MMC系统的单相状态方程，利用该方程定性分析了环流及电容电压波动的谐波成分，指出环流中除了直流及二次谐波成分外，还含有其他偶次谐波。证实了三相环流二次谐波呈负序分布，推导出了三相状态方程在负序两倍基波频率的dq0坐标系中的形式，dq坐标系的方程反映了环流的谐波特性，零序分量的方程则反映了电容电压和环流的直流特性。在此基础上提出了环流谐波和直流分量分别独立控制的测量，改进了传统的有关环流谐波的抑制策略。仿真和实验证实了文中提出的策略和结论。为MMC系统的环流分析和控制提供了依据。

[1] Lesnicar A,Hildinger J,Marquardt R.Modulares strom-richterkonzept fur netzkupplungsanwendung bei hohen spannungen[C].ETG-Fachtagung,Bad Nauheim,Germany,2002,88: 155-161.

[2] Lesnicar A,Marquardt R.An innovative modular multilevel converter topology suitable for a wide power range[C].IEEE Power Technology Conference,Bologna,Italy,June 23-26,2003.

[3] Steffen Rohner,Steffen Bernet,Marc Hiller,et al.Modulation,losses,and semiconductor requirements of modular multilevel converters[J].IEEE Transactions on Industrial Electronics,2010,57(8): 2633-2642.

[4] 管敏渊,徐政.向无源网络供电的 MMC型直流输电系统建模与控制[J].电工技术学报,2013,28(2):255-263.Guan Minyuan,Xu Zheng.Modeling and control of modular multilevel converter based VSC-HVDC system connected to passive networks[J].Transactions of China Electrotechnical Society,2013,28(2): 255-263.

[5] Mohammadi H P,Tavakoli Bina M.A transformerless medium-voltage statcom topology based on extended modular multilevel converters[J].IEEE Transactions on Power Electronics,2011,26(5): 1534-1545.

[6] 杨晓峰,范文宝,王晓鹏,等.基于模块组合多电平变换器的STATCOM及其控制[J].电工技术学报,2011,26(8): 7-13.Yang Xiaofeng,Fan Wenbao,Wang Xiaopeng,et al.Static synchronous compensator based on modular multilevel converter based STATCOM and its control[J].Transactions of China Electrotechnical Society,2011,26(8): 7-13.

[7] 范文宝,杨晓峰,王晓鹏,等.基于模块组合多电平变换器的SVG控制策略[J].电工技术学报,2011,26(1): 29-35.Fan Wenbao,Yang Xiaofeng,Wang Xiaopeng,et al.Control strategy SVG based on of modular multilevel converter[J].Transactions of China Electrotechnical Society,2011,26(1): 29-35.

[8] Makoto Hagiwara,Kazutoshi Nishimura,Hirofumi Akagi.A medium-voltage motor drive with a modular multilevel PWM inverter[J].IEEE Transactions on Power Electronics,2010,25(7): 1786-1799.

[9] Makoto Hagiwara,Hirofumi Akagi.Control and experiment of pulse width-modulated modular multilevel converters[J].IEEE Transactions on Power Electronics,2009,24(7): 1737-1746.

[10] Makoto Hagiwara,Ryo Maeda,Hirofumi Akagi.Control and analysis of the modular multilevel cascade converter based on double-star chopper-cells(MMCC-DSCC)[J].IEEE Transactions on Power Electronics,2011,26(6): 1649-1658.

[11] Angquist L,Antonopoulos A,Siemaszko D,et al.Inner control of modular multilevel converters- an approach using open-loop estimation of stored energy[C].International Power Electronics Conference(IPEC),Sapporo,Japan,June 21-24,2010: 1579-1585.

[12] LennartÄngquist,Antonios Antonopoulos,Daniel Siemaszko,et al.Open-loop control of modular multilevel converters using estimation of stored energy[J].IEEE Transactions on Industry Applications,2011,47(6): 2516-2524.

[13] Antonopoulos A,Angquist L,Nee H P.On dynamics and voltage control of the modular multilevel converter[C].In Proceedings of 13th European Conference onPower Electronics and Applications,2009: 1-10.

[14] Siemaszko D,Antonopoulos A,Ilves K,et al.Evaluation of control and modulation methods for modular multilevel converters[C].In Proceedings of International Power Electronics Conference,2010:746-753.

[15] Tu Qingrui,Xu Zheng,Xu Lie.Reduced Switchingfrequency modulation and circulating current supperssion for modular multilevel converters[J].IEEE Transactions on Power Delivery,2011,26(3): 2009-2017.

[16] 孙世贤,田杰.适合 MMC型直流输电的灵活逼近调制策略[J].中国电机工程学报,2012,32(28):62-67.Sun Shixian,Tian Jie.Flexible approach modulation strategy for HVDC based on modular multilevel converter[J].Proceedings of the CSEE,2012,32(28):62-67.

[17] 王晓鹏,杨晓峰,等.模块组合多电平变换器的脉冲调制方案对比[J].电工技术学报,2011,26(5):28-33.Wang Xiaopeng,Yang Xiaofeng,et al.A comparative study of multi-pulse modulation schemes for modular multilevel converters[J].Transactions of China Electrotechnical Society,2011,26(5): 28-33.

[18] 李笑倩,宋强,刘文华,等.采用载波移相调制的模块化多电平换流器电容电压平衡控制[J].中国电机工程学报,2012,32(9): 49-55.Li Xiaoqian,Song Qiang,Liu Wenhua,et al.Capacitor voltage balancing control by using carrier phase-shift modulation of modular multilevel converters[J].Proceedings of the CSEE,2012,32(9): 49-55.