基于零序电压注入与调制波分解的三电平脉宽调制策略
2014-06-22谢路耀金新民吴学智尹靖元童亦斌
谢路耀 金新民 吴学智 尹靖元 童亦斌
(1.浙江工业大学信息工程学院 杭州 310023 2.北京交通大学新能源研究所 北京 100044)
1 引言
总结近年风电行业发展态势,一方面海上风能发展提速,风机功率大型化趋势明显;另一方面,并网质量与可靠性要求提高,低谐波与电网故障穿越等风机并网标准越来越严苛[1]。而采用高压电力电子器件与多电平技术的中压全功率风电变流器,在降低单位容量造价、提高并网电流质量和电网故障穿越性能上优势明显,成为大型风机的完美解决方案[2]。在众多的多电平拓扑中,NPC(neutral point clamped)三电平拓扑(见图1),控制简单、器件数目小,具有最为广泛的工业应用。相对于两电平变流器,其优点有:①功率器件承受电压减小至直流母线电压的一半;②输出电压 du/dt减小一半;③相同开关频率下输出波形质量远优于两电平[3]。
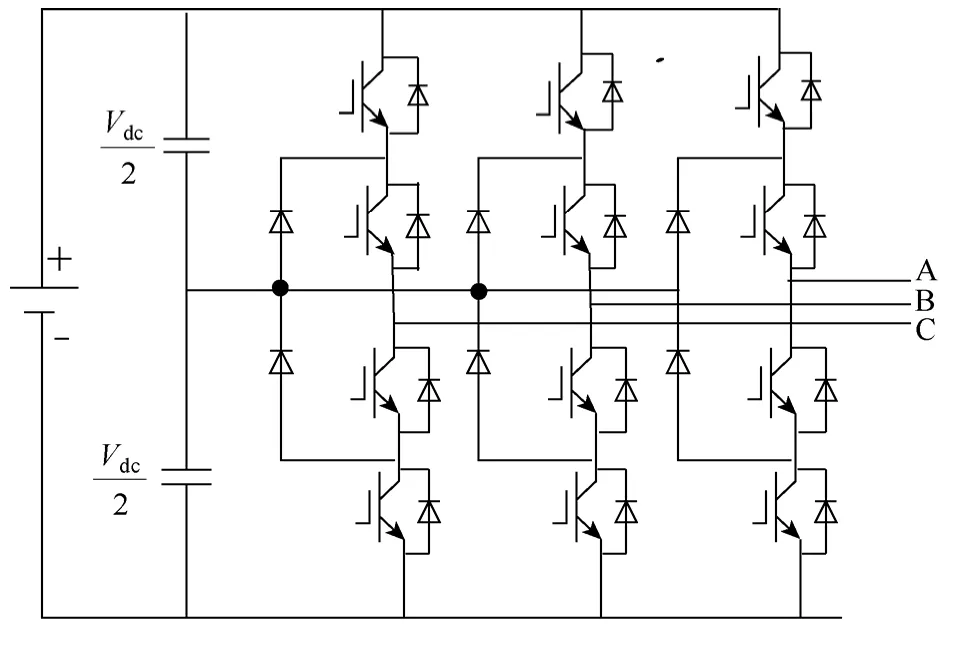
图1 NPC三电平拓扑结构Fig.1 The topology of NPC three-level converter
目前主流的 NPC三电平控制策略包括基于零序注入的SPWM与SVPWM两种,它们的特点是:
(1)基于零序注入的 SPWM:将注入零序分量的正弦调制波与平移的三角载波进行比较,生成对应的开关管脉冲[4]。此种方式的特点是实现简单,且注入合适的零序分量使中间矢量居中后,可以等效实现传统七段式(Nearest Three Vectors,N3V)SVPWM[5,6]。通过注入零序分量也可以实现对中点电位的控制,但由于无法准确判定叠加零序分量后相压的正负,使零序分量的计算方法过于复杂[7-9]。且在高调制系数、低功率因数下,此方法仍然无法实现开关周期内平均中点电流为零[9]。
(2)SVPWM:将三相电压在 αβ坐标系下用一旋转的参考矢量等效,按矢量分解原理和参考矢量的位置将其分解为附近几个开关矢量并制定其持续时间,使几个开关矢量在开关周期内的协同作用效果和参考矢量的作用效果相同[10]。SVPWM需复杂的扇区判定与矢量分解计算,优点是物理意义明晰,便于对调制策略进行解析与优化。因此,早期较深入的中点平衡分析[11]和具优良性能的中点平衡控制方式[12]都基于SVPWM展开。此外,通过优化的扇区划分、矢量序列选择和冗余小矢量配比可实现降低开关频率、提高波形质量[5,6]甚至在开关周期内实现平均中点电流为零[13]等优化控制目标。
应用于大功率风电并网变流器的 NPC三电平控制策略,必须兼顾并网电流质量和个别极端情况下的中点电位平衡控制。特别是在电网不对称跌落时,变流器三相电流不对称,在网压恢复期间又必须对电网进行无功支撑,功率因数低、三相不对称等恶劣工况对中点电位的平衡控制提出了严峻考验。在调制策略的选择上,采用不同的SVPWM调制策略确实可以解决上述复杂问题,但就实现方式来说,多种SVPWM在相互转化上存在扇区重新划分、矢量再次分解和开关序列表重新排序等问题,这些都使调制策略变得异常复杂。
为解决上述困难,本文提出了一种基于零序注入与调制波分解的三电平控制策略,其实现简单,可等效实现多种SVPWM的控制效果,并可在几种SVPWM控制效果间平滑转换,是风电变流器等需要多目标控制三电平变流装置的完美解决方案。
2 SVPWM与零序电压注入SPWM的一致性分析
2.1 零序注入型SPWM与SVPWM的宏观一致性
零序注入型 SPWM 虽然是一种基于相电压的调制方式,但零序分量对输出线电压不会产生影响,因此一个开关周期内,线电压的伏秒积与未注入零序分量前相等。
为了分析SVPWM是否具有同样的本质,将三相线电压定义为参考矢量,其表达式为
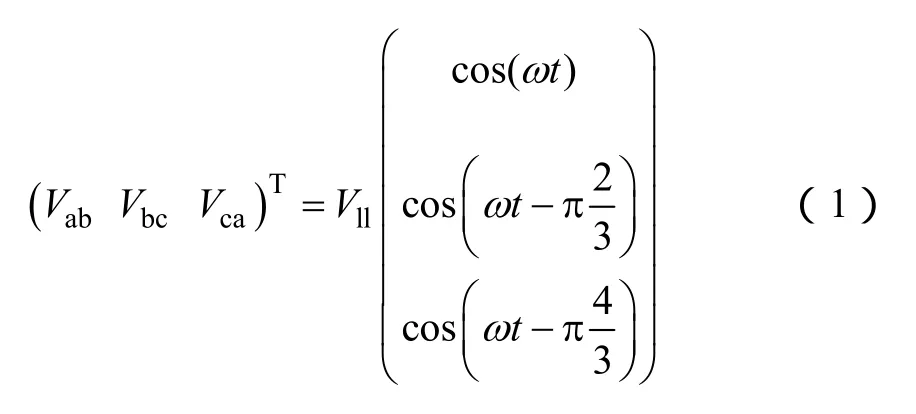
式中,Vll为线电压幅值。
将所有线电压表示的开关状态定位作图,可以得到三维空间的矢量图如图2所示。
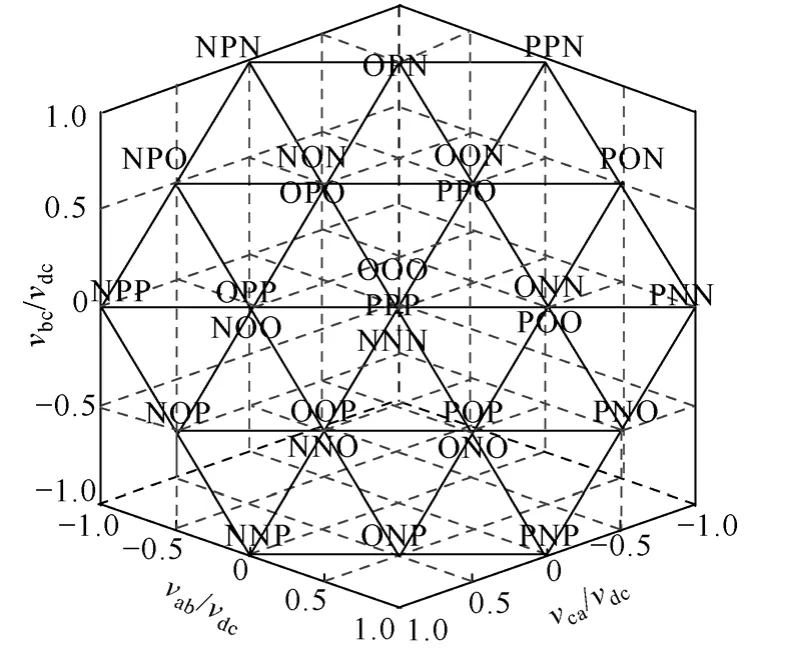
图2 线电压表示的三维三电平空间矢量图Fig.2 Line voltage based 3D three level space vector diagram
由于三相线电压之和为 0,任意以线电压表示的参考矢量Vref都位于图2的六边形平面上。比较图2与传统SVPWM三电平空间矢量图可以发现,不论是形状还是开关矢量的分布都一模一样,且图2基于线电压坐标系的参考矢量与传统SVPWM矢量图基于αβ坐标系的参考矢量有唯一对应关系
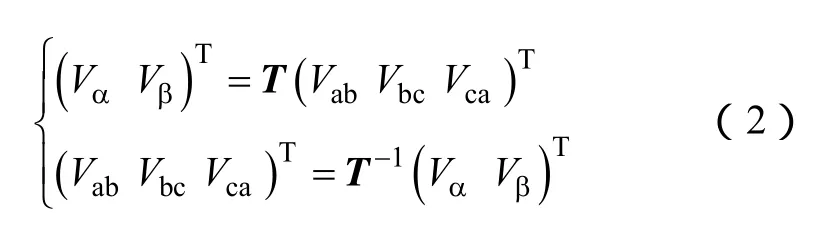
式中
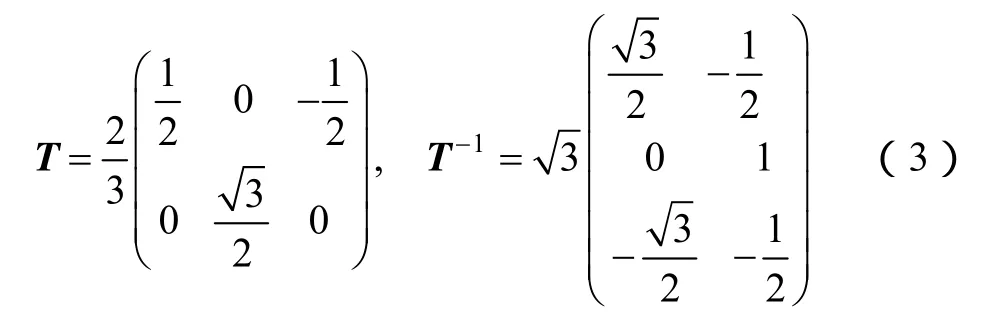
假设参考矢量Vref由V1、V2、…、Vn这n个开关矢量合成,则由SVPWM的矢量分解关系式
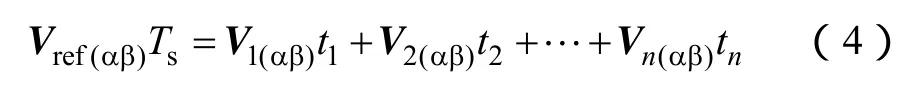
联系式(2)可以得到等效关系式
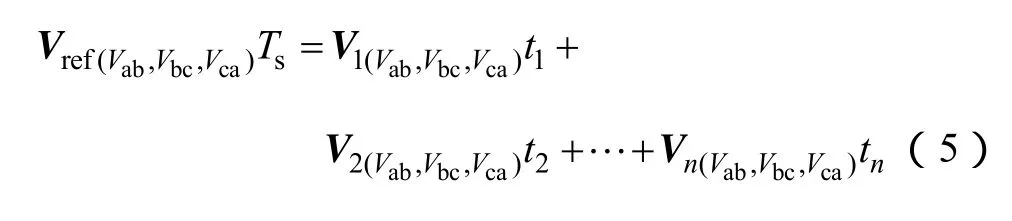
即
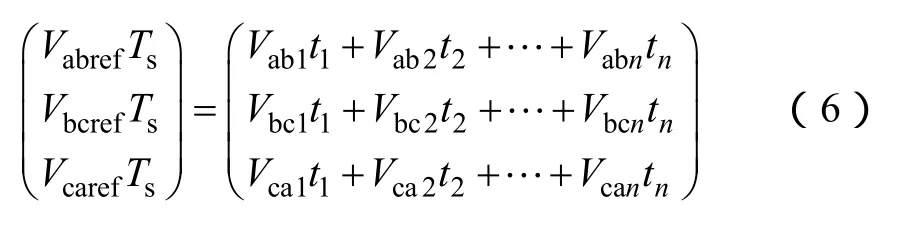
从式(6)得到,三电平 SVPWM 与零序注入SPWM在宏观本质上是相同的,都是在一个开关周期内基于线电压伏秒积相等的调制方式,在SPWM调制中注入零序分量并不会改变矢量在SVPWM矢量图中的位置。
2.2 零序注入SPWM与SVPWM的微观关系
本节将探讨在一个开关周期内,零序注入SPWM与SVPWM在扇区划分、开关序列排布、冗余矢量分配等方面的微观联系。
根据上一小节中讨论的结果,利用式(2)、式(3)表述的数量关系,可以在传统 SVPWM 矢量图中添加线电压坐标,如图3所示。线电压坐标系的添加使SVPWM与零序注入SPWM两种调制方式的联系更直观,αβ坐标系下的参考电压矢量在各线电压坐标轴上的投影放大倍后即为该相线电压的瞬时值。根据 Vref在各扇区所表示的相电压的相对大小,图3中将相电压分为最大、最小和中间值,依次以 Vmax、Vmin和 Vmid来表示。根据图3和各线电压关系,小扇区的判定可以用表1来表示。
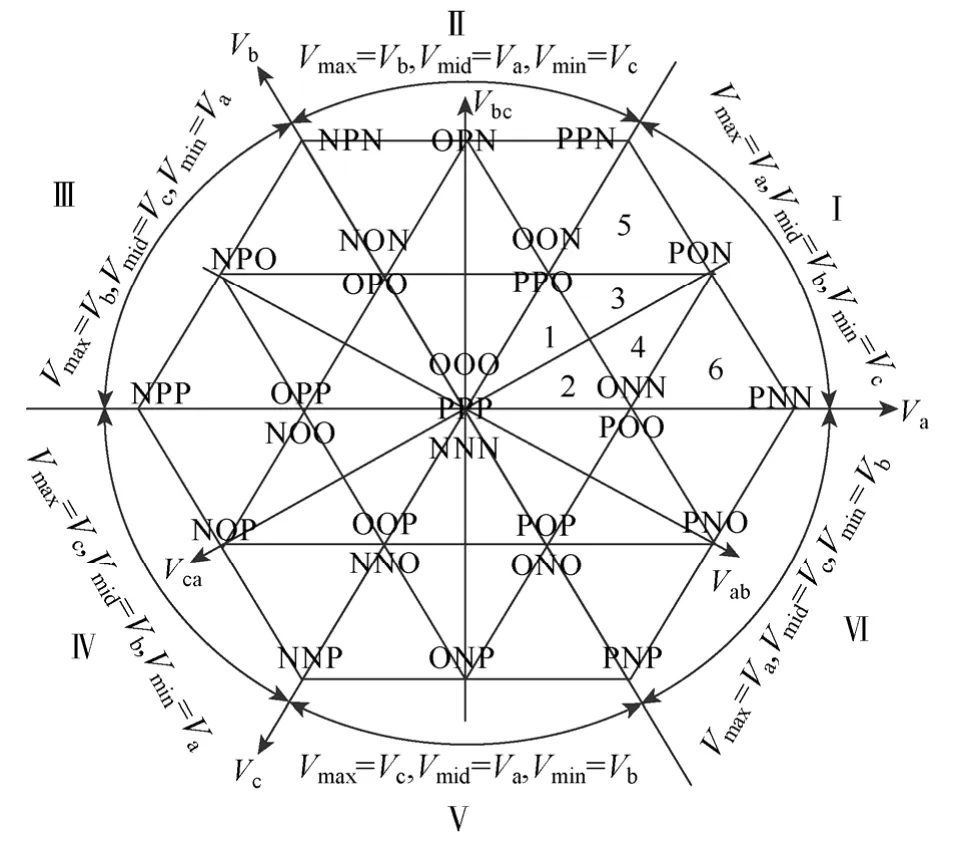
图3 三电平空间矢量图Fig.3 Three-level space vector diagram
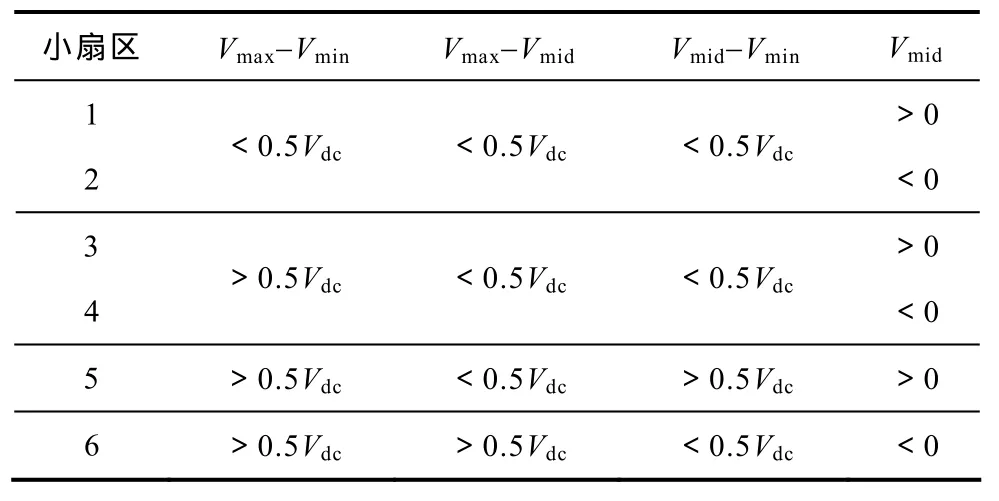
表1 小扇区判定表Tab.1 Small sector decision table
在零序注入 SPWM 中,为提高直流电压利用率,需将三相调制波电压限制在[-0.5Vdc0.5Vdc]范围内,为此文献[5,6]中首先注入零序电压分量
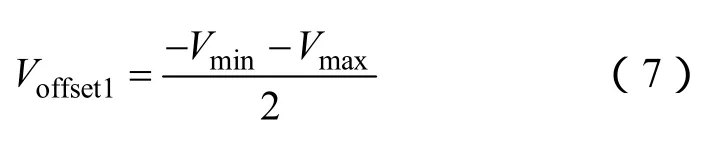
叠加Voffset1后,新的调制波为
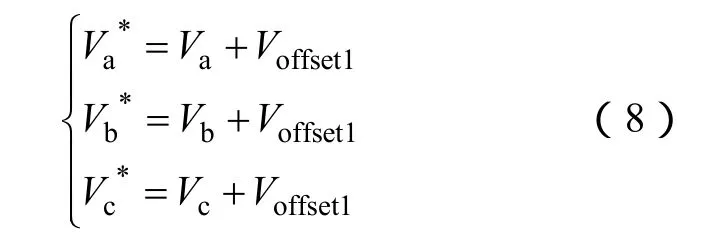
不难发现,叠加 Voffset1其实是对三相调制波进行了居中处理,新的三相调制波如图4所示,也依大小分为,有以下关系
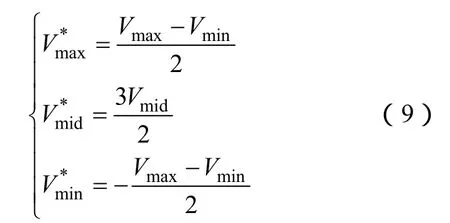
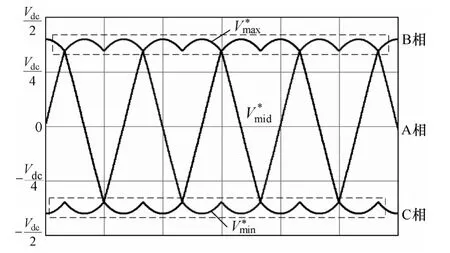
图4 叠加Voffset1后的三相调制波波形Fig.4 Three phase modulation waveforms injected with Voffset1
由三相调制波必须在[-0.5Vdc0.5Vdc]范围内,可以得到可继续叠加的零序分量Voffset2的范围
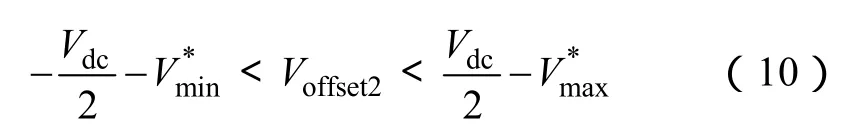
将三相调制波分解为 Vmax、Vmin和 Vmid后,对各大扇区的工况分析将完全一致,为节省篇幅,本文仅对大扇区Ⅰ(见图5)下每个小扇区一个开关周期内的开关序列分情况进行讨论。
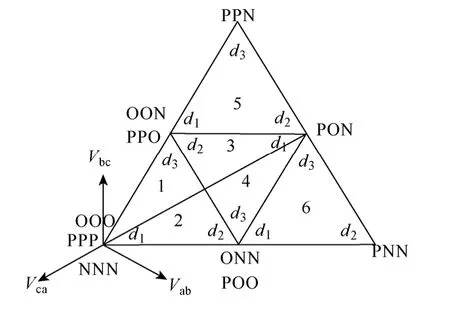
图5 大扇区Ⅰ的空间矢量图Fig.5 Space vector diagram in big sectorⅠ
根据式(6),并令0.5Vdc为满占空比,即

可以计算得到SVPWM调制下图5中各小扇区的占空比dn见表2。

表2 大扇区Ⅰ中各矢量的占空比Tab.2 Duty circle of each vector in sectorⅠ
文献[4]描述了一种基于载波平移的多电平SPWM调制方法,本文提出的三电平控制策略也将使用此调制方式为基础。根据式(8)得到的三相调制波和表1,绘制载波平移的SPWM在一个开关周期内的矢量序列如图6所示。从图6中三相调制波的相对位置可以得到,不需要任何计算,零序注入SPWM的各矢量占空比就天然满足表2中SVPWM计算得到的占空比,说明零序注入SPWM的线电压关系和 SVPWM的矢量分解完全等效。Voffset2的注入将使三相调制波上下平移,平移对矢量序列和占空比分布的影响可以用图7解释,虚线框为一个开关周期的长度,当前虚线框所处的位置为图6所对应的脉宽序列,叠加Voffset2将使虚线框左右移动,引起开关周期内矢量序列与占空比的改变,但无论如何移动,表2的占空比关系恒成立,改变的仅仅是冗余矢量及其配比。
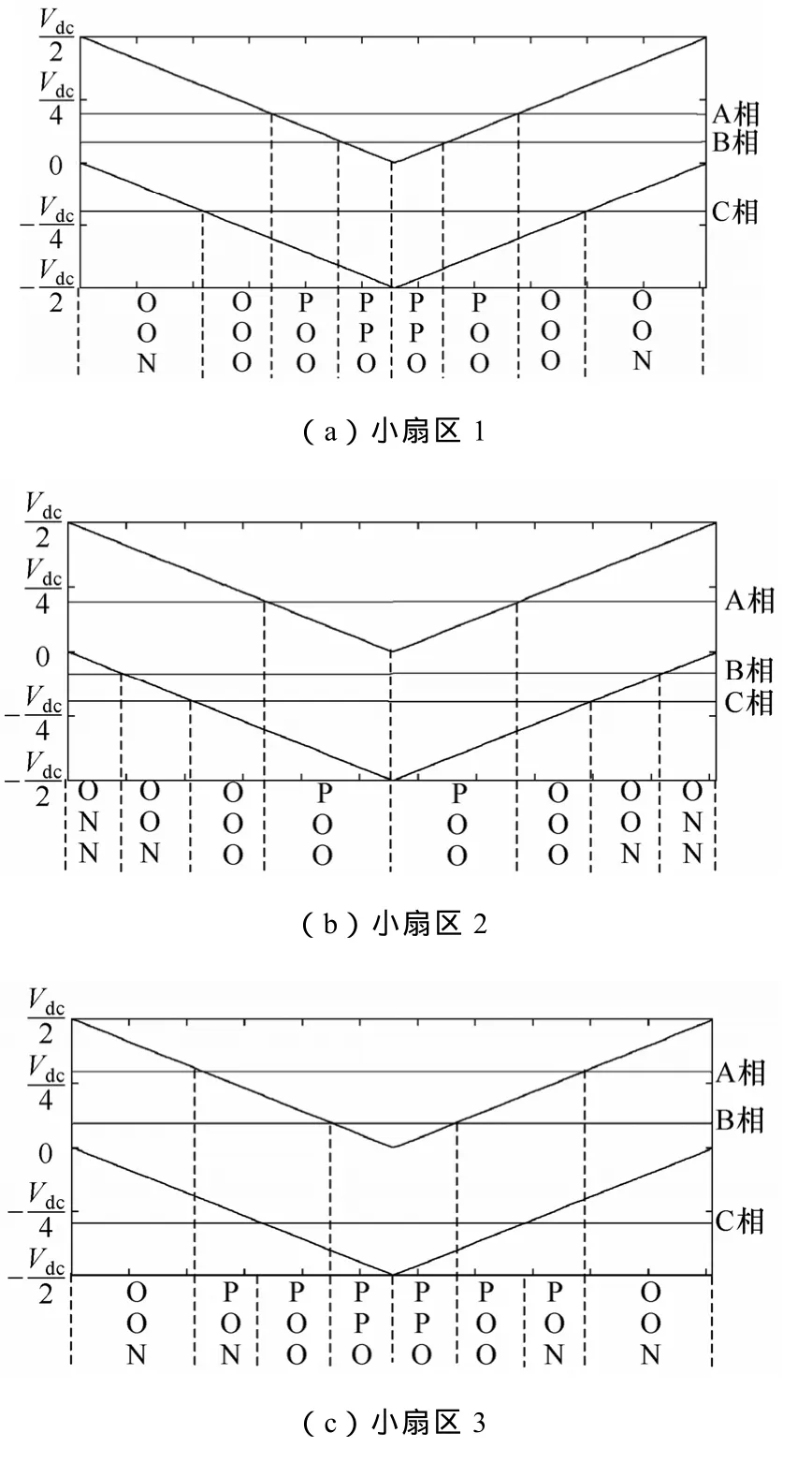
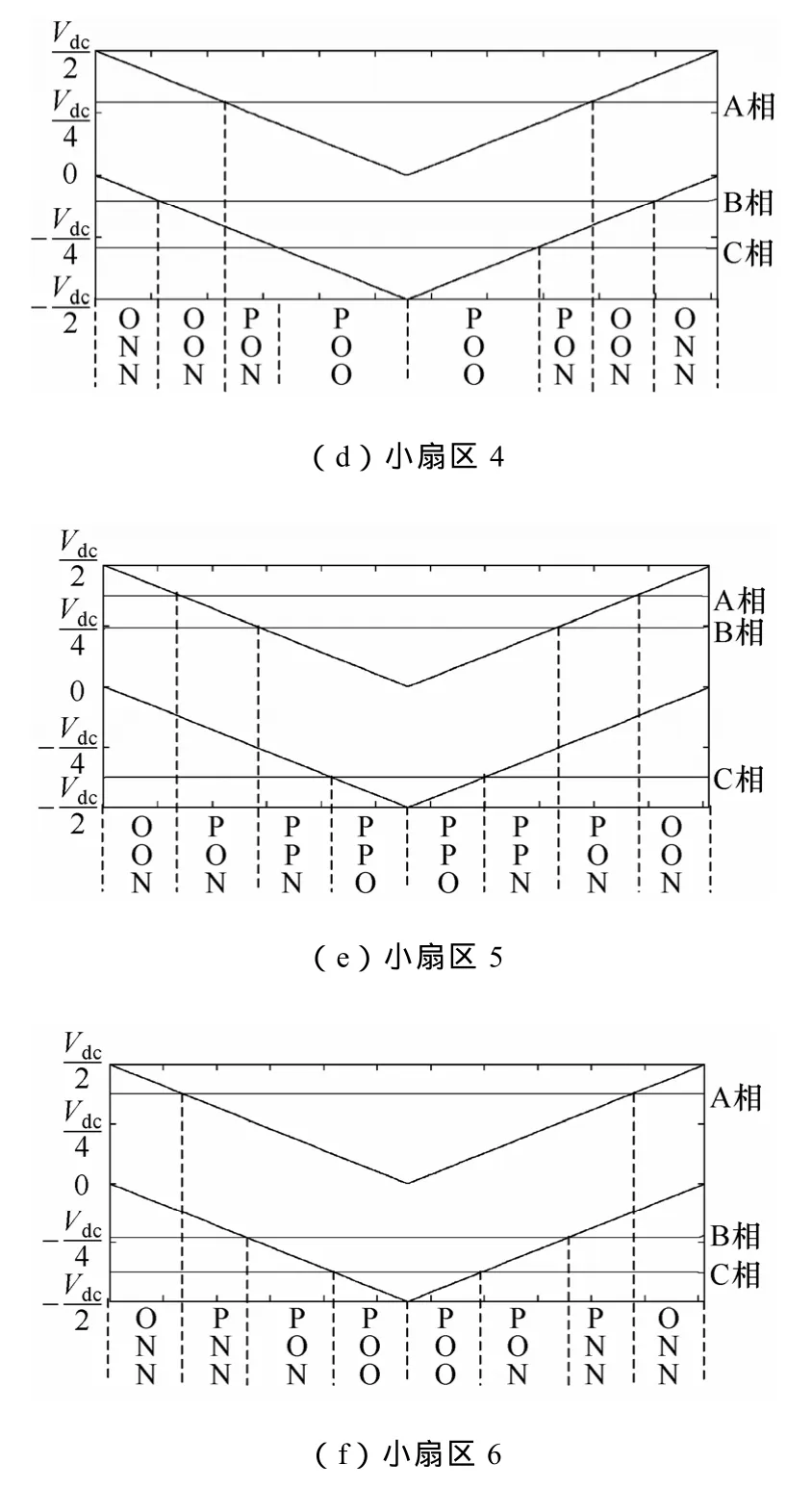
图6 大扇区Ⅰ中的三相调制波与矢量序列Fig.6 Three phase modulation waveforms and vector sequences in big sectorⅠ
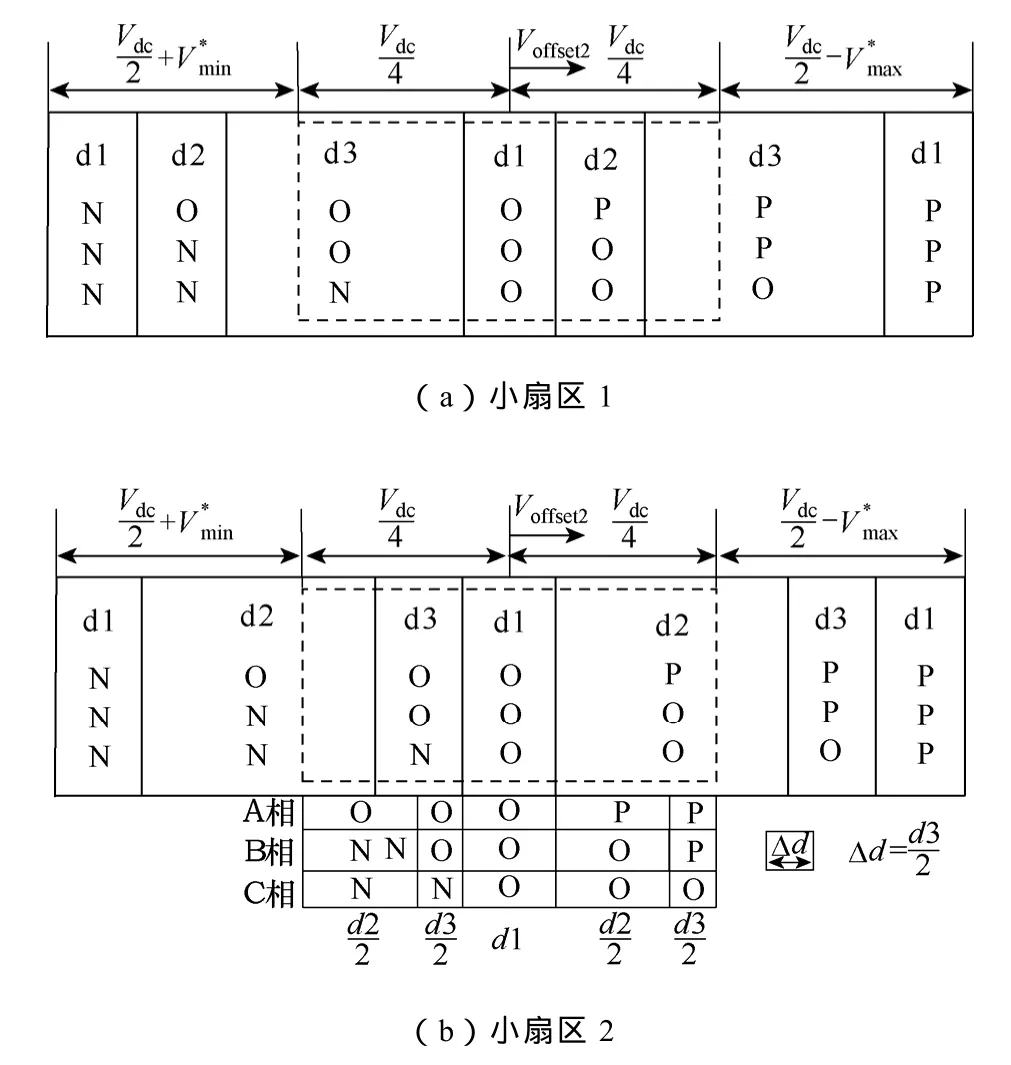
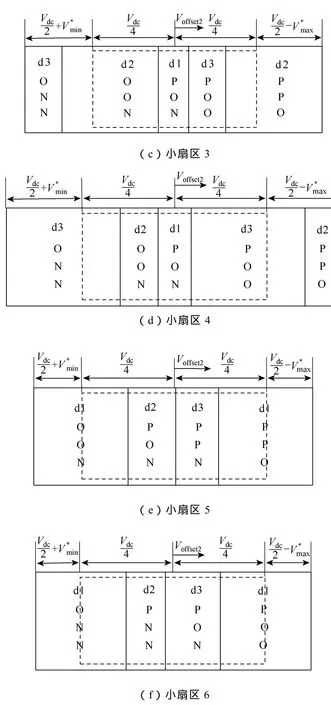
图7 开关周期窗口移动图Fig.7 Switching period window shift diagram
2.3 调制波的分解
无论虚线框如何移动,一个开关周期内每相桥臂至多只开关一次,因此通过零序注入,只能得到传统五段式或七段式N3V的调制方法。若想得到更多的扇区分解方法与矢量序列组合,在零序电压注入后,还须将调制波进行正负分解。分解后的正调制波Vx+和负调制波Vx-为
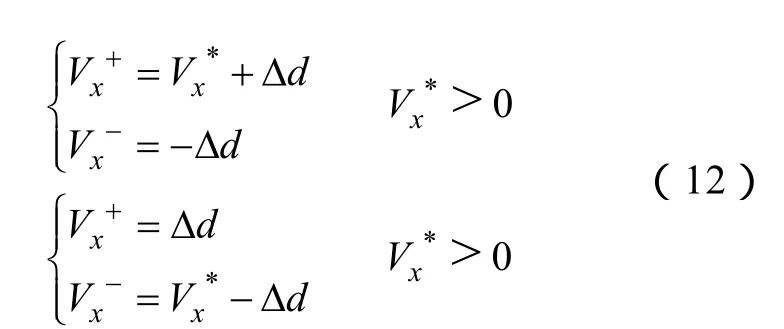
参见图7b对B相的分解,调制波的分解使开关序列的首末分别叠加了占空比同为Δd的N和P序列,等效于SVPWM调制方式中扇区划分和冗余矢量分配的变化,但对该相调制波的平均幅值没有丝毫影响,当然也不会破坏线电压伏秒积的平衡关系。随着Δd的增大,三电平桥臂将趋于PN转变的两电平工况,开关过程容易出现器件端压超过0.5Vdc的情况,因此,必须在PN状态之间叠加一个最小的O状态VminO,Δd的最大值也由此计算得到。
3 基于零序注入与调制波分解的脉宽调制策略的目标优化控制
3.1 最小开关损耗
减小开关损耗,就是使某相在一个开关周期内的矢量序列不变化,也就是通过叠加零序使某相调制波等于0或±0.5Vdc。从图7发现,通过叠加合适的零序分量,在1、2、3、4小扇区可以使任意相桥臂不开关,而在 5、6小扇区只能使相压为 Vmax与Vmin的两相桥臂不开关。其中,在1、2扇区,Vmax与Vmin相既可以等于0也可以等于±0.5Vdc,但等于±0.5Vdc的情况可能使两个相邻周期出现P、N变化,因此,只能使其等于 0。综上所述,在各扇区要使各相不开关所需叠加的Voffset2为

扇区判定依表1进行,为了最大限度降低开关损耗,还可对三相电流实时值进行比较,选择让电流幅值最大的相不开关。
3.2 优化波形质量
为了优化输出电压的波形质量,需要满足两个条件[5,6]:①采用 N3V的调制方法;②满足最优矢量序列的排布原则:非冗余矢量居中,冗余矢量均分并依次排布在序列的首末。
按照规则,对于传统七段式N3V,Voffset2为[5,6]
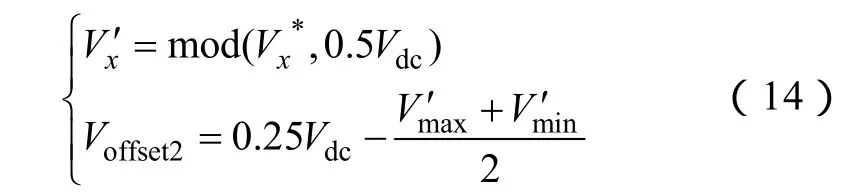
使用本文中调制波分解的方法,可以达到比七段式 N3V更优的波形质量。分析虚线框内的开关周期,在1~4区,的注入已将OOO或PON居中,进一步把相分解,可以在开关序列的始或末添加一个冗余矢量,使一个开关周期内伏秒积的波动更小。以图7b为例,取30.5d d Δ = ,序列末增加了PPO,并使矢量序列满足了最优波形质量的两条规则。在5、6扇区,最优波形质量的规则已被满足,对相的分解反而将使调制方式脱离N3V的原则。扇区判定依表1进行,总结1~6区达到最优波形质量所需的Δd有以下关系

3.3 中点电压平衡
注入Voffset1后的三相调制波,对相进行调制波分解,其流入中点的平均电流Inpav的表达式可以写为
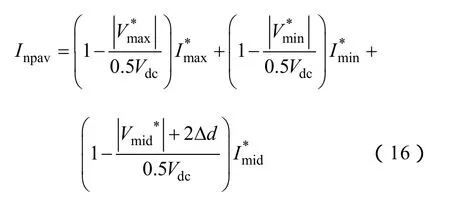
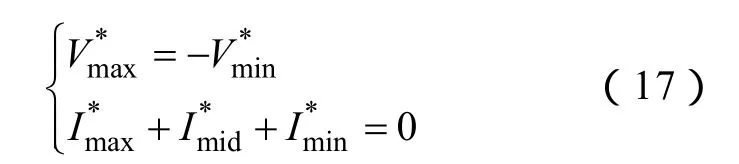
可以得到平均中点电流的简化式
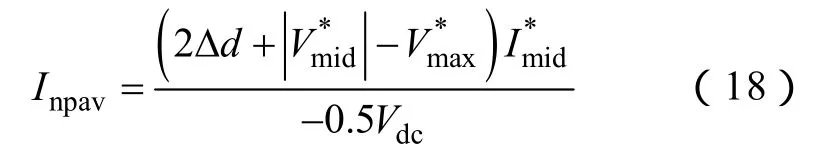
假设上、下电容不平衡电压差为ΔV,上、下组电容的容值为C,开关频率为f,若在一个开关周期内需要补偿不平衡电压,即
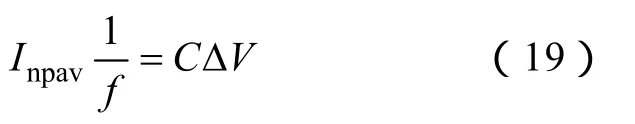
代入式(18)得
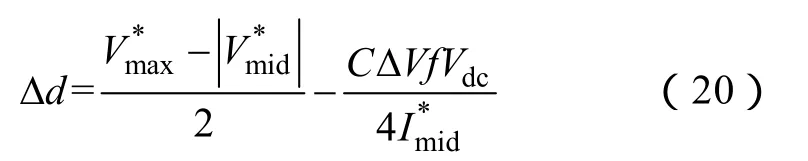
若ΔV为0,上式为
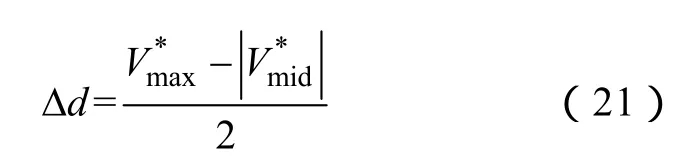
式(20)需要满足式(12)中Δd的约束条件,当计算得到的Δd超限时,需按边界值选取。式(20)说明,在全功率因数和调制比范围,仅需检测实时相电流和不平衡电压,就可以通过分解相,对中点电压进行平衡控制。式(21)说明,当中点电位恢复平衡后,必然存在 Δd使一个开关周期内的平均中点电流为零,达到消除中点电位低频波动的目的。文献[13]中讨论的基于虚拟矢量的中点平衡控制方法,其实就是式(21)的特例,与文献[13]相比,本文的中点平衡控制方法免去了繁琐的扇区划分与矢量计算,还可以对中点电位进行反馈控制,方式更简便性能更优异。
4 仿真结果
4.1 最小开关损耗的三电平调制
使用式(13),根据三相电流的大小,进行最小开关损耗三电平调制,在各调制比与功率因数下得到的波形如图8所示。可以得到,在功率因数较高与调制比较低时,可在电流为峰值时完全实现无开关损耗;但当调制比较高且功率因数较低时,由于相电流最大的相正好为V*mid相,且其位于5、6区,式(13)最小开关的条件无法成立,如图8d的A、B区域。在这种情况下,可以优化使电流幅值第二大的相进行最小开关损耗控制。
4.2 优化波形质量的三电平调制
使用式(14)和式(15),可以得到最优波形质量的传统七段式 N3V调制和本文双调制波调制在各调制比下的三电平输出电压波形与FFT分析如图9。高调制比时,两种调制方式的波形与谐波分布基本相同,这是因为式(14)、式(15)在5、6区其实相等;在调制比较低时,虽然总THD两种调制方式相当,双调制波调制略低,但谐波的分布上,双调制波调制的谐波集中分布在开关频率及其倍次上,在滤波器的设计上更简单且易取得更好的滤波效果。
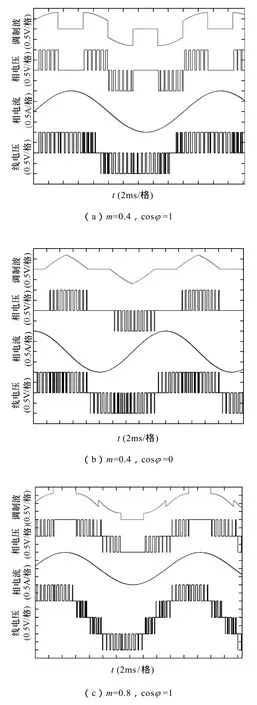
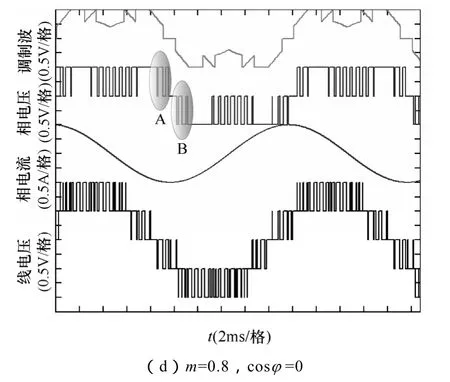
图8 最小开关损耗三电平调制(基波50Hz,开关频率1 800Hz,各变量标幺化为1)Fig.8 Minimum switching loss three-level modulation(Fundamental=50Hz,Switching frequency=1 800Hz,all variables are in pu)
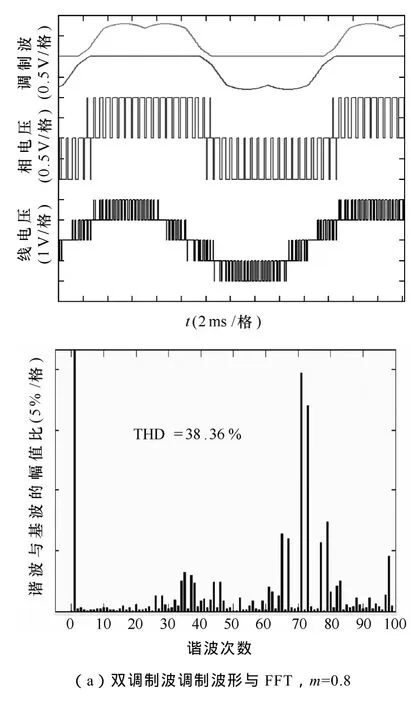
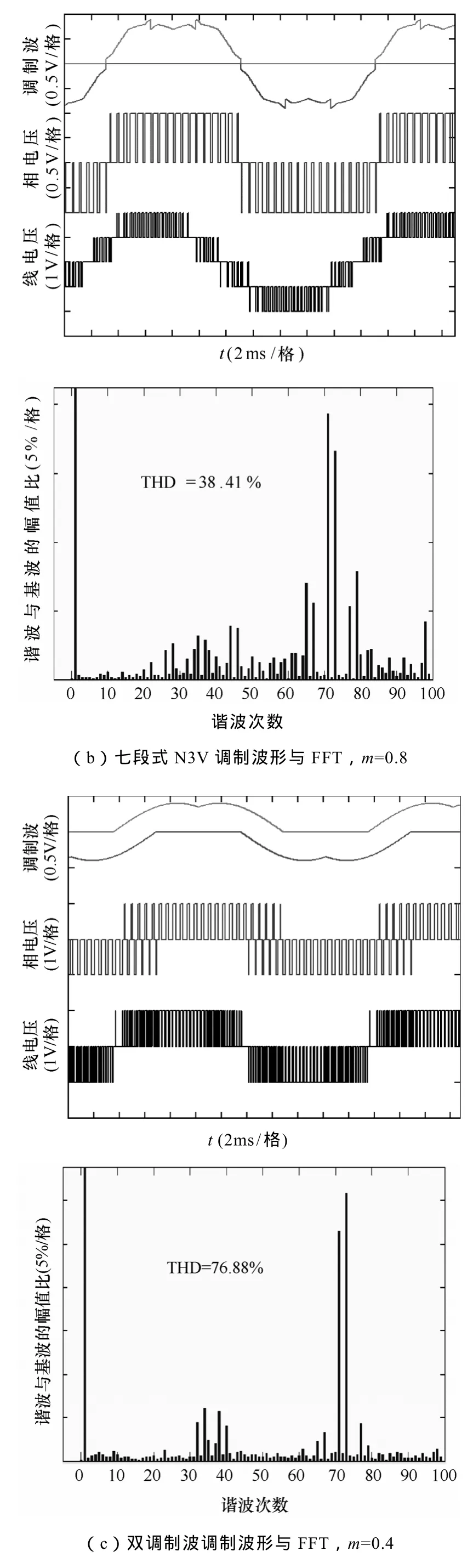
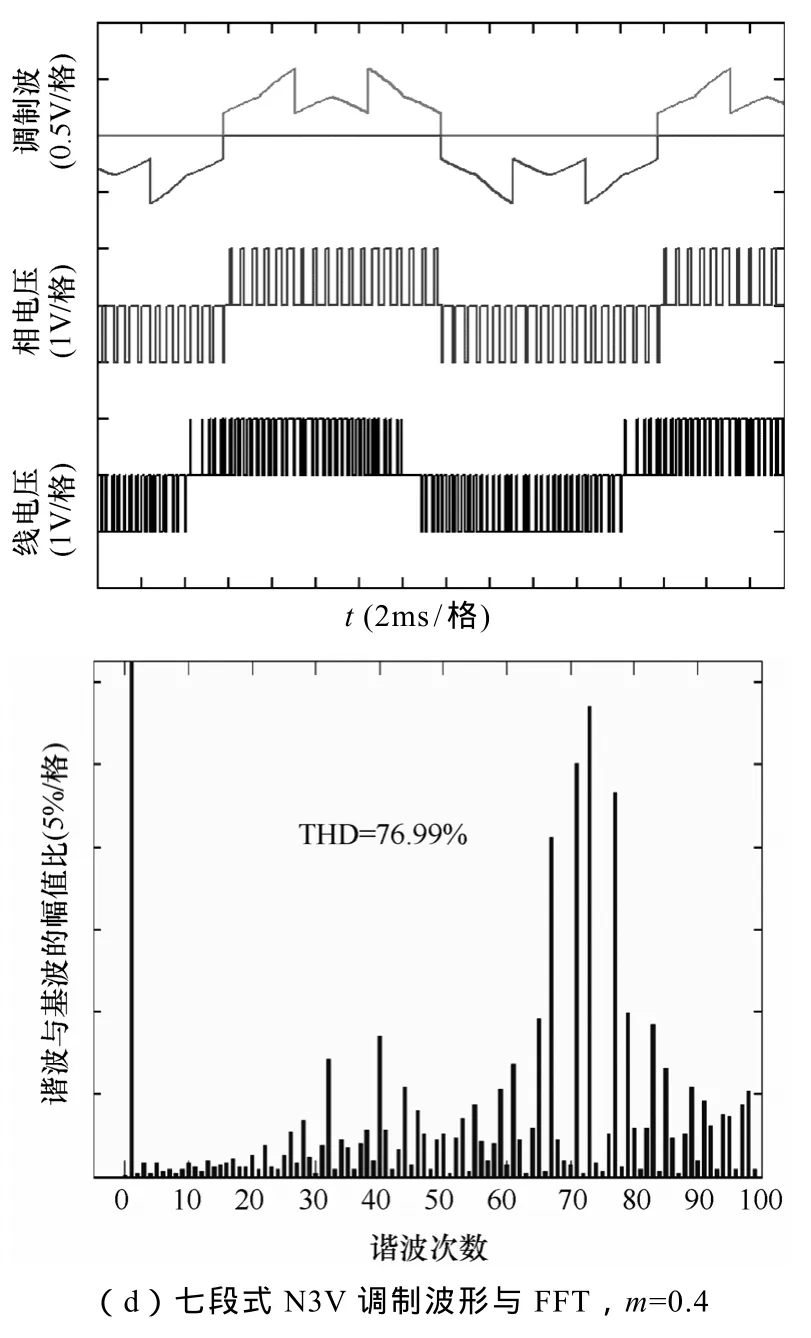
图9 最优波形质量三电平调制(基波50Hz,开关频率1 800Hz,各变量标幺化为1)Fig.9 Optimal waveforms quality three-level modulation(fundamental=50Hz,switching frequency=1 800Hz,all variables are in pu)
4.3 双调制波中点平衡调制
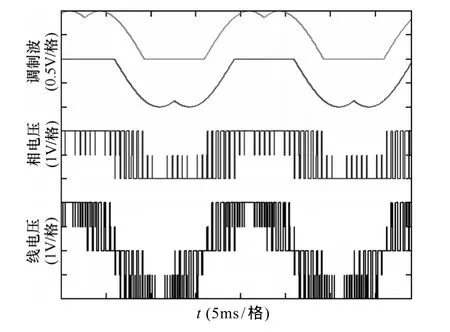
图10 双调制波中点平衡三电平调制(基波50Hz,m=1,开关频率1 800Hz,各变量标幺化为1)Fig.10 Double modulation waves three-level modulation with neutral point balance(fundamental=50Hz,switching frequency=1 800Hz,all variables are in pu)
使用式(20),可以得到双调制波中点平衡调制的波形如图10所示。和最优波形质量的双调制波相比,中点平衡的三电平调制不是基于N3V的调制方式,在5、6区调制波也进行了分解。不同调制方式的中点平衡控制效果见图11,图中前20ms为传统七段式N3V调制,20~40ms在N3V调制中加入了中点平衡控制,40ms以后为双调制波中点平衡调制。图中纵坐标为中点波动系数 k,数值上等于相电流1A、对称组直流电容1mF、基波频率50Hz时的中点电位波动值。实际中点波动电压 ΔV可以将k、对称组直流电容容值C(mF)、基波频率f以及相电流幅值I代入下式得到

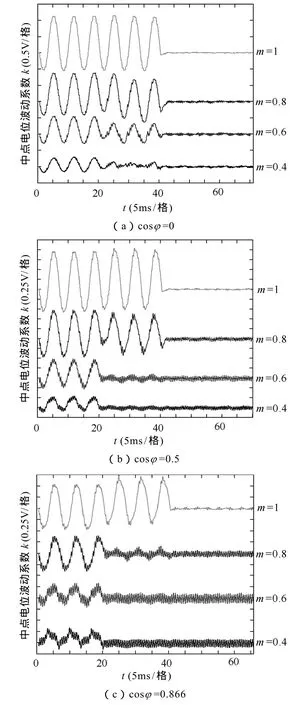
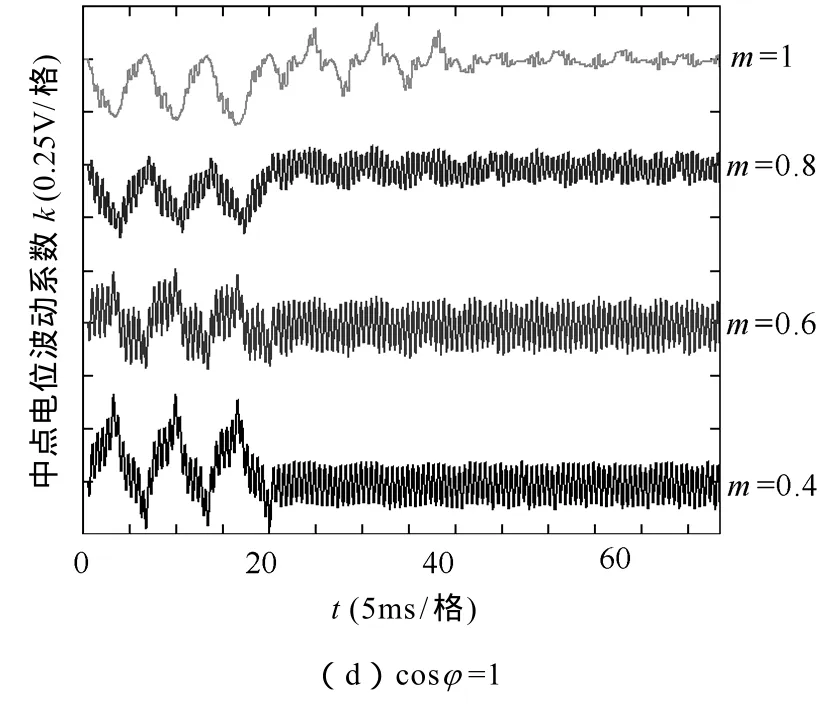
图11 各功率因数下中点平衡控制效果对比(基波50Hz,开关频率1 800Hz)Fig.11 Neutral point balance control performance contrast in different power factors(Fundamental=50Hz,Switching frequency=1 800Hz)
图11中,中点不平衡电压呈三倍基频振荡,调制比m越接近于1,功率因数cosφ越接近于0,振荡幅值越大,此时传统N3V的中点平衡控制效果已不理想,施加双调制波中点平衡调制后,中点电位的低频波动被完全消除。
5 实验结果
采用 DSP28335作为控制芯片,在交流阻感负载下对本文的调制策略进行了实验验证。实验条件基波 50Hz,开关频率 1 800Hz,对称组直流电容C=6.8mF,m=0.6,Vdc=125V,负载 L=1mH,R=1.7Ω,多种调制策略的切换和效果对比如图12所示,其中的正调制波经控制板DA转换得到,调制方式转换时相电流未出现波动,实现了平滑转换。
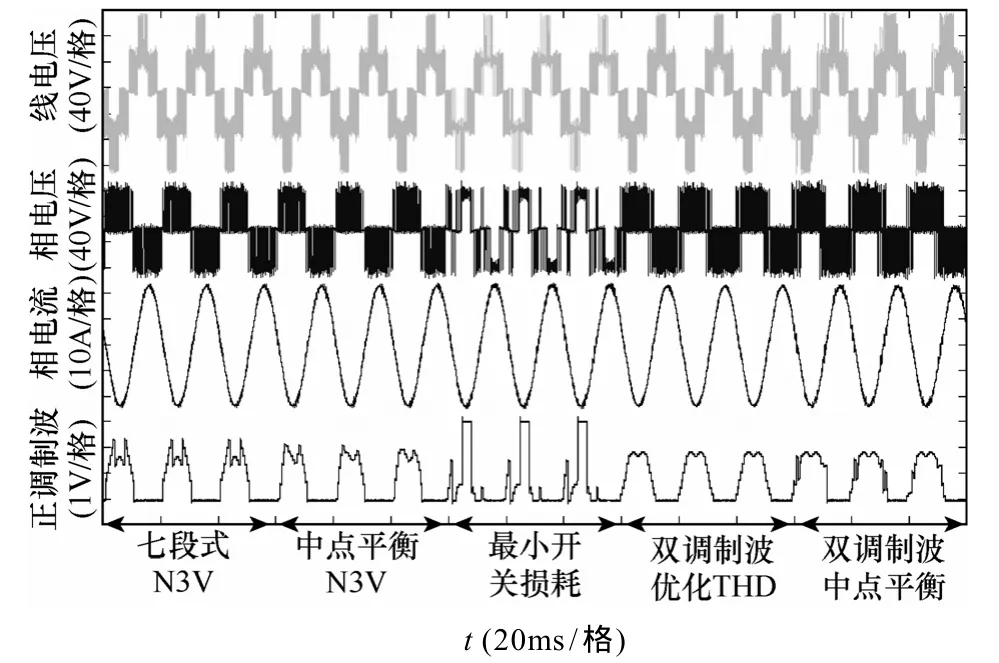
图12 多调制策略的切换和效果对比Fig.12 The switching and performance contrast of different modulation strategies
实验条件基波50Hz,开关频率1 800Hz,对称组直流电容 C=430μF,m=0.8,Vdc=125V,负载L=5mH,R=1.7Ω,多种调制策略的中点平衡效果对比如图13所示。最小开关损耗调制时未对中点电位偏移进行任何抑制,出现了较大波动;七段式N3V和双调制波优化THD两种调制方式,由于开关周期首尾的冗余矢量造成的中点偏移刚好互相抵消,仅非冗余矢量造成了中点的波动,中点电位波动情况得到了缓解;中点平衡N3V调制时波动得到抑制,但还是无法完全消除3倍基频波动(具体原因参见文献[11]);双调制波中点平衡调制实现了开关周期内平均中点电流为零,因此中点电位只存在高频波动,中点电位控制效果最好。
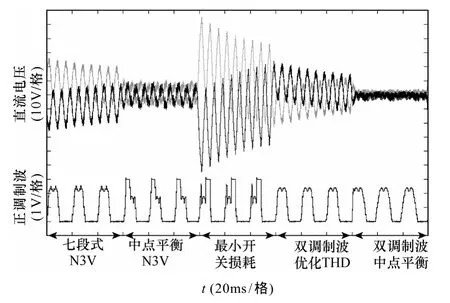
图13 多调制策略中点平衡效果对比Fig.13 Neutral point balance performance contrast in different modulation strategies
6 结论
(1)零序注入型SPWM与SVPWM三电平调制都是基于线电压伏秒积相等的调制方式,使用线电压坐标系空间矢量图和开关周期窗口移动图可以较为直观地解释两种调制方式在占空比和矢量序列上的一致性。
(2)注入零序电压使调制波等于±0.5Vdc或 0可以使该相不开关,通过检测相电流消除幅值较大相的开关损耗可以使整机开关损耗降至最低。
(3)将幅值居中的调制波分解,使非冗余矢量居中,冗余矢量对称首尾排布,可以优化输出线电压的谐波分布。
(4)检测实时相电流和中点不平衡电压,通过中间相调制波的分解,可以对中点电位进行反馈控制,并可在全范围消除中点电位的低频波动。
(5)所提出的基于零序注入与调制波分解的三电平调制方式,易于编程实现和控制目标转换,具有优良性能。
[1] 李俊峰、蔡丰波、唐文倩,等.风光无限2011中国风电发展报告[M].北京: 中国环境科学出版社,2011.
[2] Faulstich A,Stinke J K,Wittwer F.Medium voltage converter for permanent magnet wind power generators up to 5MW[C].European Conference on Power Electronics and Applications,2005.
[3] Nabae A,Takahahii I,Akagi H.A new neutral-point clamped PWM inverter[J].IEEE Transactions on Industry Application,1981,17(5): 518-523.
[4] Carrara G,Gardella S,Marchesoni M,et al.A new multilevel PWM method: A theoretical analysis[J].IEEE Transactions Power Electron,1992,7(3):497–505.
[5] McGrath B P,Holmes D G,Lipo T A.Optimized space vector switching sequences for multilevel inverters[J].IEEE Transactions on Power Electronics,2003,18(6): 1293-1301.
[6] Kanchan R S,Baiju M R,Mohapatra K K,et al.Space vector PWM signal generation for multilevel inverters using only the sampled amplitudes of reference phase voltages[J].IEE Proceedings Electric Power Applications,2005,152(2): 297-309.
[7] Ogasawara S,Akagi H.Analysis of variation of neutral point potential in neutral-point-clamped voltage source PWM inverters[C].IEEE Industry Applications Society Annual Meeting,1993: 965-970.
[8] 宋强,刘文华,等.基于零序电压注入的三电平NPC逆变器中点电位平衡控制方法[J].中国电机工程学报,2004,24(5): 57-62.Song Qiang,Liu Wenhua,et al.A neutral-point potential balancing algorithm for three-level NPC inverters by using analytically injected zero-sequence voltage[J].Proceedings of the CSEE,2004,24(5):57-62.
[9] 孟永庆,沈传文,刘正,等.基于零序电压注入的三电平中点箝位整流器中点电位控制方法的研究[J].中国电机工程学报,2007,27(10): 92-97.Meng Yongqing,Shen Chuanwen,Liu Zheng,et al.Study on neutral-point potential control method for three-level NPC rectifiers by injecting zero-sequence voltage[J].Proceedings of the CSEE,2007,27(10):92-97.
[10] Celanovic N,Boroyevich D.A fast space vector modulation algorithm for multilevel three-phase converters[J].IEEE Transactions on Industry Application.2001,37(2): 637-641.
[11] Celanovic N,Borojevic D.A comprehensive study of neutral point voltage balancing problem in three-level neutral-point-clamped voltage source PWM inverters[J].IEEE Transactions Power Electronics,2000,15(2):242-249.
[12] Yamanaka K,Hava A M,Kirino H,et al.A novel neutral point potential stabilization technique using the information of output current polarities and voltage vector[J].IEEE Transactions on Industry Applications,2002,38(6): 1572-2080.
[13] Busquets-Monge S,Bordonau J,Boroyevich D,et al.The nearest three virtual space vector PWM: a modulation for the comprehensive neutral-point balancing in the three-level NPC inverter[J].IEEE Power Electronics Letters,2004,2(1): 11-15.
