同步卫星导航试验系统广播星历设计

刘星东，雷辉，杨旭海



同步卫星导航试验系统广播星历设计

刘星东1,2,3，雷辉1,2，杨旭海1,2

（1. 中国科学院国家授时中心，西安 710600；2. 中国科学院精密导航定位与定时技术重点实验室，西安 710600；3. 中国科学院大学，北京100049）

同步卫星导航试验系统的混合星座主要由GEO和IGSO组成。针对该系统内存在的不同类型卫星轨道及GEO的小倾角、小偏心率问题，设计了一种利用切比雪夫多项式拟合卫星轨道的广播星历方案。对2013年3月的实测轨道数据进行了计算分析，并确定拟合阶数为6阶，拟合弧段长度为30min，重叠弧段为15min。计算表明该方案的拟合精度优于1cm。

广播星历；混合星座；切比雪夫多项式；拟合精度

0 引言

实时获取导航卫星位置和速度的数据是用户进行导航定位的前提条件[1]。导航卫星的位置和速度由其星历参数来表征，具体形式可以是卫星位置和速度的时间列表，或者是一组与时间相关的轨道参数。卫星通过发布星历参数，支撑用户的实时定位、精确导航等服务。因此，广播星历的表达形式直接影响导航卫星系统电文结构设计、用户算法以及系统的性能[2]。

与世界上现有的其他主要卫星导航系统相比较，同步卫星导航试验系统采用相同的时间差测量，测量各卫星导航信号到达接收天线的时间之差。不相同的是，同步卫星导航试验系统将导航频率基准和时间基准的原子钟直接安置在地面导航中心站上，利用卫星转发器转发上行导航信号后广播下行的方式实现导航定位。基于转发模式的导航卫星上不携带原子钟，导航电文在地面生成经卫星转播[3-6]，易于改变且可以频繁注入。同步卫星导航试验系统的导航星座主要由地球静止轨道卫星（GEO）和倾斜地球同步轨道卫星（IGSO）构成，并且存在小倾角、小偏心率的轨道。因此，我们需要根据同步卫星导航试验系统的特点，设计一种实用的广播星历形式。

本文在分析同步卫星导航试验系统自身特点的基础上，采用切比雪夫多项式拟合其广播星历，并详细研究了拟合参数的设置问题。

1 设计思想

GPS和GLONASS是当今世界上在轨运行的两大卫星导航系统，这两系统的广播星历参数的设计和算法各具特点。如果在具有混合星座的同步卫星导航试验系统中直接套用GPS和GLONASS的广播星历参数的设计和算法会存在一些问题。

GPS用开普勒轨道根数和相应的一些摄动系数来发布星历[7]。这组参数不适合偏心率和轨道倾角为0的卫星轨道。因为对小倾角、小偏心率的轨道而言，部分开普勒轨道根数的物理意义已经不明确，无法计算其值。另外，GPS导航定位中，观测数据量大，卫星位置计算频繁，直接按公式计算会占用大量的内存空间和计算时间。

GLONASS的广播星历直接提供参考时刻的卫星位置、速度和日月摄动加速度[8]。利用这种形式的广播星历计算卫星轨道时，由于考虑的摄动力只包括地球非球形摄动J2项、日月摄动[9]，计算结果误差较大，尤其是计算GEO卫星和IGSO卫星的轨道时。另外，计算过程较复杂，计算时需要做积分运算（四阶龙格库塔积分器），积分区间的长短和积分步长都将影响运算时间和截断误差。

通过上述分析，考虑到同步卫星导航试验系统中存在的小倾角、小偏心率的轨道，我们可以选择卫星的直角坐标数据进行拟合，这样不会涉及轨道倾角及偏心率等物理概念；同时为了降低用户算法的复杂度，可以将卫星星历表示为时间多项式，即将一定时间段内的卫星轨道拟合于选定的多项式，在内存中仅保存拟合得到的多项式系数，以备以后计算卫星位置和速度时调用。

在各种多项式中，考虑到切比雪夫多项式的逼近效果最佳，即使在时间段的两端近似性也很好[10]，相应的插值多项式能最大限度地降低龙格现象[11]，更好地保证拟合精度。因此，我们选用切比雪夫多项式拟合。

1.1 切比雪夫多项式拟合

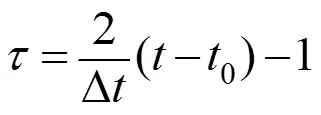
则卫星位置的切比雪夫多项式为[12]

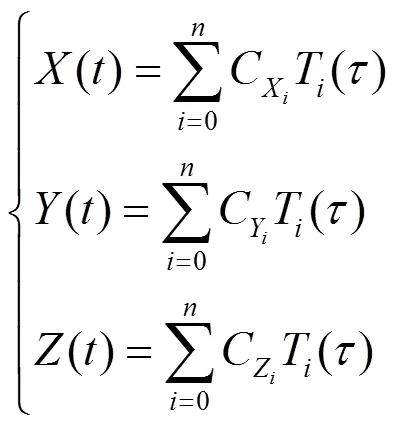
则式（4）可写成向量表达式：

利用最小二乘法，解得

1.2 设计方案

综合考虑同步卫星导航试验系统自身的特点和广播星历的时效性，拟定其广播星历方案采用切比雪夫多项式拟合，拟合弧段30min，每15min更新一次（即重叠弧段为15min），每1min注入1次，广播星历更新概况示于图1。

图1 广播星历更新示意图

接收端用户解算方法如下：

2 计算分析

由切比雪夫多项式拟合的广播星历与卫星实际轨道存在一定偏差，当拟合阶数、拟合弧段长度、拟合系数有效数字位数不同时，其偏差大小也不相同。下面将对这些因素的影响进行具体分析，寻求一组最佳的轨道拟合的参数设置。限于篇幅，本文主要利用2013年3月10日的精密轨道数据进行计算分析，GEO卫星和IGSO卫星各选1颗，其中IGSO卫星轨道倾角为54.5°。

具体计算方法：任意选取某弧段卫星轨道进行拟合，弧段内每1min选取1个已知点，每30s取一个检核点，对其拟合精度进行评定。在每个检核点处，分别用拟合的广播星历与原始精密星历比较，得到两者的差值，统计拟合精度。

2.1 拟合阶数、拟合弧段长度

表1 IGSO卫星不同拟合弧段长度和阶数的拟合精度 mm

表2 GEO卫星不同拟合弧段长度和阶数的拟合精度 mm

按照相同的方法对不同卫星不同弧段进行类似计算，结果基本相同。综合表1和表2可知：

1）一定范围内，多项式阶数取得越高，拟合精度越高。

2）当拟合精度要求一定时，拟合阶数随着拟合弧段长度的增加也要适当地增大。

2.2 拟合系数

为便于计算和节约内存，研究多项式系数的有效数字位数对拟合精度的影响是十分必要的。

表3 拟合弧段6min的拟合精度RMS的比较 mm

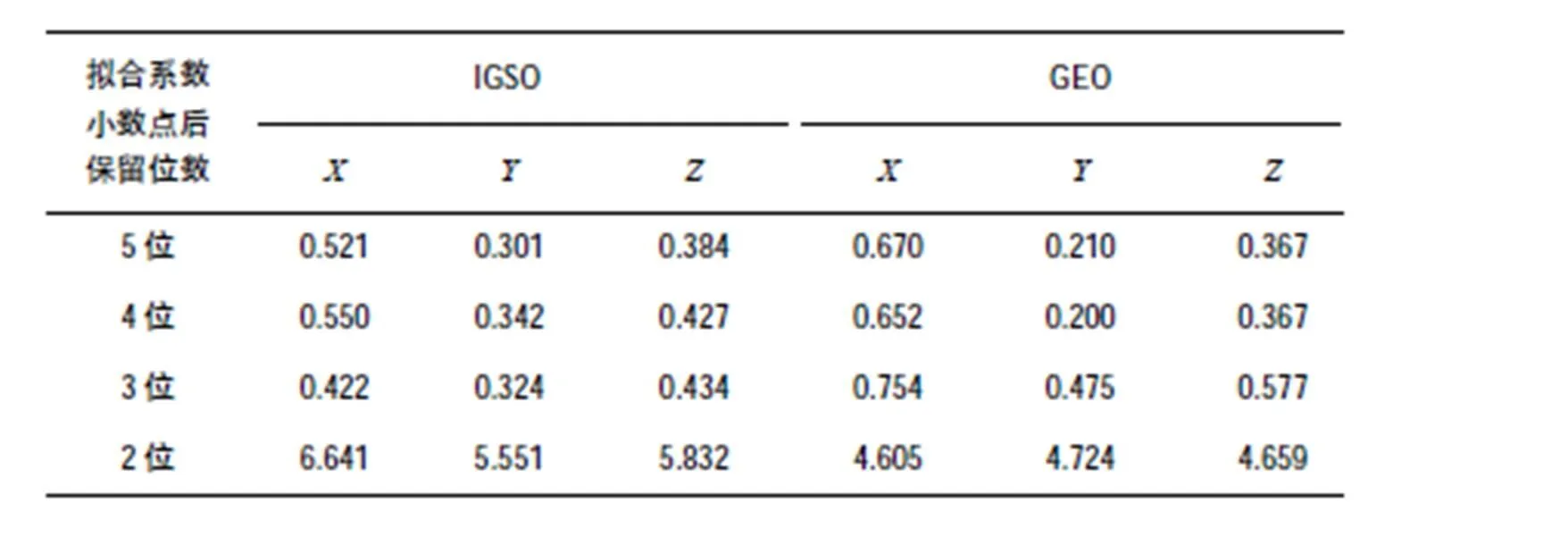
表4 拟合弧段30min的拟合精度RMS的比较 mm

按照相同方法对不同卫星不同弧段进行类似计算，结果基本相同。从表3和表4可以看出，拟合系数保留位数越多，拟合精度越高；小数点后保留位数超过3位时，拟合精度改善不明显。因此，在满足拟合精度要求的前提下，为了减小计算负荷和节约内存，拟合系数小数点后保存3位即可。

3 结论

本文主要研究同步卫星导航试验系统广播星历的切比雪夫多项式拟合，计算分析拟合阶数、拟合弧段长度等拟合参数的设置问题。通过上述计算分析可知，本文方法针对地固系下的直角坐标进行拟合，避免了小倾角、小偏心率的困扰，不会引起计算中系数矩阵奇异问题，而且用户算法简单。因此，在同步卫星导航试验系统中，拟定广播星历采用切比雪夫多项式拟合，拟合阶数6阶，拟合弧段30 min，重叠弧段15 min。经计算，该方案的拟合精度优于1 cm。

[1] 崔先强, 焦文海, 秦显平.GPS广播星历参数拟合算法的探讨[J]. 测绘科学, 2006, 31(1): 25-26, 48.

[2] 阮仁桂, 贾小林, 吴显兵, 等. 关于坐标旋转法进行地球静止轨道导航卫星广播星历拟合的探讨[J]. 测绘学报, 2011, 40(S): 145-150.

[3] 韩延本, 马利华, 乔琪源, 等. 中国区域卫星定位系统星座布局的选择[J]. 中国科学G辑: 物理学 力学 天文学, 2008, 38(12): 1671-1686.

[4] 李志刚, 杨旭海, 施浒立, 等. 转发器式卫星轨道测定新方法[J]. 中国科学G辑: 物理学 力学 天文学, 2008, 38(12): 1711-1722.

[5] 李志刚, 杨旭海, 李伟超, 等. 转发器式卫星测轨方法[J]. 时间频率学报, 2006, 29(2): 81-89.

[6] 雷辉, 李志刚, 杨旭海, 等. 基于转发式的北斗卫星导航系统地球静止轨道卫星精密定轨试验[J]. 测绘学报, 2011, 40(S): 31-33.

[7] Global Positioning Systems Directorate. IS-GPS-200G[S]. 2012.

[8] Russian Institute of Space Device Engineering. ICD L1 L2 GLONASS Edition 5.1[S]. 2008.

[9] 贾小林, 焦文海, 吴显兵. GLONASS广播星历用户算法精度分析[J]. 测绘学院学报, 2005, 22(3): 160-162.

[10] 魏子卿, 葛茂荣. GPS相对定位数学模型[M]. 北京: 测绘出版社, 1998.

[11] ZHANG Jin-hai, WANG Wei-min, WANG Shu-qin, et al. Optimized Chebyshev Fourier migration: a wide-angle dual-domain method for media with strong velocity contrasts[J]. Geophysics, 2010, 75(2): S23-S34.

[12] 余鹏, 孙学金, 赵世军. GPS定位中卫星坐标计算的切比雪夫多项式拟合法[J]. 气象科技, 2004, 32(3): 198-200.

Design of broadcast ephemeris for experimental navigation system of synchronous satellite

LIU Xing-dong1,2,3, LEI Hui1,2, YANG Xu-hai1,2

(1. National Time Service Center, Chinese Academy of Sciences, Xi′an 710600, China;2. Key Laboratory of Precision Navigation and Timing Technology, National Time Service Center,Chinese Academy of Sciences, Xi′an 710600, China;3. University of Chinese Academy of Sciences, Beijing 100049, China)

The experimental navigation system of synchronous satellite consists of IGSO satellites and GEO satellites. Due to its hybrid-constellation and GEO′s near-zero-inclination and little eccentricity, the Chebyshev polynomial is adopted to fit the orbits of navigation satellites, thereby a broadcast ephemeris for the experimented navigation system of synchronous satellite is designed. The orbit data measured during March 2013 are calculated and analyzed, and it is determined for the fitting that the polynomial order is set as 6, the fitted segmental arc corresponds to 30minutes and the overlapping arc corresponds to 15minutes. The calculations show that the fitting accuracy for this design is less than 1cm.

broadcast ephemeris; hybrid-constellation; Chebyshev polynomial; fitting precision

TN967.1

A

1674-0637(2014)04-0228-06

10.13875/j.issn.1674-0637.2014-04-0228-06

2014-02-25

国家自然科学基金重点资助项目（11033004）

刘星东，男，硕士，主要从事卫星导航方面的研究。