函数依赖导致的XML路径冗余的判定和消除 *

曹路舟

(池州职业技术学院 信息技术系，安徽 池州 247000)

由于XML(Xtensible Markup Language)在Internet上的应用非常广泛，因此XML在具体使用过程中为了得到高质量的数据，对其模式的设计就显得特别重要，而其中DTD(Document Type Definition)模式的设计一直倍受广大XML研究者关注。DTD模式的研究主要包括以下几个方面的内容：怎样判定一个DTD模式设计是否良好；如果是一个设计不好的DTD，我们要通过什么样方法将其转化成一个满足要求的好的DTD模式等。如何来判定一个DTD设计是否良好呢？其主要依据是检查该DTD有没有存在着数据冗余信息，如果存在着数据冗余信息，它就和关系数据库一样，会引起XML文档的插入、删除、更新等操作异常，这势必影响到XML在不同应用程序之间的数据表示和交换上的使用。

本文利用XML层次结构特点，从路径的角度出发，提出了由XML函数依赖引起的XML文档树有路径冗余的几种可能存在的情形，并相应的给出了消除冗余的方法及其相关的正确性证明，最后通过具体的实例验证了定理的正确性和有效性。

一、相关定义及符号声明

定义1(XML路径)给定DTD D(E,A,P,R,r)和满足D的XML文档树T( V,lab,ele,att,val,root),文档树T中的路径可以定义如下：路径q=v1.…. vn,其中,v1=root, vk∈ele(vk-1), (k=2,…,n-1)。若lab(vn)∈E，vn∈

ele(vn-1)， P(lab(vn))≠S，则称该路径q为元素节点型路径；若lab(vn)∈A，vn∈att(vn-1)或lab(vn)∈E，vn∈ele(vn-1)，P(lab(vk))=S，则称该路径q为值类型路径。

XML路径说明：

(1)令last(q)=vn,表示路径q中的最后一个节点，q-last(q)表示路径q在除去最后一个节点路径后的路径，本文仅考虑最后一个元素不为空的情况；

(2)Paths(T) 表示文档树T中所有路径的集合,即Paths(T)={q|q是T中的路径}；其中EPaths(T) 、APaths(T) 、VPaths(T)分别表示元素节点类型路径的集合、属性值类型路径的集合和文本值类型路径的集合，即EPaths(T)={q|q∈Paths(T)且lab(last(q))∈E}、APaths(T)={q|q∈Paths(T)且lab(last(q))∈A}和VPaths(T)={q|q∈Paths(T)且last(q)∈E，P(lab(last(q)))=S}。

定义2(路径包含) 两条路径r1,r2，(r1,r2∈Paths(D))，如果r1只是r2的一部分，则可表示为r1⊂Pathsr2；如果r1可能是r2的一部分也可能是完全一样，则可表示为r1⊂Pathsr2。

定义3(树元组) 给定DTD D=(E,A ,P,R,r)和满足D的XML文档树T=(V , lab , ele , att , val , root)，树元组t被定义成Paths(D)到V∪S∪{⊥}的映射，则t会满足以下几种可能情况：⑴若q∈EPaths(D)，则t[q]∈V∪{⊥}，且t[q] ≠⊥；否则t[q]∈S∪{⊥}；⑵若t[q1]=t[q2]且t[q1]∈V，则q1=q2；⑶若t[q1]=⊥且q1是q2的前缀，则t[q2]=⊥；⑷{q∈Paths(D)|t[q] ≠⊥}不是无限的，而是有限的。

上述定义中的S表示为字符串值,⊥表示为空值，树元组t[q]也可以表示为t.q，同时本文用T[T]={t|t∈T}来表示所有树元组的集合。

定义4 (节点值相等)对于一个给定DTD D=(E,A,P,R,r)和满足了这个给定D的XML 文档树T=(V , lab,ele,att,val,root)，r1和r2是V中的节点，r1与r2是值相等记为r1=vr2，充分必要条件是：(1)lab(r1)=lab(r2)；(2)若r1和r2是A节点或者S节点，则val(r1)=val(r2)；(3)若r1和r2是E节点，则1)∀m1∈att(r1)， m2∈att(r2)，满足m1=vm2，反之同样成立；2)若ele(r1)=v1,…,vk，ele(r2)=v1’,…,vk’，则所有的i∈[1,k]，都有vi=vvi’。

定义5 (函数依赖FD) 给定DTD D=(E , A , P , R , r)和D上的函数依赖FDφ：

(Sh,[Sx1,…,Sxn]→Sy)，对于满足了D的XML文档树T，则称T满足函数依赖φ充分必要条件是对T(T╞D)中任意两个t1和t2(树元组)，在Sh约束范围内，如果有t1[Sxj]=vt2[Sxj]，(j=1,2,…,n)，则一定有t1[Sy]= vt2[Sy]。

函数依赖FD的说明：

(1)Sh、[Sx1,…,Sxn]和Sy分别表示函数依赖φ的头部路径、左部路径和右部路径，其中Sh∈Paths(D)，Sxj∈Paths(D)(j=1,2,…n)，Sh⊆PathsSxj,而Sy∈Paths(D)或Sy=ε，Sh⊆PathsSy；

(2)若Sh=φ，叫做绝对函数依赖，即表示φ在整个D上都是成立的，否则叫做相对函数依赖；

(3)若Sy=(Sy为空时)，FD本身是无任何意义的，但由于XML是层次结构，如果没有此说明，就会丢失层次之间的约束关系。

如图1中存在函数依赖FDφ:(college.course,[college.course.student.sno] →college.course.student.grade)等。

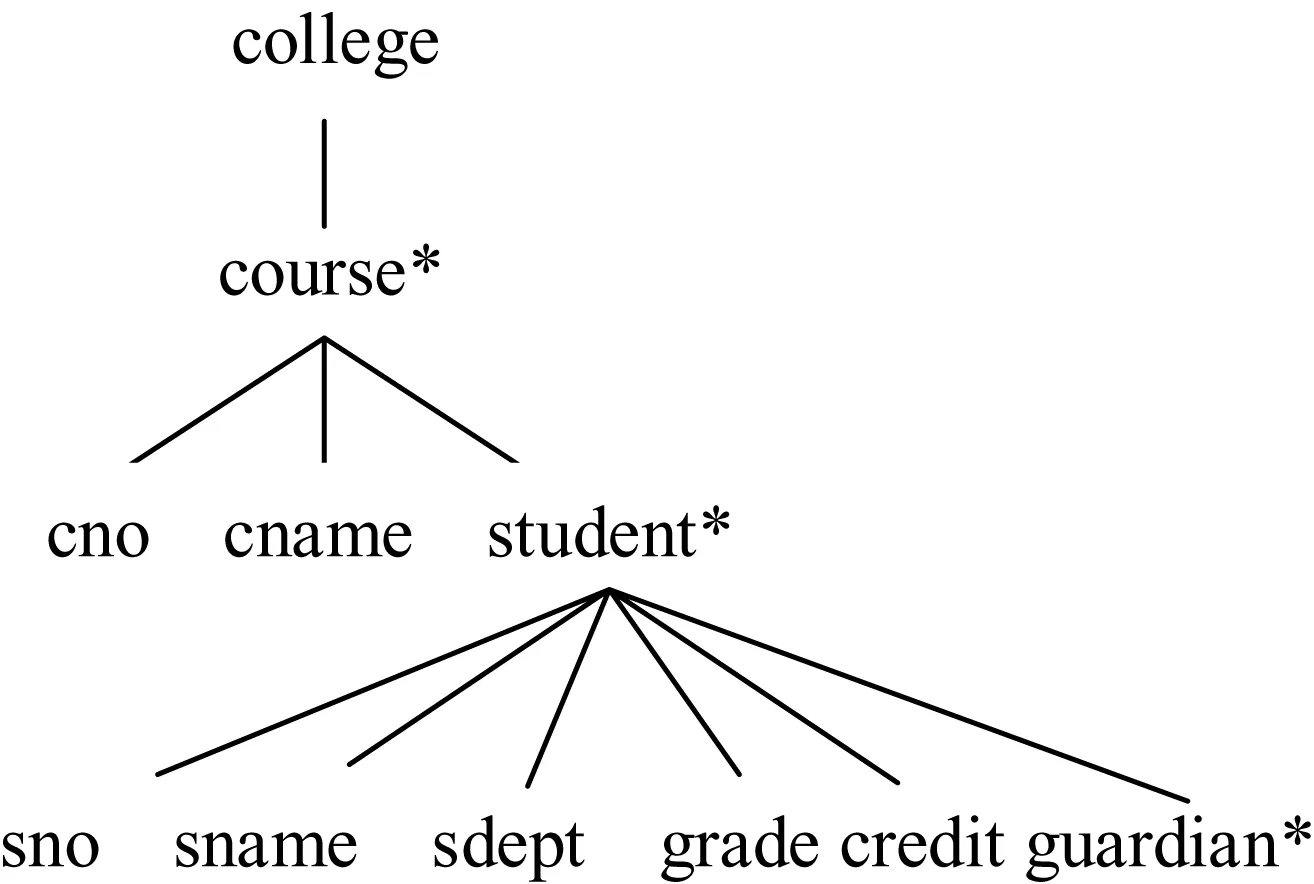
图1 一个有路径冗余的DTD D结构

定义6(键)给定T╞D，∀t1,t2∈T[T]，路径S⊂pathsSy⊂pathsSk(k=1,2,…,n)，其中last(Sy)*∈P(last(Sy-last(Sy)))，last(Sk)∈E∪A。若t1[S]=t2[S]且t1[Sk]=vt2[Sk]成立时t1[Sy]=t2[Sy]也成立，则称在S的约束范围内，[S1,S2,…,Sn]唯一标识路径Sy，定义S[S1,S2,…,Sn]为Sy的键，如果没有{S1’,S2’,…,Sm’}⊂{S1,S2,…,Sn}，S[S1’,S2’,…,Sm’]也是Sy的一个键，则定义S[S1,S2,…,Sn]为Sy的主键，键子树是指以last(Sy)为根的子树。

在图1中，在college.course的约束范围下，由键的定义得知college.course[college.course.student.sno]既是college.course.student的一个键，同时也是它的一个主键。

定义7(外键) 给定D上S[S1,S2,…,Sn]为Sy的一个键，在路径H(S⊂pathsH)范围内，有一组路径H1,H2,…,Hm。若S为根的子树中，T[H[H1,H2,…,Hm]]⊆T[S[S1,S2,…,Sn]]，则[H1,H2,…,Hm]是H相对于S[S1,S2,…,Sn]的一个外键。

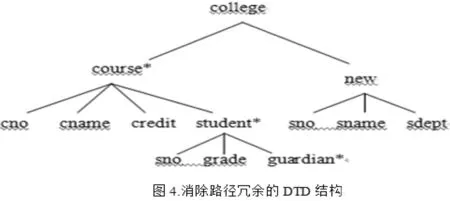
如图4中，college.course[college.course.student.sno]是college.course.student的键，又是college.course相对于college. new.sno的外键。

二、XML路径冗余判定和消除算法

1.路径冗余

数据冗余可以直观的理解为同一对象数据的重复存储,若某对象数据在同一路径上被重复存储，则称为路径冗余。如图1的结构中，路径college.course.student.credit就是路径冗余。

2. 受键子树以外的其他路径约束

如图2(a)结构所示：这是一种在键子树内的路径被不是该键子树内的其他路径约束的一种情况。

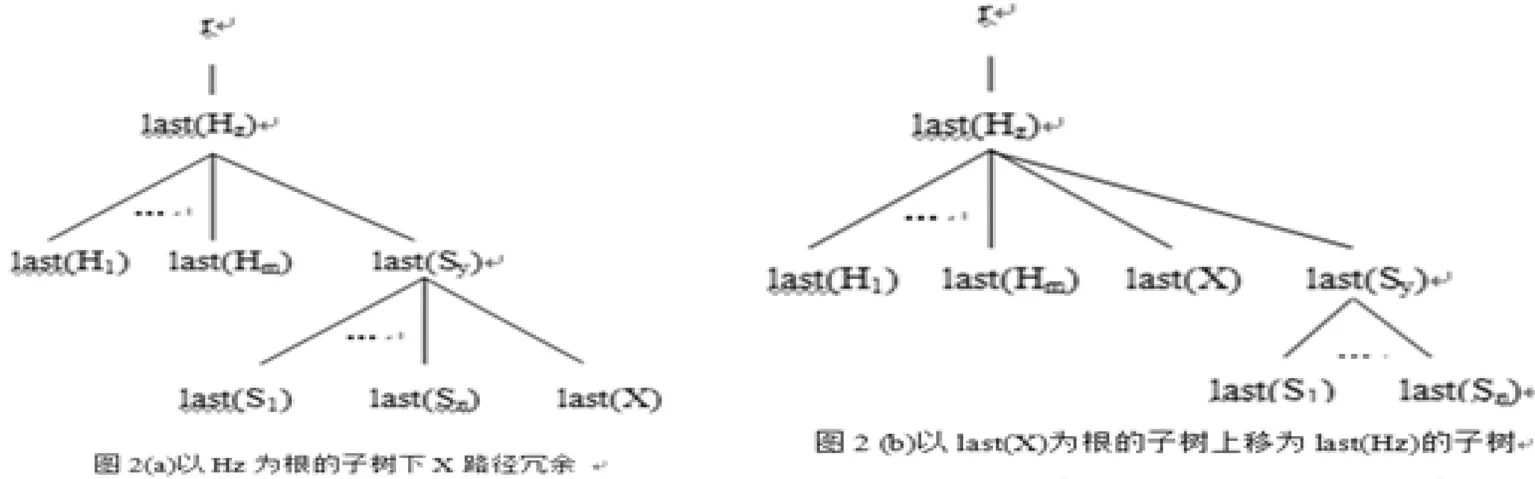
【定理1】D上S[S1,S2,…,Sn]为Sy的键，且有FD φ：Hz[H1,H2,…,Hm→X]，其中Hz⊂pathsSy⊂pathsX，last(X)∈P(last(Sy))，last(Hj)∉P(last(Sy))，last(Hj)∈P(last(Hz))(j=1…m)，则T(T╞D)中以Hz为根的子树下X路径冗余。

证明：由于S[S1,S2,…,Sn]为Sy的键，Hz⊂pathsSy，故文档树T(T╞D)在以Hz为根的所有子树中，很多次的出现了Sy路径；又由于last(X)∈P(last(Sy))，故出现的每一条Sy路径都存在着与之相对应的X路径；同时last(Hj)∈P(last(Hz))，故而在文档树T(T╞D)以Hz为根的所有子树中，Hi(i=1…m)路径会出现一次，而且是仅出现一次。

所以存在j个不相同的树元组t1,t2…，tj，在Hz，[H1,H2,…,Hm]上结点一样,而在Sy上结点却互异。又φ：Hz[H1,H2,…,Hm→X]，因此这些树元组在不同的Sy子树的X路径上结点值必定一样。因而在Hz为根的所有子树中，就存在着j条一样的路径X，即T(T╞D)中以Hz为根的子树下X路径冗余。

证毕。

如图1中，依据定理1，路径college.course.student.credit在college.course.student键子树中被该键子树以外的路径college.courses.cno相约束，从而出现了路径冗余。

如何消除定理1中出现的路径冗余呢？解决的方法就是将冗余的X路径移出键子树，以last(X)为根的子树往上移成last(Hz)的子树即可。如图2(b)所示。消除定理1中X路径冗余的具体算法描述如下：

【算法1】

步骤1：寻找满足定理1中所描述情况的最大的X子树。

若存在着路径X'，函数依赖φ'：Hz[H1,H2,…,Hm →X']，Sy ⊂pathsX'⊂pathsX，则用X'替代X，用φ'替代φ，重复步骤1，直到没有路径X'结束。

步骤2：D=(E,A,P,R,r)变换为D'=(E,A,P',R',r)，根是last(X) 结点的子树结构整体往上移动，变成last(Hz)结点的子树。

算法描述结束。

证明：在D上以Hz为根的子树中，X路径在last(Sy)子树中重复出现k次。在D'上，last(X)为根的子树与last(Sy)子树语义无关，以Hz为根的子树中X路径只出现一次。证毕。

3. 在键约束范围以外受键约束

如图3(a)结构所示:这是一种键对键子树内的路径的约束超过了键本身的约束范围。

【定理2】D上S[S1,S2,…,Sn]为Sy的键，且存在FD φ：G[S1,S2,…,Sn→X]，G⊂pathsS⊂pathsSy⊂pathsX，

last(X)∈P(last(Sy))，则在T(T╞D)中以G为根的子树下X路径冗余。

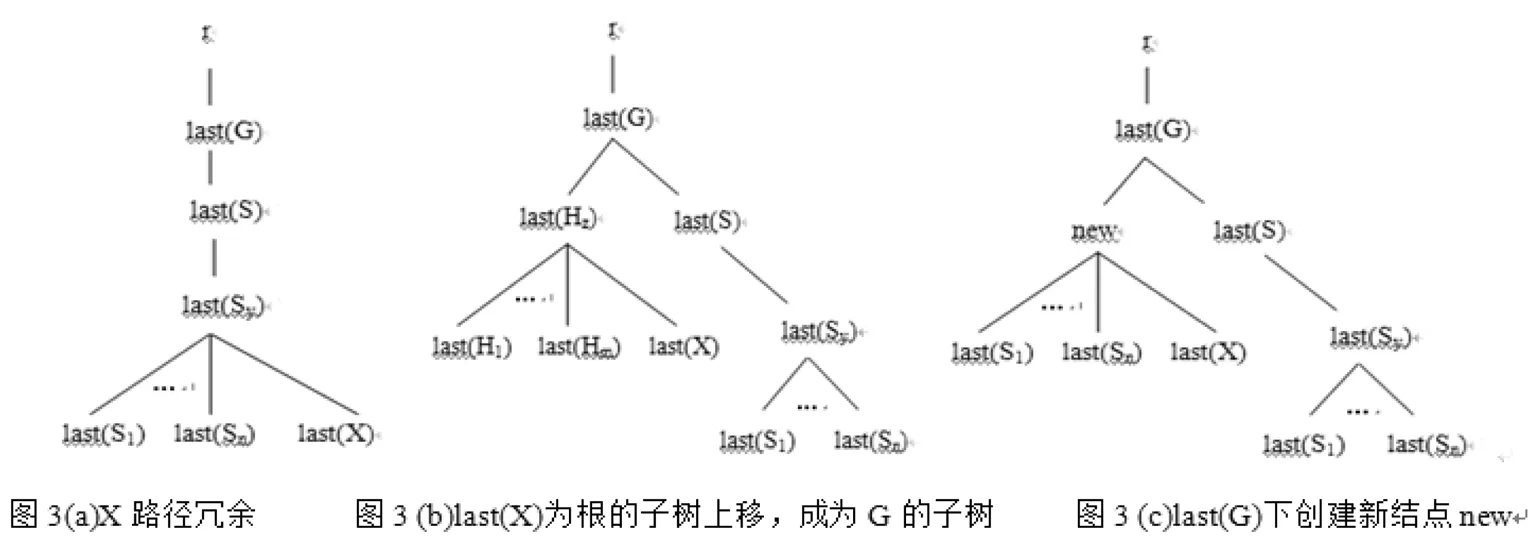
定理2适合用反正法证明，具体证明过程如下：

证明：假设在文档树T(T╞D)中以G为根的所有子树下[S1,S2,…,Sn]路径无重复出现，即在G的约束范围内，Sy可以被[S1,S2,…,Sn]所唯一标识，根据前面键的相关定义可以得出S是[S1,S2,…,Sn]唯一标识Sy最大的约束范围，即S⊆pathsG。这与条件中G⊂pathsS不相符，因而假设不能够成立，在T(T╞D)中以G为根的子树下[S1,S2,…,Sn]的路径存在着冗余。又由于函数依赖FD φ：G[S1,S2,…,Sn→X]，所以[S1,S2,…,Sn]路径冗余必定也会导致T(T╞D)中以G为根的子树下有X路径冗余的存在。

证毕。

如图1中，路径college.course.student.sdept就是定理2中描述的这种路径冗余。

消除定理2中的X路径冗余的方法跟消除定理1的方法不同，它是将原T(T╞D)中的键变成其他键的外键。如果[S1,S2,…,Sn]是S相对于G[H1,H2,…,Hm]的一个外键，则将last(X)为根的所有子树往上移动到G结点下，成为其子树，如图3(b)所示。否则，在last(G)下创建一个新结点new，根是last(X)结点的子树结构往上移动到new结点下，成为其子树，而根是last(Si)的子树结构也整体复制到新结点new下，从而使[S1,S2,…,Sn]是S相对于G[G.new.last(S1),G.new.last(S2),…,G.new.last(Sn)]的一个外键，如图3(c)所示。消除定理2中X路径冗余的具体算法描述如下：

【算法2】

步骤1：寻找满足定理2条件中的最大范围的G。

如果存在G',存在函数依赖FD φ'：G'[S1,S2,…,Sn →X], G'⊂pathsG，则用G'替代G，用φ'替代φ，重复步骤1，直到没有路径G'结束。

步骤2：如果存在着路径组{H,H1,H2,…,Hm}，G[H1,H2,…,Hm]是H的键，[S1,S2,…,Sn]是S相对于G[H1,H2,…,Hm]的一个外键，则D=(E,A,P,R,r)变换成D'=(E',A,P',R',r)，E'=E，∀τ∈E，R'(τ)=R(τ)，P'(τ)=P(τ)，新结点new为last(H)，则跳过步骤3直接进入步骤4；

步骤3：D=(E,A,P,R,r)变换成D'=(E',A,P',R',r)，同时在last(G)下创建一个新结点new，而以last(Si)(i=1，

…，n)为根的所有子树的结构都复制到new结点下成为new结点的子树。

步骤4：寻找满足上述情况的最大X子树。

如果存在路径X'，FD φ'：G[S1,S2,…,Sn→X']，Sy⊂pathsX'⊂pathsX，则用X'替代X，用φ'替代φ，重复步骤4，直到没有路径X'结束。

步骤5：根是last(X)结点的子树结构往上移动，成为新结点new的子树，更改D'=(E',A,P',R',r)。

算法描述结束。

证明：由定理2为例证明。若[S1,S2,…,Sn]是S相对于G[H1,H2,…,Hm]的一个外键，原D上φ在D'上改为φ'：G[H1,H2,…,Hm→G.new.last(X)]，G.new.last(X)没有路径冗余

若[S1,S2,…,Sn]不是S相对于G[H1,H2,…,Hm]的一个外键，经过步3在D'上，[S1,S2,…,Sn]是S相对于G[G.new.last(S1),G.new.last(S2),…,G.new.last(Sn)]的一个外键。同上，以G为根的子树下，G.new.last(X)路径冗余就没有了。证毕。

三、消除函数依赖导致的路径冗余实例

依据定理1和算法1，credit节点从student节点下移走，插入到course节点下；

依据定理2和算法2，建立new结点，sno和sname,sdept为其子结点。

函数依赖导致的XML路径冗余就消除了，如图4所示。

四、结束语

从文中实例可以得出：产生路径冗余的原因是由于一棵子树的根与这棵子树中其他的数据都存在着一定的关联，使语义上本来毫无联系的数据在树中也形成了层次约束。消除路径冗余的方法就是理顺树中这种语义约束关系。文章在已有的研究基础之上，给出了由于函数依赖而产生的路径冗余的判定及其消解过程，然而多值依赖同样也会导致路径冗余，而且也比函数依赖导致的路径冗余要复杂的多，怎样解决多值依赖导致的路径冗余，这是以后进一步要研究的内容，同时路径冗余的研究对XML范式研究和保障XML正确应用有着积极的意义。