一种改进的最大m子段和算法设计*

2014-06-21廖作斌

湖北科技学院学报 2014年3期

廖作斌

(泉州师范学院数学与计算机科学学院，福建泉州 362000)

最大m子段和问题是ACM/ICPC程序设计竞赛典型而且常见的算法题型，其描述如下：给定由n个整数(可能为负)组成的序列a1，a2，a3，……，an，以及一个正整数m，要求确定序列的m个不相交子段，使这m个子段的总和最大！亦即，给定n个整数求这n个数划分成互不相交的m段的最大m子段和。

最大m子段和的经典动态规划优化方法是：设b(i, j)表示前i个数划分成j段，且包括第i个数的最大m子段和，那么有状态转移方程：

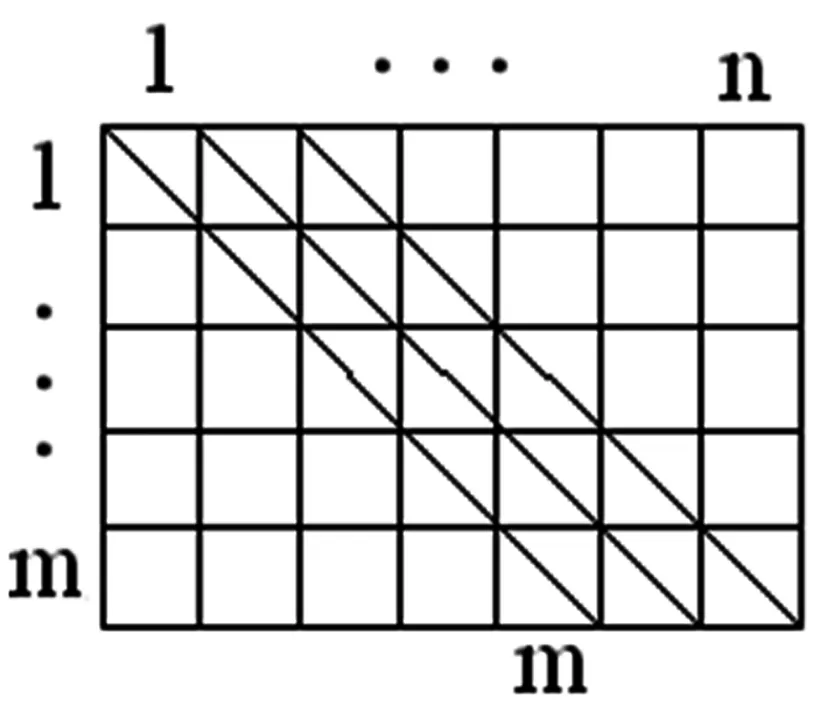
b[i][j]=max{b[i-1][t],b[i][j-1]}+a[j] (1<=i<=m, i<=j<=n, i-1<=t

初始条件：b[t][0]=0(0<=t<=m)，b[0][t]=0(1<=t<=n)

max{b(m,j)}(m<=j<=n)即为n个整数序列的最大m子段和问题最终解。

算法基本思想为按上述状态转移方程构造一个m+1行(假设第0～m行)，n+1列(设第0～n列)的二维数组b，则第m行的最大元素为问题最终解。但实际设计算法时不必构造二维数组，因为只有第m行的最大元素为问题最终解，因此不必保存中间结果，经优化后得到如下经典算法：

int MaxSum(int m,int n,int *a) {

int i,max,j,sum;

if(n

int *b=new int[n+1]; int *c=new int[n+1];

b[0]=0;

for(i=1;i<=m;i++) {

b[i]=b[i-1]+a[i]; c[i-1]=b[i]; max=b[i];

for(j=i+1;j<=i+n-m;j++) {

b[j]=b[j-1]>c[j-1]?b[j-1]+a[j]:c[j-1]+a[j];

c[j-1]=max;

if(max

}

c[i+n-m]=max;

}

sum=0;

for(j=m;j<=n;j++)

if(sum

return sum;

}

算法1 动态规划常规算法

一、常规算法分析

下面对常规算法进行分析，计算过程如图1所示：

图1 常规算法计算过程

算法中需要两个长度为n+1的辅助数组b和c，数组b用于保存第i行的数值，需要计算i+n-m个数值(因为最终解是最后一行的最大值，按状态转移方程，需要已知第m-1行第1～n-1列的数值，以此类推，如图1斜线所示)；数组元素c[j]表示当前行从第一个元素到第j个元素的最大值，同样也需要计算i+n-m个数值。

该算法虽然已经过优化，不必计算整个二维数组，只需保存一行数值以及该行从第一个数值到任一数值的最大值，而且不需要计算每一行的全部数值(如图1)，但进一步分析发现，当计算第i行时，前面i-1个数值是无意义的，因为分成i段必须保证不少于i个数值，因此每一行需要计算的数值其实是一样的，即n-m+1个。计算过程如图2所示，图中斜线部分即每一行需要计算的数值。