利用积分确定函数方程的方法探析*

张秋生

(新乡职业技术学院，河南 新乡 453000)

通过对微积分的研究，分析如何更好地确认相关的函数方程。纵观历年的考试，我们不难知道如下的方法：

一、利用微积分极限确定相关的函数方程

在高等数学中，关于函数的极限求解是重要的解题方法，要知道，在实际问题的精确解中，仅仅通过有限次的算术运算是不足以求解的，必须通过无穷变化过程的变化趋势才能更好地求解，因此我们就有极限的概念以及相关的极限方法。通过利用微积分极限能够更为有效地确定具体的函数方程。以下是其简要分析：

数学题型解题方法 函数方程无穷小的比较或确定无穷小的阶1.比较两个无穷小,并按照相关的定义,运用洛必达法则以及等价无穷小代换;2.通过三个或三个以上的无穷小的比较,利用等价无穷小代换化简,然后对无穷小作比较,主要运用洛必达法则;3.确定其无穷小的阶,主要运用 limx→∞f(x)xn为有限数确定n,确定n时,主要运用洛必达法则以及等价无穷小代换此方法。 确定未定式的函数方程的极限1.通过因式分解或根式有理化,消去使分母去零的因式,并运用极限运算法则或连续函数的性质求解。所谓的根式有理化,是指极限式中的含有 a±b分别乘以分子或分母,使其“0”因子呈现的运算。 确定∞∞型函数极限1.运用抓大头原则;2.运用洛必达法则;3.利用变量代换化为 00。确定∞-∞型函数1.通分或根式有理化将其转化为00型;2.利用倒代换 x=1tk(常数k>0) 。 确定0-∞ 型未定式函数1.通过“0”或“ ∞”项下放(放到分母的位置上)转化为00型或 ∞∞型,然后运用洛必达法则或抓大头准则。

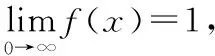
且f(X)>0，且满足求f(X)。

为1∞=eλ型极限，以下是简要的运算：

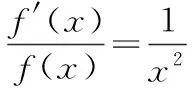
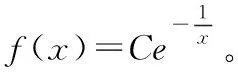
例2 设f(x)在x=0中有界限，且满足方程f(x)-1/2*f(x/2)=x2，求f(x)。

解：f(x)-1/2*f(x/2)=x2

1/2*f(x/2)-1/22f(x/22)=1/2*(x/2)2;1/22*

f(x/22)-1/23*f(x/23)=1/22*(x/22)2

......

1/2n-1*f(x/2n-1)-1/2n*f(x/2n)=1/2n+1*(x/2n-1)2

将以上的诸式相加，我们就能知道如下：

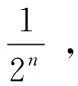
二、利用导数求解函数方程

关于函数中的导数与微分是微积分学中最基本又是最重要的两个概念。在几何上函数的导数即曲线的切线斜率，因此导数有着鲜明的几何意义。在实际数学运用中，我们不难知道，导数概念在几何上的应用就是求解曲线的切线或法线的斜率。一元函数可微性与可导性是等价的，它是函数增量与自变量增量之间的关系表达式，函数的微分更多的是体现一个函数增量的线性部分。它们两者是等价的。我们在研究函数方程的时候，需要将其与可微与微分相互结合，因为它更好地描述“以直代曲”——在曲线上运用切线点求近似曲线。微分，特别是一阶微分形式的不变性是求导的逆运算的基础，运用微分近似函数的增量求解函数方程。以下是其相关实证分析：

例3 设f(x)是以5为周期的连续函数，且在x=0的领域内有

f(1+sinx)-3f(1-sinx)=8x+α(x)

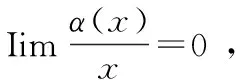
解：因题设可知，f(x)=f(x+5) ，f(6)=f(1) ，f′(x) =f′(x+5)，f′(6)=f′(1).式(1)中的两边取x→0时的极限，得

F(1)-3f(1)=0→f(1)=0，即f(6)=0

式中(1)的两边同除以x，然后取x→0时的极限.

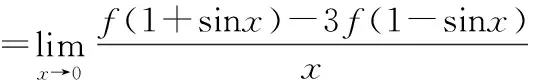
=f′(1)+3f′(1)=4f′(1)

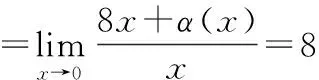
所以4f′(1)=8f′(1)=2，即f′(6)=2 ，故曲线y=f(x)在点(6，f(6))处的切线方程为：y-f(6)=f’(6)(x-6)，即y=2(x-6)。

三、利用可变上限求导求解对应的函数方程

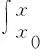
f[ψ(x)]ψ′(x) -f[ψ(x)]ψ′(x)(x∈I).通过运用其定义，我们能够推导到相关的函数，并对定积分或变限积分中的被积分含f{ψ(x)}，一般以变量代换，将f{ψ(x)} 变为f(μ) ，在切换的过程中，需要注意相应更换积分的下限。以下是实证分析：

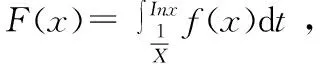
解：因为它是连续函数，即不需考虑到其极限情况，直接求导即可，如下所示：

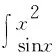
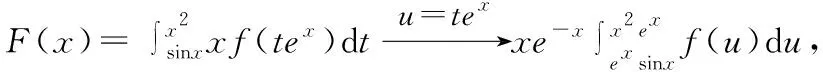
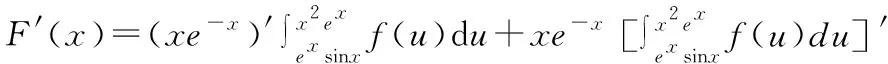
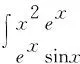
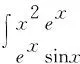
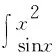
四、依据函数的连续性确定函数方程

按照函数连续性的定义，我们不难知道，如果函数f(x)在点x=a处及其附近有定义，而且函数在x=a处的极限值和f(a)相等，就说函数f(x)在x=a处连续。函数若在区间(m，n)内所有点上都连续，就说函数在区间(m，n)内连续。函数若在区间(m，n)内所有点上都连续，而且在x=m点上右极限等于f(m)，在x=n点上左极限等于f(n)，我们就能说函数在区间[m，n]内连续。在确定函数方程中，我们不难知道，通过f(x)在x=a的两侧表达式差异，我们能够确定其具体的函数方程。

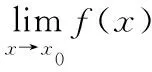
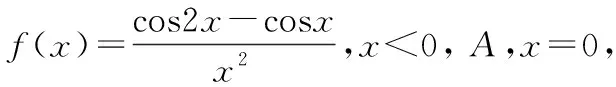
解：由题设，有f-(0)=f+(0)=f(0)=A，而

则-3/2=1+B=A，故A=-3/2，B=-5/2。因此可确定其方程大小。

故：

五、利用微积分方程的性质求解方程

函数是客观反映事物内部联系在数量方面的反映，利用函数关系我们能够更好地研究客观事物的规律，对于理解变量之间的关系有着必要性，在实践中有着更为重要的意义。但是在实际的过程中，我们并不能直接确定其函数的关系，需通过变量与函数之间的关系确定其中的关系，此就是微分方程，通过方程的运算，我们能够更好地确定函数方程。

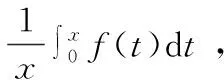
解：曲线y=f(x)在点(x，f(x))处的切线方程为：Y-f(x)=f’(x)(X-x)

令X=0，得截距Y=f(x)-xf’(x)。

函数是数学中的重要组成部分，它反映更多的是变量之间的关系，而我们知道，任何事物都是变化发展的，数学就是一个结构复杂的机器，任何一个零件都有着其独特的功能，积分的应用在几何、物理、工程技术、经济类等诸多领域有着广泛的应用，是一元函数积分学的核心。而定积分与不定积分，我们在实际学习的过程中，不难知道，它们能够给出被积函数的全体原函数，从而为积分计算提供更为简捷的工具。通过对积分方法的归纳总结，更好地实现函数方程确定的客观规律。

参考文献：

[1]同济大学应用数学系.高等数学[M].北京：高等教育出版社，2006.

[2]陈文灯.考研数学核心题型[M].北京：北京航空航天大学出版社，2010.

[3]张宏志.高等数学教与学参考[M].西安:西北工业大学出版社，2002.