低分辨机载雷达飞机目标分类识别技术研究

王福友 罗 钉 刘宏伟

①(中国航空工业集团公司雷华电子技术研究所 无锡 214063)

②(西安电子科技大学雷达信号处理国家重点实验室 西安 710071)

1 引言

作战指挥中心的重要需求之一就是情报信息获取，包括目标的属性及威胁程度的评估，这就要求机载雷达具有非合作目标识别的能力，同时该技术也是空战中关键技术之一。由于近年来飞机种类的增多，以及作战面临的新局势，飞机目标分类识别技术给机载雷达带来了新的迫切需求，若机载雷达能够有效分类识别空中的各种非合作飞机目标，这将为武器系统对目标进行威胁评估和精确打击提供重要的依据。

战机上的敌我识别(Identification Friend or Foe,IFF)系统在战斗中具有被截获和失败的风险，而且并不能进行所谓的 Postive ID，而且作为雷达希望具有独立的非合作目标识别能力[1]。

近些年来，对于地基雷达来说，基于宽带成像(HRRP和ISAR成像)认为对于飞机目标分类识别具有潜力[2－5]，而对于机载雷达少有报道。对于HRRP和ISAR往往要求雷达工作在大瞬时带宽高信噪比工作模式下，此外，HRRP对方位较敏感，以及ISAR要有大转角和运动补偿等措施才能成像，这都对雷达系统提出较高的要求。

基于极化信息的飞机分类识别国外也有报道[6]，这往往对雷达天线、极化隔离度以及极化标校要求较高。文献[7]给出了基于 EMD-CLEAN算法的低分辨雷达飞机目标分类识别研究结果，给出了较好的分类识别结果。

针对以机载雷达为平台的非合作飞机目标识别，特别是针对窄带特征的目标识别，因为窄带特征目标识别意味着耗费资源少，便于实现，国内外公开的文献少有报道。国外在基于窄带特征识别方面有基于JEM (Jet Engine Modulation)喷气发动机引擎谱调制特征的飞机目标识别[8]，这往往对调制特征非常明显的飞机比较有效，而由于JEM谱调制是基于发动机调制进行的，要充分研究发动机的调制特性，要有先验信息，就是对不同飞机安装的发动机型号，以及不同飞机安装的发动机的各级转子的桨叶数有先验信息，这对于实际情况是较难获取的[1]。JEM调制是多普勒信号标记的一个子集，即使使用同种类型的发动机使用方面也常常有变化，例如压缩机叶片的数量或发动机数目，所以可以进行独特的类型识别。由于飞机的振动、摇摆和速度等多重因素影响下，使得JEM实际图像并不太清晰[9]。

而对于机载雷达的飞机目标识别，可能由于保密等原因国内外很少有报道。文献[1]表明美国的F-22猛禽战斗机、美国的E-2C预警机、欧洲的台风战斗机雷达都具有目标分类识别功能，而具体采用何种识别技术和算法没有披露[1]。

分形(fractal)是近些年来非线性科学的一个重要分支，分形是为了表征复杂图形和复杂过程首先引入自然科学领域的，它的原意是不规则的、支离破碎的物体。Mandelbrot给出较全面的“分形”定义：其组成部分以某种方式与整体相似的形体叫分形[10]。自然界存在许多分形现象：如海岸线、山形、雪花、河川、岩石、裂谷、树枝、云团、闪电、草丛等。由于气象杂波以云团等构成因此具有分形特性，而有关研究表明海杂波和地杂波也具有分形特性[10,11]。由于海杂波、气象杂波和地杂波具有分形特性，所以分形被广泛应用到雷达目标检测领域，这是因为目标和杂波的分形维数差异性比较明显，如基于分形特征的海杂波背景下的目标检测[10]、地杂波背景下的目标检测[11]。多位学者研究表明基于分形可很好地对雷达电磁散射场进行数学建模[12－14]、重构雷达目标回波信号[15－17]、目标几何外形描述和目标分类[17]。

近年来，分形被认为在识别领域具有潜力，如分形被用来进行自然文理识别[18,19]，SAR目标分类识别[20]，乐器信号分类识别[21]。由于机载雷达飞机目标多在气象杂波和地海杂波背景下，而同一目标的分形维数比较稳定，且不同目标由于几何外形和调制特性的不同，其分形维数也不同，这就为基于分形特征的飞机目标分类识别成为可能。同时，有关研究[15,22]表明，分形特征不受噪声的影响，这对于雷达目标识别具有实际意义。

此外，由于目标的运动，导致目标的雷达回波幅度具有起伏特性，而幅度调制可以很好地表征回波序列的起伏特性，故提取回波序列的频域幅度调制特征可作为识别特征之一。

考虑识别效果的稳健性，以及现有机载雷达普遍具有窄带跟踪模式条件下，本文提出基于窄带分形和幅度调制特征的机载雷达目标分类识别算法。本文提取了喷气式战斗机、螺旋桨飞机、直升机 3类飞机的分形和幅度调制特征，实测试飞数据验证结果表明本文方法在小样本条件下具有较好的分类识别效果。

2 识别基本原理

2.1 分形特征识别原理

分形是描述物体表面的粗糙程度和不规则程度，分形的一个重要特征为计算的分维数是一种非整数的形式，称为分形维数，描述分形特征的参数叫分形维数。而常规的人造物体如飞机通常具有相对规则的几何形体，且目标的分形维数相对稳定，而不同飞机目标的外形存在差异，因此不同的目标在杂波中表现的分形特征也存在差异，这就为基于分形特征来识别目标的差异带来可能。

由于时间资源对于目标识别是至关重要的，本文拟定采用盒维数法来提取分形特征，盒维数法被认为是计算分形维数最快和实用的方法[10,22]。

设D是Rn上任意非空的有界子集，N (d)是直径最大为d，并可以覆盖 D的集的最小个数，则 D的下、上限的盒维数分别定义为：

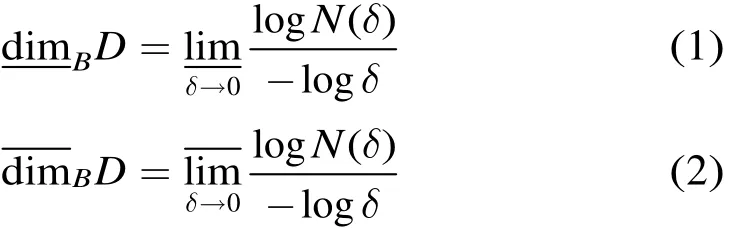
如果式(1)和式(2)两个值相等，则称D为盒维数，记为：

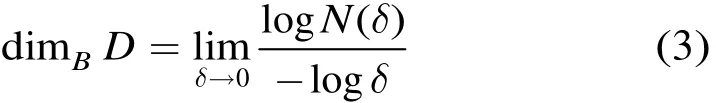
由式(3)即可计算出盒维数。

盒维数算法可以理解为，取边长为d的小盒子，把分形覆盖起来，由于分形内部有各种层次的空洞和缝隙，有些小盒子会是空的，数数有多少非空盒子，把这个数目记为 N( d)，然后缩小盒子尺寸d,N( d)自然要大，根据定义只要在双对数坐标系上画出log N( d)和log d的曲线，其直线的斜率即为盒维数。

图1给出的是基于盒维数法计算分形维数的算例，用 d= 1/10的小盒子把序列所在单位正方形分成 100个小方格，覆盖分形曲线带阴影的盒数N( e) = 58，则盒数维：

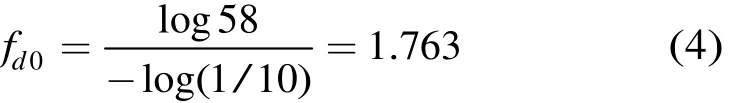
由于习惯上称分形的特征是分形维数，盒维数是分形维数计算的一种方法，因此得到分形维数(fractal dimension)

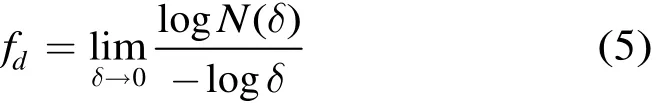
式中 Nd( D)在实际计算中一般取大于含目标的距离单元点数，设含有目标的距离单元的点数为N，令

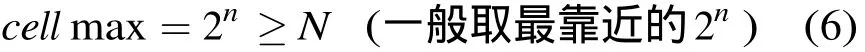
其中

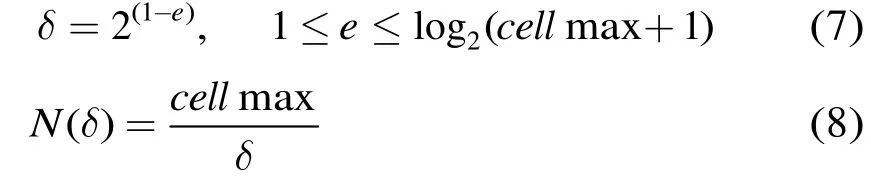
由式(5)-式(8)，即可求得分形维数 fd。

2.2 幅度调制特征识别原理

对于不同目标，目标雷达回波的起伏特性具有差异，而幅度调制可以很好地表征回波幅度的特性，故提取回波序列的幅度调制特征作为识别特征之一：

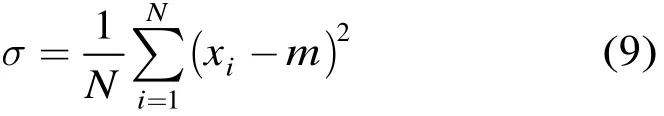
式中，xi为雷达回波序列，N为含有目标距离门的回波点数，

由于这样的幅度调制存在幅度的敏感性，将幅度调制进行归一化处理。

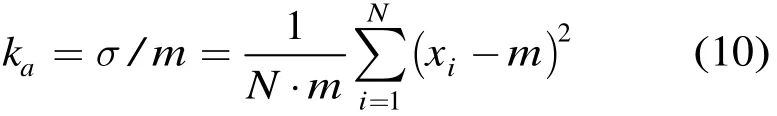
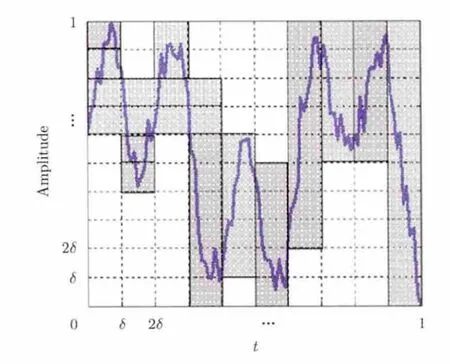
图1 盒维数计算示例Fig.1 Box dimension example

3 实验结果和讨论

3.1 特征提取与分析

为了验证所提算法的有效性，本文基于机载火控雷达实测同一场景下的不同时间多个试飞架次数据进行验证，试飞目标均为直升机、螺旋桨飞机、喷气式飞机3类目标。目标均为与雷达迎头方向飞行的目标，因为往往机载雷达更加关注迎头威胁目标。提取的是目标跟踪且CFAR检测过门限的目标点，目标跟踪外推的点(非检测点)将不予考虑，提取的目标的信噪比在15 dB以上，距离在200～260 km之间。

图2给出的是特征提取和分类识别流程图，由流程图可知，基于窄带“和通道”数据，进行脉冲压缩和相干积累，提取目标的窄带分形特征和幅度调制特征。图3给出的是3类飞机的分形特征的统计分布，图5给出的是3类飞机的幅度调制特征统计分布。

由图3可知，直升机、螺旋桨飞机、喷气式飞机的分形特征具有差异性，直升机的分形维数范围为(1.33, 1.65)，螺旋桨飞机的分形维数范围为(1.22,1.55)，喷气式飞机的分形维数范围为(1.22, 1.44)，因此存在重叠区域，由于基于的是特征统计分布，3类目标的大多数统计的分形特征还是具有较明显的差异。此外由图3可知，直升机和螺旋桨飞机比喷气式战斗机的分形维数要大，这是因为直升机和螺旋桨飞机表面粗糙程度和不规则程度比喷气式战斗机的要大，这与实际情况相符。

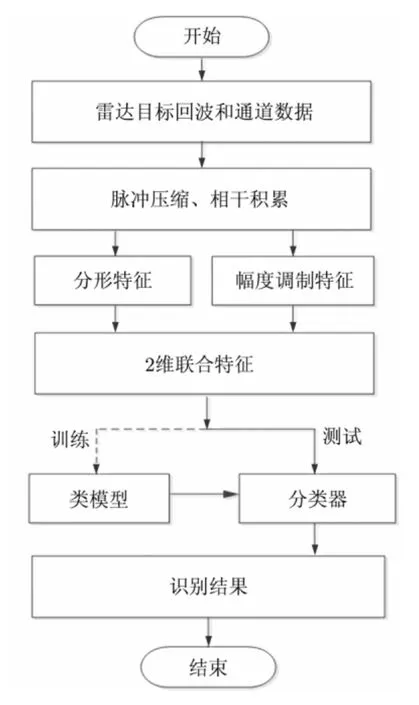
图2 基于分形和幅度调制特征的机载雷达飞机目标分类流程图Fig.2 Airborne radar aircraft target classification based on fractal and amplitude modulation features

图4给出的是直升机、螺旋桨飞机和喷气式飞机的幅度调制特征的统计特性，由图 4(a)-图 4(c)可知，3类飞机的窄带幅度调制特征分布具有明显的差异性，尤其是直升机、螺旋桨飞机和喷气式飞机的幅度调制特征具有较明显的差异，而直升机和螺旋桨飞机的的幅度调制特征数值较大，即回波幅度波动较大，说明飞机旋转部件的调制分量在整个回波中占据较大的成分，表明飞机旋转部件在飞机结构中是显著的，如螺旋桨飞机和直升机，反之，对于喷气式飞机，回波中以平稳的机身分量为主，飞机旋转部件结构比飞机机身小得多，这与实际情况相符。

图5给出的是直升机、螺旋桨飞机和喷气式飞机的分形特征和幅度调制特征的2维分布，由图5可知，3类飞机的 2维特征分布还是具有较明显的差异，如喷气式飞机在分形维数和幅度调制特征的起伏范围相对较小，而螺旋桨飞机次之，直升机起伏最大。

3.2 识别结果及分析

在本文分类识别过程中，支持向量机(SVM)训练样本为当前架次的3个飞机特征数据中随机抽取100个，基于SVM训练后的分类线对另一试飞架次的测试数据进行分类(两个试飞架次相互独立，目标为相同的3种飞机目标)。再基于SVM给出分类识别结果并对识别结果进行修正。图6给出了基于分形和幅度调制特征的分类识别结果，3种不同飞机占据的特征分别为A区，B区和C区，由图6可知，基于分形和幅度调制的2维特征可以有效地将直升机、螺旋桨飞机和喷气式飞机进行分类识别，分类识别正确率分别92%(螺旋桨飞机)，89%(直升机)，97%(喷气式飞机)，3类飞机目标平均分类识别率为92.67%。

4 结论

本文在机载雷达目标分类识别需求牵引下，同时考虑到当前机载雷达普遍具有窄带跟踪模式，提出了基于窄带分形和幅度调制特征的机载雷达飞机目标分类识别技术。在试飞数据基础上进行分析验证，试验结果验证了本文算法的有效性和稳健性，直升机、螺旋桨飞机、喷气式飞机的平均分类识别率在87%以上，同时还得出以下结论：

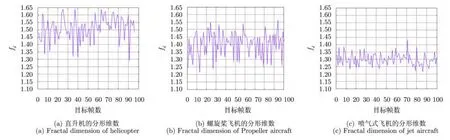
图3 3类飞机的分形特征fdFig.3 Fractal feature fd of three kinds of aircraft

图4 3类飞机的幅度调制特征kaFig.4 Amplitude modulation ka of three kinds of aircraft

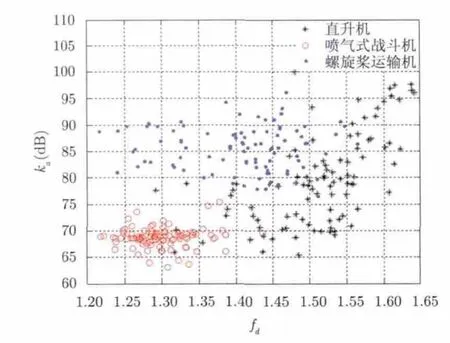
图5 3类飞机的分形和幅度调制2维特征分布Fig.5 Fractal and amplitude modulation feature distribution of three kinds of aircraft

图6 基于分形和幅度调制特征的3类飞机目标分类识别结果Fig.6 Three kinds of aircraft classification results based on fractal and amplitude modulation features

(1) 当前试飞架次的分类结果可以作为另一个试飞架次的分类模板，试飞架次之间相对独立，分类结果有效，体现了算法的稳健性；

(2) 直升机和螺旋桨飞机的分形维数明显比喷气式飞机的分形维数起伏范围大；

(3) 直升机和螺旋桨飞机的幅度调制特征比喷气式飞机的幅度调制特征的起伏范围大，直升机的幅度调制特征起伏为 30 dB，螺旋桨飞机的幅度调制特征起伏为 15 dB，喷气式飞机幅度调制起伏范围最小，起伏为10 dB；

(4) 计算量较小，耗费雷达资源少，在窄带模式下，100点训练样本就有较好的分类识别结果，便于工程实现。

[1]Tait P.Introduction to Radar Target Recognition[M].UK:the Institution of Electrical Engineers, 2005: 8-10.

[2]Du L, Liu H, and Wang P.Noise robust radar HRRP target recognition based on multitask factor analysis with small training data size[J].IEEE Transactions on Signal Processing, 2012, 60(7): 3546-3559.

[3]王鹏辉, 刘宏伟, 杜兰, 等.基于线性动态模型的雷达高分辨距离像小样本目标识别方法[J].电子与信息学报, 2012, 34(2):305-311.Wang Peng-hui, Liu Hong-wei, Du Lan, et al..Linear dynamic model based radar HRRP target recognition under small training set conditions[J].Journal of Electronics &Information Technology, 2012, 34(2): 305-311.

[4]Toumi A, Khenchaf A, and Hoeltzener B.A retrieval system from inverse synthetic aperture radar images: application to radar target recognition[J].Information Sciences, 2012,196(1): 73-96.

[5]Yuan Bin, Chen Zeng-ping, and Xu Shi-you.Micro-doppler analysis and separation based on complex local mean decomposition for aircraft with fast-rotating parts in ISAR imaging[J].IEEE Transactions on Geoscience and Remote Sensing, 2014, 52(2): 1285-1298.

[6]Chamberlain, N E, Walton, E K, and Garber F D.Radar target identification of aircraft using polarization-diverse features[J].IEEE Transactions on Aerospace and Electronic Systems, 1991, 27(1): 58-67.

[7]Du L, Wang B, Li Y, et al..Robust classification scheme for airplane targets with low resolution radar based on EMD-CLEAN feature extraction method[J].IEE E Sensors Journal, 2013, 13(12): 4648-4662.

[8]Bell M R and Grubbs R A.JEM modeling and measurement for radar target identification[J].IEEE Transactions on Aerospace and Electronic Systems, 1993, 29(1): 73-87.

[9]Skolnik M I.Radar Handbook[M].Third Edition,McGraw-Hill Companies Incorpration, 2010: 197-198.

[10]Chen X, Guan J, and He Y.Detection of low observable moving target in sea clutter via fractal characteristics[J].IET Radar, Sonar & Navigation, 2013, 7(6): 635-651.

[11]王福友, 郭汝江, 郝明, 等.基于分形特征的地杂波背景下的球载雷达目标检测方法[P].国防发明专利, 授理号:201110015890.X.Wang Fu-you, Guo Ru-jiang, Hao Ming, et al..Balloon borne radar target detection within ground clutter based on fractal character[P].National Defense Invention Patent, Accepted no.201110015890.X.

[12]Iodice A, Natale A, and Riccio D.Kirchhoff scattering from fractal and classical rough surfaces: physical interpretation[J].IEEE Transactions on Antennas and Propagation, 2013,61(4): 2156-2163.

[13]Perna S and Iodice A.An algorithm for efficient and effective evaluation of scattering from fractal surfaces[J].IEEE Transactions on Geoscience and Remote Sensing, 2012, 50(9):3554-3566.

[14]Evans R, Bennett J G, and Jones J.The evaluation of fractal surfaces for modeling radar backgrounds[R].AD, 2007,7(ADA457965/XAB): 1-27.

[15]Potapov A A, German V A, and Grachev V I.“Nano -” and radar signal processing: fractal reconstruction complicated images, signals and radar backgrounds based on fractal labyrinths[C].201314th International Radar Symposium,German, 2013, 2: 941-946.

[16]Li Qiu-sheng and Xie Wei-xin.Multifractal modeling of aircraft echoes from low-resolution radars[C].IET International Radar Conference, Xi’an, China, 2013,DOI:10.1049/CP.2013.0396.

[17]Chang C and Chatterjee S.Fractal based approach to shape description, reconstruction and classification[C].Twenty-Third Asilomar Conference on Signals, Systems and Computers, California, USA, 1989, 1: 172-176.

[18]Potlapalli H and Luo R C.Fractal-based classification of natural textures[J].IE E E T ran sa ctio ns o n Ind u stria lElectronics, 1998, 45(1): 142-150.

[19]Popescu A L, Popescu D, and Ionescu R T.Efficient fractal method for texture classification[C].International Conference on Systems and Computer Science, Kansas City, USA, 2013,2: 44-49.

[20]Mishra A K, Feng H, and Mulgrew B.Fractal feature based radar signal classification[C].IET International Conference on Radar Systems, Edinburgh, UK, 2007, 2: 1-4.

[21]Zlatintsi A and Maragos P.Multiscale fractal analysis of musical instrument signals with application to recognition[J].IEEE Transactions on Audio, Speech, and Language Processing, 2013, 21(4): 737-748.

[22]Salmasi M and Hashemi M M.Design and analysis of fractal detector for high resolution radars[J].Chaos, Solitons and Fractals, 2009, 40: 2133-2145.

[23]Eryildirim A, Onaran I, and Etin A E.Pulse Doppler radar target recognition using a two-stage SVM procedure[J].IEEE Transactions on Aerospace and Electronic Systems, 2011,47(2): 1450-1457.