弱测量问题的信息处理方法初探

胡卫东

(国防科技大学ATR重点实验室 长沙 410073)

1 引言

当前的许多军用探测系统因为受到成本、布站范围、传感器灵敏度与时效性等因素的限制，与“透明化”的需求相去甚远，除了遭遇干扰、欺骗等对抗环境之外，经常面临的信息获取困难也制约了其探测的性能。其中低信噪比、低数据率、低分辨率和低测量维度的“四低问题”是目标探测信息处理面临的共性难点问题。这里将其统称为“弱测量”问题(不同于量子力学中不扰动被测系统的弱测量的概念)。在弱测量条件下，目标的状态和属性能否有效估计，该问题的研究具有重要的理论和实际意义。

2 弱测量问题的提出

弱测量条件主要由目标的暴露征候和传感器的性能所决定，目标的暴露征候弱通常称之为低可观测，传感器的性能受限称之为低信息获取能力。弱测量对信号的检测和参数估计等信息处理能力提出了严峻的挑战，具体表现为以下4个方面：

(1) 低信噪比。这种情况最容易理解，出现的典型情况主要有两种：一种是被测目标落在传感器感受范围内的特性很弱，比如隐身目标对雷达来说其反射的电磁信号难以探测到；二是被测目标背景影响较大，比如超视距雷达工作的环境，由于超视距雷达分辨单元相比所关注的目标大得多，由分辨单元中环境引入的噪声能量就很大。再比如水下目标的远距离探测，水声的多途传播降低了水下目标的可探测性。

(2) 低数据率。出现的典型情况也有两种：一种是传感器探测目标的频度很低，比如单颗低轨卫星对某一地域进行照相侦察，由于卫星重访同一地域的时间间隔较长(1天到几天的频度)，对运动目标监视来说，其抽样频度过低。另一种是目标可被探测时间较短，比如利用雷达探测潜艇的潜望镜，一般潜艇上浮使用潜望镜的时间较短，大部分时间都潜在水下。这种情况也造成获取目标的数据率低下。

(3) 低分辨率。低分辨率主要指在空间遇到难以分辨的问题，出现的典型情况也有两种：个体辨识和群体分辨。特别是在群目标探测的情况下，个体信息丢失严重。比如用远程预警雷达难以分辨突防的弹道导弹和伴飞的诱饵。另一方面，低分辨也会导致信息相关的错误发生，比如 ESM[1]对电磁辐射源探测的信息，因空间分辨差导致在目标密集情况下很难与高精度的目标定位信息建立相关关系。

(4) 低测量维度。首先我们所处的空间确定 1个运动点的位置需要1维时间和3维空间数据来表征。而我们使用的传感器因为是通过感受目标所发射、反射或辐射的物理场信号来工作的，物理场信号与时空的对应性不一定会很强，比如靠感受发射或辐射信号的装置通常较难测量距离。其次，目标属性的确定因其描述的复杂性，需要更高维度的测量。但实际中往往难以做到，只能得到某个部分、某一侧面的观测。另一方面，就测量量本身来说，与属性量也可能存在低关联度的问题。例如依据舰艇尾迹的探测推断舰艇的属性。

上述问题是长期困扰侦察监视系统设计和使用的老大难问题，这些问题的本质是缺少可用信息量，导致传统基于高效信息更新的“急功近利”式处理方法难有用武之地。例如对运动目标状态的估计，我们习惯于传感器测量量与目标状态之间具有紧耦合的对应关系，比如雷达测量的距离和角度是目标所处的坐标位置的合理表达方式。一旦测量量与被测对象的状态不具有良好的对应关系时，传统的如卡尔曼滤波等信息更新方法将难以应用。此外，随着大数据时代的到来，所面临的数据价值密度低的问题，无论是数据中信息含量少(就像矿石含某种贵重金属品位低一样)，还是无效数据多(存在大量空巢现象)，本质上也是弱测量问题。弱测量条件虽然不足以支持直接检测发现目标或状态估计，不等于说测量获得的信号没有信息量，关键看信息如何利用。因此，对这类问题解决方法的思考具有重要的指导和借鉴意义。

3 弱测量问题的解决思路

弱测量问题因为表现形式多样，使得最初的解决方法起始于局部的特定问题的探讨，比如微弱信号的检测，弱小目标的跟踪、密集目标条件的数据关联、低分辨条件下的目标辨识等等，由此发展出了检测前跟踪、知识辅助的信号与信息处理、随机有限集、似然函数理论等多种多样的理论与方法。其基本思想是充分利用可用信息，包括相关知识，然后设计某种准则下的优化模型。

实际上，从测量信息与被测对象的关系出发，我们更容易看清该类问题的本质，传统的测量属于强耦合测量，关于被测对象的信息含量大，可信度高，因此，采用基于信息的模型更新更多地依赖当前测量量的作用，其典型代表就是卡尔曼滤波器，通过持续不断地加入观测信息进行模型修正，达到准确估计目标运动状态的目的。但是当我们所关注的被测对象为弱小目标、分布式目标或者群目标的时候，传统的测量系统受到物理条件的限制(如能量、分辨力、灵敏度等)，关于被测目标获取的信息无法给予直接的支持，传感器测量量与被测对象的状态不再具有较好的相容性，而沦为“弱测量”的地位。

既然弱测量的直接表现是可用信息含量少，因此，解决弱测量的基础就是实现信息的有效集合。即通过量变的积累，实现由量变到质变。具体来说，大量贡献微弱(不精确、不清晰、不完整)的信息如何关于被测对象相关集合在一起，这就是“弱测量”理论的核心。而信息集合的基本依据是被测对象的属性或变化样式反映在弱测量信息中具有确定规律可循，该规律最基本的表现方式一是不断重复出现，二是具有可预见性，最终使得被测对象的行为可追溯。

3.1 “重复性”是最直接的可利用规律

物理学在双缝干涉实验中，光子的波动性就是靠大量光子不断重复同样的传播行为而获得[2]。在宏观世界这种情况也比比皆是。人类按照工业文明产生的技术标准，规模化地创造自己世界的过程中，重复地使用所发现和掌握的规律/工艺，使得“重复出现”的行为特点成为必然。在应用层面同样如此。比如空间轨道目标的环绕运行方式可以视为一个沿椭圆轨道不断重复的行为；飞机平时的例行侦查，其沿固定航线的飞行是一个不断重复的行为；脉冲雷达发射的信号也是一个不断重复的工作模式；这种例子举不胜举。只要被测对象的特性从观测角度来看是可以不断重复的，即使每次测量获取的信息再少，也能因为被测对象的重复行为而实现测量信息的有效集合，这就是弱测量理论解决被测对象特性估计问题的前提条件。

从数学来看，可重复性一般表现为确定形式的重复性和统计意义上的重复性。重复保证了信息积累的可行性，弱化了时间起点的影响。确定形式的重复性意味着类似周期特性的函数，对一个周期内函数特性的估计可以采用各种准则、各种基函数族的逼近办法，这依赖于对函数特性的了解程度。当然，可重复的行为并非一定可用严谨的数学模型来量化，其它描述方式同样可遵循上述原则来处理。

统计意义上的重复性在实际中已产生了很多具体的处理方法。最直观的例子就是侦收电文的破译，其主要思路就是通过字母出现的频度检查，统计寻找字母表中的字母在构成词汇时存在的“重复性”[3]。在信号处理领域，比如对雷达信号的侦测、分选，大量采用了循环平稳信号处理方法[4]，以充分利用侦收信号在统计上的重复性(相关性)；对低信噪比信号提取的背越效应[5]，就是利用了微弱信号重复性的统计变化规律，将其叠加在已知的大信号上，以抬升到采样灵敏度门限以上。在微波频段实现量子雷达[6]，也属于典型的弱测量问题。目标特性引起的电磁波动方面的量子涨落非常微弱，只有充分利用大量光子在统计特性上的一致性通过长时间积累才能有所显现。

3.2 “可预见性”具有更大的应用潜力

不断重复的行为是一种严格的约束条件，放宽到“按照可预计的规律变化”也是成立的。因为可预测，所以可以通过补偿变化趋势而再次呈现不断重复的特点。

由于按标准化方式运作，自动化在很大程度上表现为程序规定的一系列动作，很多时候甚至只需要一点点提示就能推知全貌。比如卫星发射一般是按照基本物理定律和程序进行的，以何种方式入轨都清清楚楚，这时只需要知道很少的信息就能做出准确的判断。这就产生了所谓的可预见性。

目标特性的可预测性是解决“弱测量”问题的重要基础。特别是对于低维度观测问题来说，被测对象特性散布于高维度的空间中，但它的行为特点则因其可预见性而减少了描述的维度，比如卫星轨道存在于3维空间，但描述轨道的椭圆却只有2维。基于此，对高维度来说的低维(缺维)观测有可能解决本质上是低维度上的形态估计。单站只测角系统定轨就是一个很好的例子，只能测量2维角度量(方位、俯仰/赤经、赤纬)随时间变化的序列，利用轨道力学的可预测性，就可以估计出人造卫星/小行星体现在高维度空间中的轨道运动形态。

目标环境特性的可预见性同样重要。例如对于水下目标探测来说，如果能根据水下环境参数(温度、盐度、密度、水下地形等)预测水声信道的传播状态，尽管水声信号传播路径复杂，但可以根据预测的传播特性反演目标真实的水声信号，能够明显提高水下探测能力。

值得说明的是，弱测量问题不仅体现在直接状态信息的测量，也体现在具有相关性的属性测量方面，比如微观粒子存在纠缠关系，则对其中一个粒子的测量可以推断出另一个粒子的行为。这种纠缠所导致的可预见性是量子传感应用的基础。

4 弱测量问题的求解—贝叶斯理论

当被测对象不再可直接观测，运用统计学直接获得被测对象的特性变得不可能的时候，贝叶斯理论为我们提供了新的解决思路。

“贝叶斯公式是可以支配一切知识、一切信息的法则。”加拿大普里美特理论物理研究所Fuchs的评价[7]虽然有些极端，但弱测量问题确实可以利用贝叶斯统计法来解决。当我们深入到弱测量领域，不难得出以下结论：由于测不准，被观测对象的存在状态只能用概率的形式描述；简而言之，为了能够准确地描述关注目标的运动，状态估计成了一片“概率”云。随着直接信息的缺失，不知不觉中，信息加工变成了只是对观测者掌握信息状态的描述。正如在微观世界我们之所以看到粒子运动怪诞离奇，只是因为我们无法掌握相关信息的全貌。这就是贝叶斯统计！

下面我们以目标跟踪问题为例说明贝叶斯理论的重要性。当我们无法获得高信噪比的准确信息时，我们需要应用似然性原理，更新操作在统计分布层面来完成。

目标跟踪问题可看作是对目标运动状态的估计过程，运动状态一般包括位置、速度、加速度等，有时也包括特征信息(如雷达散射截面、阻力系数等)。为后续分析方便，我们作以下假设和定义[8]：(1)目标的运动服从马尔科夫过程，(2)传感器的似然函数只依赖于观测时刻目标的状态。

传感器：每种传感器可能有不同的量测空间，假设我们知道传感器物理效应转化的概率分布，则对这种传感器的似然函数就可确定下来。当然传感器关于目标状态s的响应可以是线性的或非线性的，概率分布可以是高斯或非高斯的。

似然函数：假设我们在观测时间 0≤ t1≤…≤ tk≤ t 构成的序列为 Yk，令 yk为随机变量 Yk的取值。似然函数可表示为：

假设目标在各时刻的状态为 s1, s2,… , sK，观测量取值记为 y = (y1, y2,… , yK)，定义观测时间内的联合似然函数为：

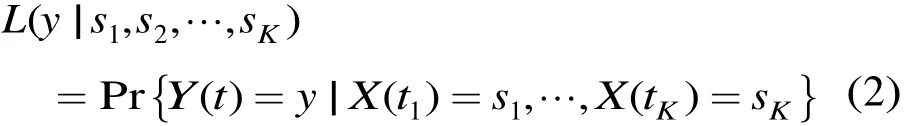
定义先验概率：

为随机过程{X( t); t ≥ 0}的先验概率，前面讲到的重复性和可预见性则体现在其中。

根据贝叶斯理论，目标状态的后验概率分布如下：

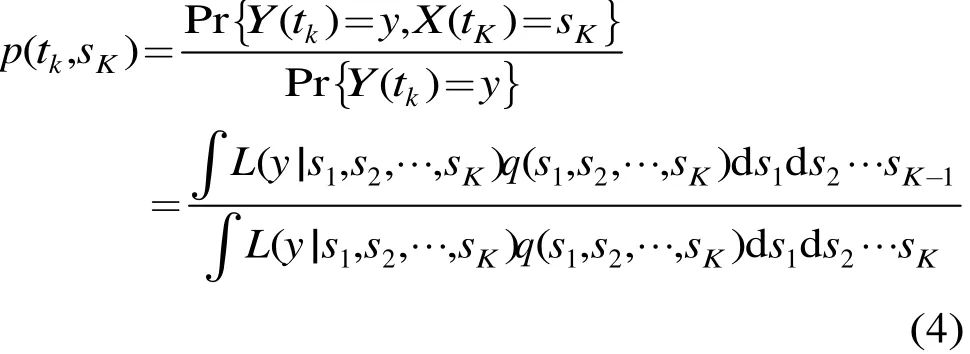
式(4)在随机过程{X( t); t ≥ 0}为马尔科夫过程的假设下，可以采用如下递推方式来求解：

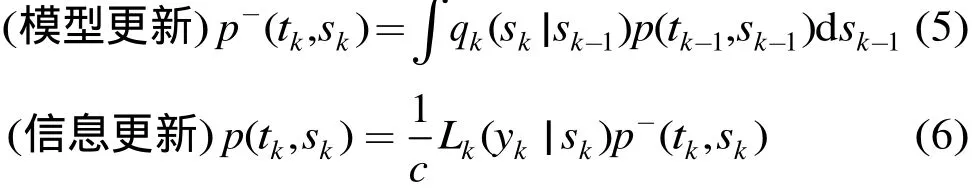
我们看到，由于短时间内获取的信息极为有限，对目标状态或属性的推断存在较大的不确定性，只能从似然性的角度度量和整合新信息，表现为弱测量导致的从信号到状态空间的似然函数统计分布的构建，以及目标状态统计分布的演化，以代替常规的状态量本身的更新，这是贝叶斯理论解决弱测量问题的基本出发点。另外，状态转移的先验概率也充分体现了可预见性指导下对运动模型知识的利用。

5 弱测量对信息系统设计的要求

当我们希望对大范围区域(如全球)事无巨细都能全局掌控时，弱测量问题就具有一定的普遍性。它必然对侦察监视信息系统中的传感、处理和控制提出新的要求。

5.1 对传感器设计的要求

随着可利用电磁频谱的扩展和武器平台运载能力的提高，广域监视能力的需求更加迫切，导致了泛探概念及相应传感系统的产生[9]，典型的如射电天文望远镜，海军舰艇上的集成桅杆等。它们都要求在时间、空间和频谱上的宽覆盖能力。过去在窄信道条件下，我们追求的是较少的观测次数和更高的精度。而泛探系统在目标搜索发现阶段不可避免地面临低信噪比、低精度观测的问题。因为在时间、空间和频谱任一维度上拓展能力都需要付出代价，比如制作宽频带天线，受到材料和工艺的限制，常常以牺牲天线增益来换取频带宽度，天线增益的损失相当于降低了接收信号的信噪比。因此，该类系统必然面临海量数据但平均信息含量低下的问题。这使得泛探系统的平衡设计成为关键。

5.2 对信息处理的要求

正如现在的电子侦察设备一样，泛探系统首先实现宽口径的海量数据采集，信息的提取完全靠后期的处理来完成。其处理过程有点像翻砂淘金的筛选、挖掘方式，以计算资源的消耗为代价。对于实际应用来说，一些处理需要保证时效性，比如目标跟踪中的状态估计；另一些处理则可以有所滞后，比如情报分析。不同的需求导致信息处理流程设计上必须按照轻重缓急进行任务分解，以对应不同的计算资源。具体来说，对于时效性强的任务，通过扩展计算资源，如增加计算节点，换取时间的缩短；对于精度要求高的任务，则通过扩展时间资源积累更多的信息来解决；即设备换时间，时间换精度。进一步，按时效性划分的处理级别并不是孤立的，后续的每一级处理都应该是对前一级处理的复核和深化。通过这种逐级渐进的方式减缓海量数据的处理压力，处理的时间资源得到了扩展，保证了泛探系统存在的“采集快处理慢”的问题得到解决。

5.3 对系统控制的要求

弱测量除了在似然分布层面操作而对计算量有更苛刻的要求外，信息获取的方式同样需要新的设计理念。信息系统一般根据任务流程来规划控制流程和信息处理流程，通过控制得到的反馈信息越准确，信息处理就越简单。因此，有目的的采集信息，实现控制与数据获取的有机协调是解决弱测量问题的基本保证。特别是在监视阶段，利用可预见性的特点，传感器按照目标可预测的行为进行数据采集，比如在必经的路径上等待目标的出现。

弱测量条件下，很难保证目标信息在短时间内被提取出来，因此，时效性强的闭环控制难以完成(比如传统目标跟踪回路的闭合是建立在即时准确提取信号偏差信息基础上的)。但信息系统不能盲目地进行工作，试图遍历所有的可能性，信息的反馈是系统有效性的基本要素，这就导致系统设计必须从单一功能回路的闭环扩展到整个系统更大的任务层面闭环反馈控制上来，即扩展反馈控制的范围与尺度，从保证即时状态的更新扩展到在更大时间范围内提取到目标状态的可用信息。

6 总结

随着人类对物质和能量的驾驭能力越来越强，产生弱测量的情况会更加普遍。从信息获取的角度看，由低可观测演变为低信息质量；从信息处理的角度看，由基于测量数据直接进行物理量的推演，转变为把测量数据看作物理量统计分布的抽样过程；从系统控制角度看，由单一功能短程回路的闭环控制转变为整个系统任务层面的长程反馈控制。这反映了解决弱测量问题的信息系统在设计实现上的变化趋势。在这类信息系统设计上，只有善于运用空间的腾挪和问题的转化，比如通过时间、空间、频谱乃至计算等资源的互换与转化，才能有效规避传统上单一资源或物理域面临的瓶颈问题，在更广阔的范围内找到问题求解的方法。

[1]Davies C L and Hollands H.Automatic processing for ESM[J].IEE Proceedings F Communications, Radar and Signal Process, 1982, 129(3): 164-171.

[2]关洪.量子力学基础[M].北京: 高等教育出版社, 2000: 12-14.Guan Hong.Basic Quantum Mechanics[M].Beijing: Higher Education Press, 2000: 12-14.

[3]John Keegan.Intelligence in War[M].Canada: Vintage Canada, 2004.

[4]黄知涛, 周一宇, 姜文利.循环平稳信号处理与应用[M].北京: 科学出版社, 2006.Huang Zhi-tao, Zhou Yi-yu, and Jiang Wen-li.Cyclostationary Signal Processing and its Application[M].Beijing: Science Press, 2006.

[5]朱贵岭.超微弱信号通过 A/D 变换器的背越效应及检测[C].第八届全国雷达学术年会论文集, 2006: 651-656.Zhu Gui-ling.Carrying effect and the detection in the super micro weak signal passing A/D converter[C].Proceedings of 8th National Radar Conference, 2006: 651-656.

[6]Lanzagorta M and Radar Q.Synthesis Lectures on Quantum Computing[M].USA: Morgan & Claypool Publishers, 2012:66-67.

[7]Fondez M, Ikonicoff R, 等.王佳, 译.揭秘世界的方程式[J].新发现Science & Vie, 2013, (2): 28-45.Fondez M, Ikonicoff R, et al..Wang Jia Translation.Equation of revealing the world[J].New Discovery Science & Vie, 2013,(2): 28-45.

[8]Stone L D, Barlow C A, and Corwin T L.Bayesian Multiple Target Tracking[M].MA Norwood: Artech House, 1999: 57-61.

[9]汤小为, 汤俊, 彭应宁, 等.一种新体制雷达—“泛探”雷达的关键技术研究[C].第十届全国雷达学术年会论文集, 2008:43-46.Tang Xiao-wei, Tang Jun, Peng Ying-ning, et al..Research on some key techniques of a new radar system: ubiquitous radar[C].Proceedings of 10th National Radar Conference,2008: 43-46.