IEC火花试验装置的电容短路放电特性数学仿真分析

钟久明，刘树林，崔 强

(1．西安科技大学电气与控制工程学院，陕西 西安710054;2．海南师范大学物理与电子工程学院，海南 海口571158)

1 引言

目前运用IEC火花试验装置的爆炸性试验是电路本质安全(简称本安)性能最直接的检测方法，但该方法操作复杂、需时较长［1］，且只能在少数几家防爆检验机构进行。该方法不能随时指导本安产品的设计和制造，延长了产品研制周期、增加了成本、制约了产品的推广应用。因此迫切需要建立本安防爆电路的非爆炸评价系统，进行相关的研究具有重要的理论意义与实用价值［2，3］。

电路本安性能评价主要考虑电感开路或电容短路时的故障能量，因此建立基于安全火花试验装置，能描述电感电路分断与电容电路短路放电特性的数学模型，是构建非爆炸本安评价系统的基础。

目前对电感分断放电研究较多，也建立了一些较实用的电弧放电数学模型［3，4］;而对电容短路放电的研究主要集中在最小点燃电压、电路本安参数的选取等［5，6］、点燃能量的测量［7］、容性电路短路放电的引燃特性［8，9］以及电容放电对开关型本质安全电源影响及其参数设计等［10-13］。

对其放电数学模型的研究还比较少。文献［14］提出了容性电路输出短路火花放电的电压、电流和功率函数。但是，运用火花试验装置对电容电路进行开闭环实验表明，其放电电压和电流曲线与实验结果存在较大的偏差，可见所得出的函数关系并不能全面地反映容性电路短路放电的电压和电流特性。文献［15］针对简单电容电路，提出了一些短路放电特性的指数函数模型，但所提模型无法得到放电时间、放电功率与放电能量等关键参数的定量描述，不能全面反映容性电路短路放电伏安特性。

作者在大量实验的基础上获得了电容短路放电的典型伏安特性曲线，发现了维持电压、维持时间等重要放电特征参量，但是现有文献报道尚不能解释这一现象，也没有建立相应数学模型，更没有得出引燃能力与相关因素的关系表达式，从而制约了非爆炸性本安判据的获取。

本文基于IEC标准的安全火花试验装置，对电容电路进行大量短路放电实验研究，用示波器采集典型放电电流、电压波形，基于场致发射的原理建立了电容电路短路放电的数学模型，为本安电路非爆炸评价系统的建立奠定了理论基础。

2 电容短路放电特性

简单电容电路短路放电原理如图1所示。其中，U为电源电压，R1为充电电阻，R2为放电回路的总电阻，C为被试电容，G为安全火花试验装置，电容两端分别连接钨丝和镉盘电极，两电极以约25cm/s的速率短路［1］。uG和iG分别为放电电压和电流。典型放电电流和电压曲线如图2所示，根据图2，电容电路短路放电过程可分一次放电、电压维持及二次放电三个阶段。

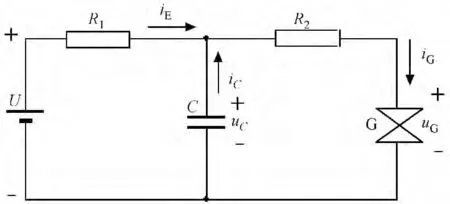
图1 简单电容电路短路放电试验电路Fig．1 Scheme circuit of simple capacitive circuit short-circuit discharge experiment

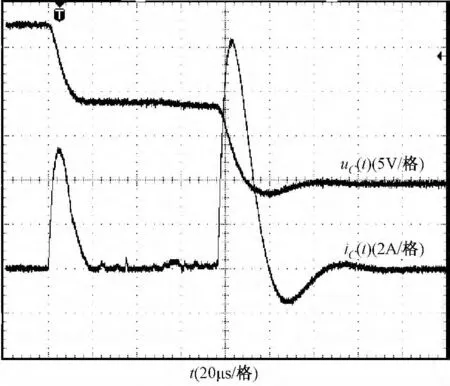
图2 实测试验波形(V i=18V，C=12μF，R1=560Ω)Fig．2 Short-circuit discharge experimental waveforms

当电极运动至放电间隙对应的临界击穿间距时，间隙达到临界击穿场强，间隙被击穿，称为一次击穿。期间电极间距不断减小，极间场强不断增大，放电电流迅速增大，从而导致电容两端电压迅速下降并使极间场强减小，当极间场强的增大(间距缩短)与减小因素(电压下降)达到平衡时，放电电流达到最大值，此后由于电容电荷的泄放，电容电压的不断下降，电极间距减小而使极间场强的增大已无法平衡极间电压下降而使极间场强的减小，因而极间场强迅速下降并很快小于临界击穿场强，从而使得放电电流从峰值迅速下降并接近于零。此后，由于极间场强小于临界击穿场强、间隙恢复绝缘，放电电流近似为零，电容储存电荷近似于零泄放，电容两端电压(亦即极间电压)近似维持不变，称为电压维持阶段。而后，随着电极间距的逐渐减小至另一临界击穿间距时，气体被再次击穿，称为二次击穿，其放电电流及电压的变化规律类似一次放电。

可见，在一定输入电压下，电容短路放电过程中出现维持电压和维持时间等特征参量。下面将根据实验获得的典型放电电压、电流波形，运用曲线拟合的方法建立放电数学模型并对其放电伏安特性进行分析。

3 电容短路的气体放电数学模型

气体放电从总体上包括电极上和气体中两类基本过程。从气体放电引燃爆炸性气体的角度出发，关注的是电极上的行为。下面将以阴极电流和极间电压为参量，建立IEC标准火花试验电容短路放电的数学模型。

3.1 放电电流的数学模型

由图2可知，电容短路放电引燃爆炸性气体的能量主要来源于一次放电和二次放电。下面首先针对一次放电的伏安特性进行数学分析。

考虑到正离子的漂移速度远小于电子的漂移速度，因此仅考虑阴极的电子发射电流。

在安全火花试验中，光发射、次级发射均只能形成极微小的发射电流，故可忽略。

火花试验装置的打火机构由高熔点金属钨丝和低熔点金属镉盘组成。在进行火花试验时，无论用钨丝还是镉盘作为阴极，示波器所测得的阴极放电电流基本一致，故可忽略热发射而认为场发射是其主导发射机制。

Fowler-Nordheim通过解薛定谔方程获得的场致发射电流密度为［16］其中，E0为阴极表面电场强度;Φ为阴极逸出功;常数A=1.54×10－6/Φ;B=6.83×107×Φ1/3。

在火花放电期间，极间电场是关于时间的函数，而且其变化规律与sin(t)在第一象限的变化类似，故式(1)中的E02项可用sin(t)替代，而式(1)指数项中的E0项可用时间变量t代替，并用系数来校正其误差。假设阴极截面积为定常数，并考虑到电容电路放电的持续时间大约为几十微秒［9］，为便于计算，可设放电电流表达式为

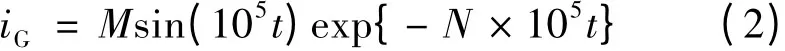
在图1所示的放电试验电路中，由于R2≪R1，故短路放电期间，可忽略电源对放电间隙的影响［1］，因此，其放电试验的简化电路如图3所示。

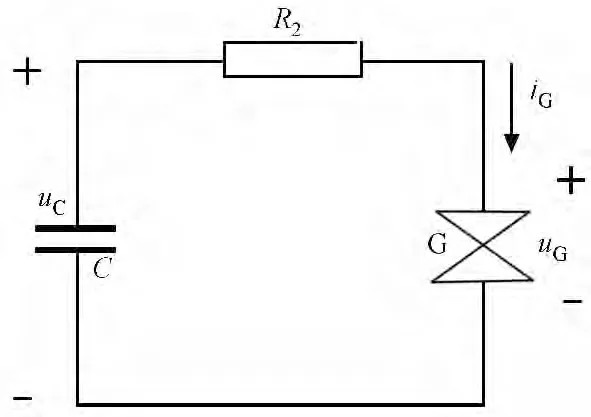
图3 电容电路短路放电简化电路Fig．3 Simplified circuit of simple capacitive circuit short-circuit discharge experiment

根据图3，可列出电路方程将式(2)代入式(4)，并利用分部积分可得

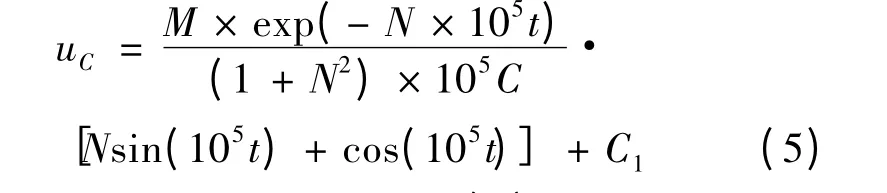
代入初始条件:t=0时，uC(0)=U，其中U为电源电压，可得积分常数C1=U－M×10－5/C(1+N2)，将其代入式(5)并结合式(2)和式(3)，可得其中，P=M×10－5/［C(1+N2)］;Q=N－R2C(1+N2)×105。

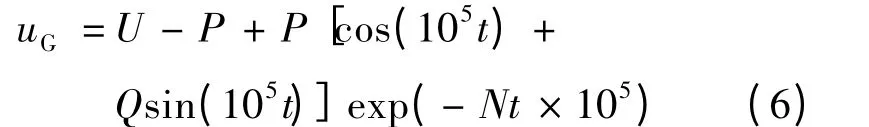
可见，只要确定式(2)和式(6)中的系数M和N，便可得出电容电路短路放电过程中一次放电的放电电流及电压的时域表达式，即放电间隙的伏安特性便可确定。因此，从电路原理上，可将火花放电间隙等效为一非线性阻抗。这一电路模型的获得为容性电路本安特性的非爆炸评价奠定了基础。

3.2 数学模型的参数确定

设一次放电时间为TG。根据第3.1节分析，当t=TG时，放电电流iG(TG)=ε，其中ε足够小。将该边界条件代入式(2)，可得

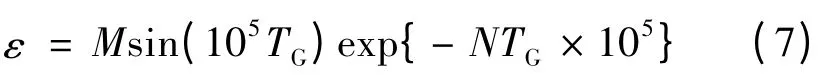
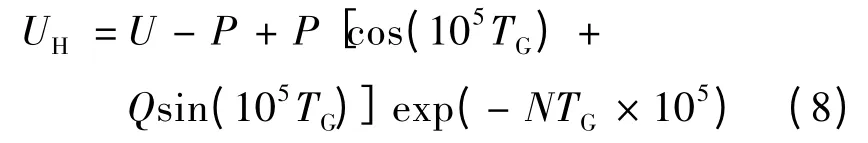
同理，当t=TG时，uG(TG)=UH，其中UH为维持电压。将该边界条件代入式(6)，可得可见，式(7)和式(8)中除M、N外均为设定或给定电路参数。由此不难算出其中的未知参数M、N，从而一次放电电流和电压的函数便可确定。

对于二次放电伏安特性的数学分析与一次放电的分析方法类似。假设二次放电的放电电流为其中，t'=(t-TG-TH)×105;TG、TH分别为一次放电和电压维持时间;M'、N'为待定系数，其确定方法类似于参数M、N的确定方法，参见式(7)和式(8)。

由于放电的随机性，放电时间TG、TH及T'G为统计参数，其值取决于电路参数，如输入电压U和电容C等，可由实验方法来确定，大致方法如下:

针对同一电容(取C=16.8μF)，依次取不同初始电压分别进行十次短路试验，取其平均值为最终结果。运用Matlab对实验数据进行曲线一次拟合并综合考虑电容初始电压与电容值两因素后可得一次放电时间与电容初始电压的关系为维持时间TH与电容及其初始电压的统计函数关系为其中，U为电容初始电压，单位为V;C的单位为μF;TG的单位为μs。

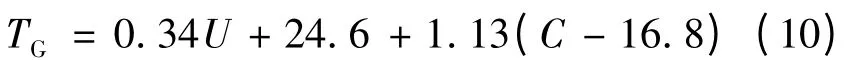
二次放电时间T'G的初始电压为维持电压(10V)，其放电时间主要取决于电容。类似地，运用实验与曲线拟合的方法可得

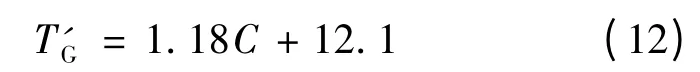
可见，给定电容值、初始电压及维持电压，一次放电时间TG、维持时间TH及二次放电T'G时间均可确定，从而易得一次及二次放电电流、电压时域表达式。一次及二次放电火花是电容电路短路的主要引燃源，因此，放电伏安特性的获得，为容性电路的非爆炸本安评价奠定了理论基础。

4 实例和实验

给定电路参数:电容C=12μF，电容初始充电电压U=18V，维持电压取为UH=10V，火花装置内阻取为R2=0.2Ω。设定强制参数ε=0.2A。代入式(10)，可得一次放电时间为TG=25.3μs。同理，根据式(11)和式(12)可得维持时间TH=55μs以及二次放电时间T'G=26.3μs，则TG+TH=80.3μs。

将以上给定参数代入式(7)、式(8)，联立解之可得M=44.9，N=1.9，P=8，Q=0.8。将M、N、P及Q代入式(2)和式(6)可得放电电流和电压的表达式分别为

同理，将上述参数代入式(11)、式(12)，联立解之可得M'=52.8，N'=1.9，P'=10，Q'=0.8。将M'、N'、P'及Q'代入式(7)和式(8)，令t'=(t－80.3)×10－6，可得二次放电电流和电压的表达式分别为运用Matlab对式(13)～式(16)进行数学仿真分析，可得放电电流和电压波形如图4所示。

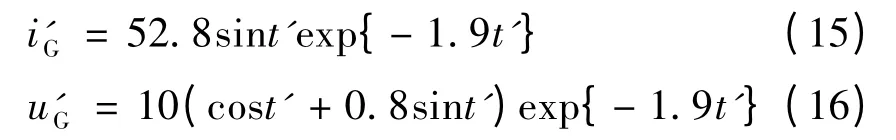
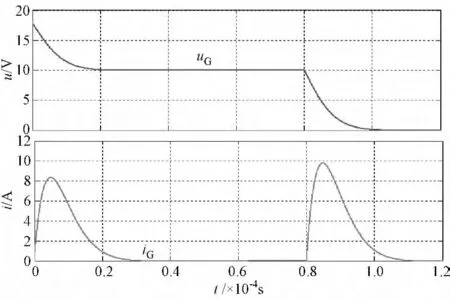
图4 放电电流、电压仿真波形Fig．4 Simulation waveforms of discharge current and voltage

对比图4的仿真波形与图2的实验波形可看出，在电容短路放电期间，放电电流、电压的仿真波形与实验波形吻合得很好，只是仿真电流的峰值比实验波形的要略大一些，同时放电时间比实测时间也要略长一些。这主要是由于放电时间通过实验数据的拟合函数进行计算，而实测放电时间，一方面由于放电的随机性，其本身具有一定的分散性，另一方面，放电时间以电流下降到某一微小值为截止时刻，所以通过示波器观测数据时也存在较大的读数误差。

事实上，由于模型的峰值电流及放电时间均比实验值略高一些，从而使得仿真模型的放电能量要比实验测量值略高一些，而这反而使得仿真模型具有更高的安全性能。

可见，所提出的电路模型不仅能够模拟电容短路放电发展的物理过程，放电电流、电压的变化趋势完全与理论分析吻合并与实验一致，且模型具有更高的安全性能。

为验证数学模型的正确性及实用性，运用VB程序语言设计并开发了一款针对简单电容电路的本质安全性能非爆炸评价仿真器，如图5所示。

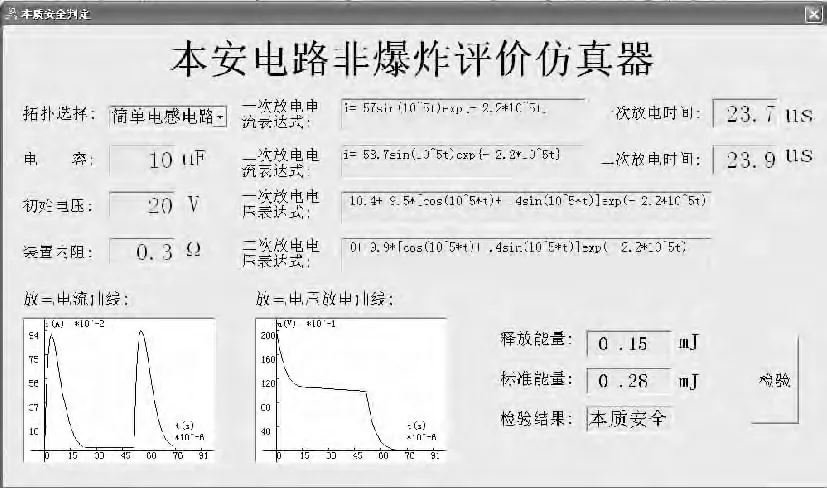
图5 本安电路非爆炸评价仿真器Fig．5 Intrinsic safe circuit non-explosive evaluator

运用IEC标准安全火花试验装置对仿真器评价结果进行比对测试，大量测试结果表明，通过选择适当的有效能量修正系数(本实验中设为0.1)，仿真评价器的评价结果具有足够的可靠性。

需指出的是，尽管该仿真评价器仅能对简单电容电路的本安防爆性能进行评价，但是该研究对电路本安性能非爆炸评价方法及实现进行了有益的探索，为本安电路非爆炸评价体系的建立奠定了理论基础。

5 结论

将IEC安全火花试验装置的简单电容电路短路放电过程分为一次放电、火花维持及二次放电三个阶段。建立了一次及二次放电电流的时域模型:iG=M sin(105t)exp{－N×105t}，给出了待定参数M、N的计算方法。

提出了一款本安电路非爆炸评价仿真器的设计方法，仿真与实验结果表明所建模型的正确性及电容电路非爆炸本安评价的可行性与可靠性。

仿真模型的建立为电路的非爆炸本安评价及计算机评价系统的建立奠定了理论基础。

［1］中国强制性国家标准汇编(Chinesemandatory national standards compilation)［M］．电工卷(Electrical Par)，GB 3846.4—2000．北京:中国标准出版社(Beijing:China Standard Press)，2003．

［2］刘树林，刘健(Liu Shulin，Liu Jian)．本质安全开关变换器(Intrinsically safe switching converters)［M］．北京:科学出版社(Beijing:Science Press)，2008．

［3］孟庆海，胡天禄，牟龙华(Meng Qinghai，Hu Tianlu，Mu Longhua)．低能电弧放电时间与电路参数间的关系(Relationship between discharge time of low energy arc and circuit parameters)［J］．电工技术学报(Transactions of China Electrotechnical Society)，2000，15(4):19-21．

［4］孟庆海，牟龙华，王崇林，等(Meng Qinghai，Mu Longhua，Wang Chonglin，et al．)．基于线性衰减模型分析低能电弧放电特性(Analysis of low energy arc discharge characteristics based on linear current attenuationmodel)［J］．煤炭学报(Journal of China Coal Society)，2001，26(6):654-656．

［5］商立群，施围(Shang Liqun，ShiWei)．安全火花电路的放电形式和电感电路放电时间的测量(The discharge forms of intrinsic safety spark circuitand themeasurement of the discharge times of inductance circuit)［J］．煤 矿安全(Safety in Coal Mines)，2004，35(6):36-38．

［6］Sean Clarke．Basic techniques of intrinsically safe circuit assessment［J］．Electrotechnology，1999，2(8):43-46．

［7］D Oancea，Domnina Razus，V Munteanu，et al．High voltage and break spark ignition of propylene/airmixtures at various initial pressures［J］．Journal of Loss Prevention in the Process Industries，2003，(16):353-361．

［8］张国军(Zhang Guojun)．容性本安电路短路放电瞬时火花引燃爆炸性气体的研究(Research on ignition of explosive gases by capacitive intrinsic safety short-circuit discharge instantaneous spark)［J］．电气防爆(Electric Explosion Protection)，2001，(3):25-29．

［9］穆丽娟(Mu Lijuan)．电容放电对开关型本质安全电源影响的研究(The research about the impactof capacitive discharge in switching intrinsically safe power supply)［J］．真空电子技术(Vacuum Electronics)，2010，(6):60-63．

［10］刘树林，刘健(Liu Shulin，Liu Jian)．本质安全Boost变换器的非爆炸内部本质安全判据(Non-explosive inner-intrinsic safety criterion of intrinsic safe Boost converter)［J］．煤炭学报(Journal of China Coal Society)，2008，33(6):707-712．

［11］Liu Shulin，Liu Jian，Yang Yinlin，etal．Analysis of output short-circuit discharged energy and optimal design of output intrinsically safe Buck converters［A］．Proceedings of Asia Pacific Symposium on Safety［C］．Shaoxing，China，2005.1978-1984．

［12］刘树林，刘健，寇蕾(Liu Shulin，Liu Jian，Kou Lei)．开关变换器的本质安全特性分析与设计(Intrinsically safe behavior of switching converters and its design)［J］．电工技术学报(Transactions of China Electrotechnical Society)，2006，21(5):36-41．

［13］刘健，刘树林，杨银玲，等(Liu Jian，Liu Shulin，Yang Yinling，et al．)．Buck变换器的输出本质安全特性分析及设计(Output intrinsically safe behavior of Buck converters and its design)［J］．中国电机工程学报(Proceedings of the CSEE)，2005，25(19):52-57．

［14］章良海，宋雅婷(Zhang Lianghai，Song Yating)．安全火花原理及应用(The principle and application of the safe spark)［M］．北京:煤炭工业出版社(Beijing:Coal Industry Press)，1984．

［15］刘建华(Liu Jianhua)．爆炸性气体环境下本质安全电路放电理论及非爆炸评价方法的研究(Study on intrinsically safe circuit discharge theory in explosive gas environment and its non-explosive evaluating method)［D］．徐州:中国矿业大学(Xuzhou:China University of Mining＆Technology)，2008.

［16］徐学基，诸定昌(Xu Xueji，Zhu Dingchang)．气体放电物理(Gas discharge physics)［M］．上海:复旦大学出版社(Shanghai:Press of Fudan University)，1996．