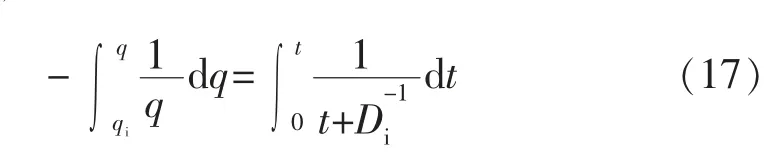Arps递减微分方程的推导及应用
2014-06-17陈元千郝明强
陈元千,郝明强
(中国石油勘探开发研究院,北京100083)
1945年,Arps[1-2]通过定义损失比(Loss ratio)参数,对油井实际产量递减数据进行统计分析,并在未经推导的情况下提出了一个常微分方程。在此基础上,首创性建立了指数、双曲、调和3 种递减模型,受到学界的高度重视,并被世界各石油公司和储量价值评估公司广泛应用于产量和可采储量预测。笔者在此方面通过长期深入研究,也取得了一些成果[3-16]。本文应用文献[3]的研究成果,对Arps 微分方程进行了理论推导。
1 Arps 微分方程的推导
Arps 递减率为单位时间的产量变化率[1-2],表示为

式中:D 为递减率,月-1或a-1;q 为递减阶段产量,m3/月或104m3/a;t 为生产时间,月或a。
由此,Arps 初始递减率Di可相应表示为[2]
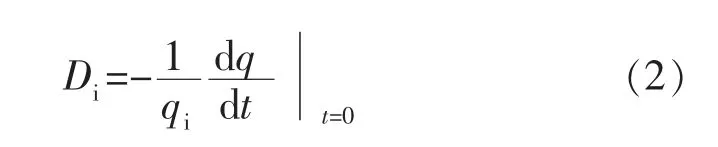
式中:qi为初始阶段产量,m3/月或104m3/a。文献[3]给出递减率与时间的关系式为
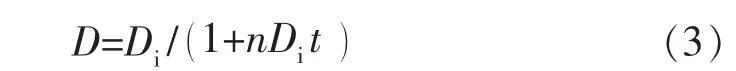
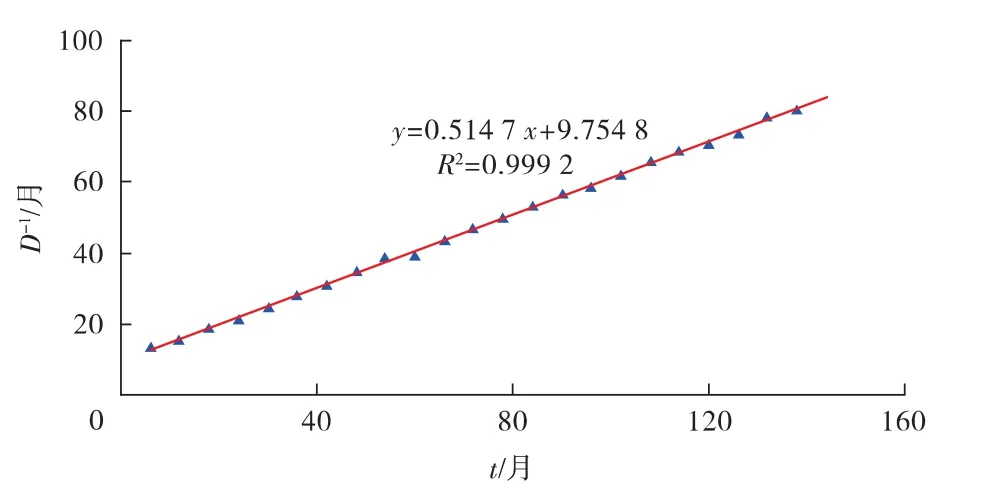
式中:n 为递减指数,取值[0,1],n=0 时产量为指数递减,0 对式(3)两边求倒数后,得出 实际数据[1]表明D-1-t 呈直线关系(见图1),相关系数高达0.999 2,这证明了式(4)的正确性。 图1 D-1-t 关系曲线 对式(4)两边关于t 进行求导,得 式(5)清晰地展现了递减指数n 的含义。将式(1)代入式(5),即可得出与Arps 相同的二阶常微分方程: 对式(6)两边积分,得到Arps 一阶常微分方程为 式中:c 为积分常数。 当t=0 时,q=qi,由式(7)得 结合式(2),得 将式(9)与式(7)结合,可得 式(10)也可由式(4)结合式(1)直接得出,式(5)—式(7)的推导过程便于理解Arps 微分方程的由来。 在Arps 微分方程基础上,在[0,1]区间假定不同的n 值,由式(10)求解得出Arps 的3 种递减模型。 当n=0 时,可将式(10)改写为 对式(11)求倒数,并关于q,t 分离变量积分,得到 对式(12)求积、简化,得到Arps 指数递减模型为 当0 对式(14)求积并整理,得到Arps 双曲递减模型为 当n=1 时,由式(10)可得 对式(16)进行分离变量积分,得到 对式(17)求积并整理,得到Arps 调和递减模型为 [1]Arps J J.Analysis of decline curve[J].Trans.A.I.M.E.,1945(160):228-247. [2]Arps J J.Estimation of primary oil reserves[J].Trans.A.I.M.E.,1956(207):182-186. [3]陈元千.双曲递减分析的一个简单方法[J].天然气工业,1989,9(2):24-27. [4]陈元千.油气藏工程计算方法[M].北京:石油工业出版社,1990:223-227. [5]陈元千,李璗.现代油藏工程[M].北京:石油工业出版社,2001:127-161. [6]陈元千.确定递减类型的新方法[J].石油学报,1990,11(1):74-80. [7]陈元千.确定定容气藏递减类型的新方法[J].石油勘探与开发,1984,11(3):52-59. [8]陈元千.常数百分递减的分析[J].天然气工业,1986,6(1):47-50. [9]陈元千.判断油田递减类型的新式典型曲线图[J].中国海上油气(地质),1993,7(6):33-39. [10]胡建国,吴剑霞,陈元千.产量递减分析的典型曲线图[J].新疆石油地质,1993,14(2):147-151. [11]陈元千.双曲线递减的简化及确定可采储量的截距法[J].天然气工业,1994,14(4):32-37. [12]陈元千.利用递减参数确定可采储量的方法[J].石油勘探与开发,1994,21(3):95-98. [13]陈元千.广义的КОПЫТОВ公式及其应用[J].石油勘探与开发,1991,18(1):56-61. [14]陈元千,胡建国.新型递减曲线方程的推导及应用[J].新疆石油地质,1992,13(3):251-256. [15]陈元千.预测油气田可采储量和剩余可采储量的快速方法[J].新疆石油地质,2005,26(5):544-548. [16]陈元千,王孝金,程继荣,等.适用于海外合作开发油田预测可采储量、产量和储采比的方法[J].中国海上油气,2011,23(6):380-383.

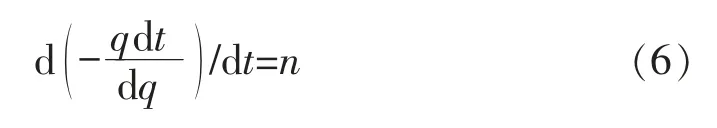




2 Arps 微分方程的应用
2.1 指数递减模型

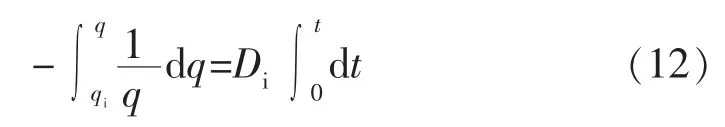

2.2 双曲递减模型
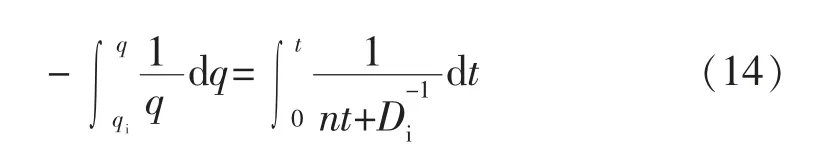

2.3 调和递减模型