基于博弈论的不平衡报价分析及控制

闫 晶，刘星宇

（常熟理工学院 经济与管理学院，江苏 常熟 215500）

博弈论起源于20世纪初，1944年冯·诺依曼和奥斯卡·摩根斯顿合著的《博弈论和经济行为》奠定了博弈论的理论基础。博弈必备的四个要素是博弈的参与者、博弈规则、参与者选择的行为或策略、参与者的收益。博弈论就是研究决策主体在给定信息情况下如何决策以最大化自己的效用，以及如何实现不同主体决策之间的均衡。招投标作为国际上普遍采用的一种交易方式，是一种规范化的竞争手段。在建筑工程招投标竞争中，各投标人的根本利益是相互冲突的，竞标行为是相互影响的，因此，招投标过程实质上是众多利益方的博弈过程。

目前，我国的工程招投标普遍采用的是工程量清单招标模式，实行量价分离、风险共担的原则，招标人追求的是在确保工程质量和工期的前提下，工程造价最小化，对所提供的清单的准确性负责，承担量的风险；投标人则根据自己的企业定额或市场价格信息自主报价，承担价的风险。投标人为了企业利润的最大化，在投标报价中往往根据招标项目的具体情况采用多种策略，其中，不平衡报价策略的应用最广泛。

不平衡报价策略是指在投标报价时，投标人在保证总报价不变的前提下，有意识地改变某些分项工程的正常价格，即提高某些分项工程的单价，再降低另一些分项工程的单价[1]43，以期在不影响中标的情况下，得到更理想的经济效益的策略。从博弈的角度看，这是一种零和博弈，投标人额外获得的经济效益，正是招标人所蒙受的经济损失。

适当的不平衡报价可以增加投标人的经济效益，提高投标人的项目管理水平；严重的不平衡报价则会使中标人的结算价远远高于中标价，增加招标人的工程成本，影响招标人的利益。因此，对严重不平衡报价进行控制是很有必要的。

一、不平衡报价产生的原因及超额利润模型

不平衡报价产生的主要原因可归结为招、投标方利益相悖、采用工程量清单计价模式、招标文件及设计文件存在缺陷等，如图1所示。

投标人通过不平衡报价策略的采用，有助于企业获得超额利润，保证企业利润最大化目标的实现。不平衡报价一般有两种类型，一类为前重后轻法，即“早收钱法”；另一类为因量调价法，即“多收钱法”。

（一）前重后轻法超额利润模型

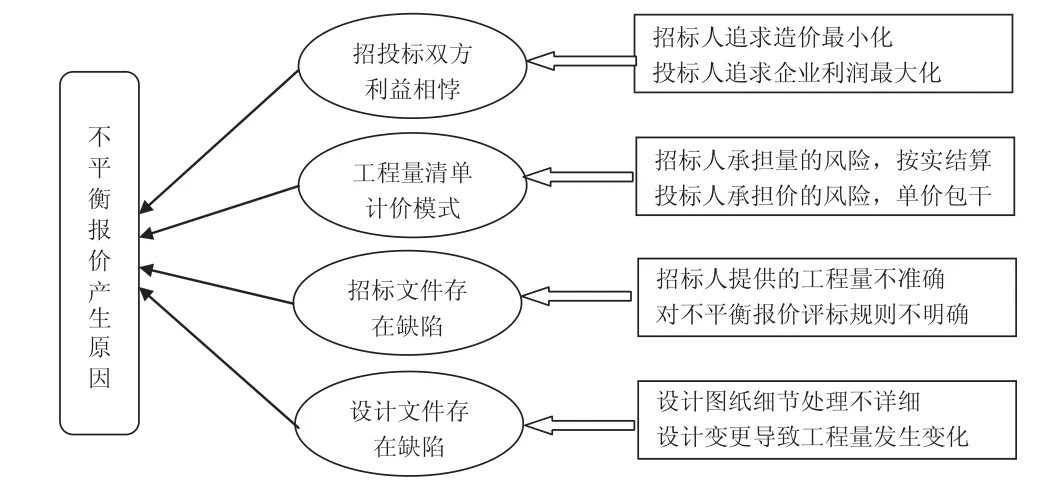
图1 不平衡报价产生的主要原因

前重后轻法是投标人根据实际经验，对投标项目进行具体分析，对于先施工的项目提高其报价，对于后施工的项目降低其报价，从而在保证总造价不变的情况下，充分发挥资金的时间价值，使企业提前收到比正常额度高的工程款，减轻企业垫付工程款的压力。

若Qi为某工程招标文件中第i个分项工程的清单工程量，pi和pi′分别为第i个分项工程的正常报价和不平衡报价的综合单价，根据不平衡报价前后各分项工程量不变，且总报价相等的原则，存在等式关系，等式左右两侧数值之和即为投标报价，亦表示投标人中标后应完成的总产值。该产值一般以月或季度为发生周期，待工期结束，产值即全部完成，累计完成产值如图2所示，图中实线表示正常报价时产值完成情况，虚线表示不平衡报价时产值完成情况。从图2可以看出，不平衡报价时累计完成产值图的形心比正常情况报价时的形心前移。因中标人所完成的产值即为发包人付款的基础，故通过前重后轻法策略的应用，中标人能够实现提前收到工程款以降低资金压力的目的。

图2 产值完成对比示意图

另外，假设Tsi和Tfi分别为第i个分项工程的开始时间和完成时间，令△t=Tfi-Tsi，则单位时间周期内完成的工程造价分别为 A=Qi*Pi/Δt、A'=Qi*Pi'/Δt，考虑资金的时间价值后正常报价及不平衡报价的现值NPV1、NPV2计算公式分别为：

由公式（1）可以看出，超额利润与分项工程总造价及开始时间成正比，与完成该分项工程所需时间成反比。

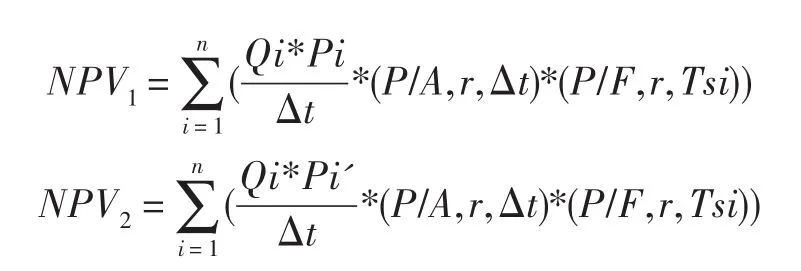
（二）因量调价法超额利润模型

因量调价法是投标人通过研究设计图纸，并根据以往施工经验预测某些分项工程量的变化趋势，在保持总报价不变的情况下，调高预测工程量将增加的分项工程综合单价，降低预测工程量将减少的分项工程综合单价，此时工程量变化幅度越大，价格调整幅度也越大。

若Qi′为预测工程量将增加的分项工程实际工程量，Qj′为预测工程量将减少的分项工程实际工程量，Pi′、Pj′分别为不平衡报价的综合单价，则投标人采用不平衡报价能够获得的超额利润计算公式为：

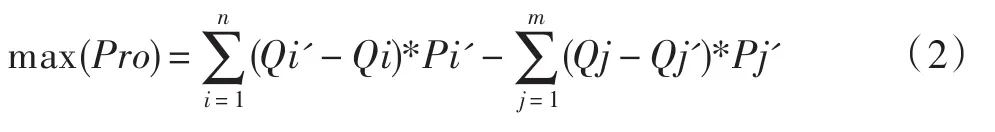
由公式（2）可看出，超额利润与预测工程量将增加的幅度及综合单价成正比，与预测工程量将减少的幅度及综合单价成反比。

二、不平衡报价中的博弈分析

招投标过程中通常有一个招标方和多个投标方，哪个投标人中标不只受投标人自身投标策略的影响，也受到参与各方投标策略的影响，即哪个投标人能中标是所有参与竞争的投标人共同决策的结果。

在投标过程中，理性的投标人会在争取中标的同时努力实现利益最大化，假定两个投标人A和B采用不平衡报价可获得超额收益max（Pro），此时属于完全信息的静态博弈，投标人间的博弈矩阵模型见表1。

博弈矩阵模型的均衡解为（max（Pro），max（Pro）），即投标人博弈结果是大家均采用不平衡报价法。

在不平衡报价过程中，各投标人同时作出报价决策，且只了解投标人自身的成本状况及报价策略，而不知道其他投标人的成本状况及报价策略。因此，不平衡报价过程实际上是一个不完全信息的静态博弈，其对应的均衡解为贝叶斯纳什均衡。

假设工程项目的正常投资成本为C，Cmin和Cmax分别为该工程的最低和最高成本，C∈[Cmin，Cmax]，Ci是第i个投标人的成本，bi是第i个投标人的报价，若其中标，则中标人的收益为ui＝bi-ci。根据贝叶斯纳什均衡理论有：

投标人的主要目的是使ui最大化，对以上方程求极值，先对上式求一阶导数得：

Φn-1(b)+(b-c)(n-1)Φn-2(b)Φ'(b)=0

简化后为：Φ(b)+(b-c)(n-1)Φ'(b)=0

在投标人报价策略均衡情况下，Φ(b)=λc，式中λ为大于等于1的常数，则上式可写成：

方程两边积分后得：

ln((1-n)(x-1)-x)=ln λc+ln a

式中a为常数，则：(1-n)(x-1)-x=λac

将x＝b/c代入上式，整理得贝叶斯纳什均衡通解：

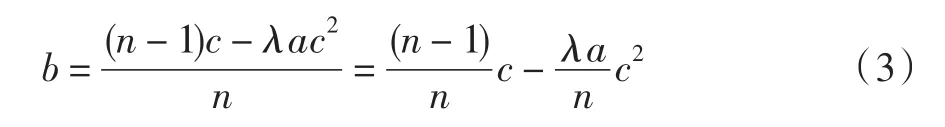
从公式（3）的均衡解可以看出，b随n的增大而增大，特别是当n→∞时，b→c。也就是说，投标人越多，各投标人的报价就越趋近于企业的真实成本，招标人就越能够得到最优的报价。

三、不平衡报价控制路径

通过对投标人超额利润模型及博弈分析可知，不平衡报价策略虽是投标过程中投标人普遍采用的策略，但采用适当的方式可以规避招标人的风险，并降低不平衡报价策略对招标人造成的利益损失。主要方式有：①挖掘招投标隐性主体，适度转移风险；②细化不平衡报价的评审方法；③探索招投标新模式。

（一）挖掘招投标隐性主体，适度转移风险

从公式（3）可以得出投标人数量的增加能够减小报价与实际成本的差距，使投标人的报价更趋于其真实成本，使中标价格更低。采用公开招标方式招标可以吸引更多的投标人参与工程投标，投标人与投标人之间的博弈更加充分，可使业主资金得到最优化利用。

从公式（2）看投标人能否实现“多收钱”，关键取决于实际工程量是否与工程量清单中的工程量存在较大差异，而这种差异的出现存在两种可能情况：一是工程量清单本身存在误差，二是施工过程中出现设计变更。第一种情况的责任主体是造价咨询公司，第二种情况的责任主体是设计公司，因此，在招投标过程中，实际参与的主体除了招标人、投标人之外，还有造价咨询公司和设计公司，前两个主体是显性的，而后两个主体是隐性的，但正是隐性的主体为投标方不平衡报价的采用创造了条件。为了减小招标方利益损失，博弈的参与者不应只限于招投标双方之间，还应包含咨询公司及设计公司。

为了最大限度地减少由于设计变更引起的工程量增加，招标人在委托设计时应与设计公司约定设计变更控制幅度及变更项目，实际变更超出约定幅度时，超出部分给招标人带来的额外损失由设计公司共同承担。为了提高工程量清单编制的准确性，招标人在委托工程量清单编制时应与咨询公司约定：在原图纸范围内，结算时实际工程量与清单工程量超出一定范围外给招标人带来额外损失时，由咨询公司共同承担相应损失。由于参与者的增加，以及博弈规则的明

λc∂b+(b-c)(n-1)λ∂c=0确，不平衡报价风险被适度转移，招标人的利益可得到更好的保障。

表1 投标人A、B博弈矩阵模型[2]112

（二）细化不平衡报价的评审方法

博弈规则是博弈的四大要素之一，美国普林斯顿大学数学家塔克于1950年提出“囚徒的困境”是西方理论界最具代表性的博弈案例，也非常明显地体现了博弈规则在博弈过程中的重要性。在该案例中假设有两人联合入室盗窃，警察抓住他们后，在两个不同的房间进行隔离审讯，两人则无法串供。审讯时警察对两人均坦白、只有一人坦白、两人均抵赖三种情况的判刑方法进行了详细告之。此时因为无法串供，每人都将认真思考另外一方可能的行为，从而决定自己的行为策略。基于每人做出的决策可能产生的最终结果思考，最终两人都坦白了自己的行为。

从上例可以看出，博弈最重要的假设前提是“人是理性的”，两个以上的理性决策主体按照预先设定的规则进行策略选择，使决策参与者的自身利益最大化。在招投标过程中，招标人与投标人都有各自的利益目标，招标人目的是通过招投标过程选择质量好、价格合理的承包人，而投标人的目的是通过投标获取承包项目及相应利润。投标人为了使自身利益最大化，在投标报价过程中可能采用不平衡报价策略。为适当减小该策略给招标人带来的利益影响，应从评标方法入手对不平衡报价进行限定，比如以招标控制价为基准设定适当的上下限，当某分项工程投标报价比控制价低或高于该幅度时即为不平衡报价，同时设定一个不平衡报价的绝对额度，根据各投标人出现不平衡报价额度的高低扣减不同分值。此时投标人为了降低被扣分值或不被扣分，提高中标几率，则会尽可能使不平衡报价额度低于其他投标人，或将投标报价控制在规定的范围内，从而减小招标人的利益损失。投标人合理控制不平衡报价幅度同样能够实现早收钱、多收钱的目的。该种评标规则充分考虑了招投标双方的利益，既存在投标人与招标人的博弈，也存在投标人与投标人之间的博弈。

（三）探索招投标新模式

目前我国建设工程招投标主要是以招标控制价为基准确定投标报价上下限，根据投标人报价进行评审，选择合理低价者中标或综合得分最高者中标。该种模式投标人可以利用招投标双方之间信息的不对称，隐藏其真实心理价格，并通过不平衡报价，获得尽可能多的利润，对招标人的利益带来了潜在影响。针对此种模式存在的问题，可引入第二价格密封拍卖模式。

第二价格密封拍卖是由维克里教授首先提出的。维克里运用信息经济学原理设计了一种新的拍卖机制，即潜在卖家以密封的书面形式出价，商品售给所报价格最高的竞标者，但实际确定的价格是出价第二高的竞标人的报价，这种拍卖机制能够使竞拍者报出真实价格。[4]138

招投标过程实质是第二价格密封拍卖的逆向形式，在这种情况下，投标人采用高于真实心理价格的报价则可能会失去中标机会，采用低于真实心理价格的报价则可能承受亏损，投标人本着趋利避损的动机往往会按照其真实心理价格来报价。同时投标人在报价过程中若采用不平衡报价策略对自身的利益不会带来有益影响，因而投标人会禀着真实、合理的原则进行报价，减少不平衡报价出现的概率。这种模式可以使招标人由被动变为主动，选择到合适的承包商，并有效地优化资源配置。

四、结 论

通过对招投标过程中投标人采用不平衡报价策略实现企业利益最大化的原因、利润模型及不平衡报价时的博弈的分析，能够发现其中存在招标人与投标人之间的博弈、投标人与投标人之间的博弈以及招标人与设计公司、咨询公司之间的潜在博弈。为减小不平衡报价给招标人带来较大的利益损失，在招投标过程中可以将风险适度转移给博弈的隐性参与主体――设计公司及咨询公司，细化评标方法中对不平衡报价的评审规则，采用第二价格密封拍卖等招投标新模式。

[1]汪建栋.浅议建设单位如何应对工程量清单不平衡报价[J].建筑经济，2012（5）.

[2]宋志勇.不平衡报价的量化识别与博弈研究[J].西安建筑科技大学学报（自然科学版），2012（2）.

[3]饶海琴，徐彩红.政府投资项目中的不完全信息静态博弈模型分析[J].上海理工大学学报，2006（4）.

[4]诚然，吴文升，孙卓睿.第二价格密封拍卖理论框架下政府投资项目招投标模式改进研究[J].工业技术经济，2011（3）.