水下圆柱壳振动与声辐射低频等效计算方法

唐锐，商德江，李琪（哈尔滨工程大学水声技术实验室，哈尔滨150001）

水下圆柱壳振动与声辐射低频等效计算方法

唐锐，商德江，李琪
（哈尔滨工程大学水声技术实验室，哈尔滨150001）

为了提高水下大长径比圆柱壳低频振动响应和辐射声功率的计算效率，该文提出了一种用水下梁模型等效计算的方法。该等效模型基于欧拉梁理论，采用附加水质量近似流固耦合作用，通过计算梁的等效杨氏模量系数，使其与圆柱壳的梁式弯曲振动模态对应。计算表明，对大长径比简支圆柱薄壳（L/a＞20），等效梁杨氏模量系数主要取决于结构长径比，而厚度对其的影响甚小。文中还给出了不同长径比圆柱壳前五阶模态频率的等效杨氏模量系数曲线，利用梁模型并结合此曲线，可准确预报水下圆柱壳低频域辐射声功率和圆柱壳的梁式弯曲振动模态。

圆柱壳；振动；声辐射；欧拉梁；等效杨氏模量系数

equivalent Young’smodulus coefficients

1 引言

潜艇、鱼雷等水下有限长圆柱壳声振特性的解析和数值计算方法，由于流固耦合作用而比较复杂[1]，为了提高计算效率，水下大长径比圆柱壳声振特性的低频等效算法得到了关注[2]。由于大长径比圆柱壳的低频振动特性与梁结构类似，其低频声辐射特性主要决定于梁式振动模态。如果能采取某种合适的等效方法将圆柱壳模型等效为简单的梁模型，则可快速计算辐射声功率。Forsberg[3]研究了在空气中采用梁式弯曲振动模态计算圆柱壳振动的应用条件，对于细长（长径比L/a＞20）薄壳，应用简单梁理论预测了圆柱壳的弯曲振动模式（n=1）的最低模态频率和振型，并分析了不同边界条件的影响。梁模型若只考虑一维的横向位移，忽略与其它方向位移间的耦合作用，就只能准确预报圆柱壳梁式弯曲振动的第一阶模态频率，高阶模态频率偏差较大。值得指出的是，Forsberg通过计算发现，对于长径比L/a＞20的薄壳，只要周向半波长和轴向半波长均远大于壳体厚度，半径与厚度比（a/h）在满足20＜a/h＜100时，不同径厚比对弯曲振动模态（n=1）影响甚小，也就是说此时细长薄壳弯曲振动模态与弯曲刚度无关。对于梁声辐射问题的研究，Sun[4]采用传递矩阵法计算分析了空气中不同边界条件下的均匀梁和非均匀梁的振动响应及辐射声功率与辐射效率。考虑水介质与梁结构的耦合作用，Wallace[5]研究了带无限长障板的有限长梁的声辐射问题，推导了梁的辐射阻的渐进解，并得出在简支和固支边界下，辐射阻随着宽长比增大而升高。借鉴船体振动理论[6]，采用附加水质量近似流固耦合作用的方法，可以将结构水下低频振动与声场分开计算[7]。这样针对水中结构，可以采用空气中常用的模态叠加法[8]、差分变化法[9]、传递矩阵法[4]等方法计算梁的振动响应，并将计算得到的结构水下振动响应代入到声场计算公式中计算声场。本文通过研究水下大长径比（L/a＞20）有限长圆柱薄壳的声辐射特性发现，水下圆柱壳低频声辐射特性主要决定于圆柱壳梁式振动模态（n=1），进而提出了应用等效杨氏模量系数，采用水下梁模型等效计算水下圆柱壳低频域辐射声功率的方法，拓展了文献[3]中应用简单梁理论预报圆柱壳振动特性的应用范围，并通过实例验证了方法的有效性。

2 理论模型

对于大长径比（L/a＞20）的圆柱壳，结构最低模态频率对应于周向模态n=1时的梁式弯曲振动频率，壳体上任意点的切向位移v和径向位移w大小相等，且它们的幅值满足V=-W，则在某截面上的各质点位移大小相等，方向相同，相当于整个圆截面做刚体运动[3]，这恰恰与简单二维梁理论的假设是相符的。如果仅考虑水下大长径比圆柱壳受横向激励时的低频域声辐射问题，采取合适的等效方法，可以通过计算水下梁的声辐射来预报圆柱壳的声辐射特性。为了和水下圆柱壳解析程序比较，本文以简支边界条件为例，给出水下圆柱壳振动与声辐射的梁等效计算方法，并在后续的数值计算中加以验证。

2.1 水下梁辐射声功率求解

忽略简谐时间因子e-iωt，水下Euler-Bernoulli梁振动控制方程为：

其中：w x（）为结构位移响应，E为杨氏模量，I为梁截面惯性矩，S为梁截面积，ρb为梁结构密度，ρw为流体密度，M为单位长度的附加水质量，g x（）为激励力，ω为激励频率。令g x（）=0，得到频散方程：

如果梁为简支边界条件，可以求得模态频率：

其中：L为梁长。对于细长的二维梁结构，单位长度的附加水质量可近似等于单位体积排开的水质量[6]。如果考虑圆柱体结构，需要在此基础上进行三维系数修正，这时的附加水质量将随模态变化，可以表示为：

其中：Kn为三维流体修正系数，可以由文献[6]查表获得。将位移响应写出模态叠加的形式，考虑边界条件和模态的正交性，可得到水下梁的激励响应：

在计算梁结构的远场辐射声压时，可将梁结构延轴线方向截成若干长度单元d x，对每一长度单元可采用带障板的圆柱体辐射声压表达式[10]。如果单元分得足够小，并考虑不同单元在场点处的相移，整个声场由各单元的声辐射叠加而成。在球坐标系下，声场p：

其中：R，θ，φ为声场在球坐标系下的坐标参量，λ为流体中声波波长，k为声场波数，a为结构截面半径。远场结构辐射声功率可对平均声强积分[11]得到：

2.2 等效梁算法

如果采用简单梁模型近似计算圆柱壳受横向激励时的低频域辐射声功率，需要保证梁的弯曲振动模态与圆柱壳（n=1）对应。由于梁模型只考虑了一维的横向位移，忽略与其它方向位移间的耦合作用，使得其只能与圆柱壳第一阶梁式弯曲振动模态对应，高阶模态偏差将增大。此外，如果圆柱壳的周向的其它模态（n≠1）不可忽略，这时梁模型将不再适用。计算表明，对于大长径比（L/a＞20）圆柱壳，水下圆柱壳低频声辐射特性主要决定于圆柱壳梁式振动模态（n=1）。为此，本文首先通过计算等效杨氏模量系数，使梁的弯曲振动模态与圆柱壳（n=1）在空气中的低频域内一一对应，再将圆柱壳的附加水质量引入到梁模型中近似流固耦合作用，进而利用这些等效后的弯曲模态采用模态叠加的方法，则可用简单梁模型等效计算水下圆柱壳声辐射特性。也可以说，对于大长径比（L/a＞20）圆柱壳，考查其受横向激励时的低频声辐射特性，可以将其简化成梁模型等效计算。

为表述方便，用上标“b”表示梁的相关参数，用上标“c”表示圆柱壳的相关参数，上划线“-”表示等效后的相关参数，其它符号和2.1节表示的相同。简支梁在空气中的模态频率为：

要利用（9）式等效计算圆柱壳的模态频率ωcn，对于梁模型，如果保持与圆柱壳相同的截面半径、截面积等结构参数，则二者截面惯性矩相等，并令密度也相同，即：

若将圆柱壳固有弯曲振动频率ωc写成等效梁参数的表达形式，选取合适的杨氏模量系数，总能获

n得与圆柱壳对应等效的各阶弯曲振动模态：

其中：Cn为第n阶等效杨氏模量系数，E为材料实际的杨氏模量。值得注意的是，这里的E¯n不仅使梁和圆柱壳的模态频率相同，还使它们的模态振型相同。为了得到Cn的具体解，需要首先获得空气中圆柱壳固有梁式（弯曲）振动模态ωcn（对于简支边界可以通过解析方法计算得出，对于其它边界则需要通过数值方法计算得出）。通过后续分析可知，Cn主要与圆柱壳的长径比有关，对于相同长径比、不同长度、不同厚度的薄壳Cn值相同，因此只要计算出其中一种结构参数下的ωcn便可得到Cn，并且在后续的计算中不需重复计算。如果附加水质量的作用只影响结构的线密度，则用等效梁方法得到的水下圆柱壳弯曲模态频率：

如果激励为在x=x0位置的谐和点力，记为G x0（），则可得到水下等效圆柱壳受迫振动的位移响应：

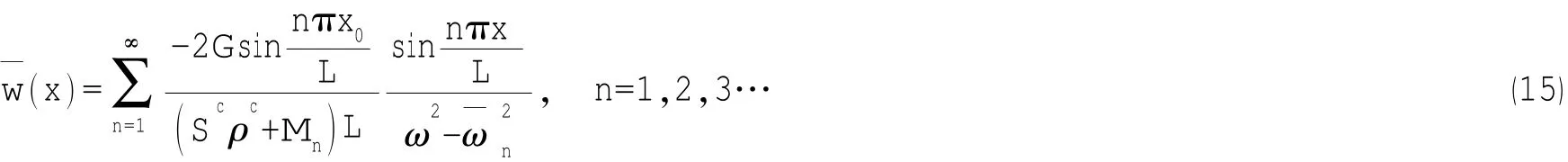
根据第2.1节方法，可以计算得到水下等效圆柱壳的辐射声功率。

实际上本文的等效方法是利用了水下大长径比圆柱壳低频声辐射特性主要决定于圆柱壳梁式振动模态的特性，将等效获得的水下圆柱壳梁式弯曲振动模态应用到了简单梁模型中，将水下圆柱壳低频振动与声辐射的三维问题简化为一维问题处理，大大提高了计算效率。若利用附加水质量近似流固耦合作用，并将其加到空气中的圆柱壳振动方程中去，求解位移系数矩阵行列式，计算出水下壳体的模态频率，再进一步求解振动方程位移系数矩阵的逆得到壳体的受迫响应，相对传统的流固耦合计算也可得到相应的简化，但本文方法更为简便。如果与附加水质量三维修正系数一样，将Cn作为先验知识绘制成图表供计算查询，利用（14）、（15）式进行等效计算，则可避免反复计算圆柱壳位移系数矩阵及矩阵求逆带来的计算困难。

3 数值计算

3.1 圆柱壳低频声辐射特性分析

首先分析水下大长径比（L/a＞20）圆柱壳受到横向激励时，梁式振动模态（n=1）对低频域声辐射的作用。水下圆柱壳振动的控制方程采用近似薄壳振动理论Donnell方程描述。假设圆柱壳简支在无限长圆柱障板上，利用壳位移的模态叠加形式解，将振动控制方程在模态空间分解，并根据模态正交性和边界条件，进行空间傅立叶变换分析，可求得声场声压和声阻抗[12]。壳体的辐射声功率可以由表面声强的表面积分得到：

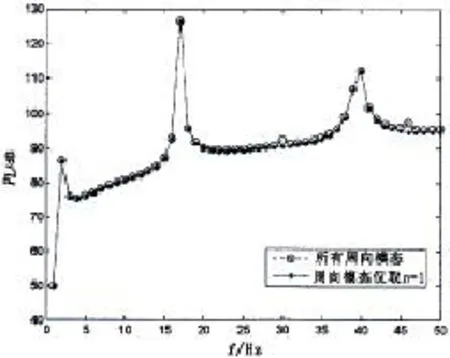
数值计算圆柱壳的辐射声功率，分析梁式弯曲振动模态（n=1）对辐射声功率的影响。首先计算一个实例，圆柱壳结构参数为L=40m，a=1.75m，h=0.015m，E= 2.06×1011Pa，两端简支边界条件，在1/2L位置施加一个单位点力。满足数值计算收敛性，如果圆周方向只取梁式弯曲振动模态（n=1），分析圆柱壳梁式弯曲振动模态对辐射声功率影响，如图1所示，图中纵轴PL表示辐射声功率级，参考声功率为0.67×10-18W，横轴f表示频率范围。计算出的声功率在低频域与取所有周向模态计算出的基本相同。如果以图1中声功率低频域前三个峰值频率激励的结构计算位移响应，则对应于第1、3、5阶梁式弯曲振动模态结构振型。可以看出，水下圆柱壳低频声辐射特性主要决定于圆柱壳梁式振动模态。

进一步计算表明，大长径比（L/a＞20）的水下圆柱壳受横向激励时，梁式弯曲振动模态（n=1）对圆柱壳低频辐射声功率的贡献远大于其它周向模态，前五阶弯曲频率范围内的辐射声功率能量集中在n=1的周向模态贡献上，因此仅用梁式弯曲振动模态等效计算水下圆柱壳低频辐射声功率是可行的。由于圆柱壳的最低模态频率对应于周向模态n=1时的梁式弯曲振动频率，因此仅选取n=1的周向模态计算圆柱壳的辐射声功率，第一阶弯曲振动频率以前的计算结果是准确的。而本文分析中没有考虑阻尼对各阶模态的作用，在前五阶弯曲振动频率范围内仅选取n=1的周向模态计算圆柱壳的辐射声功率，可能漏掉因达到其它低阶周向模态共振带来的峰值，但由于这些共振模态对圆柱壳低频辐射声功率的贡献远小于梁式弯曲振动模态，因此，此时的计算结果（n=1）与取所有周向模态的计算结果变化规律一致。

3.2 等效梁方法验证

为了验证本文等效梁算法的准确性，这里通过比较圆柱壳和等效梁的水下模态频率、激励响应和辐射声功率的吻合程度来校验。以图1所取圆柱壳参数和激励方式为例，采用2.2节等效梁方法计算该圆柱壳结构的辐射声功率并与3.1节计算结果比较，验证方法的有效性。

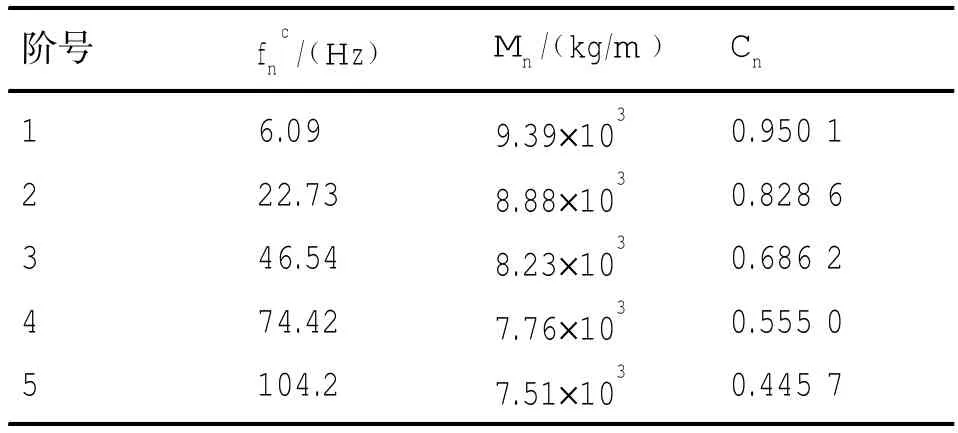
表1 圆柱壳的等效梁计算参数Tab.1 Calculating parameters of equivalent beam for cylindrical shell

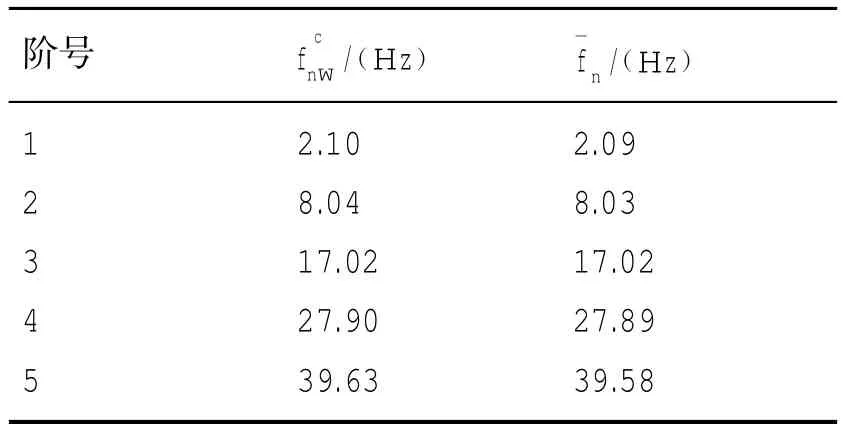
表2 水下圆柱壳前五阶固有弯曲振动频率Tab.2 The first five natural bending frequencies of underwater cylindrical shell

等效参数列于表1，其中fnc通过解析方法[1]计算得出，Mn由（4）式得到，Cn由（13）式计算得到。利用表1参数并按照2.2节等效梁算法计算得到的水下圆柱壳弯曲振动频率与解析法计算结果比较列于表2，二者计算的频率吻合很好。进一步比较用等效梁方法计算水下圆柱壳的振动响应，圆柱壳1/2L处有单位点力激励，激励点处的位移响应比较如图2所示。

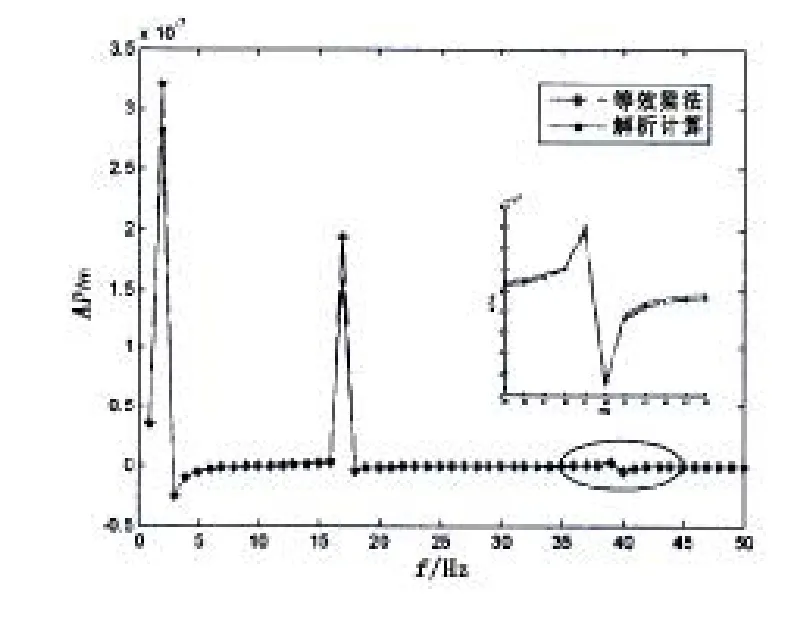
图2 激励位置处的结构位移响应图Fig.2 Displacement responses of the driving point

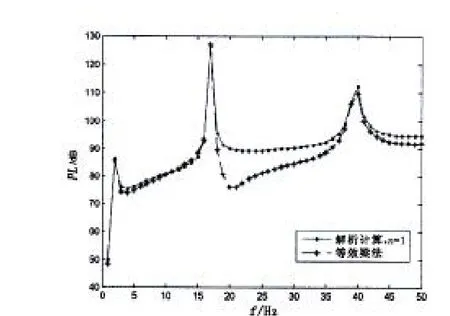
3辐射声功率的解析法与等效梁法比较Fig.3 Comparison of radiated sound power levels between analytic solution and equivalentbeam method

图2 中纵轴AP表示响应幅度，横轴f表示频率范围。结构将发生共振的条件是，激励频率等于模态频率且激励位置位于模态的非节点位置。而此时激励位置相对结构长度方向对称，则仅在第1、3、5阶模态频率附近激励时，结构发生共振，其它激励响应相对共振峰值很小。等效计算结果和解析法计算结果比较，二者吻合很好，验证了本文等效算法计算水下圆柱壳受迫响应的准确性。

分别用解析法和等效梁方法计算水下圆柱壳的辐射声功率，计算结果如图3示。可以看出，两曲线变化规律一致。由于等效梁模型只考虑横向位移，而忽略了与其它方向位移间的耦合作用，也忽略了其它方向振动响应对辐射声功率的贡献，使等效梁计算结果与解析计算结果间存在偏差，但计算结果中最为关心的辐射声功率峰值频率和对应幅度可以很好地吻合。本例验证了用等效梁方法计算水下圆柱壳辐射声功率的有效性。

4 等效梁算法分析

分析水下大长径比圆柱壳的低频声辐射特性，给定圆柱壳结构参数及边界条件，可以通过等效杨氏模量系数，将其模拟为等效梁计算振动及声辐射。研究发现，在满足薄壳假设下，各阶等效杨氏模量系数主要与圆柱壳的长径比有关，在满足径厚比20＜a/h＜100时，可以忽略厚度的影响，下面来证明这一结论。

等效杨氏模量系数由（13）式给出，将圆柱壳结构视为细长圆管，此时截面积Sc和截面转动惯量Ic表示为[13]：

其中：h为圆柱壳厚，则（13）式可以表示为：

由文献[3]计算得出，对于长径比L/a＞20的简支薄壳，只要周向弯曲半波长和轴向弯曲半波长均远大于壳体厚度，半径与厚度比（a/h）在满足20＜a/h＜100时，不同径厚比对弯曲振动模态（n=1）影响不大，即上式中圆柱壳弯曲振动频率变化主要与L和a有关。实际上对上述结论中径厚比的条件约束可以进一步的放宽，对于3.1节实例中的a/h=116.7同样适用，在下面的计算例中加以验证。如果h相对a是小量，按照文献[3]的计算假设，忽略h对ωcn的影响，从（18）式可计算得出h对Cn的影响将小于0.1‰。如果L=40m，a=1.75m，分析厚度变化对结构前五阶弯曲模态频率的影响，列于表3，可以看出，厚度变化对圆柱壳低阶弯曲振动模态频率影响不大。

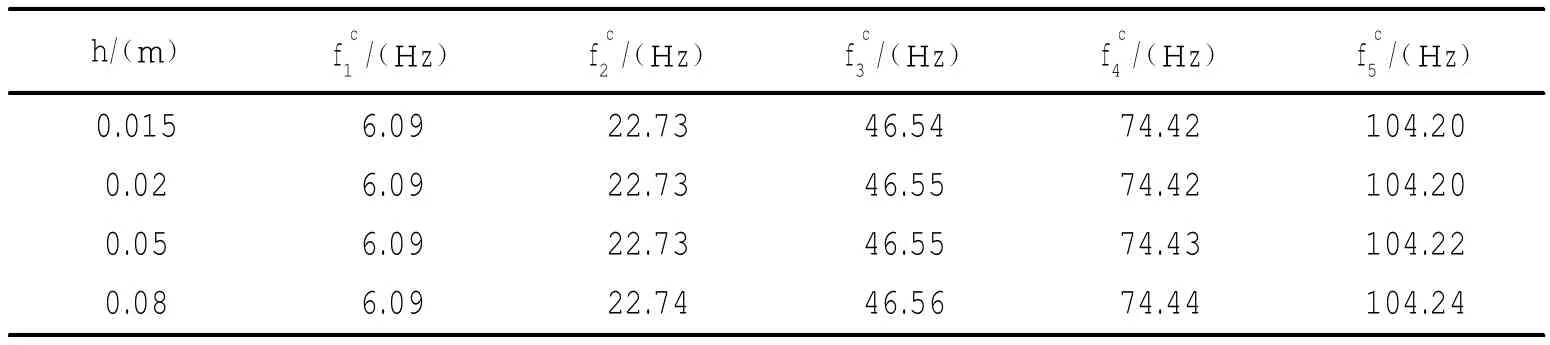
表3 厚度变化对圆柱壳弯曲模态频率影响Tab.3 Effect of variant thickness on the natural bending frequencies of cylindrical shells

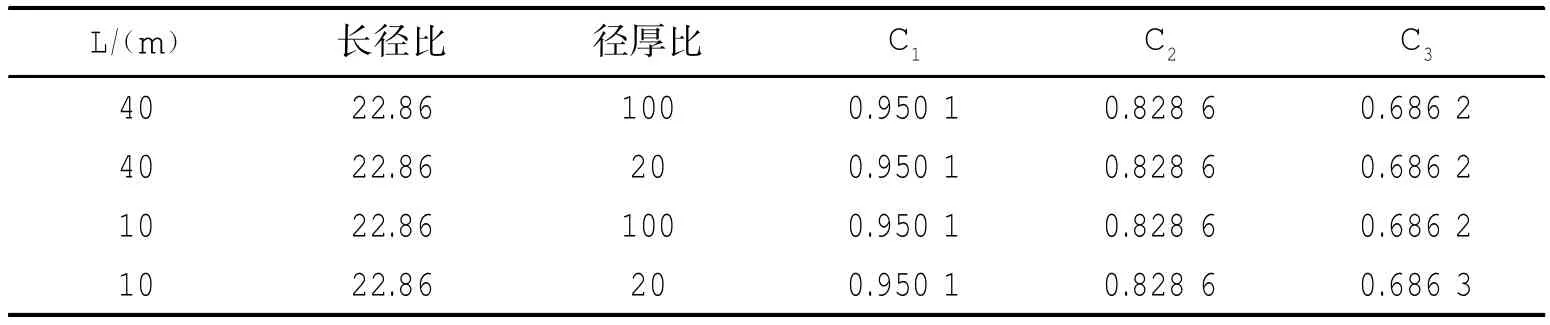
表4 长度和厚度对等效杨氏模量系数的影响Tab.4 Effect of different thickness on the natural bending frequencies of cylindrical shells

以长径比为22.86的圆柱壳为例，分析长度和厚度对前三阶等效杨氏模量系数Cn的影响，列于表4，可以看出，各阶等效杨氏模量系数只与圆柱壳的长径比有关。为方便计算，给出不同长径比圆柱壳前五阶等效杨氏模量系数曲线，如图4所示。利用梁模型并结合图4曲线，可准确预报圆柱壳低频域辐射声功率及梁式弯曲振动的模态。

为了验证本文方法及图4给出的等效杨氏模量系数曲线的实用性，仅改变3.1节算例厚度参量，h= 0.03m，其它结构参数不变，根据本节分析，此时厚度的变化不改变Cn的取值，令附加水质量Mn也与表1对应参数相同，重新计算水下圆柱壳弯曲振动频率及辐射声功率。等效梁计算结果和解析程序计算结果fnc

W比较列于表5，二者计算频率吻合很好，前五阶固有频率误差均小于1%。水下圆柱壳的辐射声功率计算结果的比较如图5示，两曲线变化规律一致，尤其在前三阶弯曲振动频率范围内吻合极好。

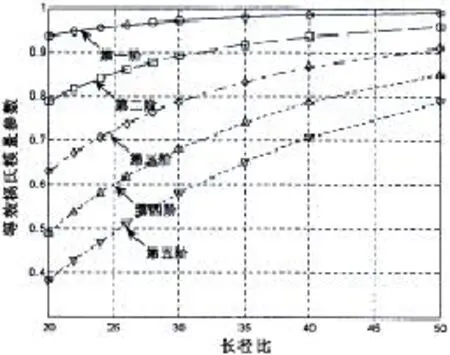
图4 等效杨氏模量系数曲线Fig.4 Coefficients of equivalent Young’s modulus curves

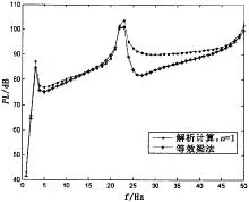
图5 等效梁法计算辐射声功率结果Fig.5 Results of radiated sound power levels are calculated by using equivalentbeam method

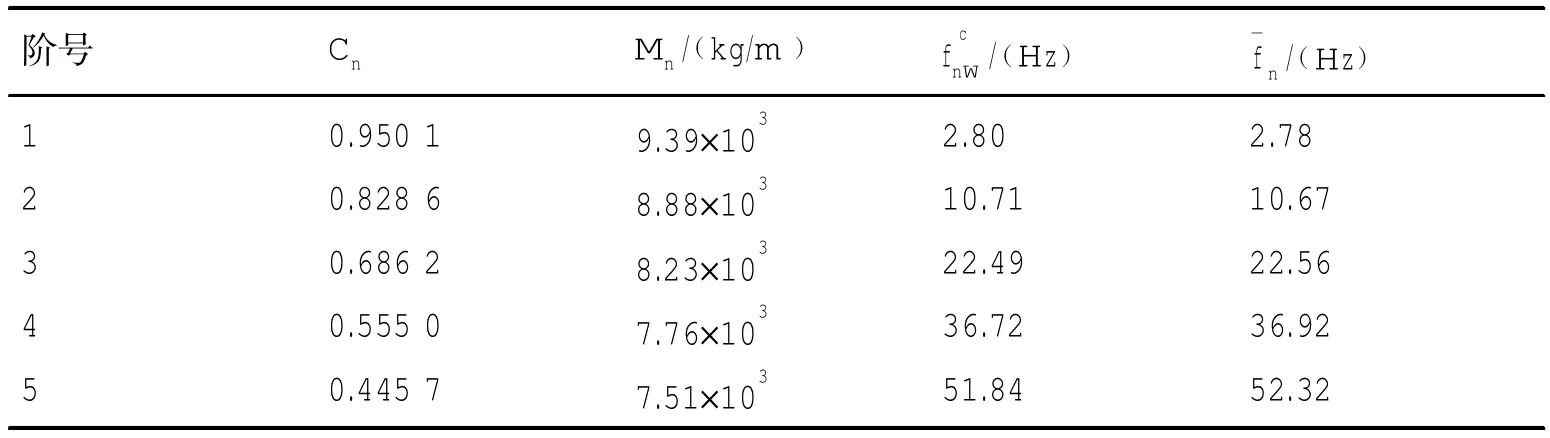
表5 等效梁参数及计算结果Tab.5 Parameters and solution results of equivalent beam

5 结论

（1）大长径比水下圆柱壳（L/a＞20）低频声辐射特性主要决定于圆柱壳梁式弯曲振动模态（n=1），可以利用水下等效梁算法提高圆柱壳低频振动响应和辐射声功率的计算效率。利用附加水质量近似结构与水的耦合作用，将结构振动和辐射声场分开计算，基于Euler-Bernoulli梁理论，推导出了水下梁弯曲振动响应表达式；利用带障板的圆柱体辐射声压表达式和远场声压叠加原理，给出了水下梁辐射声功率的表达式。

（2）给定圆柱壳结构参数及边界条件，可以通过等效杨氏模量系数，将其模拟为等效梁计算振动及声辐射。运用水下圆柱壳辐射声功率解析表达式和本文等效梁方法，比较分析了大长径比（L/a＞20）水下圆柱壳算例的低频声振特性，验证了本文方法的有效性。

（3）计算表明，等效杨氏模量系数只与圆柱壳的长径比有关，在半径与厚度比（a/h）在满足20＜a/h＜100范围内，可以忽略厚度对其的影响。给出了不同长径比圆柱壳前五阶模态频率的等效杨氏模量系数曲线，利用梁模型并结合此曲线，可准确、快速预报圆柱壳低频域辐射声功率及梁式弯曲振动模态，为高效分析加肋及有横舱壁的大长径比复杂圆柱壳的低频声辐射特性提供了可借鉴的方法。

[1]何祚镛.结构振动与声辐射[M].哈尔滨:哈尔滨工程大学出版社,2001:110-124. He Zuoyong.The vibration and the sound radiation of structures[M].Harbin:Harbin Engineering University Press,2001: 110-124.

[2]Tang rui,Liqi,Shang dejiang.A method for predicting the vibrations of underwater cylindrical shells by using the equivalentbeam model[J].J.A.S.A.,2012,131(4):3507.

[3]Forsberg K.Axisymmetric and beam-type vibrations of thin cylindrical shells[J].AIAA Journal,1969,7(2):221-227.

[4]Sun JQ.Vibration and sound radiation of non-uniform beams[J].Journal of Sound and Vibration,1995,185(5):827-843.

[5]Wallace C E.Radiation resistance of a baffled beam[J].J.A.S.A.,1972,51(3):936-945.

[6]陆鑫森,金咸定,刘涌康.船体振动学[M].北京:国防工业出版社,1980:190-213. Lu Xinsen,Jin Xianding,Liu Yongkang.Ship vibration theory[M].Beijing:Industry of Defence Press,1980:190-213.

[7]Tang R,LiQ,Shang D J.Research on the forced vibration and sound radiation of an underwater non-uniform beam with arbitrary boundary[C]//Proceedings of the 5th International Symposium on Acoustic Engineering and Technology.Harbin: NLUAT,2010:100-104.

[8]Junger M C,Feit D.Sound,structures,and their interaction[M].2nd edition.Massachusetts:Cambridge Press,1985:206-209.

[9]Ho Shinghuei,Chen Chaokuang.Analysis of general elastically end restrained non-uniform beams using differential transform[J].Applied MathematicalModeling,1998,22:219-234.

[10]Junger M C.Sound radiation by resonances of free-free beams[J].J.A.S.A.,1972,52(1):332-334.

[11]Zheng H,CaiC.Minimization of sound radiation from baffled beams through optimization of partial constrained layer damping treatment[J].Applied Acoustics,2004,65:501-520.

[12]刘涛.水中复杂壳体的声-振特性研究[D].上海:上海交通大学,2002:15-38. Liu Tao.Research on sound and vibration characteristics of complex cylindrical shell submerged in water[D].Shanghai: Shanghai Jiaotong University,2002:15-38.

[13]何祚镛,赵玉芳.声学理论基础[M].北京:国防工业出版社,1981:174. He Zuoyong,Zhao Yufang.The base of acoustical theory[M].Beijing:Industry of Defence Press,1981:174.

An equivalentmethod for calculating the vibration and sound radiation of underwater cylindrical shells in the low-frequency range

TANG Rui,SHANG De-jiang,LIQi
(Acoustic Science and Technology Laboratory,Harbin Engineering University,Harbin 150001,China)

In order to improve the computational efficiency of the vibration and the sound radiation of underwater cylindrical shellswith large length-to-radius ratio in the low-frequency range,amethod by using the equivalent beams is proposed.The equivalent beam theoreticalmodel is based on Euler-Bernoulli beam theory,in which the interaction between the structures and water is approximated to added mass.Different equivalent Young’smodulus coefficients for the beam models are obtained,through which themodal frequencies of the beams aremade identical to the beam-typemodal frequencies of the cylindrical shellwith large length-to-radius ratio(L/a＞20).The results show that the equivalent Young’smodulus coefficients are mainly dominated by the length-to-radius ratio for cylindrical shells,and the effect of the shell thickness on those ismuch weaker.The equivalent Young’smodulus coefficients curves for the first five order beamtype natural frequencies of cylindrical shellswith different length-to-radius ratio are calculated,through which the radiated sound power and the beam-typemodes of underwater cylindrical shells in the low-frequency range can be precisely predicted by using a simple beam theoreticalmodel.

cylindrical shell;vibration;sound radiation;Euler-Bernoullibeam;

TB532 TB561

A

10.3969/j.issn.1007-7294.2014.11.013

1007-7294（2014）11-1377-09

2014-02-26

国防973项目资助（613100）

唐锐（1981-），男，哈尔滨工程大学讲师，E-mail：tangrui@hrbeu.edu.cn；

商德江（1969-），男，哈尔滨工程大学教授，博士生导师，E-mail：shangdejiang@hrbeu.edu.cn。