基于INSGA-II的等效水深截断系泊系统优化设计
2014-06-12张火明陆萍蓝张晓菲中国计量学院浙江省流量计量技术研究重点实验室工程训练中心杭州310018
张火明,陆萍蓝,张晓菲(中国计量学院.浙江省流量计量技术研究重点实验室;.工程训练中心,杭州310018)
基于INSGA-II的等效水深截断系泊系统优化设计
张火明a,陆萍蓝b,张晓菲a
(中国计量学院a.浙江省流量计量技术研究重点实验室;b.工程训练中心,杭州310018)
深海平台混合模型试验的首要任务是等效水深截断系统的优化设计,其目的是以截断水深系统替代全水深系统进行试验。等效水深截断系统相比全水深系统其工作水深和跨度较小,但其它特性两者应保持一致。文章以工作在304 m水深的10万吨内转塔式系泊FPSO为例,截断水深为76 m,采用改进的非支配排序遗传算法(INSGA-II)对等效水深阶段系统进行了优化计算,同时考虑了总系泊系统水平和垂直两个方向以及具有代表性的单根系缆的静力特性。此实验数值结果表明,所采用的数学模型、优化方法是行之有效的。
深海平台;混合模型试验技术;等效水深截断;优化设计;FPSO
1 引言
随着海洋油气资源开发逐渐向深海转移,而涌现出来的新型深海平台主要有:张力腿式平台(TLP),立柱式平台(SPAR),半潜式平台(SEMI)和浮(船)式生产平台(FPSO)。在复杂海洋环境中,风、浪、流、冰载及平台上的机器和设备各种载荷的作用下,会引发深海平台强烈的振动。在此情况下,系泊系统的重要作用就不言而喻了,作为深海平台的重要组成部分,系泊系统为其提供了海上定位的能力,在加强深海平台安全的同时,也为油气开采的稳定进行提供了保证。因此,对深海平台及其系泊系统的研究迫在眉睫且意义重大。通常,可以采用物理模型试验和数值计算两种研究手段[1],由于数值计算常采用许多假设条件可能会导致结果不可靠,因此,海洋工程界普遍采用模型试验。然而海洋平台及其系泊系统由于较大的空间尺寸的特性,即使采用常规缩尺比(1/50-1/100)得到的模型仍然超过目前试验水池的尺度范围。物理模型试验和数值模拟方法都有各自的优缺点,就目前而言,综合两者优点而成的混合模型试验方法是最广泛使用且最被认可的深海平台模型试验方法。
进行混合模型试验方法最需要考虑解决的是设计符合全水深系统特性的等效水深截断系统,使其能够替代全水深系统在现有水池尺度下进行试验。理论上,等效水深截断系统的工作水深和跨距会比全水深系泊系统小一些,但是其他的特性应该尽量保持一致[2]。因此,如何设计出尽可能与全水深系统的特性保持一致的等效水深截断系统,就涉及到优化算法的思想。而等效水深截断系统优化设计属于多目标优化问题[3],则将选取一个多目标优化算法来进行分析求解。
非支配排序遗传算法(non-dominated sorting genetic algorithm,NSGA)是由Srinivas和Kalyanmoy[4]于1995年提出的,它首次将非支配排序的概念引入了多目标优化领域,并取得了较好的效果。但是NSGA本身存在许多不足之处,主要在于:1)计算复杂性较高;2)缺乏精英策略;3)需要特别指定共享半径。这使得它在处理高维、多模态等问题时,难以得到满意的结果。因此,Kalyanmoy等人[5]提出了NSGA-II解决上述问题。NSGA-II发展至今,已广泛运用于多个领域。李琳等人[6]基于NSGA-II提出新的算法,对石油钻机的钻速、寿命等钻进参数进行了多目标的优化,通过统计证明了模型和算法是满足要求的;Safarzadeh和Motahhari[7]通过NSGA-II对一油井的生产方案进行了优化,在减少风险的同时还提高了开采率;Mashael等人[8]提出了基于超启发式算法的学习选择方法解决多目标优化问题,该方法结合了NSGA-II、SPEA2和MOGA三种算法,此外还将该方法应用于车辆耐撞性的设计问题中,并通过对比其它方法证明了该法的有效性。
然而NSGA-II算法仍存在一些不足之处,本文作者在文献[9]中对NSGA-II做了改进。在NSGAII的基础上,修改了精英策略,此外,使用模拟二进制交叉算子和非均匀分布变异算子,更好地维持了种群的多样性。采用改进的非支配排序遗传算法(INSGA-II)优化截断水深系统与全水深系统静力特性相似程度,可提高搜索范围以及提高解的精度。
2 改进的非支配排序遗传算法(INSGA-II)
将父代与子代合并,并且从二倍种群数量中选取出最好解以保证优良种群,这是NSGA-II算法中的精英策略,但这种方法的问题是容易陷入局部最优解。在此基础上,本文提出了改进的精英策略,以此避免算法中出现的早熟的问题。第一步是需要获得第一级的非支配个体(pareto解),这里对二倍种群进行快速的非支配排序,然后适当地“遗弃”个体,不再将所有pareto解填充到下一代种群中,采取将每一级的非支配个体集“遗弃”一个体的策略,然后经过多级排序及填充后,会有一小部分的精英个体被遗弃。这样不仅可以保证绝大多数的精英个体能留在下一代种群中,而且也避免了全部精英参与到下一代中,从而防止种群提前收敛或陷入局部最优解。此外,重新设计了遗传算子,采用非均匀变异算子和模拟二进制交叉算子进行了多次试验,使算法在性能上更加稳定,也平衡了进化前期的广泛搜索和进化后期的集中搜索,从而种群的多样性得到维护、保持。
改进的非支配排序遗传算法(INSGA-II)步骤如下:
(1)随机初始化种群,大小为N;
(2)对初始种群进行非支配排序,并进行选择,交叉,变异,然后完成初始种群的合并;
(3)将合并后的种群的拥挤度进行计算,并进行快速非支配排序;
(4)选取新父种群:选取第一级的非支配个体集F1,遗弃个体后进行新父种群重新填充,接着再对后面的集合进行选取。当选取到F1时,转(5)。如果新父种群中的个体个数超过N,则优先填充拥挤度较大的个体;
(5)对新父种群进行选择,交叉,变异操作,判断进化代数满足终止条件,若满足,则退出算法并输出结果,否则转(6);
(6)将子代与父代进行合并,转到(3),流程图如图1所示。
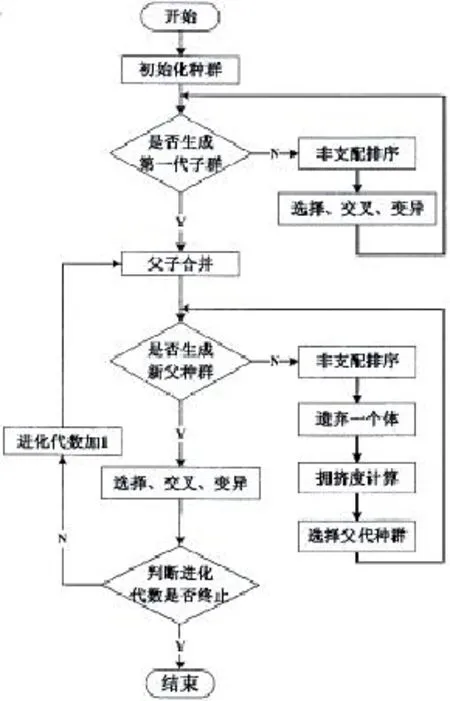
图1 算法流程图Fig.1 Flow chart of INSGA-II
3 等效水深截断系统数学模型
等效水深截断系统优化设计的目的,就是要尽可能地使得深海平台在截断水深获得和实际全水深一致的运动响应[10],因此,必须遵循相应的等效设计原则。目前,国际上公认的等效设计原则[11]主要有:
(1)保证锚泊线的数目及其布置情况与立管一致。
(2)保证系泊系统对平台的静回复力与立管一致。
(3)保证平台在准静定耦合条件下得到的系泊系统静力特性与立管一致。
(4)保证单根系缆的张力特性与立管一致。
(5)保证系缆在波浪和海流中的流体动力与立管一致。
上述原则可以确保等效水深截断系统与全水深系统的特性相似,但要使静力和动力特性完全等效,基本上是不可能的。就目前的进展来看,第一条容易得到满足,静力部分可以近似地满足,而动力等效的原则就比较困难了。
本文主要考虑截断水深系泊系统和全水深系泊系统两种情况下静力特性相似,那么首先应分别求出两种情况下的静力特性。这两种系统的静力特性计算过程是类似的。
3.1 锚泊系统静力特性计算
综前所述,首先计算锚泊系统的静力特性,其中包括总系泊系统及单根锚泊线的张力—位移特性。目前研究中,对系泊系统静力分析的方法有很多[12-13],本文根据文献[14]进行求解。
图2为锚泊总系统静力特性计算示意图。其计算过程为:选取水平移动距离d x(一般以系统初始静平衡时位置为0点,偏移距离依次取-2m、-4m、-6m、…、-50m,这里假设纵荡偏移的范围为-50~ 0m)的上端系缆点,计算每根锚泊线相应每个d x的新的水平跨距,再在相应的数组中通过插值计算求出锚泊线的上端点张力及水平和垂直张力。水平张力向X轴正方向投影,合成后得到上端系缆点移动后X方向的水平恢复力,垂直张力可直接合成得到Z方向的垂直恢复力。完成一系列d x计算后,可得到锚泊系统总的水平恢复力—水平偏移(Offset)曲线和锚泊系统总的垂直恢复力—水平偏移(Offset)曲线。3.2目标函数
等效水深截断系统优化设计最重要准则是使等效水深截断系统与全水深系统的特性尽可能保持一致,特性差值尽可能最小化。本文主要考虑单根代表性的锚泊线张力—位移特性,总系统水平恢复力—位移特性以及总系统垂直恢复力—位移特性一致性。
数值上可通过如下数学公式(1)表达:

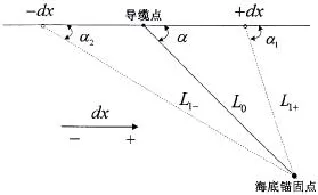
图2 锚泊总系统静力特性计算示意图Fig.2 Calculation of the overallmooring system’s static characteristic
其中:F1为总系统截断水深与全水深的水平恢复力—位移特性差值;Fhfull()i为全水深情况下总系统的水平恢复力—位移特性;Fhtrun()i为截断水深情况下总系统的水平恢复力—位移特性;F2为总系统截断水深与全水深的垂直恢复力—位移特性差值;Fvfull()i为全水深情况下总系统的垂直恢复力—位移特性;Fvtrun()i为截断水深情况下总系统的垂直恢复力—位移特性;F3为单根代表性锚泊线截断水深与全水深的张力—位移特性差值。Tfull()i为全水深情况下单根代表性的锚泊线张力—位移特性;Ttrun()i为截断水深情况下单根代表性的锚泊线张力—位移特性;np表示离散点个数。需要说明的是,由于表征静力特性的是一条曲线,因此,需要在曲线上取若干离散点进行计算。
在考虑静力特性相似的情况下,等效水深截断系统优化设计主要考虑锚泊线的分段长度、破断强度、轴向刚度、单位长度水中重量以及浮筒/重块水中重量。而破断强度和轴向刚度在指定材质和构造形式情况下,直径将对其起决定性作用。
4 数值试验
本文以一工作水深为304m的10万吨转塔式FPSO的系泊系统作为研究对象,选取的模型缩尺比λ为80,截断水深为76m。
4.1 系统描述
该FPSO采用内转塔式系统,由转塔、系泊系统、立管系统三部分组成。
如图3所示,此次模型试验中不模拟立管系统。其系泊系统总共由9根系泊缆组成,分为3组各3根。3组系泊缆均匀布置成120°,每组3根相邻的系泊缆成5°间隔均匀布置。
9根系泊缆属于同一类型,都是多成分系泊缆。每根系泊缆自上而下(即从与转塔连接处到与海底锚链连接处)分别由接转塔钢索、中间钢索和末端锚链这3段组成。具体参数见表1。每根系缆的预张力为300 kN。
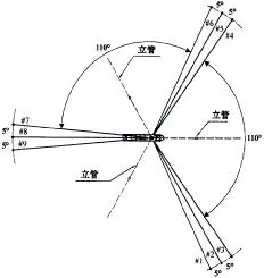
图3 转塔式系泊系统布置平面图Fig.3 Plan view of the turretmooring system

表1 304m水深系泊缆主要参数与属性(实际值)Tab.1 M ain parameters of themooring line of the 304m system,full scale
4.2 试验分析与结果
在模型试验过程中发现,将原系泊系统从与转塔连接处到与海底锚链连接处的中间钢索分为两段,在其间加上一个适当的重块,可以使得截断系统和原系统的特性也更加接近和吻合。因此,将变量调整如表2所示,其中给出了变量的范围。

表2 优化设计变量上下限取值范围Tab.2 Upper lim it and lower lim it of the optim ization variable

表3 INSGA-II算法参数Tab.3 Parameters of INSGA-II
针对上述系统,采用INSGA-II算法获取静力特性相似的截断水深系统。编制C++程序,在VC++6.0平台下编译通过,从得到的一组pareto优化解中,根据需要选择[0.037 224 9,0.042 679 9,0.017 820 4]。对应的最优点为[108,15.455 8,-287 084,158.8,41.478 7,376 805,177.5,32.620 8,33.434 5,315.693]。其三目标的pareto优化曲面如图4所示,其中,F1与F3的pareto优化曲线如图5所示;F2与F3的pareto优化曲线如图6所示。得到的截断系统的物理特性参数如下表4所示。

表4 最优点对应截断系统的锚泊线各材质分段物理特性参数Tab.4 M ain parameters of themooring line of the truncated system-76m at the optimum point
单根代表性的锚泊线张力—位移特性以及总系统水平恢复力位移特性和总系统垂直恢复力位移特性比较如图7、图8所示。锚泊线初始水下形状如图9所示。其中,L1-P表示全水深系统单根代表性锚泊线静力特性,L1-T表示截断水深系统单根代表性锚泊线静力特性。FH-P表示全水深系统总水平恢复力—位移特性,FH-T表示截断水深系统总水平恢复力—位移特性;FV-P表示全水深系统总垂直恢复力—位移特性,FV-T表示截断水深系统总垂直恢复力—位移特性。L1S-P表示全水深系统单根锚泊线初始水下形状,L1S-T表示截断水深系统单根锚泊线初始水下形状。
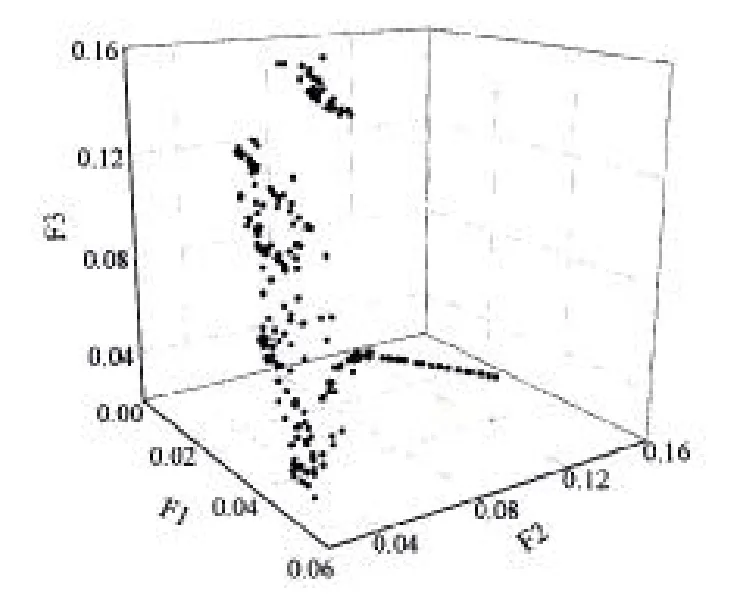
图4 三目标函数Pareto优化曲面Fig.4 Pareto optimization curve of three functions
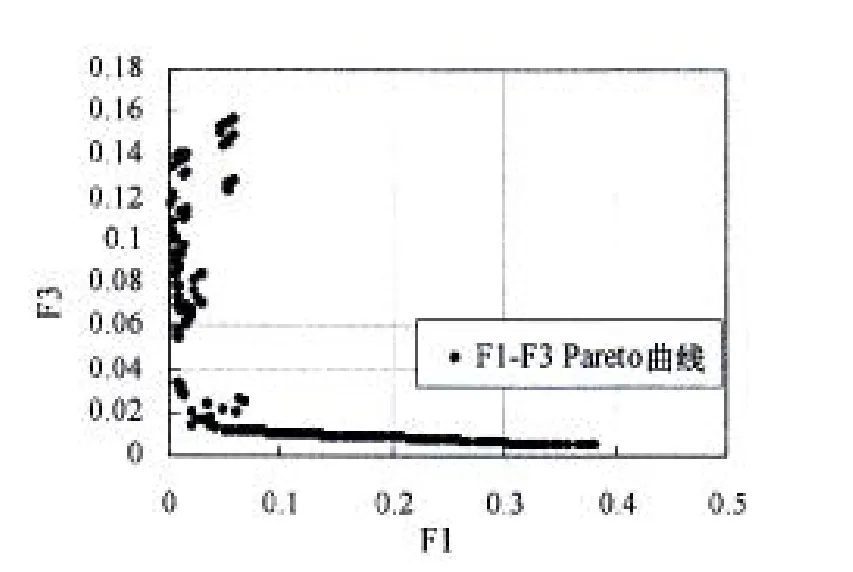
图5 F1与F3的Pareto优化曲线Fig.5 Pareto optimization curve of F1and F3
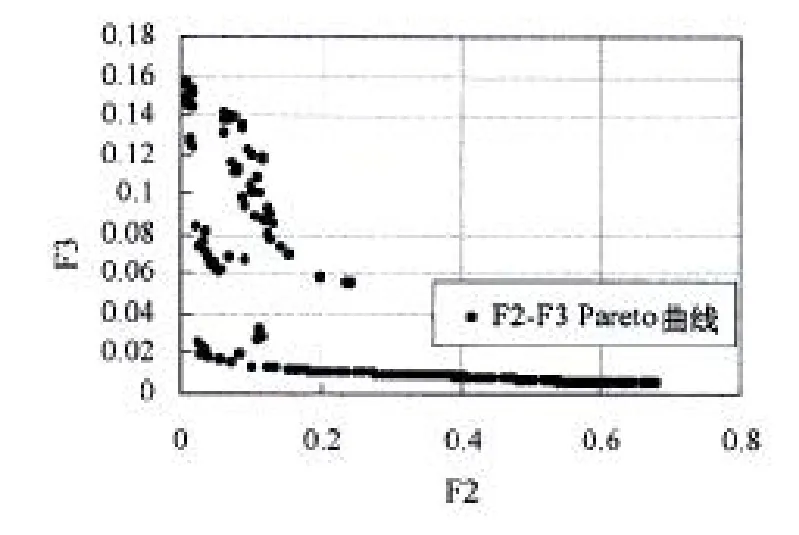
图6 F2与F3的Pareto优化曲线Fig.6 Pareto optimization curve F2and F3
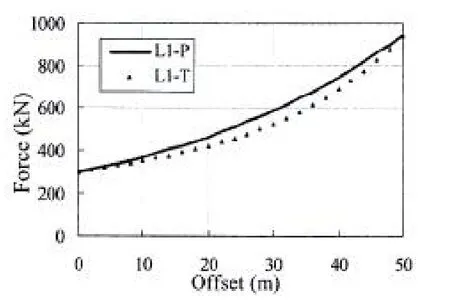
图7 单根锚泊线张力—位移特性比较Fig.7 Tension-offset curve of the simplemooring line of the truncated&full depthmooring system
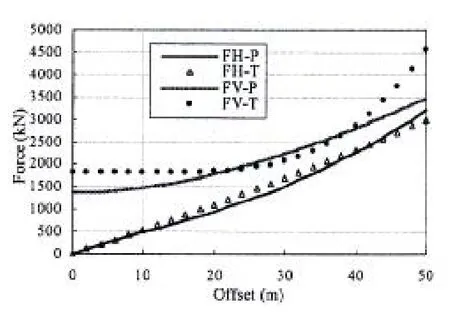
图8 总系统恢复力—位移特性比较Fig.8 Over restoring force-offset curve of the

图9 锚泊线初始水下形状Fig.9 Initiation underwater shapes of themooring line truncated&full depthmooring system
由上述图表可以得出结论:等效水深截断系统与全水深系统的静力特性近似一致。
5 结论
本文采用改进的非支配排序遗传算法(INSGA-II),并同时考虑对等效水深截断系统与全水深系统的总系泊系统水平和垂直两个方向以及具有代表性的单根系泊缆静力特性相似进行了优化。由于本文考虑到多个目标,改进的非支配排序遗传算法实现了多个目标间的平衡,从而更快更准地设计出等效水深截断系统来替代全水深系统进行模型试验,进而了解其水动力学性能,为设计出稳定可靠的浮式生产系统提供技术参数和科学依据,对海洋工程的研究和深海海洋油气资源的开发具有积极的意义。
[1]Zhang Huoming,Yang Jianmin,Xiao Longfei.Investigation on hybrid model testing technique of deep-sea platforms based on equivalentwater depth truncation[J].China Ocean Engineering,2007,21(3):401-416.
[2]苏一华,杨建民,肖龙飞.深海单柱式平台及其系泊系统的截断水深模型试验[J].上海交通大学学报,2007,41(9): 1454-1459,1464. Su Yihua,Yang Jianmin,Xiao Longfei.The experiment of a deepwater spar and itsmooring system at truncated water depth[J].Journal of Shanghai Jiaotong Unversity,2007,41(9):1454-1459,1464.
[3]苏一华,杨建民,肖龙飞,李欣.基于静力相似的水深截断系泊系统多目标优化设计[J].中国海洋平台,2008,23 (1):14-19. Su Yihua,Yang Jianmin,Xiao Longfei,Li Xin.Multi-objective optimization design of truncated mooring system based on equivalent static characteristics[J].China Offshore Platform,2008,23(1):14-19.
[4]Srinivas N,Kalyanmoy D.Multiobjective optimization using nondominated sorting in genetic algorithms[J].Evolutionary Computation,1994,2(3):221-248.
[5]Kalyanmoy D,Agrawal S,Pratab A,etal.A fast elitistnon-dominated sorting genetic algorithm formulti-objective optimization:NSGA-II.KanGAL Report200001[R].Indian Institute of Technology,Kanpur,India,2000.
[6]李琳,张栋栋,沙林秀等.基于粒子群算法的钻进参数多目标优化[J].现代电子技术,2014,37(10):24-27. Li Lin,Zhang Dongdong,Sha Linxiu,et al.PSO-based multi-objective optimization of drilling parameters[J].Modern Electronics Technique,2014,37(10):24-27.
[7]Safarzadeh M A,Motahhari SM.Co-optimization of carbon dioxide storage and enhanced oil recovery in oil reservoirs using amulti-objective genetic algorithm(NSGA-II)[J].Petroleum Science,2014,11(3):460-468.
[8]Mashael Maashi,EnderÖzcan,Graham Kendall.A multi-objective hyper-heuristic based on choice function[J].Expert Systemswith Applications,2014,41(9):4475-4493.
[9]张晓菲,张火明.精英策略的改进非支配遗传算法[J].中国计量学院学报,2010,21(1):52-58. Zhang Xiaofei,Zhang Huoming.Improved non-dominated sorting genetic algorithm based on the elitist strategy[J].Journal of China University ofMetrology,2010,21(1):52-58.
[10]Zhang Huoming,Sun Zhilin,Yang Jianmin,Gao Mingzheng.Investigation on optimization design of equivalentwater depth truncatedmooring system[J].Science in China Series G.,2009,52(2):277-292.
[11]杨建民,肖龙飞,盛振邦.海洋工程水动力学试验研究[M].上海:上海交通大学出版社,2008:127-128. Yang Jianmin,Xiao Longfei,Sheng Zhenbang.Study on hydrodynamic ocean engineering[M].Shanghai:Shanghai Jiaotong University Press,2008:127-128.
[12]缪国平.挠性部件力学导论[M].上海:上海交通大学出版社,1996:40-46. Liao Guoping.Introduction of flexiblemechanical components[M].Shanghai:Shanghai Jiaotong University Press,1996: 40-46.
[13]潘斌,高捷,陈小红,陈家鼎.浮标系泊系统静力计算[J].重庆交通学院学报,1997,16(1):68-73. Pan Bin,Gao Jie,Chen Xiaohong,Chen Jiading.Static calculation of buoymooring fast[J].Journal of Chongqing Jiaotong Institute,1997,16(1):68-73.
[14]张火明,范菊,杨建民.复杂系泊系统静力特性快速计算方法研究[J].舰船科学技术,2007,29(3):113-118. Zhang Huoming,Fan Ju,Yang Jianmin.Investigation on quick computationmethod of the static characteristics of complex mooring system[J].Ship Science and Technology,2007,29(3):113-118.
Investigation on optim ization design of equivalent water depth truncated mooring system based on INSGA-II
ZHANG Huo-minga,LU Ping-lanb,ZHANG Xiao-feia
(a.Zhejiang Provincial Key Laboratory of Flow Measurement Technology;b.Engineering Training Center, China Jiliang University,Hangzhou 310018,China)
The primary task of deep-sea platform hybrid model test is to optimize the design of equivalent water depth truncated system.Its purpose is to truncate the system to replace the full depth one to carry out the test.Compared with the full-depth system,work depth of the equivalent depth truncation system ismore shallow and span is smaller,but other characteristics of both should be consistent.In this paper,a 100 thousand tons,turretmoored FPSO working in the 304m water depth is taken for example,its truncated depth is 76 m,using an improved non-dominated Sorting Genetic Algorithm(INSGA-II)to the equivalent depth system optimal calculation.And the horizontal and vertical direction’s restoring characteristic of total mooring system as well as the static characteristics of a representative singlemooring line are taken also into account.The numerical results of this experiment show that themathematicalmodel and optimal algorithm used are effective.
deep sea platforms;hybridmodel testing technique;equivalentwater depth truncation;optimization design;FPSO
U661.1
A
10.3969/j.issn.1007-7294.2014.11.003
1007-7294(2014)11-1292-07
2014-09-26
浙江省青年科学家培养计划项目(2013R60G7160040);浙江省自然科学基金资助项目(Y14E090034);国家自然科学青年基金资助项目(51379198)
张火明(1976-),男,中国计量学院副教授,E-mail:zhm102018@163.com;陆萍蓝(1976-),女,工程师,E-mail:dylpl@163.com。
