新课标下立体几何教学的分析与探讨

底军艳

摘 要：新课标改革对高中数学教学提出了新的要求，在此背景下，作为培养学生逻辑推理能力、空间想象能力、几何直观能力的载体，立体几何在高中数学教学中显得至关重要。如何提高立体几何课堂教学的效果，通过怎样的手段实现教学效率最大化成为了新课标改革中备受关注的问题。本文中，笔者就对立体几何教学的现状、教学目标以及方法策略进行分析和探讨。

关键词：新课标 立体几何教学 现状分析 策略探讨

中图分类号：G633.6 文献标识码：A 文章编号：1673-9795（2014）02（c）-0056-01

作为高中数学课程中唯一一门对学生空间想象能力进行培养的课程，立体几何在新课程改革中是作为重点和热点内容被看待的。根据新课标对高中数学改革的内容来看，立体几何的教育功能主要可以从知识方面、数学能力方面以及情感态度方面进行分析。第一个知识方面，能够帮助学生掌握基本的关于立体图形的性质及概念；第二个数学能力方面，能够实现对学生几何直观能力、空间想象能力以及逻辑推理能力的形成和提升；第三个情感态度价值观方面，可以帮助学生提升对客观规律的思维能力。由此可见，在新课标改革下对立体几何教学的价值进行分析和探讨是具有重要意义的，是需要被广大教育者关注的一个重要问题。

1 立体几何研究现状

高中教学大纲中的立体几何知识具有抽象程度高、空间性强等特点，学生的积极性和容易受到打击，就算生硬地学完，过了一段时间往往也会几乎忘光。到了高三复习的时候，很多学生都有上新课这样的感觉，造成这种现象的根本原因就是学生缺乏系统的立体空间概念，逻辑推理论证能力没有得到锻炼。造成这一现象的因素有很多，第一，学生缺乏对数学语言的深入全面理解，空间想象力不够好。第二，老师在实际课堂教学中往往认为只要教会学生解题的方法就行了，对学生数学语言的培养不够重视。第三，关于教材内容编排方面，针对提高学生数学语言能力方面涉及地较少，也缺乏足够的练习。对我们的立体几何教学中存在问题进行分析后，我们就需要针对存在的问题进行改进，探讨更合理、科学的立体几何教学策略[1]。

2 新课标立体几何教学要求

2.1 重视直观感知，构建相关概念

在立体几何中，定理是指经过严格逻辑论证后的命题，并且我们需要承认只有通过直觉理解，学生才能真正想通领悟并接受。众所周知，创新往往发端于直觉，立体几何作为一种形象、直观的数学模型，其对提高学生创新精神、发展学生直觉能力上具有不可低估的价值[2]。学生在立体几何学习过程中，通过观察、操作、作图、设计、猜想等方式进行几何图形性质研究的过程中，往往能得到视觉和心理上的愉悦。这样就给学生提供了学习积极性，进而增强他们的探究好奇心，从而激发出潜在的创造力，最终就成为了我们所追求的创新意识。

2.2 注重培养学生抽象概括能力

在数学学习及知识理解中，直观固然重要，但直观只是一种手段，并不是目的。进行几何教育的目的不应该仅仅只是给学生灌输相关的图形理论知识，而更应该注重在过程中对学生各方面能力的培养，例如引导学生通过实物模型学会怎样将自然语言转化为符号语言和数字语言，又例如通过教导他们垂直关系、平行关系，让他们学会使用数学语言表达几何对象的位置关系。在这样的基础上，当学生的感性认识得到一定的积累后，就需要在适当的实际引导他们独立进行抽象概括、数学语言描述以及动手画图等活动。

3 立体几何教学策略研究

3.1 创设操作性问题情境

新课标教学要求强调，要重视教学过程中的问题情境创设，即帮助学生经历立体几何定理的形成过程中，加深他们对立体几何知识的理解、增强情感体验进而培养其空间想象力。在教学过程中创设动手操作问题，不仅能够激发学生的好奇心和学习兴趣，更能激发学生的联想思维，大大降低学生在学习过程中的排斥感和恐惧感。

例如，在进行凸多面知识点的教学中，教师们可以引导学生去发现周围生活中的各种多面体，而不是像传统教学一样，拿着各种几何体的模型在讲台上展示给大家看[2]。教师可以将学生进行合理分组，然后为每小组提供一個正方体框架，这些正方体的六个面对角线是用橡皮筋连接的，然后启发学生通过拉动皮筋构造出各种其他的多面体。这样现实的问题情境，能够让学生真正参与到学习中来，身临其中去感受和经历概念以及公式的形成、发展过程，进而加深他们对知识的理解和记忆。

3.2 培养学生灵活解题的能力

一般来说在解题中如果遇到向量坐标运算思维量较少、运算技巧较低等情况时，教师可以指导学生采用更便捷的解题方法，如建立合适的坐标系，并准确写出相关点的坐标。

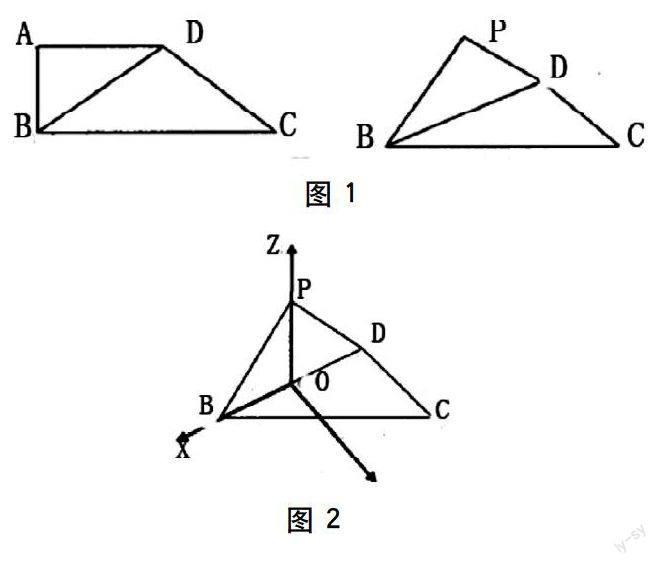
例如，如图1，已知四边形ABCD中，AD//BC，AD=AB=1，∠BCD=45°，∠BAD：90°，将△ABD沿BD折到如图1PBD的位置，使面PBD垂直于面BCD。（1）求证CD垂直于PB。（2）求二面角P—BC—D的余弦。（3）求点D到平面PBC的距离。

在上题中，由于图形中缺乏显性的空间直角坐标系的模型，我们可以利用综合法对线面位置关系进行分析，建立空间直角坐标系实现灵活解题，如图2，以BD中点O作为原点建立空间直角坐标系。

3.3 培养学生几何直观能力

一般我们所说的几何直观能力包括以下几点，分别为直观洞察能力、空间想象力以及图形语言思考问题的能力。受制于传统的几何教学常规作图工具，所有的图形都是静态的，学习过程时冷冰、死板的。针对这一问题，我们可以借助于现代信息技术，通过逼真而具体的动态演示将静态、抽象的图像展示给学生，帮助他们建立丰富的感性知识，进而发现立体几何问题的本质，达到教学的根本目的。

例如，在对定理：“三棱锥的体积等于它的底面积S与高h的乘积的三分之一”进行教学时，我们可以利用《几何画板》帮助学生进行探究学习，为学生提供动态的画面，诱发学生的联想能力，进而实现对他们类比能力的培养和提高。

参考文献

[1] 王小红.高中数学实验教学创设的几种途径[J].中学数学教学参考，2011（9）：23-25.

[2] 赵艳霞.新课标下立体几何教学初探[J].课改前沿，2010（5）：64-66.