注蒸汽井筒沿程热物性参数及热损失新算法

顾 浩， 程林松， 黄世军

（中国石油大学（北京）石油工程教育部重点实验室，北京 102249）

注蒸汽井筒沿程热物性参数及热损失新算法

顾 浩， 程林松， 黄世军

（中国石油大学（北京）石油工程教育部重点实验室，北京 102249）

基于干度的定义，对传统蒸汽干度方程进行改进，计算井筒热损失速率时，既按深度分段又按注汽时间分段，并采用Hasan等提出的两相流漂移流动模型计算井筒压力降.结果表明：改进后的模型用新算法的计算结果与现场实测值吻合很好，比传统的Beggs-Brill算法更准确.另外，在相同井深处，随着注汽时间的延长，蒸汽压力、温度和干度几乎不变，但是热损失速率逐渐降低.新算法为准确计算井筒热损失提供了参考.

热物性参数；热损失；压力降；算法

0 引言

在稠油热采注蒸汽阶段，准确计算井筒沿程热物性参数（压力、温度和干度）以及热损失是评价注汽效果的关键，对提高蒸汽的热利用率具有重要指导意义.目前，国内外开展了大量研究［1－2］，但是仍存在不少问题.Ramey［3］首先建立了沿程温度分布和井筒传热模型，但是当注汽时间小于7d时，无因次地层导热时间函数不适用；Chiu等［4］对地层导热时间函数进行了改进，但是在计算沿程压力降时仍采用传统的Beggs-Brill算法，而该算法以及流动型态划分的标准是基于空气－水两相，并且在计算任意角度倾斜管的持液率时，都是在水平管的基础上乘以倾斜校正系数，用于蒸汽－水两相垂直管流，误差较大；陈月明［5］在建立沿程干度方程时，忽略了摩擦力做功；师耀利等［6］在计算注过热蒸汽井筒热损失时，虽然对井筒深度进行了分段，但是忽略了按注汽时间分段计算，事实上，向井筒注蒸汽过程中，径向热损失以及水泥环外缘温度既随深度变化，又随时间变化，因此，在计算时应对时间和深度都进行分段处理.

本文首先根据能量守恒、质量守恒以及传热学理论建立井筒沿程蒸汽压力、温度、干度和热损失模型.建立蒸汽干度方程时，抛弃传统的复杂方法［5，7－8］，而是从干度的定义出发直接求解，这种处理方法有两大优点：①使沿程干度计算更准确；②加快了整个模型的求解速度，因为传统算法对压力和干度都进行迭代，这里只需对压力迭代，而干度是在压力求解后直接按定义计算.其次，在计算沿程压力分布时，舍弃传统的Beggs-Brill和Orkiszewski等算法，采用Hasan等［9－10］提出的适合于蒸汽－水两相且垂直向下流动的漂移流动模型.最后，除了分深度段外还分时间段计算井筒热损失，使热损失的计算结果更准确，利用现场测试数据验证了改进后的模型及新算法的可靠性，并简要分析注汽时间对蒸汽压力、温度、干度和井筒热损失速率的影响.

1 数学模型

基本假设：①井口注入参数（蒸汽的质量流速、压力和干度）保持不变；②井底使用封隔器，保证蒸汽不窜入油套环空，油套环空充以低压空气；③油管中心到水泥环外缘的热量传递为一维稳定传热，而水泥环外缘到地层的热量传递为一维不稳定传热，不考虑沿井深方向的传热；④井内油管、隔热层和套管结构如图1所示.

1.1 沿程压力方程

在建立沿程压力方程时，文［11－12］忽略了蒸汽－水流动的方向性，对于向上的两相管流，克服重力增加压降，而在注蒸汽过程中，汽水两相向下流动，重力作用减小压降，根据能量守恒推导出压力平衡方程为

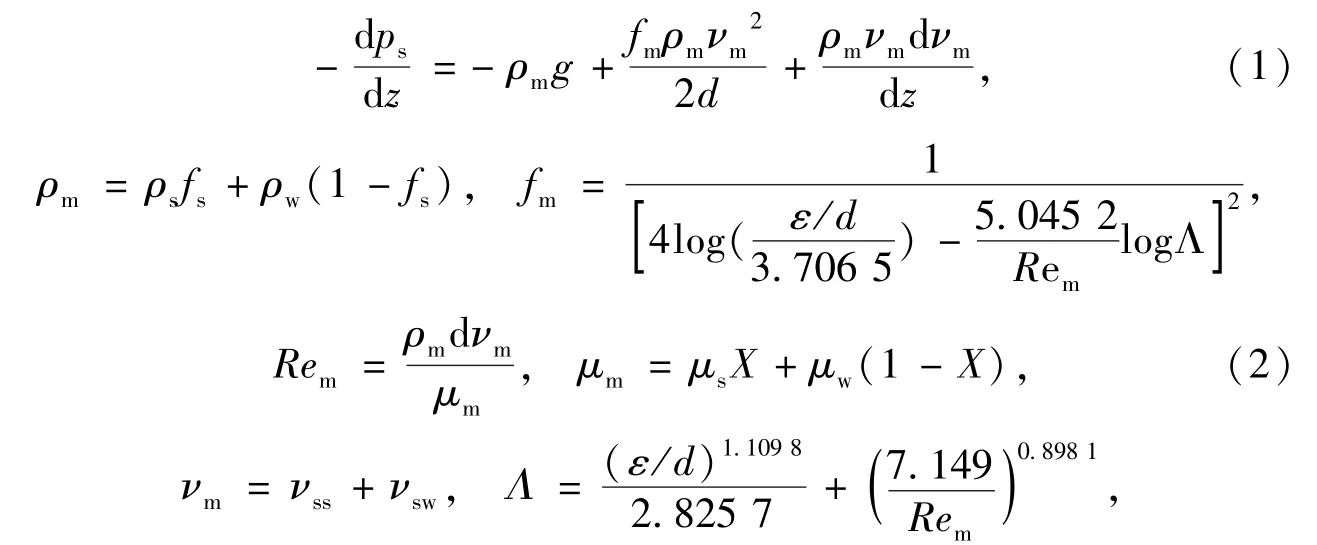
式中，ps为蒸汽的压力；－d ps为蒸汽压力降；z为井筒深度；ρs、ρw和ρm分别为蒸汽、水和混合物的密度；g为重力加速度；fm为两相流动的摩擦阻力因子；νm和Rem分别为混合物的流速和雷诺数；d为内管内径；fs为蒸汽体积分数；ε为内管粗糙度；Λ为无因次参数；μs、μw和μm分别为蒸汽、水和混合物的粘度；X为蒸汽的干度；νss和νsw分别为蒸汽和水的表观流速.

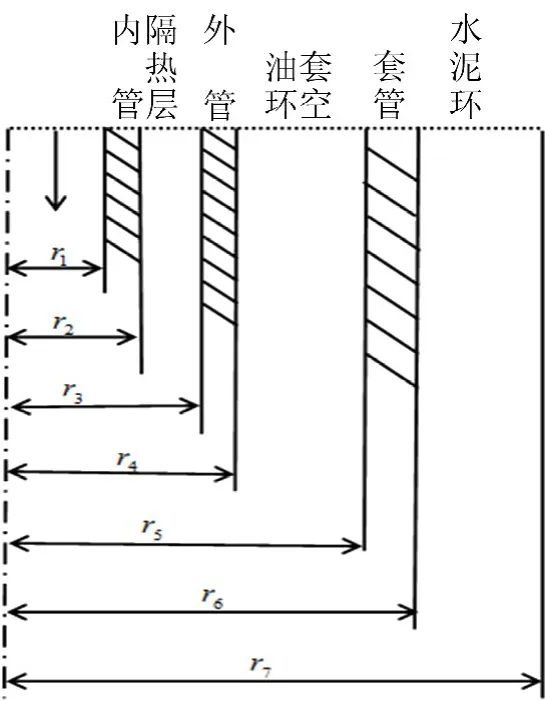
图1 井筒结构示意图Fig.1 Diagram ofwellbore structure

1.2 沿程温度方程

饱和蒸汽的温度和压力之间存在以下对应关系

式中，Ts为蒸汽的温度.

1.3 沿程干度方程

在计算沿程干度分布时，传统的方法［5，7－8］比较复杂：先求出热量损失和摩擦力做功，然后根据能量守恒计算饱和蒸汽的焓，最后通过辅助方程求出蒸汽的干度.这里从干度的定义出发，直接得到沿程干度方程为

1.4 井筒传热方程

当井口注汽条件不随时间变化时，井筒传热分为两部分：

1）油管中心到水泥环外缘的一维稳定传热.根据Fourier定律，得到稳定传热公式为

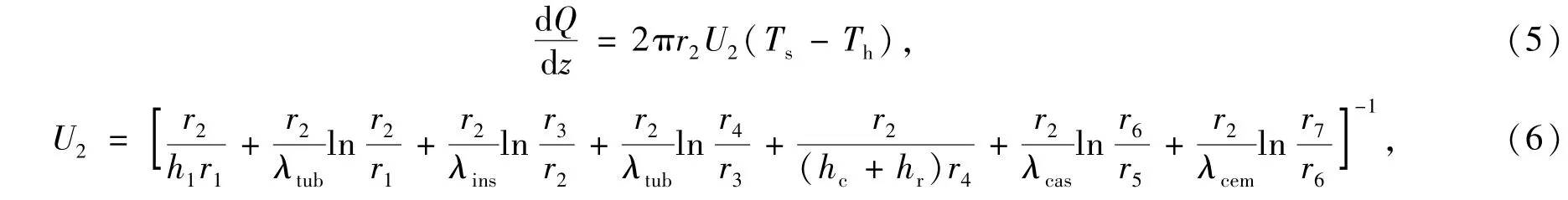
式中，d Q为单位时间内传递的热量；Th为水泥环外缘温度；U2为总传热系数；r1、r2、r3、r4、r5、r6和 r7分别为内管内径、内管外径、外管内径、外管外径、套管内径、套管外径和水泥环外缘半径；h1、hc和 hr分别为液膜污垢层对流、环空内自然对流和辐射换热系数；λtub、λins、λcas和 λcem分别为油管、隔热层、套管和水泥环的导热系数.

在方程（6）中，由于液膜污垢层对流换热系数（h1）和油套管导热系数（λtub和λcas）很大，对总传热系数U2的影响可以忽略不计，因此，（6）式可以化简为

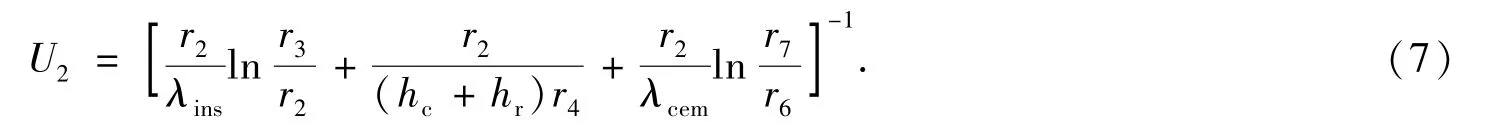
2）水泥环外缘到地层的不稳定传热.在注蒸汽过程中，水泥环外缘温度和地层温度随时间、深度变化，单位深度上的热损失速率可由下式表示［5］

式中，λe为地层导热系数；Te为地层温度；f（t）为地层导热时间函数，其准确表达式为［13］

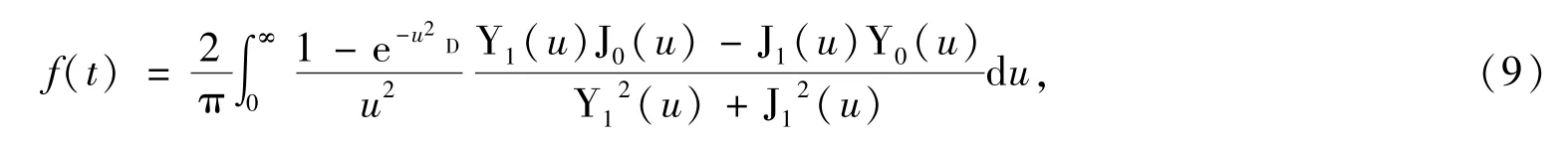
式中，D是无因次时间D＝αt／rh2，α是地层平均热扩散系数；u为拉式空间变量；Y0和Y1分别为第二类零阶和第二类一阶贝塞尔函数；J0和J1分别为第一类零阶和第一类一阶贝塞尔函数.

从（9）式可以看出：f（t）与D之间存在一一对应关系，如果采用解析法计算f（t）将十分复杂，一般采用半解析方法，即先通过解析法得到少量的数据点（D，f（t）），然后用较简单的函数关系式进行回归.目前，Ramey［3］、Chiu［4］和Hasan［13］分别提出了经典的回归公式，其表达式分别为

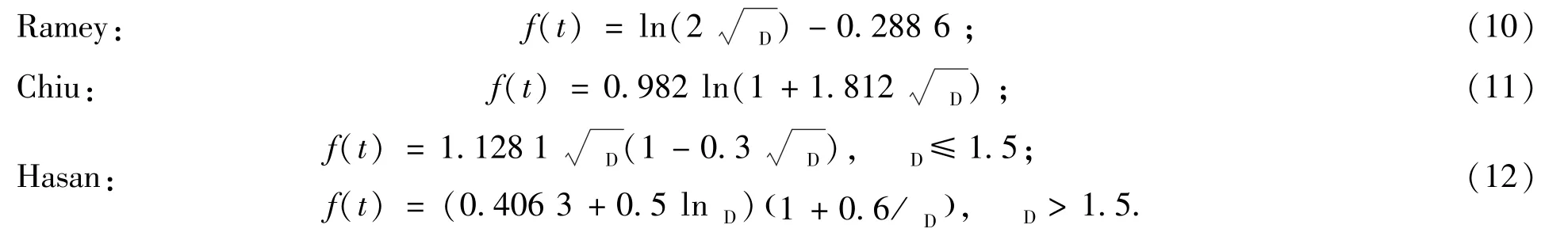
为了选择合适的回归公式，这里对比了上述三种经验公式与解析解之间的差异，如图2所示.从图2可以看出：当D≥10时，利用不同经验公式计算的地层导热时间函数值与解析解十分接近，但是当D＜5时，不同经验公式的计算结果存在一定的差别.Ramey公式与实际值差别最大，一般认为Ramey式适用于注汽时间超过7d［3］；Hasan公式误差最小，通过计算发现其最大相对误差仅为5.69%，但是，该公式在D＝1.5时不连续；Chiu公式误差略低于Hasan公式，但是由于精度能满足工程计算要求，因次，这里选择Chiu公式.

联立（5）式和（8）式，得到水泥环外缘温度为

图2 不同导热时间函数对比Fig.2 Heat-conduction time functions

由（5）式可知：要想求得单位深度上的热损失速率d Q／d z，必须先求得水泥环外缘温度Th和总传热系数U2，而（13）式表明Th与U2有关，因此，需要采取迭代法求解，这里采用文［14］中的经典算法求解总传热系数U2．

1.5 质量守恒方程

在整个注汽过程中，饱和蒸汽的质量流速保持不变

式中，is为饱和蒸汽质量流速.

2 模型计算方法及流程图

这里采用Hasan等［10］提出的两相流漂移流动模型计算井筒压力降，该模型充分考虑到流体的类型及流动方向，主要包括：蒸汽－水向下流动、气－油和气－水向上流动（同向）以及气－油逆向流动.对于注蒸汽过程，利用该模型求解井筒压力降的关键是针对蒸汽－水两相且垂直向下的管流确定蒸汽的体积分数fs，其原理如下.

向井筒注湿蒸汽的过程中，汽水两相向下流动，蒸汽受到向上的浮力，其速度为［10］

式中，νs为蒸汽相对于地面的流速；C0为流动参数；ν∞为气泡上升速度.

由（16）式可知：为了计算fs，关键是要求出C0和ν∞，而C0和ν∞又与流动型态以及不同流型下的流动规律有关.Hasan等将流型划分为泡流、分散泡流、段塞流、混状流和环流，并确定了每种流型的边界条件以及C0和ν∞的计算方法，具体参考文［10］.

另外，在计算井筒热损失速率时，传统算法忽略了对注汽时间分段，事实上，井筒热损失速率是井筒深度和注汽时间的函数，因此，严格的算法应该是得到某一时间段内某一深度段的热损失快慢.改进后的算法，其计算流程如图3所示.

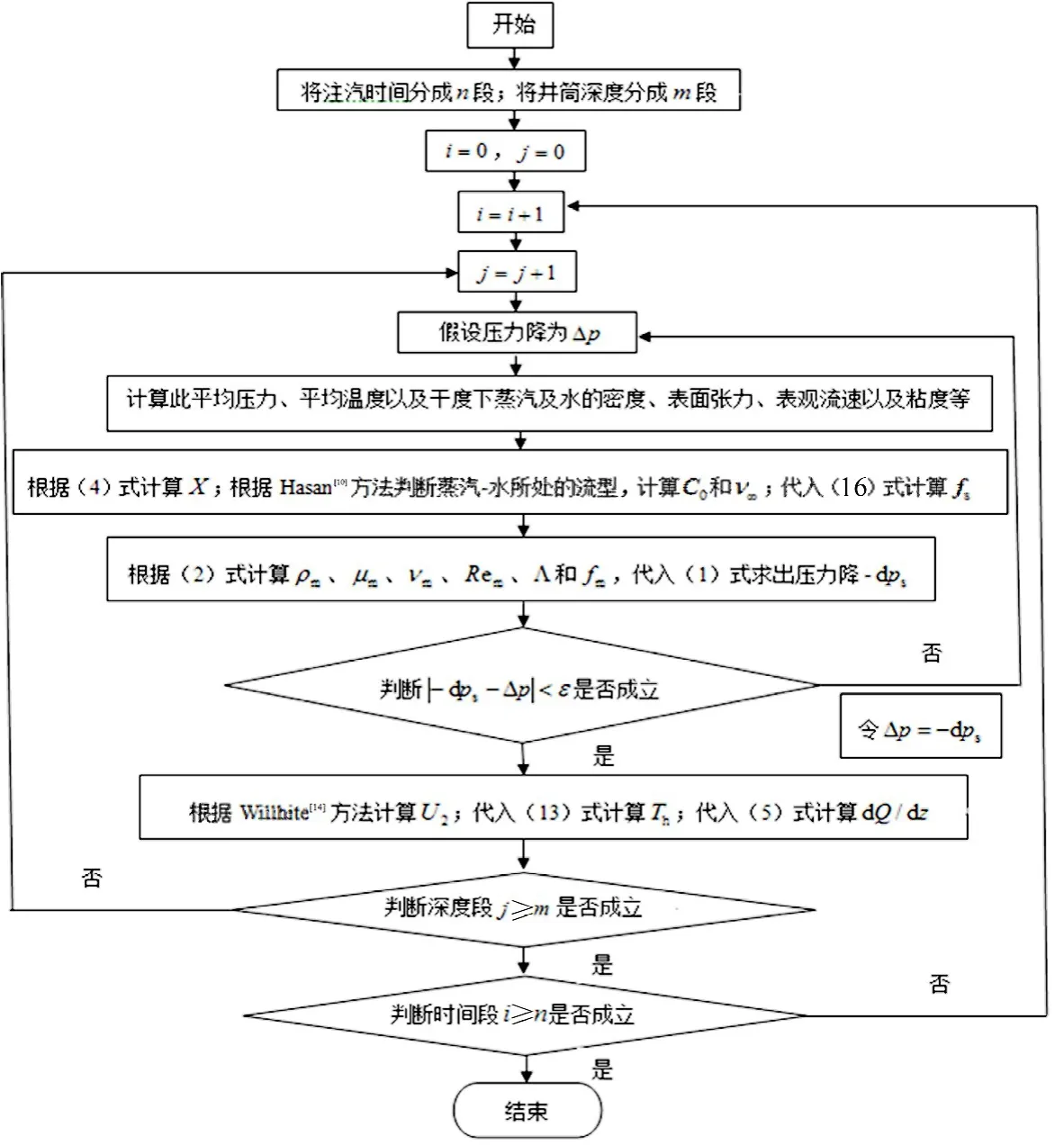
图3 计算流程图Fig.3 Flowchart for solution

3 算例与分析

3.1 模型验证

为了验证上述模型的准确性及算法的可行性，以某低渗稠油区块某吞吐井为例，将新算法得到的蒸汽压力、干度与现场实测值以及Beggs-Brill方法的计算值对比，如图4和图5所示，其中，注汽速度5 t·h－1，注汽时间10 d，表1为基础计算数据.从图4和图5可以看出：新算法得到的蒸汽压力和干度与实测值十分接近，而传统的Beggs-Brill方法得到的压力值与实测值存在较大偏差且干度计算值略高于实测值.另外，这里还计算了辽河油田齐40块5口注汽井的井底蒸汽压力和干度的测试值与新算法计算值之间的相对误差，如表2所示.

3.2 注汽时间的影响

表3为井深1 000 m处，不同注汽时刻井筒热物性参数及热损失的计算结果.可以看出：蒸汽压力、温度和干度在相同井深处几乎不随时间变化，但是单位深度上的热损失速率随着注汽时间的增加逐渐减小.这是因为在注汽初期，水泥环外缘温度较低，蒸汽与水泥环外缘温差较大，由（5）式可知，热损失速率大；随着注汽时间的延长，水泥环外缘温度逐渐升高，温差减小，导致热损失速率变慢.因此，在计算井筒热损失速率时，严格的算法应该是既要按井筒深度分段也要按注汽时间分段，即热损失速率表征的是某一注汽时刻某一井深处的热损失快慢.

图4 蒸汽压力计算结果Fig.4 Steam pressure

图5 蒸汽干度计算结果Fig.5 Steam quality

表1 基础计算数据Table 1 Basic calculation data

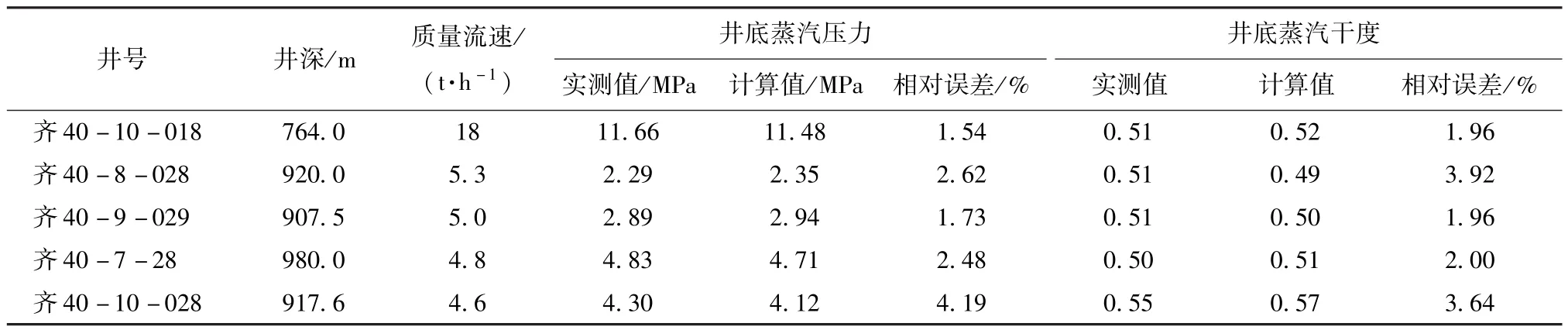
表2 辽河油田齐40块注汽井井底蒸汽压力和干度的测试值与计算值误差分析Table 2 Error analysis for bottomhole steam pressure and quality of fault Qi40，Liaohe oilfield

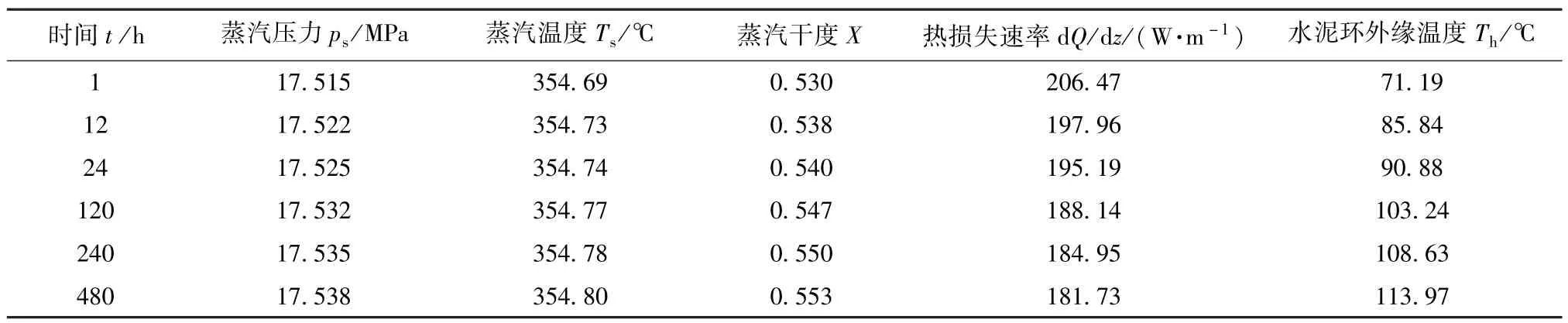
表3 注汽时间的影响Table 3 Effect of injection time

4 结论

1）在建立沿程干度方程时，从干度定义出发，与传统复杂方法相比，该方法不仅使沿程干度计算更准确，而且大大减少了迭代次数和计算量.

2）在求解热损失速率时，既要对井筒深度分段，也要对注汽时间分段，通过现场实测数据验证了改进后的模型及新算法的可靠性.

3）在相同井深处，随着注汽时间的延长，蒸汽压力、温度和干度几乎不变，但是热损失速率逐渐降低.

［1］Li Zhaomin，Zhang Dingyong，Yi Huaifeng，etal.Flow and heat transfer regulation ofmulti-thermal fluids injetion in wellbore［J］.Journal of China University of Petroleum，2012，36（6）：79－83.

［2］Bahonar M，Azaiez J，Chen Z.A semi-unsteady-state wellbore steam／water flow model for prediction of sandface conditions in steam injeciton wells［J］.Journal of Candian Petroleum Technology，2010：49（9）：13－21.

［3］Ramey H J.Wellbore heat transmission［J］.Journal of Petroleum Technology，1962，14（4）：427－435.

［4］Chiu K，Thakur SC.Modeling ofwellbore heat losses in directionalwells under changing injection conditions［R］.SPE 22870，Society of Petroleum Engineering，1991：517－528.

［5］Chen Yueming.Thermal recovery by steam injection［M］.Dongying：University of Petrolum Press，1996：64－83.

［6］Shi Yaoli，Du Dianfa，Liu Qingmei，etal.A calculationmodel forwellbore heat loss and pressure drop considering steam phase state changing in superheated steam injetion well［J］.Xinjing Petroleum Geology，2012，33（6）：723－726.

［7］Ni Xuefeng，Cheng Linsong，Li Chunlan，et al.A new model for the steam properties in steam injection wells［J］.Chinese Journal of Computational Physics，2005，22（3）：251－255.

［8］Xu Anzhu，Mu Longxin，Fan Zifei，et al.New fingdings on heatloss of superheated steam transmitted along the wellbore and heating enhancement in heavy oil reservoirs［C］∥IPTC 16439，IPTC Programme Committee，2013：1－10.

［9］Hasan，A R.Void fraction in bubbly and slug flow in downward vertical and inclined systems［J］.SPE Production＆Facilities，1995，10（3）：172－176.

［10］Hasan A R，Kabir C S，Sayarpour M.A basic approach to wellbore two-phase flow modeling［R］∥SPE 109868，Society of Petroleum Engineering，2007：1－9.

［11］Yang Dewei，Huang Shanbo，Ma Donglan，etal.Selection ofmodels for two-phase flow in the steam injection well［J］.Journal of University of Petroleum，1999，23（2）：44－46.

［12］Li Xiaoping，Wang Dawei，Lin Jie，et al.Calculation of wellbore steam parameters in heavy oil thermal recovery wells［J］. Xinjiang Oil＆Gas，2011，7（1）：68－71.

［13］Hasan A R，Kabir C S.Heat transfer during two-phase flow in wellbores：PartⅠ-formation temperature［R］∥SPE22866，The Society of Petroleum Engineering，1991：469－477.

［14］Willhite G Paul.Over-all heat transfer coefficients in steam and hot water injection wells［J］.Journal of Petroleum Technology，1967，14（4）：607－615.

New Algorithm for Thermophysical Parameters and Heat Loss along Wellbore During Steam Injection

GU Hao，CHENG Linsong，HUANG Shijun
（Key Laboratory for Petroleum Engineering of the Ministry ofEducation，China University of Petroleum，Beijing 102249，China）

Traditional equation of steam quality is improved based on definition.Rate of wellbore heat loss is calculated with both depth step and time step.Drift-fluxmodel of two-phase flow by Hasan is used to estimate pressure drop in wellbore.It indicates that results ofmodified model and new algorithm agree well with field date.They aremore accurate than Beggs-Brillmethod.In addition，steam pressure，temperature and quality are almost unchanged at the same depth.However，rate of wellbore heat loss decreases with injection time.The algorithm provides a reference for accurate calculation ofwellbore heat loss.

thermophysical parameters；heat loss；pressure drop；algorithm

date：2013－08－02；Revised date：2013－12－10

TE345

A

1001-246X（2014）04-0449-06

2013－08－02；

2013－12－10

国家科技重大专项（2011ZX05012-004，2011ZX05024-005-006）和辽河油田科技项目（特超深层高存水油藏提高蒸汽热利用率技术研究）联合资助

顾浩（1989－），男，硕士，博士生，主要从事热力采油技术、油气渗流理论和油藏数值模拟研究，E-mail：guhao110110＠163.com