一种气体低温吸附模型与计算

薛社生， 李守先， 刘 阳

（北京应用物理与计算数学研究所，北京 100094）

一种气体低温吸附模型与计算

薛社生， 李守先， 刘 阳

（北京应用物理与计算数学研究所，北京 100094）

研究化学氧碘激光器中工作气体氧的低温吸附.考察气体流过沸石多孔床的压力与速度的关系，建立吸附剂吸收的物质量与气流中物质量关系的吸附平衡方程.由吸附物量较少的特点，得出在确定的压力梯度下速度近似为常数.吸附平衡方程与吸附速率方程，构成低温吸附模型方程，其中，亨利等温线方程作为辅助关系.对模型方程做数值求解，得到气流中单态氧浓度及吸收的单态氧浓度随时间变化的规律，及浓度分布的长时间渐近特征.

吸附；多孔介质；化学氧碘激光；数值计算

0 引言

通过吸附作用过滤杂质或有害气体，是一项常见且很有实用价值的技术，其最早应用源于防毒面具的制造［1］.目前，用活性碳或硅胶作吸附剂吸附气体，已在化学工业中得到普遍应用，相关的研究工作仍在开展［2］.

化学氧碘激光器（COIL）的研究一直受到较多的关注［3－4］.高效率小型化是研究与设计的追求目标，采用吸附技术，将通过光腔的工作物质吸收然后解吸，封闭循环再利用，是减小系统体积、降低成本、提高工作效率的有效途径.具体地说，COIL装置中氧气、氯气及碘蒸气的含量较少，而稀释气体氦气（氖气）含量较大，设法将氧气等通过低温吸附去除，而把氦气（氖气）通过封闭循环再利用，显然既有利于废气排放，又可以降低成本.因而，沸石分子筛低温吸附技术受到COIL工作者越来越多的关注.

计算吸附过程就是要确定吸附剂的需要量、被吸附气体的量、吸附过程的持续时间、吸附器的尺寸以及能量的消耗.通过光腔后的气流处于较低的压力状态，吸附过程是混合气体在较低压力下，流过多孔材料时进行的.本文从COIL工作物质流过吸附床层的速度与压力的关系出发，结合吸附动力学关系，建立吸附模型，并对相应的模型方程做数值求解，给出吸附过程氧浓度变化的规律.

1 床层吸附物理模型

气体通过沸石分子筛床层被吸附的过程简示于图1.当气体从左端进入床层，一部分被孔隙表面吸附，另一部分从右端流出.由于吸附的可选择性，可以将气体部分吸收.

图1 气体分子筛床层吸附示意图Fig.1 Schematic of zeolite adsorption bed

COIL工作气体中氦气含量较大，氧气含量较少，混合气体通过光腔后处于较低压力状态（压力一般为几个毫米汞柱高）.先考察气体的流动速度与压力之间的关系.

1.1 混合气体流动模型

设通过光腔的氦气／氧气混合气体沿一通道进入沸石吸附床，由于沸石具有吸附选择性，可以只将其中的氧气吸收去除.一般地，氦／氧的摩尔比约为4∶1，氧的含量相对较少，吸附就变成了去除混合气体中少量组分的过程.另外，氧气的低温吸附热较低，释放的热量并不显著，完全可由稀释气体带走.所以，吸附过程可看作在等温状态下进行，且由吸附引起的混合气体的压力降也较小.把在较低的压力和温度下穿过多孔材料的气体，作为理想气体处理，并略去材料的形变，于是，气体运动是一遵循达西定律的渗流过程.渗流速度方程［5］

其中v，p，μ，K分别为流体速度，压力，粘性系数及渗透率.低密度（低压力）下的气体渗透，一般不遵从线性定律.渗透率有如下表达［5］

式中Kg是低密度下对气体的渗透率；K是对液体或高密度气体的渗透率；λ是在该测量压力下气体的平均自由程；c是接近于1的比例系数；b是依赖于分子平均自由程λ和管径r的常数.在所考虑的吸附问题的特定压力范围，渗透率接近于常数.

气体运动的连续性方程为

（8）式表明，速度是与压力梯度有关的常数.

1.2 吸附质的平衡方程

床层吸附动力学原理是固体吸着剂实现净化和回收的基础.床层吸附动力学的任务之一，是确定在任意给定的时间内，某一截面吸附剂层的吸附容量的利用程度，以及充满在颗粒之间的自由空间内的气体或液体中吸附物的浓度与吸附过程实现条件的关系.现考虑混合气体通过吸附层的流动.设流动方向为X轴正向，以a（x，t）表示单位体积的吸收剂所吸收的气体量，并用u（x，t）表示在x处的吸收剂孔隙中的气体浓度．相对于一般的液体渗透而言，假设气体速度v较大，且扩散过程在气体传送中不起重要作用．那么，对t1到t2时段x1到x2的一层吸收剂，有如下平衡方程

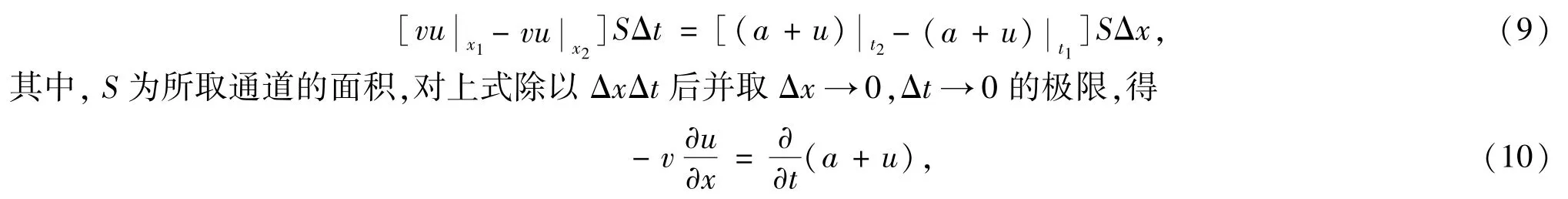
方程左端代表单位长度单位时间内由传送积累的气体量，右端是吸收的气体的浓度与孔隙中的气体的浓度的增加量.

1.3 吸附过程模型方程

吸附速率，或单位时间内被单位体积的吸附层所吸附的物质的量，按下列的吸着动力学方程求得［1］

2 模型方程的求解

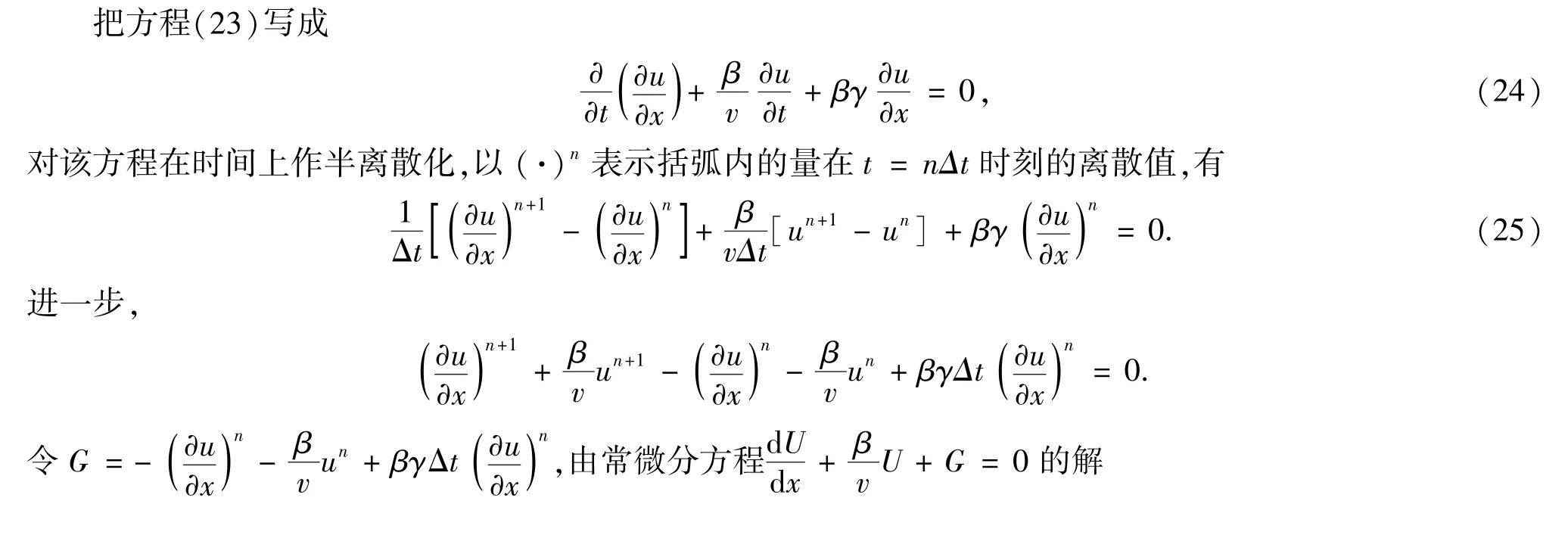
给出u在n＋1时间层X轴上各点的值.

3 结果分析

考虑混合气体通过一厚度为L＝100 cm的吸附层.设气流以速度v＝100 cm·s－1通过单位截面，且γ＝1.2，β＝10.0，入口处单态氧的浓度为u0＝2×10－5g·cm－3.图2显示了计算得到的t＝0.2 s、t＝0.4 s、t＝0.6 s、t＝0.8 s及t＝1.0 s五个时刻吸附剂吸收的单态氧的浓度分布；图3示出了相应时刻计算得到的气流中单态氧的浓度分布；图4显示了总吸收的单态氧的量随时间的变化.可以看出，图2和图3中曲线都随时间推移而增长；从图示结果可对吸附剂固定床内发生的过程作定性分析.吸附床是装填气流可渗透的固体材料，而含吸附物—单态氧的气流—氦气是不被吸附的气体.设过程开始前吸附剂内单态氧浓度为0，进入的气流内单态氧浓度固定不变.在t＝0的起始瞬时，气流尚未进入床层内，气流中单态氧浓度为u0，吸附剂内单态氧浓度等于0（a＝0）.在起始瞬时，若气流已进入吸附层内，则除迎面层截面（x＝0）外，在吸附床层的各个截面上单态氧浓度仍等于0．迎面层截面上的吸附剂开始吸收单态氧（a≠0），相应地在已进入的单元气流内单态氧的浓度开始下降.单态氧已部分消耗的单元部分随气流进入下一单元体积吸附剂层.在这一层内开始物质的吸收过程.接着第三、第四层…，单元体积相继进入吸着过程.

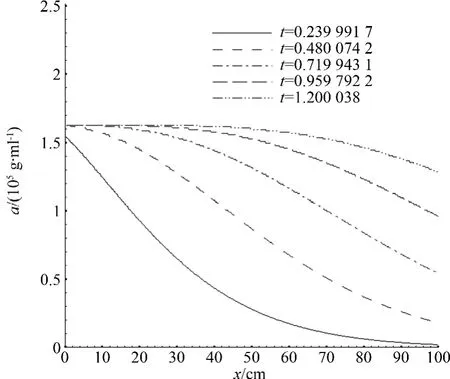
图2 吸附层吸收的氧气浓度Fig.2 Oxygen concentration in adsorption layer

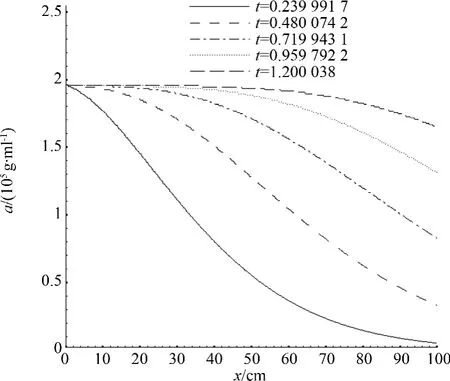
图3 气流中的氧气浓度Fig.3 Oxygen concentration in gases

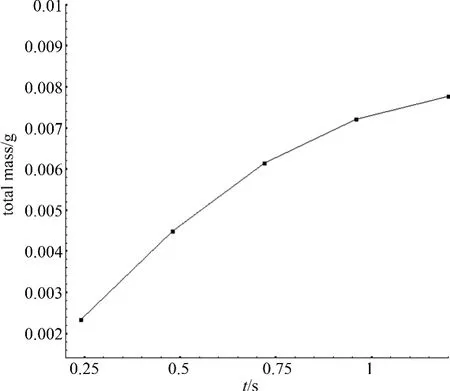
图4 吸收的氧气量随时间的变化Fig.4 Adsorped oxygen mass versus time

考虑某一持续时间内某一吸附层截面（x＝0）上的浓度变化．气流内单态氧的浓度由于新鲜气体的补充，不会发生变化；在整个过程进行的时间内，其浓度为u0．吸附剂内吸附质浓度（吸附量）逐渐增加，在较长时间后达到与u0平衡的值a*0．

同时还可知，在任意的x下浓度随时间的推移而增加；对于任意有限长度的吸附层来说，在t→∞时，气流内单态氧浓度达到原始值u0，吸附剂内单态氧浓度达到与之平衡的值a*0．从图2和图3中可以看出，在t＝1.2 s时接近达到这些平衡值.

4 结论

对COIL中工作气体单态氧的低温吸附问题建立模型.从质量守恒方程导出气体压力降与速度成正比，即在确定的压力梯度下，速度为常数的近似.模型方程由吸附平衡方程和吸附动力学方程，辅助以亨利等温线方程组成.有如下结论：

1）一般地，气体流过多孔材料时压力梯度不与速度成正比.考虑到被吸收的单态氧在混合气体中所占比例较小，且在吸附过程中释放的热量容易被氦气带走，得出气体的流动速度与压力降近似成正比，且为常数.

2）气体的吸附在多孔床内沿流动方向是逐层进行的，吸附的长时间行为，即要吸附的物质量很大，超过床层的吸附能力时，吸附质——单态氧在气体中保持原入流浓度，在吸附层内达到与之平衡的浓度值.

由于吸附问题的复杂性，本文所建模型是粗浅的，仅适于吸收少量部分气体的问题.其中等温线方程采用的亨利关系式，对吸附过程的初期阶段较适合，如要仔细考虑吸附过程后期阶段及压力变化的影响，需采用更复杂的等温线方程.

［1］郑炽，徐以俊.气体与蒸气的工业吸附 ［M］.北京：化学工业出版社，1958：1－10.

［2］李健博.几种气体在ZSM-5分子筛上吸附的模拟与实验研究 ［D］.天津：天津大学硕士学位论文，2007.

［3］Eppard WM，Mcgrory WD，Godfrey A G，et al.Recent advances in numerical techniques for the design and analysis of COIL systems［J］.AIAA－2000－2576，2000.

［4］Thayer WJ，Fisher C H.Comparison of predicted and measured output from a transverse flow uniform droplet singlet oxygen generator［J］.AIAA 94－2454，1994.

［5］邓英尔，刘慈群，黄润秋，王允诚.高等渗流理论与方法［M］.北京：科学出版社，1996：187－189.

A Model of Single Delta Oxygen Cryosorption

XUE Shesheng，LIShouxian，LIU Yang
（Institute of Applied Physics and Computational Mathematics，Beijing 100094，China）

Cryosorption of oxygen produced in chemical oxygen iodine laser（COIL）is considered.From the view point of mass conservation，a linear relation between gas pressure gradient and gas velocity is used with which gases flows through a zeolite porous bed is obtained.An adsorption balance equation，describing relation of components in gas flow and adsorped components，is established with adsorption dynamics equation.Henry relation is employed as isothermal equation.A set of cryosorptionmodel equations is solved numerically.Oxygen concentration evolution，and long time character of concentrations are given.

cryosorption；porousmaterial；COIL；numerical computation

date：2013－09－13；Revised date：2013－11－25

TN248.5

A

1001-246X（2014）04-0412-05

2013－09－13；

2013－11－25

国家自然科学基金（11371067）资助项目

薛社生（1965－），男，博士，副研究员，从事计算流体力学研究，E-mail：xue_shesheng＠iapcm.ac.cn