气体运动论统一算法在跨流域转动非平衡效应模拟中的应用

蒋新宇， 李志辉， 吴俊林

气体运动论统一算法在跨流域转动非平衡效应模拟中的应用

蒋新宇1，2， 李志辉1，2， 吴俊林1

（1.中国空气动力研究与发展中心超高速研究所，四川绵阳 621000；2.国家计算流体力学实验室，北京 100191）

从考虑转动松弛变化特性的Rykov模型出发，基于Boltzmann模型方程求解跨流域气体运动论统一算法原理与计算规则，采用转动惯量描述气体分子自旋运动，研究考虑转动非平衡影响的Boltzmann模型方程数值求解方法.通过对氮气激波结构、二维钝头体和三维尖双锥跨流域绕流的模拟分析，验证该算法的跨流域一致适用性.

转动非平衡；统一算法；激波结构；钝头体；尖双锥

0 引言

飞行器往返大气层经历连续流、近连续流、滑移过渡流以至高稀薄自由分子流［1］等，不同流域气体热力学性质及绕流状态互不相同.在稀薄过渡流区，由于连续介质假设失效，N-S方程已不能有效描述飞行器绕流流动现象；而基于微观分子运动与碰撞随机统计模拟的DSMC方法因受网格划分、时间步长限制，难以对低Knudsen数高空近连续稀薄流进行数值仿真［2－3］.如何准确模拟近连续滑移过渡流区高超声速气动力／热环境，一直是人们所关心的问题［4－5］.

气体分子运动论的基本方程—Boltzmann方程本身可描述各个流域的气体分子输运现象，通过求解Boltzmann方程可以研究各流域气体动力学问题.但该方程是一个高度非线性积分－微分方程，几乎不可能求出精确解.为避免求解复杂碰撞项，众多学者基于守恒不变量，由数学上较简单的统计和碰撞松弛模型代替Boltzmann方程碰撞项，提出许多气体运动论模型方程.最简单的BGK模型方程于1954年提出，随后，人们发展了多种形式的Boltzmann模型方程，诸如Holway的椭球模型［6］、Shakhov基于BGK方程的修正而得到的高阶推广模型方程等［7］.因此，求解简化的Boltzmann模型方程，是一个较为经济有效的解决途径.李志辉［8－11］从研究建立描述各流域均适用的气体分子速度分布函数方程出发，吸收计算数学指数型积分求解原理，提出气体运动论离散速度坐标法，发展经改进的Gauss-Hermite积分方法等系列离散速度数值积分技术，消除原分布函数对速度空间的连续依赖性，将Boltzmann模型方程化为在各个离散速度坐标点处基于时间、位置空间具有非线性源项的双曲型守恒方程，利用二阶Runge-Kutta方法数值求解源项方程，引入NND格式数值求解对流运动项.基于对气体分子与物面相互作用原理的研究，发展可用于气体分子速度分布函数有限差分求解的气体运动论边界条件数学模型.由此建立求解一维、二维、三维Boltzmann模型方程的气体运动论统一算法，开展跨流域气体绕流数值模拟应用［12－13］.为了研究近空间飞行器跨流域非平衡绕流问题，近年来，基于对转动自由度松弛变化［14］、气体分子运动论Rykov模型［15－16］的研究，在气体分子速度分布函数演化更新求解中考虑转动自由度影响，把气体分子转动能作为分布函数的自变量，在统一算法理论与计算框架下，提出考虑转动非平衡效应Boltzmann模型方程数值算法［17］.本文在此基础上，针对高、低不同马赫数（1.53≤Ms≤25）氮气一维激波结构，不同Knudsen数（10－3≤Kn∞≤10）二维钝头体绕流和三维双锥外形绕流算例，研究考虑转动非平衡效应Boltzmann模型方程在跨流域绕流问题中的模拟应用，计算剖析自由分子流到连续流跨流域中间过渡带非平衡流动规律与绕流现象.

1 控制方程与计算方法

1.1 求解分子速度分布函数方程数值格式

基于转动松弛特性Rykov模型［15－16］，采用转动惯量来描述气体分子的自旋运动，利用分子总角动量守恒作为一个新的碰撞不变量.基于气体分子速度分布函数f＝f（r，ξ，t，e），这里r、ξ分别是位置空间和速度空间的坐标、e为内能，在求解Boltzmann模型方程的统一算法理论框架［8－13］下，引入权因子1和e对速度分布函数所依赖的速度空间进行无穷积分，构建经约化速度分布函数处理［17－18］，考虑转动非平衡影响的Boltzmann模型方程，其无量纲形式为

这里，T∞和T*均为有量纲的值，但B＝T∞／T*是无量纲量．对于氮气N2而言，T*＝91.5 K，1／δ＝1.55．

速度分布函数f0、f1是依赖于时间t、位置空间r和速度空间ξ的函数，需将速度空间离散降维，去掉其对速度空间的连续依赖性.气体运动论离散速度坐标法［8－10，18］通过一套与积分规则相一致的离散速度坐标点分布，用具有N个元素的函数簇代替原分布函数对积分变量的连续依赖性，把模型方程转换为在各离散速度坐标点处彼此独立的关于位置空间和时间的双曲型守恒方程，宏观流动参数则可通过相应于离散速度坐标法的积分求解规则确定.如经速度空间离散处理的速度分布函数方程在计算平面内矩阵形式为

采用文献［9－10，18］所建立二阶有限差分格式，将时间分裂数值计算方法应用于方程（4）式中位置空间的三个对流运动方程和碰撞松弛源项方程进行耦合数值求解，得到在每个离散速度坐标点处直接求解分子速度分布函数的气体运动论数值格式

1.2 边界条件数值处理方法

对于流场边界条件数值处理，按照统一算法基于分子速度分布函数边界处理数学模型［11，13，18］，对于无穷远处来流条件，我们以无量纲的来流宏观参数n∞＝1、U∞、V∞、W∞和T∞＝1所表征的平衡态分布函数确定

第二种，适应系数通过分析氮气中热传导的实验数据得到［15］

2 数值计算结果与讨论

2.1 高、低不同马赫数定常正激波内流动

为检验考虑转动非平衡影响的Boltzmann模型方程统一算法对高、低不同马赫数激波内流动问题模拟能力，计算氮气中激波内流动.为便于比较，引入无量纲参考值［18］：

图1分别绘出马赫数Ms＝1.53、3.2、10、25激波结构无量纲密度ρ*分布，图中GKUA表示统一算法结果，Exp.为来自文献［20］实验数据，GBE为文献［14，21］中的广义退化Botzmann方程解算器计算结果.可看出，对于高、低不同马赫数1.53～25激波内流动密度分布统一算法结果均与实验数据、典型文献模拟值吻合较好.图2绘出考虑转动非平衡影响的Ms＝25强激波内流动密度与温度变化轮廓线，图中实线n表示数密度，虚线T为全局温度，点划线Tt表示平动温度，双点划线Tr表示转动温度.可看出，激波内流动从波前开始，温度先于密度激发，不同模态的温度中平动温度又先于转动温度激发.激发的不同时正好说明了激波流动是一个非平衡变化过程.图中还显示出整个非平衡流动区间中，平动温度总是远高于转动温度，这也表明平动温度的主导地位，造成平动温度轮廓线在临近激波下游过渡区出现严重的非平衡凸起“超出”现象.图1、图2关于弱激波Ms＝1.53到强激波Ms＝25的计算，证实统一算法在计算分析双原子氮气高、低不同马赫数激波内流动问题方面的准确可靠性.

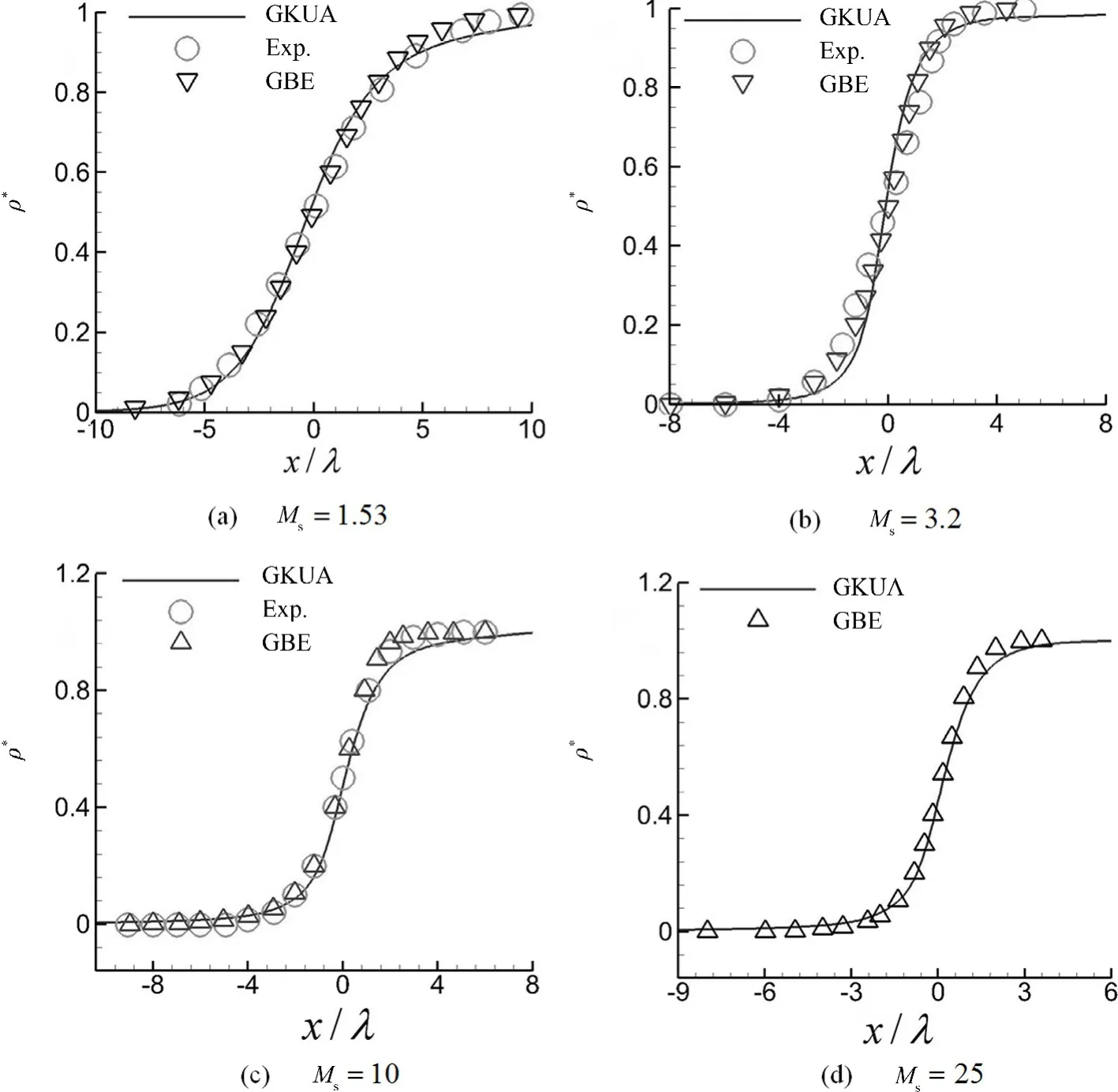
图1 高低不同马赫数下激波内流动密度分布Fig.1 Density distributions in shock wave at various Mach numbers

2.2 二维钝头体全飞行流域绕流

为了研究从自由分子流到连续流跨流域二维绕流流场中的内能非平衡影响，拟定图3所示的一个钝头体［21］外形，其中方形柱段长度是圆头半径的两倍，计算来流马赫数Ma＝3、克努森数Kn＝10、1、0.1、0.001的绕流流场.图4绘出了三种不同Kn数下，钝体绕流流场的密度分布等值线图.可以看出：在Kn＝10时，流场扰动区域很大，没有出现参数强间断形式的激波，流场为稀薄流；在Kn＝0.001时，流场存在明显的激波，扰动无法传播至上游，流场为连续流、近连续流；而在Kn＝1时，可以看到物体前面厚厚的激波强扰动，流场体现为过渡区绕流.通过对自由分子流到连续流全流域的钝头体绕流数值模拟，证明了统一算法的跨流域一致适用性.

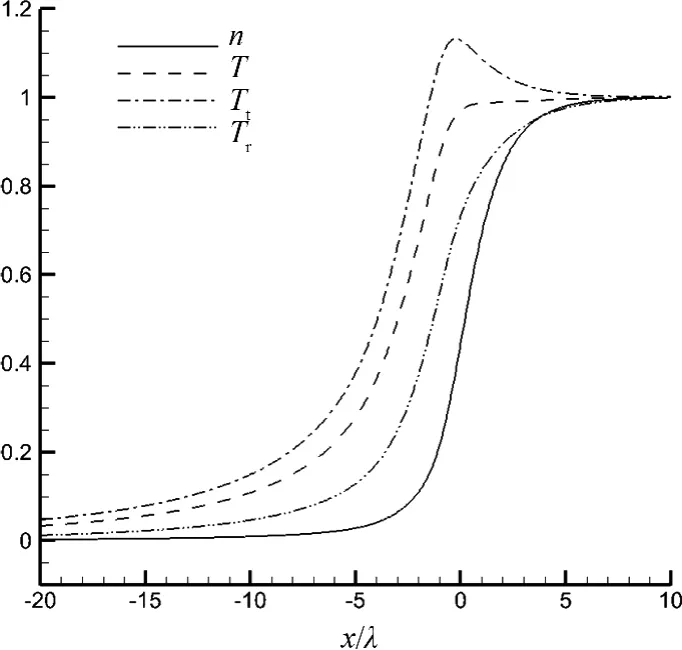
图2 Ms＝25氮气激波结构内流动密度分布与平动、转动和全场温度分布Fig.2 Distribution of density，translational temperature，rotational temperature and global temperature in nitrogen shock wave at Ms＝25

图3 钝头体外形尺寸示意图Fig.3 Blunt body geometries

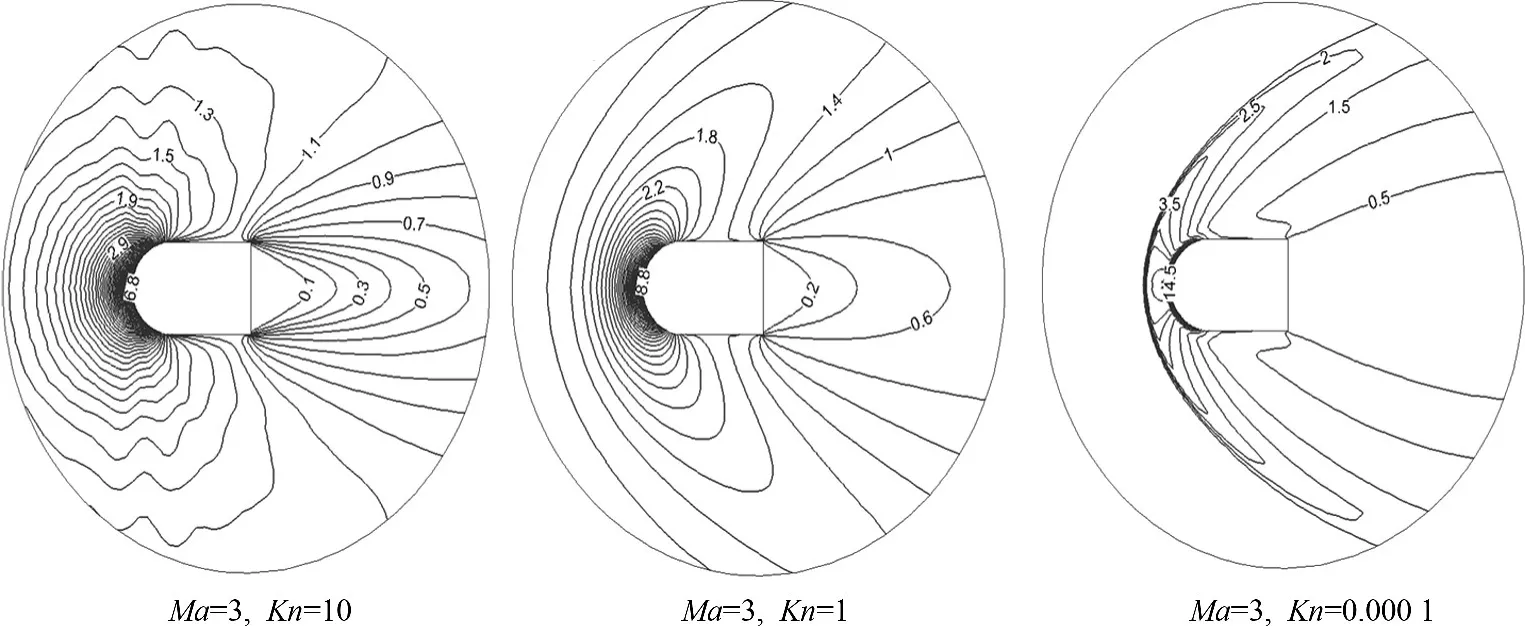
图4 不同Kn数下钝体绕流的密度分布Fig.4 Density contours around a blunt body

为了剖析过渡区流动的非平衡效应，图5、图6分别绘出了Kn＝1与Kn＝0.001两种状态对应的绕流流场温度分布，其中图（a）表示平动温度等值线、图（b）表示转动温度等值线.可以看出：在Kn＝0.001对应的近连续流区，平动温度与转动温度分布趋于一致，流场等值线结构基本无差别，流动可以认为是平衡流；而Kn＝1对应的高稀薄流区，平动温度与转动温度彼此差别较大，计算得到的物体前部高温区平动温度最大值约为3，而转动温度最大仅1.6左右，两者相差近一倍，流场表现出强烈的稀薄非平衡特性.

2.3 双锥外形体跨流域绕流

为了检验考虑转动非平衡影响的Boltzmann模型方程统一算法对三维飞行器跨流域绕流模拟能力，拟

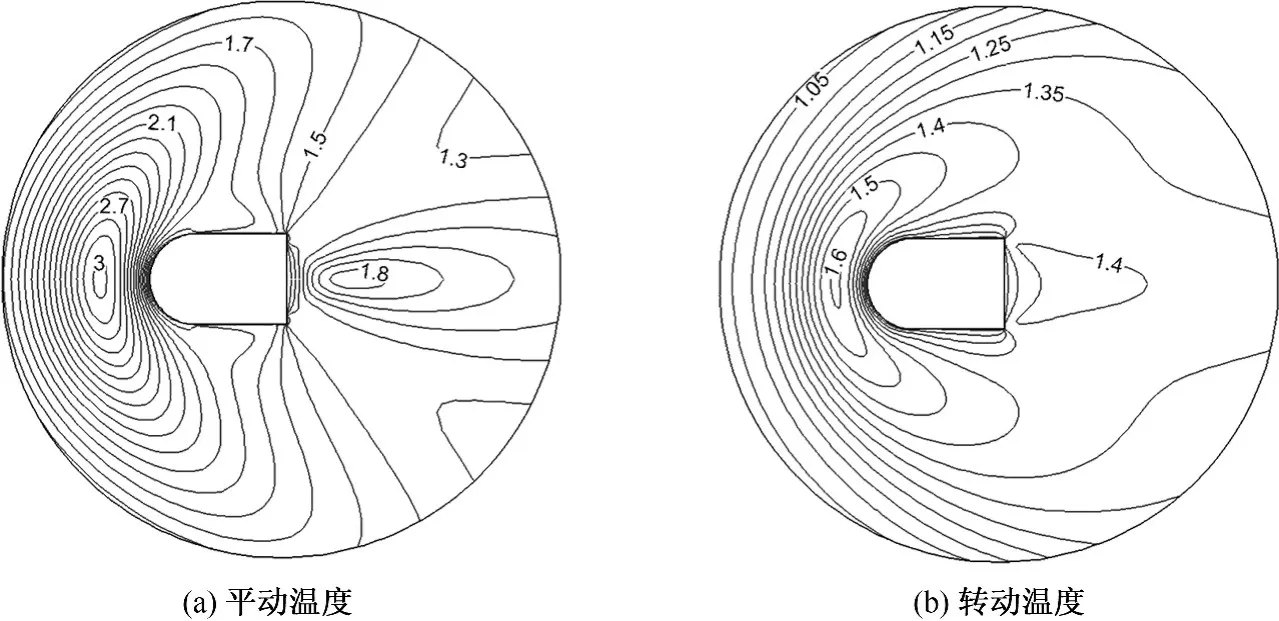
图5 钝头体绕流（Ma＝3，Kn＝1）流场温度分布等值线Fig.5 Temperature contours around a blunt body at Ma＝3，Kn＝1

图6 钝头体绕流Ma＝3，Kn＝0.001流场温度分布等值线Fig.6 Temperature contours around a blunt body at Ma＝3，Kn＝0.001

定图7所示双锥外形.为了与文献［22］使用GBE解算器计算高稀薄流区来流马赫数Ma＝3、克努森数Kn＝1的上述尖头双锥外形绕流状态分析比较，本文计算了该外形以Ma＝3通过稀薄过渡区Kn＝1、0.1的绕流流场.图8绘出了统一算法计算上述尖双锥外形绕流Ma＝3、Kn＝1驻点线密度分布与文献［22］Wilson计算结果（符号Δ表示）的对比，可看出两种方法有较好的一致，证实考虑转动非平衡效应的统一算法用于计算三维飞行器跨流域绕流问题的可行性.图9绘出Ma＝3、Kn＝1时的稀薄过渡流区双锥绕流流场的

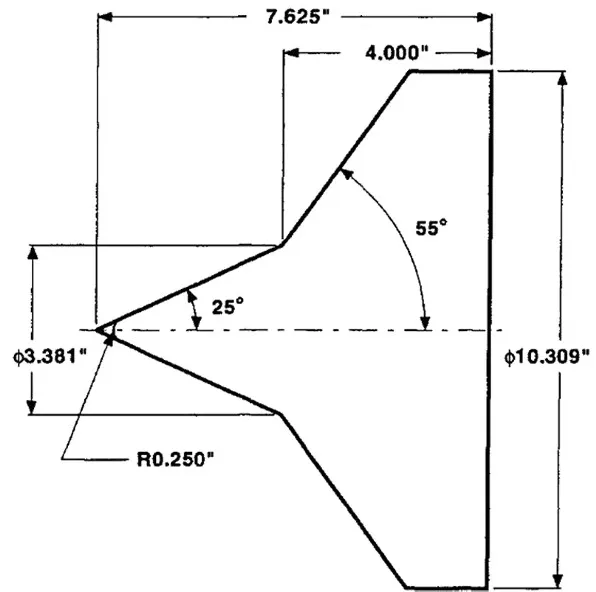
图7 双锥外形示意图Fig.7 Bicone geometries

图8 Ma＝3，Kn＝1驻点线密度分布Fig.8 Density distribution along the stagnation line at Ma＝3，Kn＝1

图9（a）平动温度和图9（b）转动温度分布，可以看出两者有较大的差距，这体现了高Kn数稀薄过渡流区存在严重的流动非平衡，说明了在稀薄流区考虑转动平衡效应的必要性.图10绘出Kn＝1和Kn＝0.1两种状态下尖锥绕流流场全局温度分布.从图中可以看出，Kn＝1时，流动呈现较强的稀薄流特征，激波强扰动不明显，流动参数没有强间断，物体前方扰动区域范围很大；而Kn＝0.1时，流动趋近物体前端出现激波强扰动现象.

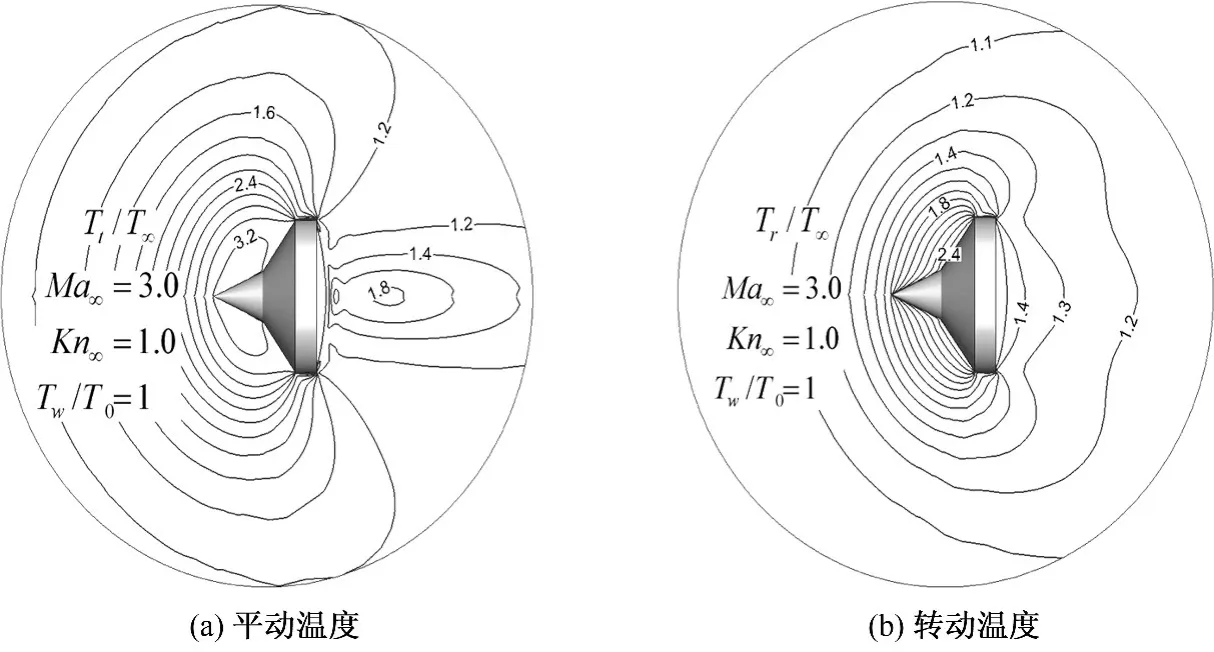
图9 Ma＝3，Kn＝1尖双锥绕流温度分布Fig.9 Temperature contours around bicone at Ma＝3，Kn＝1

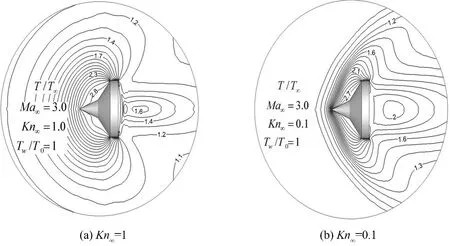
图10 不同努森数尖双锥绕流全局温度分布Fig.10 Temperature distributions around bicone at different Kn

我行还计算分析了该外形在Ma＝3、Kn＝0.000 1连续流区的绕流流场.如图11所示.从密度、温度、马赫数等参数的等值线图上均可以明显看出斜激波和弓形激波的相互干扰.从热流云图上可以看出，脱体弓形激波强度远强于第一个锥产生的附体斜激波，热流峰值出现在弓形激波处和斜激波后的附面层内，说明飞行器在第一个锥面存在较大热流分布，需要考虑热防护，该图直观再现了双锥外形连续流区绕流存在斜激波和弓形激波相互干扰的复杂流动结构，计算结果与理论分析相吻合.从马赫数等值线图上也可以看出该绕流的简要流动特征：远前方气流绕流第一个锥时会产生一道较弱的斜激波，经斜激波压缩后气流速度降低，但仍然是超音速流动，气流继续向前绕流第二个锥时会产生一个脱体的弓形激波，两道激波在两个锥面结合处会聚相遇相互挤压影响，产生一道更强的正激波，波后气流变为亚音速.当气流完全绕过锥体，在第二个锥面结束处因流动急剧膨胀而产生一束膨胀波系，重新将绕流气体加速到超音速往后流去.

3 结论

基于对气体分子转动自由度和Rykov模型，应用稀薄流到连续流气体运动论统一算法数值求解考虑转动非平衡影响的Boltzmann模型方程.针对不同马赫数定常正激波结构、二维钝头体全飞行流域绕流、尖双锥外形体跨流域绕流问题计算分析，得到如下结论：

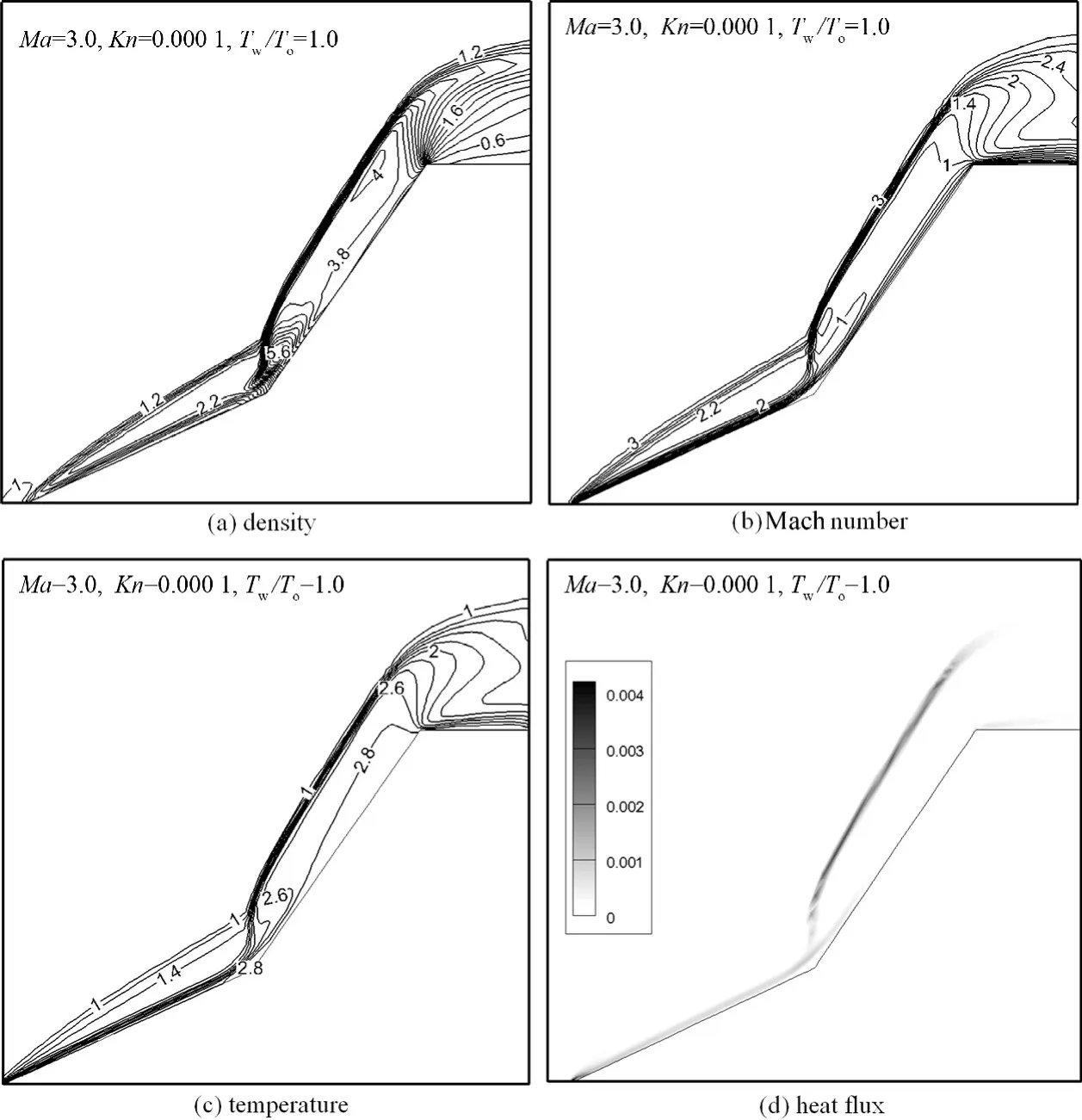
图11 Ma＝3，Kn＝0.000 1尖双锥绕流流场Fig.11 Flow around bicone at Ma＝3，Kn＝0.000 1

1）通过对宽广马赫数范围内（1.53≤Ms≤25）考虑转动非平衡影响的氮气激波结构计算结果与实验数据、典型文献模拟值比较分析，验证了考虑转动非平衡影响的统一算法对求解强、弱激波一维流动问题的准确可靠性，并分析显示了高超声速情况下激波结构中的非平衡流动特征与变化规律.

2）通过对二维钝头体外形从自由分子流到连续流跨流域绕流流场的模拟研究，显示了跨流域不同流动特征，验证了考虑转动非平衡影响的统一算法对全飞行流域模拟计算的一致适用性.通过对比分析绕流流场平动温度与转动温度分布，证实来流Kn数越高，流动非平衡效应越明显.

3）通过对尖双锥外形跨流域绕流状态的计算分析，描述了稀薄气体转动非平衡效应和连续流区的激波干扰现象.验证了考虑转动非平衡效应的统一算法对三维复杂飞行器跨流域绕流问题的模拟能力.

本文工作仅考虑转动非平衡影响的Boltzmann模型方程统一算法在跨流域绕流问题方面的初步应用与计算检验，将其应用于跨流域复杂高超声速气动力／热绕流问题以及考虑转动能与振动能、混合气体非平衡效应的适应性研究等，还有待进一步深入.

致谢：本文工作得到国家自然科学基金重大研究计划‘近空间飞行器的关键基础科学问题'重点支持项目（91016027）资助，大部分并行计算在国家超级计算天津中心和国家超级计算济南中心完成，特此表示感谢.

［1］Qian X S.Superaerodynamics，mechanics of rarefied gases［J］.Journal of Aeronautics Science，1946，13（12）：653－664.

［2］Koppenwallner G，Legge H.Drag of bodies in rarefied hypersonic flow［C］∥Progress in astronautics and aeronautics：Thermophysical aspects of reentry flows，New York，AIAA Paper 85－0998，1985，103：44－59.

［3］李志辉，吴振宇.阿波罗指令舱稀薄气体动力学特征的蒙特卡罗数值模拟 ［J］.空气动力学学报，1996，14（2）：230－233.

［4］Whitehead A J.NASP aerodynamics［J］.AIAA Paper 89－5013，1989.

［5］庄逢甘，崔尔杰，张涵信.未来空间飞行器的某些发展和空气动力学的任务 ［C］∥中国第一届近代空气动力学与气动热力学会议论文集，2006，8：1－12.

［6］Holway JLH.New statisticalmodels for kinetic theory，Methods of construction［J］.Phys Fluids，1966，9（9）：1658－1673.

［7］Shakov E M.Generalization of the Krook kinetic relaxation equation［J］.Fluid Dynamics，1968，3（1）：95－96.

［8］李志辉，张涵信.稀薄流到连续流的气体运动论统一数值算法初步研究 ［J］.空气动力学学报，2000，18（3）：251－259.

［9］李志辉，张涵信.稀薄流到连续流的气体运动论模型方程算法研究［J］.力学学报，2000，34（2）：145－155.

［10］Li Z H，Zhang H X.Study on gas kinetic unified algorithm for flows from rarefied transition to continuum［J］.J of Comput Phys，2004，193：708－738.

［11］Li Z H.Gas-kinetic unified algorithm for re-entering complex problems covering various flow regimes by solving Boltzmann model equation［M］∥Jason H.Advances in spacecraft technologies，InTech Publisher，2011：273－332.

［12］Li Z H，Zhang H X.Gas-kinetic numerical studies of three-dimensional complex flows on spacecraft re-entry［J］.JComput Phys，2009，228：1116－1138.

［13］李志辉，张涵信.基于Boltzmann模型方程各流域三维复杂绕流问题统一算法研究 ［J］.中国科学，2009，39（3）：414－427.

［14］Agrwal R K，Chen R，Cheremisin F G.Computation of hypersonic shock wave flows of a diatomic using the generalized Boltzmann equation［C］.AIAA 2007－4541，39th AIAA Thermophysics Conference，Miami，FL，June 25－28，2007.

［15］Rykov V A.Model kinetic equation of a gaswith rotational degrees of freedom［J］.Fluid Dynamics，1975，（10）：959－966.

［16］Rykov V A，Titarev V A，Shakhov E M.Shock wave structure in a diatomic gas based on a kinetic model［J］.Fluid Dynamics，2008，43（2）：316－326.

［17］李志辉，吴俊林，彭傲平，张涵信.考虑转动非平衡效应Boltzmann模型方程统一算法与跨流域绕流问题模拟研究［C］∥第七届全国流体力学学术会议论文集，CSTAM2012-B03-0195，11月12～14日，广西桂林，2012.

［18］李志辉.从稀薄流到连续流的气体运动论统一数值算法研究［D］.中国空气动力研究与发展中心研究生部，2001.

［19］吴俊林，李志辉，蒋新宇.考虑转动能影响的一维／二维Boltzmann-Rykov模型方程数值算法应用研究 ［J］.计算物理，2013，30（2）：329－339.

［20］Alsmeyer H.Density profiles in argon and nitrogen shock wavesmeasured by the absorption of an electron beam.［J］.JFluid Mech，1976，74：497－513.

［21］Chen R，Agrwal R K，Cheremisin F G.Computation of supersonic flow past2-D bodies using a Boltzmann solver［C］.AIAA 2005－1102.

［22］Wilson C D，Agarwal R K，Tcheremissine F G.Computation of hyersonic flow of a diatomic gas in rotationa nonequilibrium past3D blunt bodies using the generalized Boltzmann equation［C］.AIAA 2009－3836.

Application of Gas-K inetic Unified Algorithm Covering Various Flow Regimes for Rotational Non-equilibrium Effect

JIANG Xinyu1，2，LIZhihui1，2，WU Junlin1
（1.China Aerodynamics Research and Development Center，HAI，Mianyang 621000，China；2.National Laboratory for Computational Fluid Dynamics，Beijing 100191，China）

With gas-kinetic unified algorithm （GKUA）based on Boltzmann equation for various flows regimes，rotational nonequilibrium effect is investigated in Rykov model，in which spin movement of gas molecules is described with moment of inertia. Numericalmethod of Boltzmannmodel equation involving rotationalnon-equilibrium effect is developed.Nitrogen shock wave structure，flows around a 2D blunt-head body and flows around a 3D tine bicone are simulated to validate themethod in various flows regimes.

rotational non-equilibrium；GKUA；shock wave structure；blunt-head body；tine bicone

date： 2013－03－17；Revised date： 2013－07－17

V211.3

A

1001-246X（2014）04-0403-09

2013－03－17；

2013－07－17

国家自然科学基金（91016027）资助项目

蒋新宇（1987－），男，硕士，助理工程师，从事稀薄气体动力学研究

李志辉，E-mail：zhli0097＠x263.net