求解双曲守恒律方程的高分辨率熵相容格式

任 炯， 封建湖， 刘友琼， 梁 楠

（1.长安大学理学院， 陕西西安 710064；2.西北工业大学航空学院流体力学系， 陕西西安 710072）

求解双曲守恒律方程的高分辨率熵相容格式

任 炯1，2， 封建湖1，*， 刘友琼1， 梁 楠1

（1.长安大学理学院， 陕西西安 710064；2.西北工业大学航空学院流体力学系， 陕西西安 710072）

为提高熵相容格式的精度，利用限制器机制构造高分辨率格式，将构造的通量限制器插入熵相容格式，得到一类高分辨率熵相容格式.构造Euler方程高分辨率熵相容格式时，对熵相容格式中的几个参数做简单调整，提高了接触间断处的分辨率.将所得格式的数值结果与熵相容格式的数值结果比较表明，构造的高分辨率熵相容格式具有稳健和基本无振荡等特性.

双曲守恒律；熵相容格式；限制器；高分辨率

0 引言

在一维情况下，双曲守恒律方程的一般形式为

其中（x，t）∈R×R＋，u：R×R＋→RN（N≥1）是守恒变量，f（u）是通量函数.该类方程作为流体力学中重要的物理模型，在航空航天、气象、海洋等科学工程领域都有广泛的应用，其数值求解的方法一直是国内外众多学者致力于研究的方向.对于非线性双曲守恒律方程，即使所给的初始条件光滑，其解在时间推进的某个时刻也可能会出现间断，产生激波.间断解的出现使双曲守恒律方程的解违背了古典解的理论，于是Lax在1954年提出了弱解［1］的概念，允许间断解存在，但弱解不唯一，这就需要从方程的实际物理背景出发给出限制条件来确定物理相关的解.这个工作也是Lax完成的，他从物理学中的热力学第二定律出发，提出：如果弱解u满足熵稳定条件［2］

则u就是唯一的具有物理意义的解，其中E（u）是u的凸函数，满足E″（u）＞0，被称为熵函数，F（u）称为熵通量函数．满足式（2）的E（u）和F（u）被称为熵对.为了满足熵稳定条件，Tadmor首先研究了熵稳定和数值粘性之间的关系，在文献［3］和［4］中通过引入熵变量和熵势的概念，构造了一类二阶熵守恒格式，该格式的数值通量保持总熵不变，适用于光滑解的计算，但是当有间断解出现时，由于熵守恒格式缺乏熵的耗散机制，使其数值解表现了严重的不稳定性，这个特点可由第3节中的数值算例直观说明.在此基础上Tadmor又提出：一个三点格式只需含有比熵守恒格式更多的粘性则是熵稳定的.所以要达到熵稳定，只需在该熵守恒格式的基础上适当地加入一些粘性.但究竟应该添加多少数值粘性，一直以来都是相关研究人员思索的问题，其中Tadmor，Zhong［5－6］和Roe都做了相应的工作，但以Roe的方法最为理想和实用，Roe是在熵守恒格式的基础上加上他提出的Roe格式的数值粘性，获得了一阶精度的熵稳定ERoe格式［7］，随后在2009年，他和Ismail进一步通过分析得到：解在跨过激波时产生了激波强度立方倍的熵增，在此基础上发展了对数值粘性项更精确量化的熵相容格式［8］，但由于其数值粘性项只有一阶精度，从而导致该格式比熵守恒格式的精度有所降低.鉴于此，本文采用传统的构造二阶总变差减少（total variation diminishing，简称TVD）格式的方法［9－10］，即利用通量限制器机制提高熵相容格式的精度，达到高分辨率的要求.本文通过推广常用的Superbee限制器构造了新的通量限制器，并利用该限制器构造得到高分辨率熵相容格式.由于构造的通量限制器的曲线落在二阶TVD区域内，且过（1，1）点（见图1（a）），所以能够保证新构造的高分辨率熵相容格式满足二阶精度，并且在限制器的开关调节作用下，该格式能够达到自适应性：在解的光滑区域使用二阶精度熵守恒格式，同时避免非物理解的产生；而在间断区域采用熵相容格式，保证有足够的数值粘性抑制振荡.另外本文在构造Euler方程高分辨率熵相容格式时，对其相应的熵相容格式中的几个参数做了简单调整，以改善接触间断处的捕捉效果.最后在第3节通过几个数值算例直观形象地说明了新格式具有稳健性、高精度性和无振荡性等特点.

本文采用均匀网格上的半离散有限体积格式

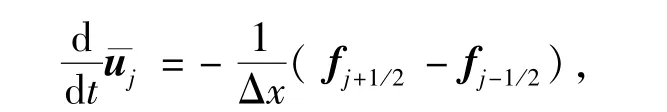
用Δx表示空间步长，Δt表示时间步长，由于该格式与时间相关，所以时间方向的离散可以采用高精度的方法.数值算例在时间演化上采用三阶Runge-Kutta方法［11］：

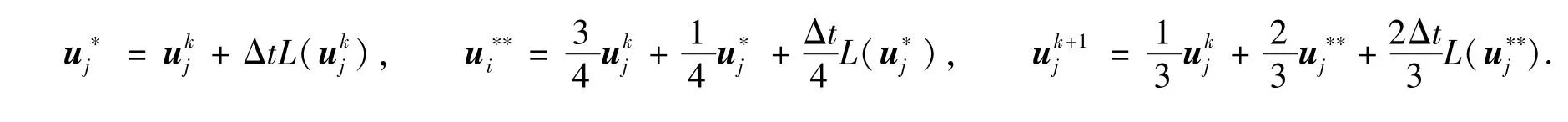
1 通量限制器的构造

对原始的Superbee限制器［12］

式（3）中的α，β，γ这三个参数在各自的范围内可以连续变化，从而产生了一类限制器，我们将此类限制器称为广义Superbee限制器，简记为GSbee类限制器.显然，这类限制器都在Sweby［14］给出的限制器的二阶TVD区域（见图1（a））内，且都满足φ（1）＝1（即过（1，1）点），能达到二阶的要求，随着α，β，γ的连续变化，GSbee类限制器覆盖了整个二阶TVD区域.将这类限制器应用于下节将研究的标量高分辨率熵相容格式在一维Burgers方程间断初值问题上进行大量的数值试验后，发现对于该问题，参数α，β，γ的变化使Gsbee类限制器的功效表现出某些规律：

1）当固定β和γ，α变化：α越大限制器功效越好；

2）当固定α和γ，β变化：β越大限制器功效越好；

3）当固定α和β，γ变化：γ越小限制器功效越好；

为简便，这个试验过程就不一一展示了，而在此，基于以上试验结论的启发，我们分别取α，β，γ的极限，即α＝1，β＝2，γ＝1，得到一个新的限制器：

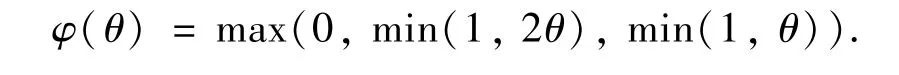
这个限制器可以简化为

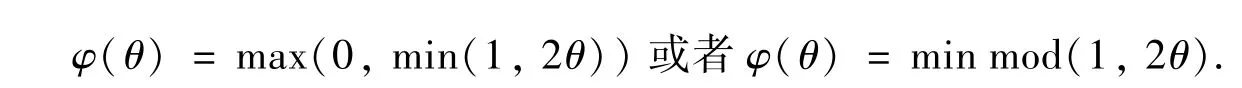
此时，该限制器的形式类似于Minmod［15］限制器

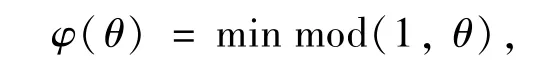
且容易看出Superbee和Minmod限制器都是GSbee类限制器的特殊情况，即

当α＝1，β＝2，γ＝2时，是Superbee限制器；

当α＝1，β＝1，γ＝1时，是Minmod限制器.

在二阶TVD区域内，当0＜θ≤1时，新的限制器是Superbee限制器的部分，当θ＞1时，是Minmod限制器的部分，所以将该新的限制器称为S-M限制器（其中S是Superbee的首字母，M是Minmod的首字母）.Superbee限制器、Minmod限制器和S-M限制器各自在二阶TVD区域中的曲线分别如图1（b）－（d）中的粗黑线所示.

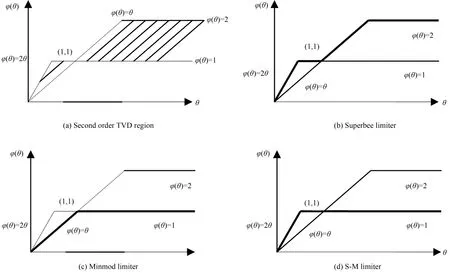
图1 二阶TVD区域和限制器图示Fig.1 Second order TVD regions and limiters

从图1（d）可以看到S-M限制器在二阶TVD区域的边界上，且通过点（1，1），能够保持格式的二阶精度.为方便于下节构造高分辨率熵相容格式和在编程实现时减少逻辑语句的输入，我们将S-M限制器用下面的形式表示

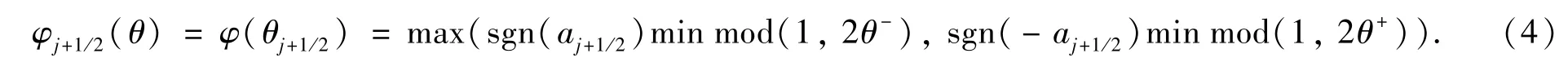
2 高分辨率熵相容格式

2.1 一维标量守恒律方程

2.1.1 熵守恒格式

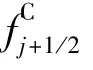
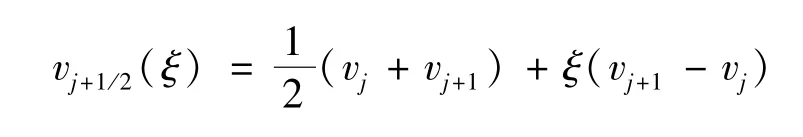
的积分形式［3－4］

Tadmor同时证明了熵守恒格式具有二阶精度.

2.1.2 熵相容格式

熵守恒格式保持了总熵不变，而要满足熵稳定，总熵必须有所耗散，Ismail［8］通过在熵守恒通量的基础

Tadmor在文献［3－4］中由该积分形式出发推导出数值通量满足熵守恒的条件

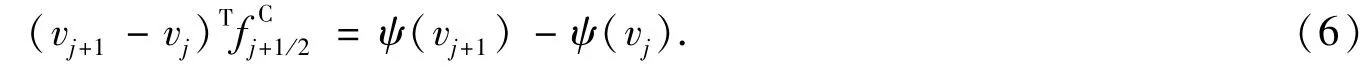
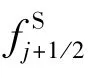
为了更好地推广到方程组的情况，（8）式也可以写成如下形式［8］

其中，符号［·］＝（·）j＋1－（·）j，¯a＝（aj＋aj＋1）／2，aj＝f′（uj）．但是这个迎风项的耗散量却不足以抵消解在跨过激波时所产生的激波强度立方倍的熵增，于是Ismail在上述熵稳定格式（9）的迎风数值粘性项的平均特征速度中补充了一个与特征速度差分的绝对值成比例的量来使熵的耗散更精确，从而得到了熵相容通量

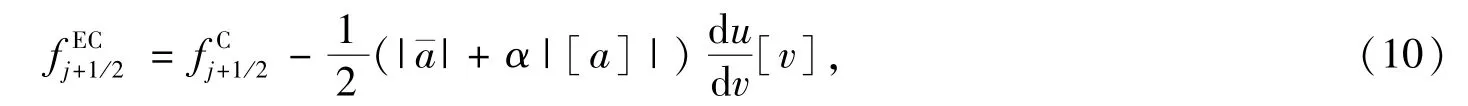
其中，上角标E为熵Entropy的缩写，C为相容Consistent的缩写，α＝1／6，熵相容格式是目前对熵的变化估计得最精确的一种熵稳定格式，但是由于其数值粘性项只有一阶精度，所以导致熵相容格式的精度比熵守恒格式有所降低.

2.1.3 高分辨率熵相容格式

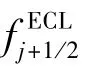
这虽然不影响格式的自适应性，但可能影响限制器的作用范围，幸运的是我们在第2节构造的S-M限制器（4）满足φ（θj＋1／2）≤1，所以完全可以不用考虑加绝对值的问题，因此本文将采用格式（12）进行数值试验，并将该格式称为ECL格式.需要进一步说明的是该格式是在原始熵相容格式的基础上通过限制器的开关作用合理地调节解在各个区域上的熵的耗散量，并没有改变熵的耗散方向.目前还无法从理论上严格证明格式（12）和（13）的稳定性，但是数值算例中并没有出现违反熵条件的现象.另外需要注意的是，文献［10，14］中基于一阶迎风格式和二阶Lax-Wendroff格式构造高分辨率格式时，提到：为尽可能减少格式的数值耗散，提高对间断的分辨率，需要最大化含有限制器的反扩散通量（即限制器曲线需尽可能靠近二阶TVD区域的上边界），而从（13）式看到，本文构造的高分辨率熵相容格式中，含有限制器的通量是格式的耗散通量，所以在满足TVD条件的情况下，若要减少格式的耗散，就应该最小化耗散通量（即限制器曲线需尽可能靠近二阶TVD区域的下边界）.基于此分析，再结合图1（d）中S-M限制器的曲线，我们认为：利用S-M限制器构造高分辨率熵相容格式是合理的.第3节的数值算例部分进一步对此估计做了数值上的验证.

对于一维Burgers方程

2.2 一维Euler方程

考虑气体动力学Euler方程

其中u＝［ρ，ρu，E］T是守恒型向量，f（u）＝［ρu，ρu2＋p，u（E＋p）］T是通量函数．ρ，u，p和E分别为密度、速度、压强和总能，状态方程为p＝（γ－1）（E－（ρu2）／2），γ＝1.4是比热比，是声速.选用Euler方程的熵对E（u）＝－ρS和F（u）＝－mS，其中m＝ρu是动量，S＝ln（pρ－γ）是Euler方程的熵，熵变量为

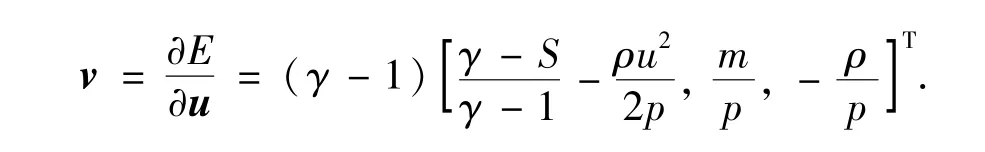
2.2.1 熵守恒格式

本文采用Roe的方法［8］得到Euler方程的熵守恒数值通量

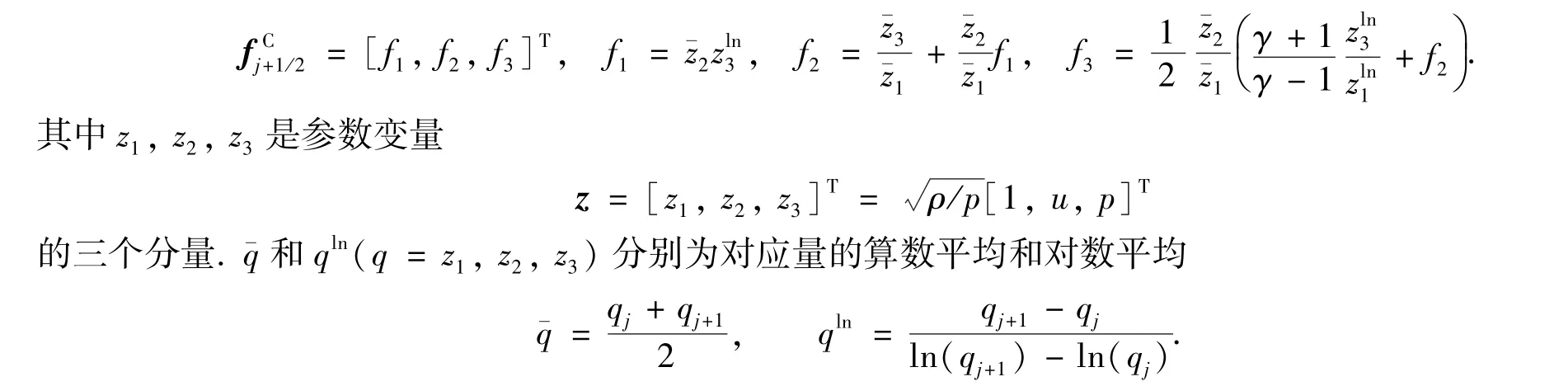
关于对数平均的计算详见文献［8］.

2.2.2 熵相容格式

与标量情形类似，Ismail在Euler方程的熵稳定通量［7］本文将在下小节采用此通量进行高分辨率格式的构造，其中是Euler方程的右特征向量矩阵（详见文献［8］）.

2.2.3 高分辨率熵相容格式

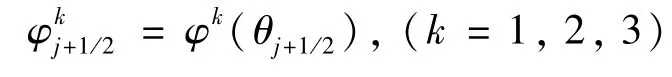
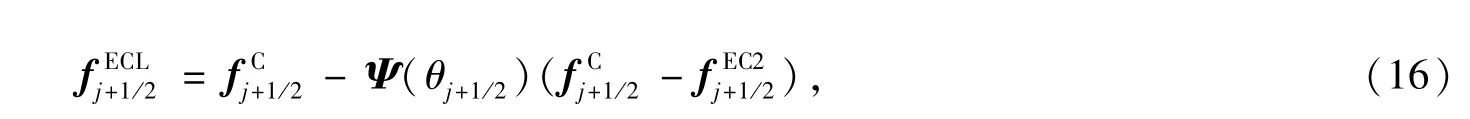
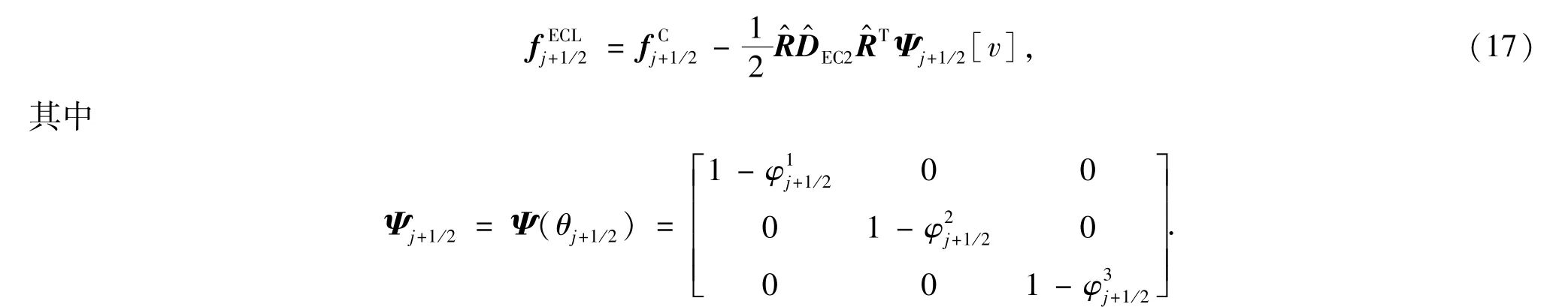
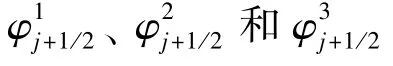
3 数值算例

我们以熵守恒和熵相容格式的数值结果作为参照来说明新的高分辨率熵相容格式的特性；同时也说明我们在第2节构造的S-M限制器（4）可以用来构造高分辨率熵相容格式.

符号约定：

C：熵守恒格式；EC：标量熵相容格式（10）；EC2：Euler方程组熵相容格式（15）；ECL：标量高分辨率熵相容格式（12）；EC2L：Euler方程组高分辨率熵相容格式（17）；Exact：每个算例的精确解.

3.1 标量数值试验

3.1.1 一维Burgers方程连续初值问题（精度测试）

考虑一维Burgers方程的初值问题，在区域［－2，2］上定义初始条件为

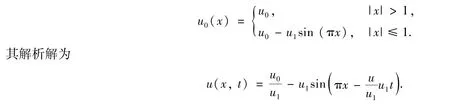
取u0＝0，u1＝0.5，CFL＝0.4，空间网格数为N＝40，采用周期边界条件，图2（a）和（b）分别给出了时间t＝0.32和t＝0.96的数值结果图，且每个图中都分别画出了熵相容格式EC和高分辨率熵相容格式ECL的数值解以及精确解，从这两幅图我们可以看到，在解的光滑区域，两种格式对解的捕捉效果相似，但当解的梯度变大时，ECL格式相对EC格式表现出了更锐利的效果，并且在表1中，通过两种格式精度的比较，也说明了通过通量限制器构造的高分辨率熵相容格式在一定程度上能够提高熵相容格式的精度.

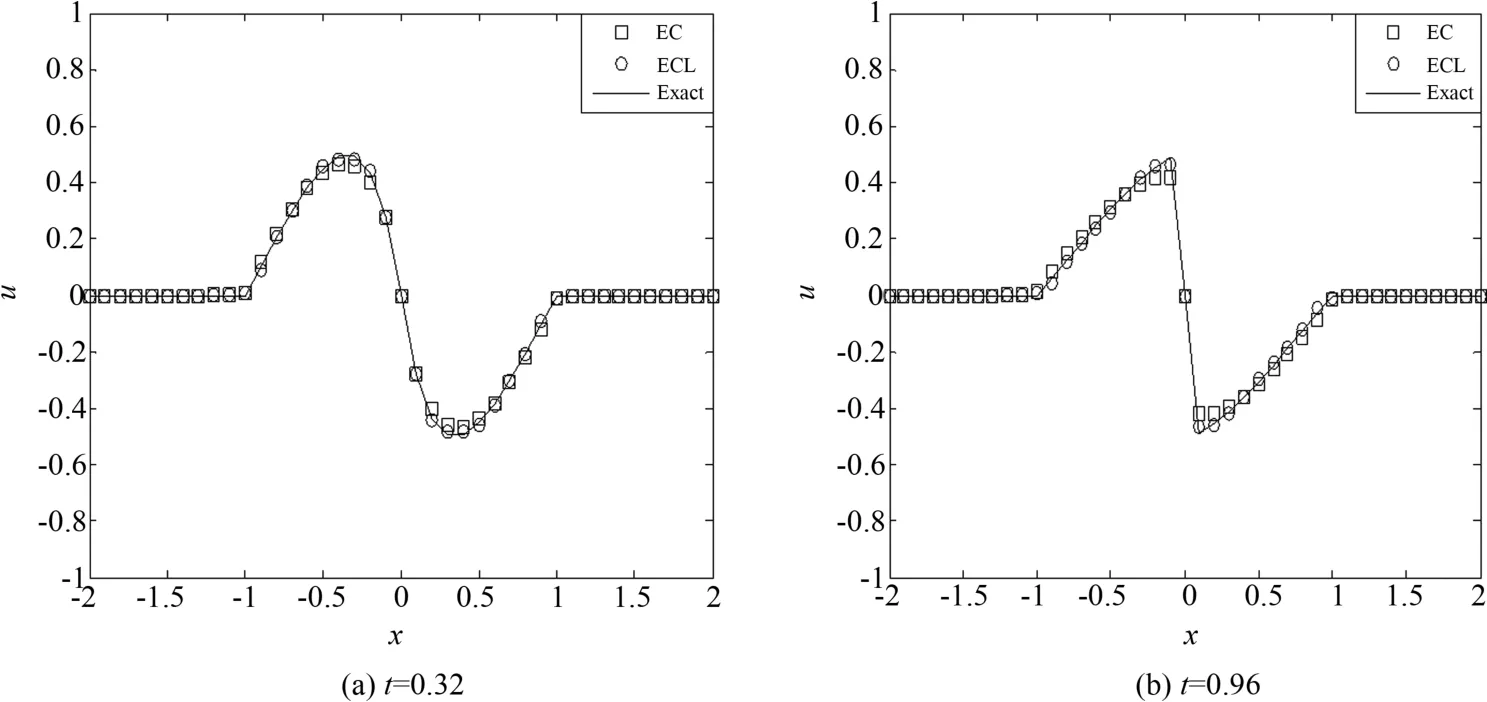
图2 Burgers方程连续初值问题的数值结果Fig.2 Numerical results of continuous IVP of Burgers equation（N＝40）

表1 初值问题3.1.1在时间t＝0.32和t＝0.96的误差的L1－范数Table 1 Initial value problem 3.1.1，L1-norms of errors at t＝0.32 and t＝0.96

3.1.2 一维Burgers方程间断初值问题

在区域x∈［－1，1］上定义初始条件

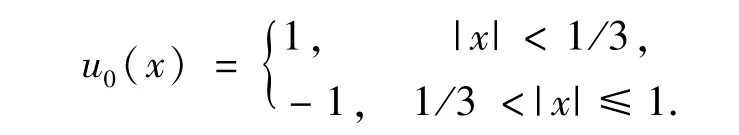
采用周期边界条件，取CFL＝0.4，空间网格数为N＝50，计算到时间t＝0.3．这个问题的精确解主要包括两部分：左边由－1到1产生了一个稀疏波，右边由1到－1产生了一个定常激波.对本问题，我们采用了熵守恒C格式、熵相容EC格式和高分辨率熵相容ECL格式进行数值试验，其结果见图3，图3（a）为C的结果，图3（b）为EC的结果，图3（c）为ECL的结果，可以看到在x＝1／3的激波位置，熵守恒格式表现了较强的色散效应（即产生了强烈的振荡），这是由于熵守恒格式没有任何耗散机制的缘故；而EC格式对此现象进行了完美的修正，这正是熵相容格式在熵守恒格式基础上添加合适数量的数值粘性所起的作用，只是由于数值粘性项只有一阶精度，所以使得EC格式的精度相对C格式有所降低，也使得稀疏波段抹平较为严重；基于前面两种格式的特点，本文构造的ECL格式在稀疏波段和波头、波尾处都比EC有很大的改善，且同时保持了EC格式对激波的良好捕捉效果，无振荡的产生，满足高分辨率的特点.通过观察图3 （d）中三种格式的总熵ΔxΣiu2i／2随时间的变化及其和准确解总熵变化的比较，可以看到C格式的总熵不变，保持熵守恒，而EC和ECL的总熵都是耗散的，保证了熵稳定，且其耗散都多于精确解的耗散，所以都有抹平现象，但相对ECL，EC格式的耗散更多，抹平得也较为严重.

3.2 一维Euler方程组数值试验

3.2.1 一维Euler方程Lax激波管问题

取计算区域为［－0.5，0.5］，初始条件为

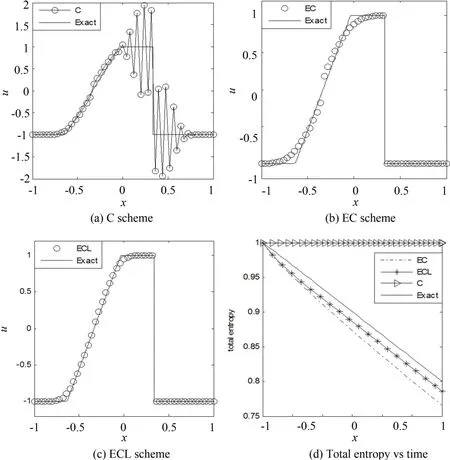
图3 Burgers方程间断初值问题的数值结果Fig.3 Numerical results of discontinuous IVP of Burgers equation（t＝0.3，N＝50）

采用齐次Neumann边界条件，取CFL＝0.3，空间网格数为N＝200，计算到时间t＝0.16．其精确解从左到右依次包括稀疏波、接触间断和激波.采用C、EC2、EC2L格式对密度的计算结果进行比较，见图4（a）－（c）.同样由于C格式缺乏耗散机制而表现出强烈的振荡现象，而其他两种格式的解都没有产生振荡，其中由于EC2格式是一阶精度，在解的间断位置抹平得较为严重，而EC2L格式在解的激波和接触间断处都表现出比较锐利的捕捉效果.图4（d）中三种格式和精确解的总熵－ΔxΣi（ρiSi）随时间变化的比较也可体现，C格式的总熵不变，精确解、EC2和EC2L格式的总熵都有所耗散，当然精确解的熵耗散最少也最合适，EC2的多于EC2L，所以比EC2L抹平得严重.

3.2.2 一维Euler方程Sod激波管问题

取计算区域为［－0.5，0.5］，初始条件为

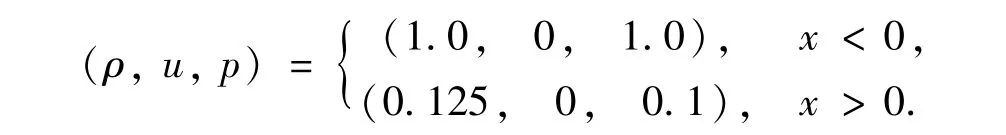
采用齐次Neumann边界条件，取CFL＝0.3，空间网格数为N＝200，计算到时间t＝0.1．精确解包括三部分，分别为稀疏波、接触间断和激波.密度的计算结果如图5（a）－（c）所示，与前述算例一样，熵守恒C格式的解有明显的振荡，EC2格式对解的捕捉有很大的改进，但间断处的抹平现象同样比较严重，而EC2L格式对此进行了良好的改善.图5（d）是各格式总熵变化的比较，与前算例的结论一样：C的总熵不变，精确解的熵耗散最适中，EC2的熵耗散比EC2L的多，且这两者的熵耗散都比精确解的多.

3.2.3 一维Euler方程低密度流问题

在区域［－0.5，0.5］上取初始条件

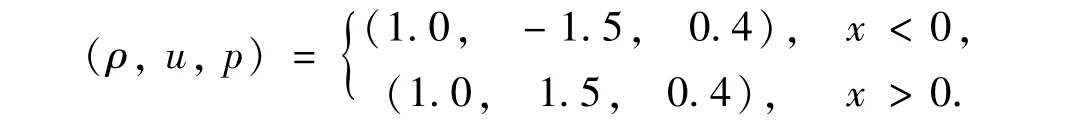
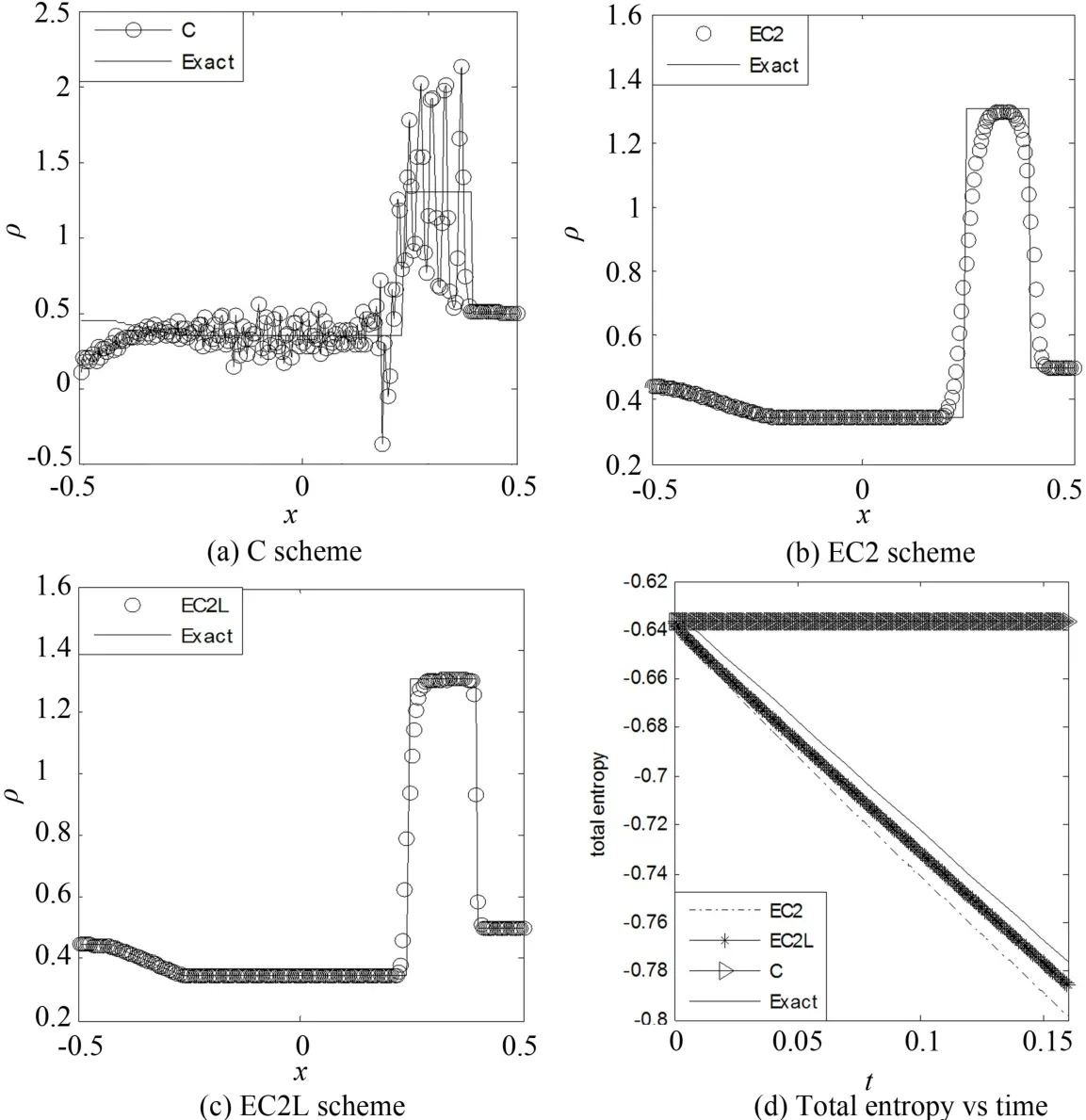
图4 一维Euler方程Lax激波管问题的数值结果Fig.4 Numerical results of 1D Euler equation in Lax shock tube problem（t＝0.16，N＝200）

图5 一维Euler方程Sod激波管问题的数值结果Fig.5 Numerical results of 1D Euler equation in Sod shock tube problem（t＝0.1，N＝200）

采用齐次Neumann边界条件，取CFL＝0.3，空间网格数N＝200，计算到时间t＝0.05．其精确解包括两个强稀疏波和一个平凡的接触间断.解的中间部分压力几乎为0，接近于真空状态，很多数值方法在该位置会出现压力为负的情况，使计算无法进行，如熵守恒格式C计算到第11步时，压力就为负了，图6（a）只给出了第11步的数值结果.而其他两种格式都能使计算顺利完成，且都对解的结构有准确的捕捉，见图6 （b）－（c）.对本算例，同样有EC2L格式的结果优于EC2格式的结果，进一步体现了高分辨率熵相容格式的优点，图6（d）是其总熵关于时间变化的对比，可见C格式前10步的总熵依然没有变化，而EC2L的熵耗散几乎与精确解的完全重合，但如果放大图的比例还是能看出，精确解的熵耗散稍小些，EC格式比起这两者，其耗散就比较多了.

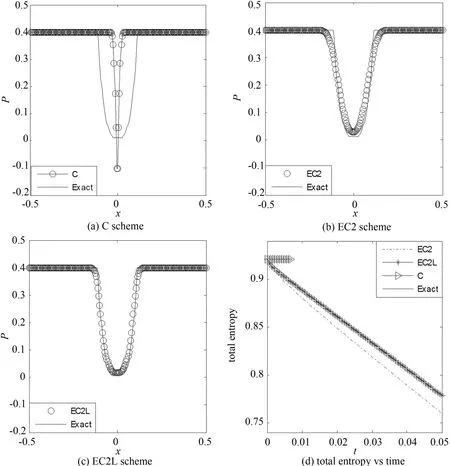
图6 一维Euler方程低密度流问题的数值结果Fig.6 Numerical results of 1D Euler equation in Low density problem（t＝0.05，N＝200）

3.2.4 一维Euler方程强稀疏波问题

在区域［－10，15］上，初始条件为

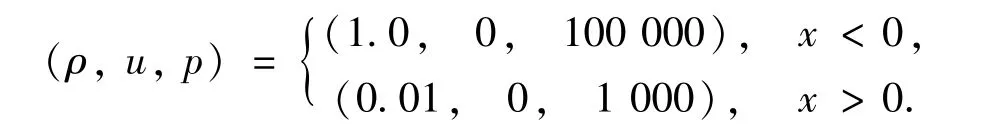
采用齐次Neumann边界条件，取CFL＝0.3，空间网格数为N＝200，计算到时间t＝0.01．其精确解包括稀疏波，接触间断和激波.依然采用上述三种格式，密度的计算结果如图7所示.熵守恒C格式有明显的振荡，EC2和EC2L格式在稀疏波段均有一个平滑的过渡，但在间断处，同3.2.1和3.2.2的算例一样，EC2格式的抹平较严重，而EC2L有很大的改进，充分体现了EC2L格式的优良性.图7（d）显示了各格式对应的总熵关于时间的变化，它们各自耗散的多少说明了与前面几个算例相同的结论：在精确解熵耗散的对比下，熵守恒格式的熵不变；熵相容EC2格式的耗散最多，导致其数值结果在间断处抹平严重；高分辨率熵相容EC2L格式的耗散少且较为适中，表现了锐利的捕捉效果.

3.2.5 一维Euler方程爆炸波问题

在计算区域［－0.5，0.5］上，初始条件为

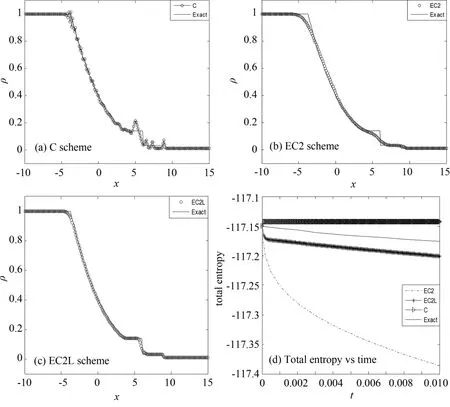
图7 一维Euler方程强稀疏波问题的数值结果Fig.7 Numerical results of 1D Euler equation in strong expansion problem（t＝0.01，N＝200）

采用反射边界条件，取CFL＝0.4，空间网格数为N＝400，计算到时间t＝0.038．由于该问题的初始数据有两次间断，已经无法用经典的精确Riemann求解器计算其精确解，本文采用文献［16］中的WENO-RF－3格式在800个空间网格上的数值解作为精确解，对比EC2和EC2L格式的数值结果，分别见图8（a）和（b），很显然EC2L比EC2有很大的改进，这也进一步说明了EC2L格式具有一定的实用性.

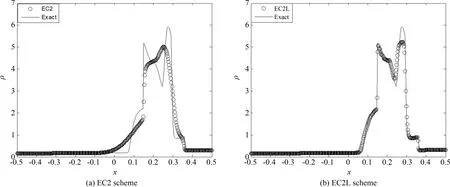
图8 一维Euler方程爆炸波问题的数值结果Fig.8 Numerical results of 1D Euler equation in blast waves problem（t＝0.038，N＝400）

4 结论

通过推广原始的Superbee限制器得到一类广泛的GSbee类限制器，随着α，β，γ的连续变化，这类限制器覆盖了整个二阶TVD区域；取α＝1，β＝2，γ＝1构造出S-M限制器；然后根据传统的构造二阶TVD格式的思想，利用此限制器构造得到高分辨率熵相容格式，同时对Euler方程的熵相容格式的几个参数做了简单的调整，使其对接触间断的捕捉更精确；在本文的第3节通过几个数值算例将所得高分辨率熵相容格式的数值结果与熵相容格式和熵守恒格式的数值结果比较分析，从直观上说明了S-M限制器的高分辨率熵相容格式的合理性和优良性.另外需要说明的是

1）本文只是在熵守恒和熵相容格式的基础上，采用S-M限制器构造高分辨率格式，至于S-M限制器是否适合于其他经典格式的高分辨率格式构造，还有待进一步研究；

2）由于熵相容EC2格式对不同的问题需要调整一些参数的大小［8］，如αmin、αmax、β1和β2，所以得到的相应的高分辨率熵相容格式如果要对所有的问题（包括定常［8］和非定常问题）都适用，同样需要调整各个参数的大小.为了进一步提高该格式的实用性，有待下一步从Euler方程熵相容格式本身的构造上进行改进，如修正其格式中的稳定项和熵增项；

3）最后是关于熵相容格式和高分辨率熵相容格式向高维问题的推广使用，由于高维情形下每个点的信息具有无限多的传播方向，为了更准确地反映多维效应的影响，我们将在未来的工作中将本文的格式与旋转Riemann求解器结合，实现对高维问题的计算研究.

［1］Lax P D.Weak solutions of non-linear hyperbolic equations and their numerical computations［J］.Comm Pure Appl Math，1954，7（1）：159－193.

［2］Lax P D.Hyperbolic systems of conservation laws and the mathematical theory of shock waves［C］∥11th of SIAM Regional Conferences Lectures in Applied Mathematics.Philadelphia：Society for Industrial and Applied Mathematics，1973：1－48.

［3］Tadmor E.The numerical viscosity of entropy stable schemes for systems of conservation laws［J］.Math Comp，1987，49 （179）：91－103.

［4］Tadmor E.Entropy stability theory for difference approximations of nonlinear conservation laws and related time-dependent problems［J］.Acta Numer，2003，12（1）：451－512.

［5］Tadmor E，Zhong W.Entropy stable approximations of Navier-Stokes equations with no artificial numerical viscosity［J］.J Hyperbolic Differ Equ，2006，3（3）：529－559.

［6］Tadmor E，Zhong W.Energy preserving and stable approximations for the two-dimensional shallow water equations［M］∥Mathematics and computation，a contemporary view，Proc of the third Abel symposium.Berlin Heidelberg：Springer，2008：67 －94.

［7］Roe P L.Entropy conservative schemes for Euler equations［R］.Talk at HYP 2006，Lyon，France.2006.

［8］Ismail F，Roe P L.Affordable，entropy-consistent Euler flux functions II：Entropy production at shocks［J］.J Comput Phys，2009，228（15）：5410－5436.

［9］Toro E F.Riemann solvers and numerical methods for fluid dynamics：A practical introduction［M］.Springer，1997.

［10］Thomas J W.Numerical partial differential equations：Finite difference methods［M］.Springer，1995.

［11］Gottlieb S，Shu C W，Tadmor E.High order time discretizations with strong stability properties［J］.SIAM Review，2001，43 （1）：89－112.

［12］Roe P L.Some contributions to the modeling of discontinuous flows［C］∥Large-scale computations in fluid mechanics. Providence，RI：American Mathematical Society，1985：163－193.

［13］Yee H C.Construction of explicit and implicit symmetric TVD schemes and their applications［J］.J Comput Phys，1987，68 （1）：151－179.

［14］Sweby P K.High resolution schemes using flux limiters for hyperbolic conservation Laws［J］.SIAM J Num Analy，1984，21 （5）：995－1011.

［15］Sweby P K，Baines M J.On convergence of Roe's scheme for the general non-linear scalar wave equation［J］.J Comput Phys，1984，56（1）：135－148.

［16］Jiang G S，Shu C W.Efficient implementation of weighted ENO schemes［J］.J Comput Phys，1996，126（1）：202－228.

High Resolution Entropy Consistent Schemes for Hyperbolic Conservation Laws

REN Jiong1，2，FENG Jianhu1，LIU Youqiong1，LIANG Nan1

（1．College of Science，Chang'an University，Xi'an 710064，China；2．Department of Fluid Dynamics，College of Aeronautics，Northwestern Polytechnical University，Xi'an 710072，China）

To improve accuracy of entropy consistent schemes，we proposed high resolution entropy consistent schemes by inserting a new flux limiter into entropy consistent schemes.It uses limiter mechanism to construct high resolution schemes.In constructing high resolution entropy consistent schemes of Euler equations，we improve resolution of contact discontinuity by adjusting parameters of corresponding entropy consistent schemes.Several numerical experiments illustrate robustness and essentially non-oscillations of the schemes.

hyperbolic conservation laws；entropy consistent scheme；limiter；high resolution

date：2013－07－17；Revised date：2013－12－31

O354；O241.82

A

2013－07－17；

2013－12－31

国家自然科学基金（11171043）和长安大学中央高校基本科研业务费（CHD2102TD015）资助项目

任炯（1985－），女，山西吕梁，硕士生，从事科学与工程中的高性能计算技术研究，E-mail：rensj6962＠163.com

*通讯作者

1001-246X（2014）05-0539-13