混凝土KR阻力曲线的实用解析方法
2014-06-09莫卓凯吴智敏曲秀华
莫卓凯,董 伟,吴智敏,曲秀华
(大连理工大学 海岸和近海工程国家重点实验室,辽宁 大连 116024)
混凝土KR阻力曲线的实用解析方法
莫卓凯,董 伟,吴智敏,曲秀华
(大连理工大学 海岸和近海工程国家重点实验室,辽宁 大连 116024)
根据混凝土Ⅰ型裂缝扩展准则,提出了新的KR阻力曲线及计算新方法。该KR阻力曲线认为,裂缝的扩展阻力由混凝土材料起裂断裂韧度KiniIc和黏聚力提供的阻力组成并等于裂缝扩展的驱动力。采用该方法,只需给出混凝土的起裂断裂韧度KiniIc,弹性模量E,抗拉强度ft和断裂能GF便可计算混凝土的KR阻力曲线,而无需测定试件的荷载-裂缝口张开位移(P-CMOD)全曲线。在此基础上,研究了混凝土三点弯曲梁试件强度等级从C20到C120的KR阻力曲线,计算了强度相同初始缝高比不同以及初始缝高比相同而试件高度不同的混凝土KR阻力曲线,并探讨了各种情况下的断裂过程区长度以及黏聚力分布。研究结果表明:混凝土强度等级提高,KR阻力曲线上升,但其上升幅值逐渐减小,强度等级在C60以后,其上升幅值趋于稳定;混凝土的KR阻力曲线存在一定的尺寸效应,当韧带长度足够大时,KR阻力先增大,而后趋于稳定;混凝土强度等级提高,最大完整断裂过程区长度减小;试件的尺寸对断裂过程区长度也有着较大影响。
混凝土;KR阻力曲线;断裂过程区;裂缝;黏聚力;起裂断裂韧度
混凝土是一种多相复合材料,其破坏和断裂机理非常复杂。很多大型混凝土结构如混凝土坝等的破坏都是由裂缝引起的,所以研究混凝土结构的裂缝扩展KR阻力曲线有着重要的意义。为了描述裂缝在混凝土材料中的扩展,许多学者开始研究以应力强度因子形式描述的裂缝扩展阻力及其相关特征。

很多学者还对影响混凝土KR阻力曲线的因素进行了研究。徐世烺和H.W.Reinhardt[5]的研究结果表明,KR阻力曲线与材料本身的特性有关,与试件的尺寸无关。S.Kumar和S.V.Barai[11]采用三点弯曲梁试件和紧凑拉伸试件研究了试件型式和试件尺寸对KR阻力曲线的影响,研究发现KR阻力曲线与试件的型式无关,但与试件尺寸相关。徐锋等[12]根据试验测得的P-CMOD曲线,研究了断裂过程区长度对KR阻力曲线的影响,发现KR阻力随着裂缝扩展而增大,但达到完整断裂过程区长度后,会趋于恒定值。
尽管国内外对混凝土的KR阻力曲线进行了大量研究,但仍有以下工作要做:①没有考虑混凝土裂缝扩展中断裂过程区的变化;②P-CMOD曲线与断裂能的取值相互独立,与实际情况相矛盾;③缺乏对高强混凝土KR阻力曲线方面的研究;④关于试件尺寸对KR阻力曲线是否存在影响,仍没有一致的结论。
针对上述问题,本文基于混凝土裂缝扩展准则,采用解析方法,研究混凝土三点弯曲梁试件强度等级从C20到C120的KR阻力曲线,研究强度相同初始缝高比不同以及初始缝高比相同而试件高度不同的混凝土KR阻力曲线并讨论其尺寸效应,还对不同情况下的断裂过程区长度的变化规律进行研究。
1 基于裂缝扩展准则的KR阻力曲线


式中:KIP为由外荷载P引起的裂缝尖端应力强度因子;KIσ为由黏聚力σ(W)引起的裂缝尖端应力强度因子。



而在裂缝扩展过程中,裂缝扩展准则的表达式为[9]:
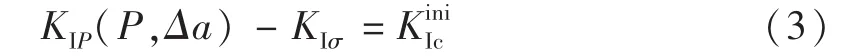
对比式(2)与式(3),可以得到:
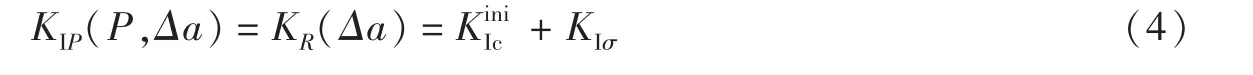
式中:Δa为对应于P时的裂缝扩展量。
根据裂缝扩展准则,外力为裂缝扩展的驱动力,它克服阻力使裂缝扩展。无论荷载处于上升段还是下降段,都有与其相对应的裂缝扩展量Δa,该驱动力克服阻力使裂缝继续扩展,即阻力与驱动力是相同的。将同一构件不同裂缝长度及与其相对应的驱动力所产生的应力强度因子建立函数关系,即可计算混凝土的KR阻力曲线。
2 KR阻力曲线的实用解析方法
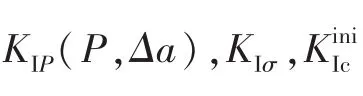
本文采用标准三点弯曲梁试件(见图1),外力产生的应力强度因子KIP(P,Δa)可以由H.Tada等[14]提出的表达式求得:

式中:a为有效裂缝长度;D为试件高度;B为试件厚度;S为试件跨度。
根据文献[15],由黏聚力产生的应力强度因子KIσ为:

式中:σ(x)为x处的黏聚应力;a0为初始裂缝长度。
根据P.E.Peterson[16]建议的双线性软化本构曲线(如图2所示),σ(x)的表达式如下:
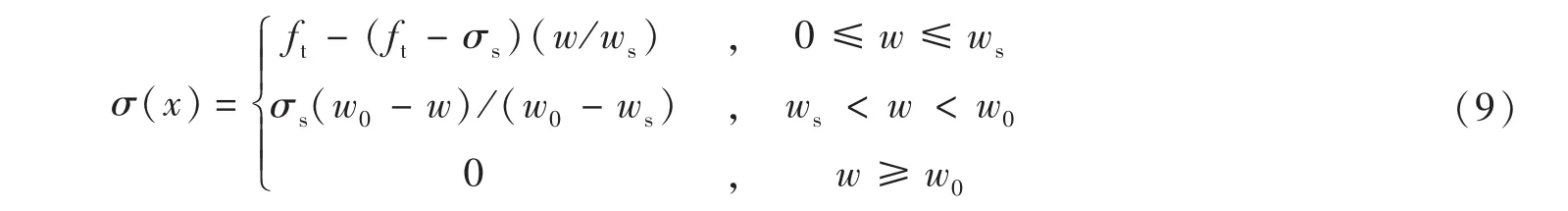
式中:ft为混凝土的抗拉强度;W为裂缝张开位移。

图1 混凝土三点弯曲梁Fig.1 Three-point bending beam
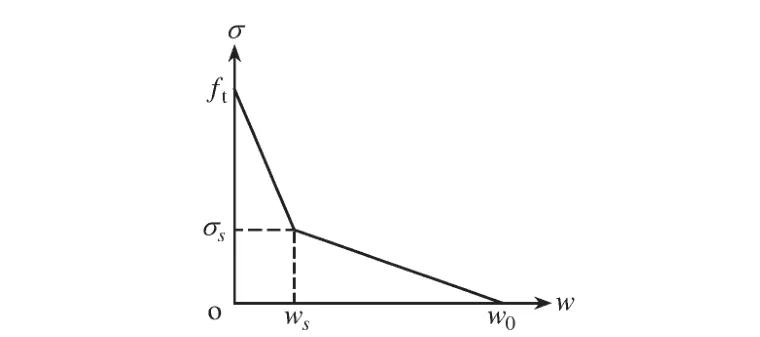
图2 双线性软化本构曲线Fig.2 Curve of bilinear softening traction-separation law
σs,Ws与W0的值可以分别由以下式求出,GF为混凝土的断裂能:

有效裂缝长度扩展到a时,x处对应的裂缝张开位移W可用文献[15]中的公式求得:
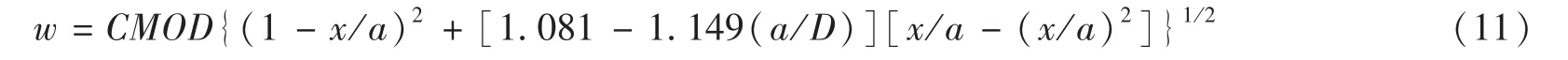
而CMOD的值由H.Tada[14]提出的公式求得:
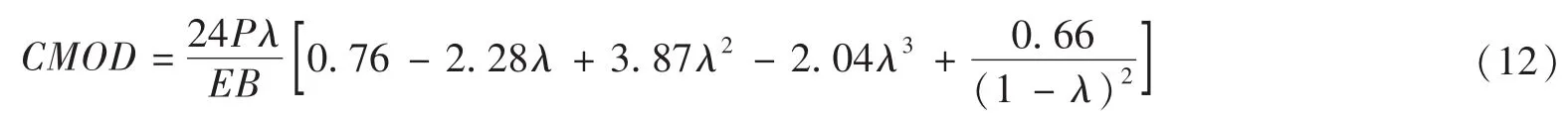
式中:E为混凝土的弹性模量;λ=(a-H0)/(D+H0);H0为放置夹式引申仪的刀片边缘厚度。综上可得,KIσ可以由式(7)~(12)求得。
3 试验及结果分析
3.1 材料参数的选取
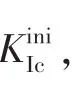
根据欧洲混凝土模式规范CEB-FIB Model Code 2010[17],混凝土的弹性模量E和断裂能GF可以通过下式求得:


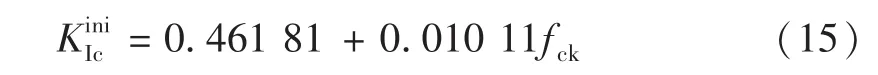
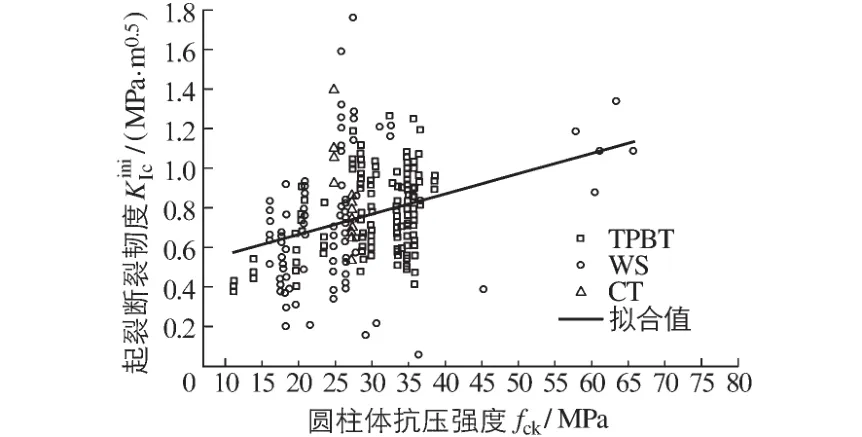
图3 起裂断裂韧度分布Fig.3 Initial fracture toughness for different compressive strengths
利用以上材料参数的公式,得到所需的材料参数列于表1。采用上节的解析方法,对3组不同的混凝土试件进行KR阻力曲线计算。

表1 材料参数Tab.1 The material parameters of concrete
这3组试件分别为:
第1组,同一尺寸不同混凝土强度的试件。强度等级分别为C20,C40,C60,C80,C100和C120的混凝土三点弯曲梁试件。试件尺寸相同,跨度S为800 mm,高度D为200 mm,厚度B为100 mm,初始缝高比a0/D都为0.4。
第2组,同一强度不同缝高比的试件。强度等级均为C40的混凝土三点弯曲梁试件,试件尺寸同第1组一致。而初始缝高比a0/D分别为0.05,0.1,0.2,0.3,0.4,0.5,0.6,0.7和0.8。
第3组,同一缝高比不同试件高度的试件。强度等级均为C40的混凝土三点弯曲梁试件,试件初始缝高比a0/D为0.4,试件厚度B为100 mm。试件高度D分别为200,400,600,800,1 000,1 500和2 000,试件的跨高比S/D都为4。
3.2 KR阻力曲线的计算结果分析
利用上述解析方法,输入每组所需的材料参数,即可得到每组KR阻力曲线。

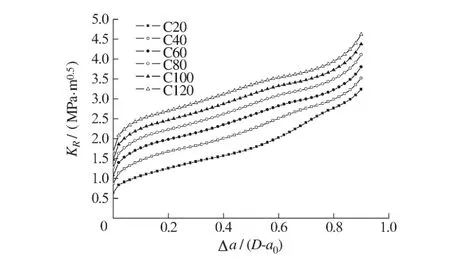
图4 KR阻力曲线随强度等级的变化Fig.4 KRcurves for different strength grades
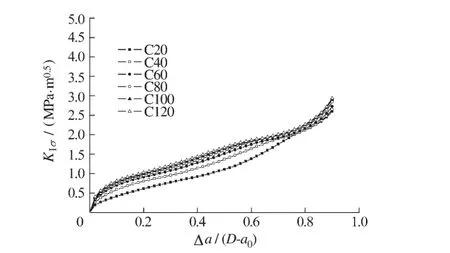
图5 KIσ曲线随强度等级的变化Fig.5 KIσcurves for different strength grades
将第2组的KR阻力曲线的计算结果绘于图6中。从图6可知,试件的初始缝高比对混凝土KR阻力曲线有一定的影响,不同试件初始缝高比的KR阻力曲线在Δa/(D-a0)为0.6之前,随初始缝高比的增大,KR阻力曲线减小,在Δa/(D-a0)为0.6之后,随初始缝高比的增大,KR阻力曲线增大。
将第3组的KR阻力曲线的计算结果绘于图7中。从图7可知,试件高度对混凝土KR阻力曲线有一定的影响,不同试件高度的KR阻力曲线在Δa/(D-a0)为0.4之前,随试件高度的增大,KR阻力曲线增大,在Δa/(D-a0)为0.6之后,随试件高度的增大,KR阻力曲线减小。
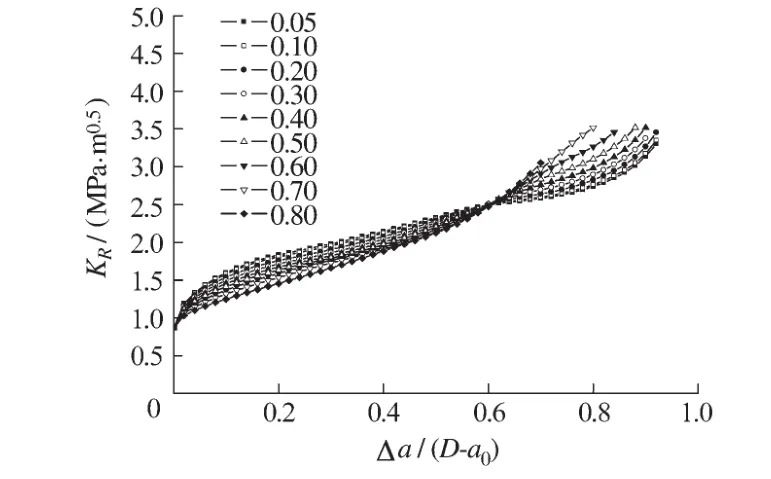
图6 KR阻力曲线随试件初始缝高比的变化Fig.6 KRcurves for different initial crack length/depth ratios
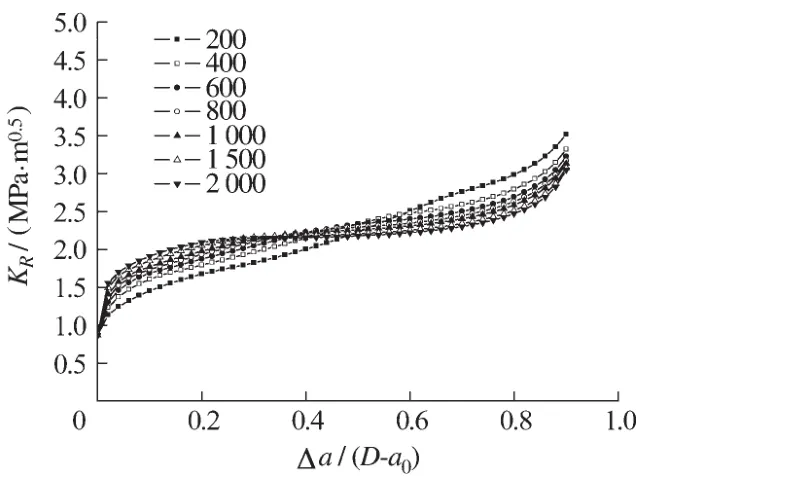
图7 KR阻力曲线随试件高度的变化Fig.7 KRcurves for different depths
总结第2和第3组的计算结果,可得出一个结论:混凝土的KR阻力曲线存在一定的尺寸效应。观察图6与图7,发现试件的韧带长度越长,其KR阻力曲线越平缓。强度等级为C40,初始缝高比a0为0.2,试件高度D为2 000 mm的混凝土试件的KR阻力曲线如图8所示。从图8可知,当韧带长度足够长时,KR阻力先增大,而后趋于稳定。
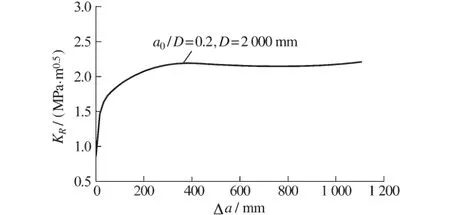
图8 韧带足够长时的KR阻力曲线Fig.8 KRcurve for infinite ligament length
3.3 混凝土FPZ(断裂过程区)长度的结果分析
断裂过程区(fracture process zone,简写为FPZ)是裂缝扩展过程中宏观裂缝前端的微裂缝区,断裂过程区内分布着阻碍裂缝扩展的黏聚力,FPZ的存在是断裂能和断裂韧度等断裂参数具有尺寸效应和边界效应的主要原因。完整FPZ长度是指黏聚力σ从0所对应的位置到ft所对应的位置之间的长度,FPZ长度的计算就是用有效裂缝长度a减去W0所对应位置的裂缝长度,通过上述解析方法可以求得。
将3组试件的计算结果分别绘于图9中,可知:断裂过程区长度随着裂缝扩展而发生变化,先随着有效裂缝长度的增加而增加,当裂缝尖端张开位移为W0时,达到完整断裂过程区长度,然后开始减小。由图9 (a)可知,混凝土强度提高,最大完整断裂过程区长度减小,达到完整断裂过程区时的裂缝扩展长度与韧带长度的比值减小;由图9(b)可知,试件的初始缝高比增大,最大完整断裂过程区长度减小,达到最大完整断裂过程区时的裂缝扩展长度与韧带长度的比值增大;由图9(c)可知,随试件高度的增加,最大完整断裂过程区长度增大,达到最大完整断裂过程区时的裂缝扩展长度与韧带长度的比值减小。
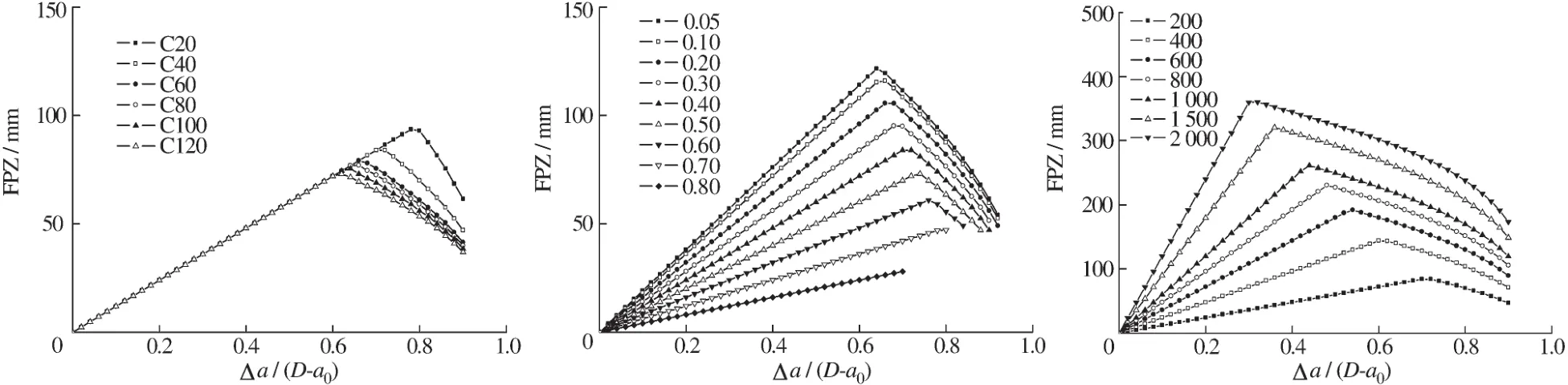
图9 FPZ长度随强度等级、试件初始缝高比及试件高度的变化Fig.9 FPZ lengths for different strength grades,different initial crack length/depth ratios and different depths
裂缝扩展至有效裂缝长度a,会有其对应的FPZ长度与黏聚力分布,通过图2即可确定。选取第2组中初始缝高比为0.05,0.4,0.8的试件,分别绘制FPZ长度与黏聚力分布的变化(见图10)。图10(a)与图10 (b)均分为4个阶段:第1阶段表示的是裂缝开始失稳扩展的时刻(图(a1)和(b1));第2阶段表示的是起始裂缝尖端的黏聚力减小至0的时刻(图(a2)和(b2)),即达到最大完整断裂过程区长度的时刻;第3阶段表示达到最大完整断裂过程区长度后,裂缝尖端不受力,黏聚力为0的点后移,FPZ长度开始减小的时刻(图(a3)和(b3));第4附件表示的是裂缝扩展到接近试件边界处的时刻(图(a4)和(b4))。由于初始缝高比为0.8的试件,韧带长度过短,不能扩展至完整断裂过程区,因此只选取了3个阶段:图(c1)表示的是裂缝开始失稳扩展的时刻;图(c2)表示的是有效裂缝长度a扩展至0.92D的时刻;图(c3)表示的是裂缝扩展到接近试件边界处的时刻。

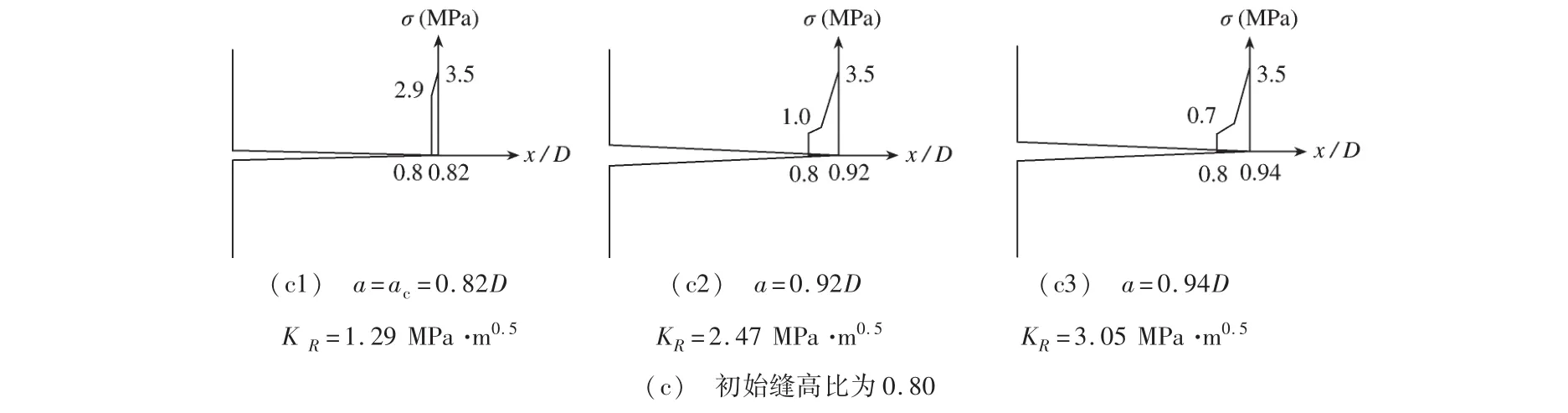
图10 不同初始缝高比试件的FPZ长度与黏聚力分布的变化Fig.10 Variation of FPZ length and cohesive stress distribution within the FPZ for specimen with different ratios of a0/D
4 结 语
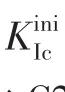
(1)混凝土强度等级提高,KR阻力曲线上升,但其上升幅值逐渐减小,强度等级达到C60以后,其上升幅值趋于稳定。
(2)混凝土的KR阻力曲线存在一定的尺寸效应。不同初始缝高比的KR阻力曲线在Δa/(D-a0)为0.6之前,随初始缝高比的增大,KR阻力曲线减小,在Δa/(D-a0)为0.6之后,随初始缝高比增大,KR阻力曲线增大;不同试件高度的KR阻力曲线在Δa/(D-a0)为0.4之前,随试件高度的增大,KR阻力曲线增大,在Δa/(D-a0)为0.6之后,随试件高度的增大,KR阻力曲线减小。
(3)当韧带长度足够长时,KR阻力先增大,而后趋于一稳定值。
(4)混凝土强度等级提高,最大完整断裂过程区长度减小,达到完整断裂过程区时的裂缝扩展长度与韧带长度的比值减小。
(5)试件的初始缝高比增大,最大完整断裂过程区长度减小,达到最大完整断裂过程区时的裂缝扩展长度与韧带长度的比值增大;随试件高度的增加,最大完整断裂过程区长度增大,达到最大完整断裂过程区时的裂缝扩展长度与韧带长度的比值减小。
[1]ASTM-STP 527,Fracture toughness evaluation by R-Curve methods[S].
[2]LENAIN J C,BUNSELL A R.The resistance to crack growth of asbestos cement[J].Journal of Materials Science,1979,14 (2):321-332.
[3]BAŽANT Z P,JIRASEK M.R-curve modeling of rate and size effects in quasibrittle fracture[J].International Journal of Fracture,1993,62:355-373.
[4]REINHARDT H W,XU Shi-lang.Crack extension resistance based on the cohesive force in concrete[J].Engineering Fracture Mechanics,1999,64(5):563-587.
[5]HILLERBORG A,MODEER M,PETERSSON P E.Analysis of crack formation and crack growth in concrete by means of fracture mechanics and finite elements[J].Cement and Concrete Research,1976,6:773-782.
[6]丁生根.基于虚拟裂缝闭合力的混凝土双K断裂参数及KR阻力曲线[D].大连:大连理工大学,2001.(DING Shenggen.Research on concrete′s fracture double-K parameters and the KR-curve[D].Dalian:Dalian University of Technology,2001.(in Chinese))
[7]徐世烺,吴智敏,丁生根.砼双K断裂参数的实用解析方法[J].工程力学,2003,20(3):54-61.(XU Shi-lang,WU Zhi-min,DING Sheng-gen.A practical analytical approach to the determination of double-K fracture parameter of concrete[J]. Engineering Mechanics,2003,20(3):54-61.(in Chinese))
[8] KUMAR S,BARAI S V.Weight function approach for determining crack extension resistance based on the cohesive stress distribution in concrete[J].Engineering Fracture Mechanics,2009,76(8):1131-1148.
[9]董伟,何化南,吴智敏,等.基于裂缝扩展准则的KR阻力曲线研究[J].工程力学,2011,28(7):13-19.(DONG Wei,HE Hua-nan,WU Zhi-min,et al.A study of KR-curve based on crack propagation criterion in concrete[J].Engineering Mechanics,2011,28(7):13-19.(in Chinese))
[10]吴智敏,董伟.混凝土Ⅰ型裂缝扩展准则及裂缝扩展全过程的数值模拟[J].水利学报,2007,38(12):1453-1459. (WU Zhi-min,DONG Wei.Mode I crack propagation criterion of concrete and numerical simulation of complete process of cracking[J].Journal of Hydraulic Engineering,2007,38(12):1453-1459.(in Chinese))
[11]KUMAR S,BARAI S V.Influence of specimen geometry and size-effect on the KR-curve based on the cohesive stress in concrete[J].International Journal of Fracture,2008,152(2):127-148.
[12]XU F,WU Z M,ZHENG J J,et al.Crack extension resistance curve of concrete considering variation of FPZ length[J]. Journal of Materials in Civil Engineering,ASCE,2011,23(5):703-710.
[13]XU S,REINHARDT H W.Determination of double-K criterion for crack propagation in quasi-brittle fracture,PartⅡ:Analytical evaluating and practical measuring methods for three-point bending notched beams[J].International Journal of Fracture,1999,98(2):151-177.
[14]TADA H,PARIS P C,IRWIN G R.The stress analysis of cracks handbook[M].ASME,2000.
[15]JENQ Y S,SHAH S P.A fracture toughness criterion for concrete[J].Engineering Fracture Mechanics,1985,21(5):1055-1069.
[16]PETERSSON P E.Crack growth and development of fracture zones in plain concrete and similar materials[R].Report TVBM-1006.Sweden:Division of Building Materials,Lund Institute of Technology,1981.
[17]CEB-FIP:Model Code 2010-First complete draft,Volume 1[S].2010.
[18]XU S,REINHARDT H W.A simplified method for determining double-K fracture parameters for three-point bending tests[J]. International Journal of Fracture,2000,104(2):181-209.
[19]XU S,REINHARDT H W.Determination of double-K criterion for crack propagation in quasi-brittle fracture,PartⅢ:Compact tension specimens and wedge splitting specimens[J].International Journal of Fracture,1999,98(2):179-193.
[20]KUMAR S,BARAI S V.Determining double-K fracture parameters of concrete for compact tension and wedge splitting tests using weight function[J].Engineering Fracture Mechanics,2009,76(7):935-948.
[21]荣华,董伟,吴智敏,等.大初始缝高比混凝土试件双K断裂参数的试验研究[J].工程力学,2012,29(1):162-167. (RONG Hua,DONG Wei,WU Zhi-min,et al.Experimental investigation on double-K fracture parameter for large initial crack-depth ratio in concrete[J].Engineering Mechanics,2012,29(1):162-167.(in Chinese))
[22]高淑玲,王玲,徐世烺.高强混凝土双K断裂参数测试及计算方法[J].水利水电科技进展,2010,30(3):28-31. (GAO Shu-ling,WANG Ling,XU Shi-lang.Tests and methods of double-K fracture parameters for high strength concrete[J]. Advances in Science and Technology of Water Resources,2010,30(3):28-31.(in Chinese))
[23]吴智敏,徐世烺,刘佳毅.光弹贴片法研究混凝土裂缝扩展过程及双K断裂参数的尺寸效应[J].水利学报,2001,(4):34-39.(WU Zhi-min,XU Shi-lang,Liu Jia-yi.Study on crack propagation process of concrete and size effect of double-K fracture parameter by means of photoelastic coatings[J].Journal of Hydraulic Engineering,2001,(4):34-39.(in Chinese))
[24]刘红梁,宋罕宇.高强混凝土立方体强度变异系数的商榷[J].哈尔滨商业大学学报:自然科学版,2004,20(5):604-607.(LIU Hong-liang,SONG Han-yu.Discuss on variation factor of high-strength concrete cube strength[J].Journal of Harbin University of Commerce(Natural Science Edition),2004,20(5):604-607.(in Chinese))
A practical analytical approach to determine KR-curves of concrete
MO Zhuo-kai,DONG Wei,WU Zhi-min,QU Xiu-hua
(State Key Laboratory of Coastal and Offshore Engineering,Dalian Uniυersity of Technology,Dalian 116024,China)
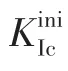
concrete;KRextension resistance curve;fracture process zone(FPZ);crack;cohesive force;fracture toughness of concrete cracking
TV431 文献标心码:A
1009-640X(2014)03-0009-09
2013-11-05
国家自然科学基金资助项目(51109026)
莫卓凯(1989-),女,湖南益阳人,硕士研究生,主要从事混凝土断裂机理研究。E-mail:mozhuok@163.com
