潮间带地区跨海大桥设计流速计算分析

翟剑峰，东培华，熊 伟，董 佳

(1.江苏省交通规划设计院股份有限公司，江苏 南京 210005；2.江苏省水运工程技术研究中心，江苏 南京 211100）

潮间带地区跨海大桥设计流速计算分析

翟剑峰1，2，东培华1，2，熊 伟1，2，董 佳1，2

(1.江苏省交通规划设计院股份有限公司，江苏 南京 210005；2.江苏省水运工程技术研究中心，江苏 南京 211100）

在大桥设计中设计流速是一项重要参数，其预测的准确性事关桥梁的安全施工和安全运行。通常采用实测资料分析推求或数学模型计算两种预测方法。为确保跨海大桥施工和运行的安全性，需要对设计流速进行准确预测。利用数学模型预测工程区域可能最大流速是一种有效的方法。应用基于有限体积法的二维浅水方程和干湿边界处理技术，建立了工程海区的潮流数学模型，并结合实测资料进行验证。在此基础上，考虑了有无风浪作用的不同工况组合，计算分析得到潮间带地区大桥工程位置在不同重现期的设计流速，为桥梁设计和相关物理模型试验研究提供重要参数。计算分析结果表明，风浪对潮间带地区的流场影响较大，桥梁设计流速计算时应充分考虑这一关键因素，以此保证桥梁施工和运行安全。

跨海大桥；潮间带；干湿边界；重现期；数值模拟；风浪作用

连云港市海滨大道建设沿着连云港市东海岸线贯穿南北，北起赣榆绣针河，南至灌云县灌河口，全长约120 km。连云港跨海大桥起于高公岛渔港，终于烧香河新闸，是连云港市海滨大道的一个重要组成部分，成为连接海湾南北的重要通道。

设计流速是桥梁设计中的一项重要参数，其预测的准确性关系到桥梁施工和运行的安全性。设计流速一般有如下两种预测方法：一是根据实测资料，利用相关法推求［1-2］；二是利用数学模型来计算［3］。由于工程位置的水深较小，附近实测潮位流速资料很少，因此，很难利用实测资料建立相关关系式来推求设计流速。许雪峰等［4］根据杭州湾滩涂上的实测潮流资料分析后指出，漫滩流的流速明显小于前沿深水区域，且漫滩区潮流漫滩过程(涨潮）和露滩过程(落潮）的时间并不对称。而本大桥工程位于近岸潮滩地区，在一个完整潮的周期中，大部分区域处于淹没和干出交替变化状态，且风吹流、风增水等现象比较明显，波浪辐射应力对流场也有着关键影响［5］。综合以上因素，本工程设计流速采用数学模型的方法来进行计算。从考虑有无风浪的角度出发，分别计算大桥工程位置在不同重现期的最大流速值。

1 数学模型及计算方法

1.1 基本方程

MIKE 21为海岸和近海工程应用提供了完备有效的设计环境，已被广泛应用于河口、海岸及海洋水流、波浪、泥沙等方面的模拟。本次工程所在区域潮流场的计算采用MIKE21中的HD模块［6-7］。模型基于二维平面不可压缩雷诺(Reynolds）平均Navier-Stokes浅水方程建立，对水平动量方程和连续性方程在h=η+d范围内进行积分后可得到下列二维深度平均浅水方程：

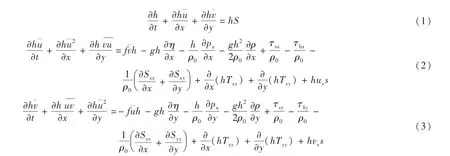
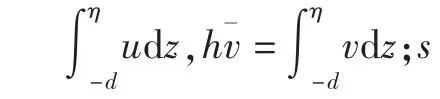
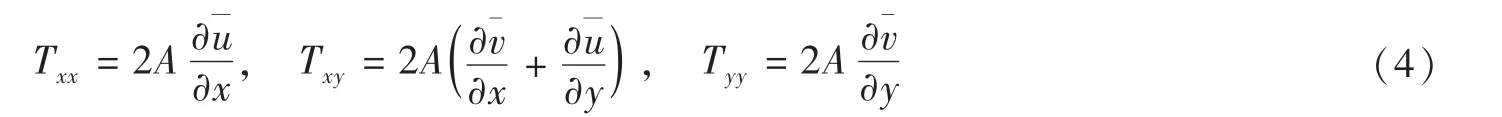
1.2 设计流速计算方法

潮差是表示潮汐动力强弱的因素，也是天文潮、风暴潮等多种动力因子综合作用的结果。但本工程区域由于实测的潮位、潮流资料很少，不可能利用潮流资料来推算不同重现期下的设计流速［8］。另外，由于大桥工程位于近岸地区，风浪对工程区域的流场影响较大，这一因素不容忽视。因此，本次设计流速的计算利用潮流数学模型和潮差来间接计算不同重现期下的设计流速，具体步骤如下：(1）建立并验证平面二维潮流数学模型；(2）高公岛离工程区域最近，利用高公岛在不同重现期下的最大潮差和正常天气下的潮位过程，构造不同重现期下模型边界的潮位过程；(3）根据构造的边界潮位过程，确定不同的工况组合(考虑有无风浪），计算得到大桥工程位置在不同重现期下的最大流速和平均流速。

2 模型的建立与验证

图1 模型计算网格Fig.1 Calculation grids of a tidal current model

2.1 模型计算范围

本次数学模型计算域沿岸方向长约73 km，垂直于岸方向上宽度约46 km，计算域面积约为3 358 km2。为了更准确地拟合岸线，计算网格采用非结构化的三角形网格。在大桥所在位置，网格进行局部加密处理，以保证工程及其附近区域的流场模拟精度，其他地区网格则随距离大桥的远近而自然疏密过度。模型的最小网格尺度为10 m，最大网格尺度为2 000 m，网格布置如图1所示。

2.2 模型参数设置

模型计算的高程基准统一为连云港理论最低潮面，比国家85高程面低270.1 cm。在该潮流数学模型中，通过曼宁系数M值来实现对海底摩阻的模拟。在本次数值模拟中，M的取值范围为45～55。

2.3 模型边界设置

在本次采用的潮流数学模型中，需给定2种边界条件，即闭边界条件和开边界条件：(1）开边界条件，即水域边界条件，可以给定水位或流速，对于本次数值模拟方案，计算域内有2个开边界，3个控制点；(2）闭边界条件，即水陆交界条件，在该边界上，水质点的法向流速为0。

2.4 模型验证

潮流数学模型采用2009年实测潮位、流速资料进行验证，计算时长约为3 d，包含一个完整的大潮过程。潮位、流速实测点位置分布如图2所示。计算得到的潮位验证和流速流向验证如图3和4所示。从验证结果来看，本次计算模拟的潮位验证较好，3#测点流速流向验证较好；1#、2#测点的流向验证较好，但流速值存在些许偏差，可能是由于该点位于徐圩航道工程附近的缘故。模拟的潮流场基本反映了该区域的潮流涨落特征，工程区域及其附近海域的潮流带有典型的旋转流性质，并在近岸地区存在一定的往复流特性。本次计算结果与各测点的潮位、流速过程吻合较好，表明本文建立的数学模型可用于跨海大桥设计流速的计算分析。

图2 潮位、流速实测点位置分布Fig.2 Measuring points of tide level and currents

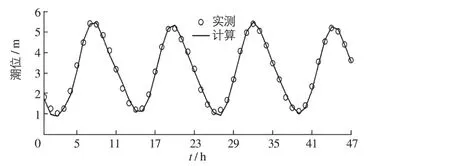
图3 2#测点潮位验证Fig.3 Verification of tide level for 2#measuring point

图4 1#，2#和3#测点流速流向验证Fig.4 Verification of velocity and direction of current for 1#，2#and 3#measuring points

3 设计流速计算

3.1 桥位计算点布置

由于跨海大桥纵向跨越海湾，而海湾南北的水深地形存在较大差异，本次设计流速的计算共取了15个计算点，其中1#～14#沿跨海大桥中心线位置从北到南等间距布置，15#点位跨海大桥的主桥墩位置，1#～15#点的相对位置如图5所示。

3.2 计算工况选取

考虑到风浪对工程区域流场的影响，在本次数值模拟计算中考虑E向、ENE向和NE向3种不利风向、相应的风生浪，按照有无风浪作用的不同条件组合，总共考虑12种计算工况，如表1所示。3种不利风向下的波浪及波浪辐射应力由MIKE21 SW波浪模型［9］计算得到。300年一遇、100年一遇、50年一遇E向风速分别为36.14，32.48和29.92 m/s；在相同重现期下，NE向和ENE向风速相同，其300年一遇、100年一遇、50年一遇风速值分别为33.89，30.75和29.0 m/s。

图5 桥位计算点相对位置Fig.5 Relative positions of calculated points

3.3 设计流速计算

根据大桥工程区域附近的水文测验资料［10］显示，在正常天气情况下，该地区的流速特征表现为离岸远、水深大的区域平均流速大，离岸近、水深小的区域平均流速小，且工程区域邻近海域内的流速普遍较小，靠近海岸地区的平均流速不足0.30 m/s。由于大桥工程位于潮间带地区，本次模型计算的正常天气条件下的流速也都较小，与实测情况相符。

本次研究计算了正常天气条件时，不同重现期下1#～15#计算点的最大流速比值，并将其与海港水文规范中按潮差比计算的最大流速值进行比较，如表2所示。表2中，Uc为常风天最大流速计算值，Um为模型最大流速计算值，Us为按规范计算最大流速计算值。从表2可见，模型计算得到的最大流速值与按照海港水文规范中利用潮差比计算的最大流速值基本相符，其差别在±5%以内，表明模型计算的准确度较好。

表2 无风浪工况时不同重现期下的流速比较Tab.2 Comparison of current velocity without wave under different return periods (m·s-1）

连云港站与高公岛站的同期潮位潮差资料相关系数很高，高低潮位相关系数高于0.98，潮差相关系数为0.972。本工程邻近高公岛海域，利用相关方程由连云港站1992-2011年最大潮差推算得到高公岛潮差极值序列，分析得知300年、100年和50年重现期潮差分别为6.22，6.06和5.97 m。本次数值模拟，按表1列出的计算工况组合，共计算了3种不同重现期下的流速过程，三者的流速分布特征基本相同，且50年一遇的流速基本小于100年一遇和300年一遇的流速。由于跨海大桥工程采用的是重现期100年和300年下的设计值，为减小篇幅，下文仅对这两种重现期的流速过程、流速特征展开分析，对重现期50年一遇的流速过程和特征不作详细讨论。

3.4 设计流速分析

重现期100年一遇时不同工况组合下的涨潮、落潮流场如图6所示。在100年一遇潮位无风浪工况下，大桥北侧接岸处在涨潮时受地形影响产生漩流，局部流速增大；大桥南侧接岸处以沿岸流为主，涨潮为SE向，落潮为NW向。

图6 工程区域及附近海域的涨潮落潮流场Fig.6 Flow fields of the project area and nearby area

对比图6(a），(b）与图6(c），(d）可以看出，在E向风浪作用下，工程区域及附近海域的涨潮落潮流场形态都有较大改变；由于E向风与海湾以南岸线夹角成锐角，在海湾以南的沿岸，涨落潮流均变为NW向的沿岸流。如图6(e），(f）所示，ENE向风浪作用下的流场形态与E向风浪作用时大致相同，但流速矢量略有减小。与E向、ENE向风浪不同，NE向风浪几乎垂直于海湾以南岸线，在涨潮时没有明显的沿岸流。由此可知，3种不同风浪对流场的影响不同。

为比较分析风和浪分别对工程区域流场的影响程度，列出100年一遇潮位下，有风无浪和无风有浪作用下的流场(图7）。图7与图6(a），(b）对比可知，在100年一遇潮位和风作用下，其同时刻的涨潮落潮流场变化较大：在海湾以南沿岸，涨潮流变为NW向的沿岸流，且流速值有增大；由于风的影响，落潮流有明显增强。在100年一遇潮位和波浪作用下，其同时刻的涨潮落潮流场变化较小：由于波浪影响，在海湾以南的沿岸SE向涨潮流消失，海湾以南的沿岸NW向落潮流稍有增强。

图7 100年一遇潮位下工程区域及附近海域涨潮落潮流场Fig.7 Flow fields of the project area and nearby the area under 100 years return period

1#～15#计算点的底面高程分布如图8所示，高程基面为当地理论最低潮面。在无风浪计算工况下，1#～15#计算点的最大流速与平均流速分布如图9(a），(b）所示。从不同重现期来看，300年一遇的最大流速值基本大于100年一遇的最大流速值。从计算点的不同位置来看，平均流速值呈现中间大、南北两边小的流速特征，这与水深值的分布特征相同，6#计算点水深值最大，其平均流速值也最大；最大流速值分布并不是呈现如上特征，这与最大流速值发生的时刻不同和各个计算点是否露滩有关。1#～3#计算点存在露滩现象，最大流速值发生在涨急时刻，4#～8#计算点无露滩，最大流速值发生在落急时刻；9#～14#计算点存在露滩现象，最大流速值发生在露滩前1 h。

在有风浪工况下，E向、ENE向、NE向风浪作用时，1#～15#计算点的100年一遇最大流速与平均流速分布如图9(c），(d）所示。由于风浪作用，引起近岸增水效应，计算点的流速值都有不同程度的增大。在不同方向风浪作用下，1#～15#计算点的流速值呈现如下特征：E向风浪作用时流速值最大，ENE向次之，NE向最小。1#～15#计算点中，5#计算点的最大流速值最大，其100年一遇最大流速值为0.76 m/s，300年一遇最大流速值为0.81 m/s。

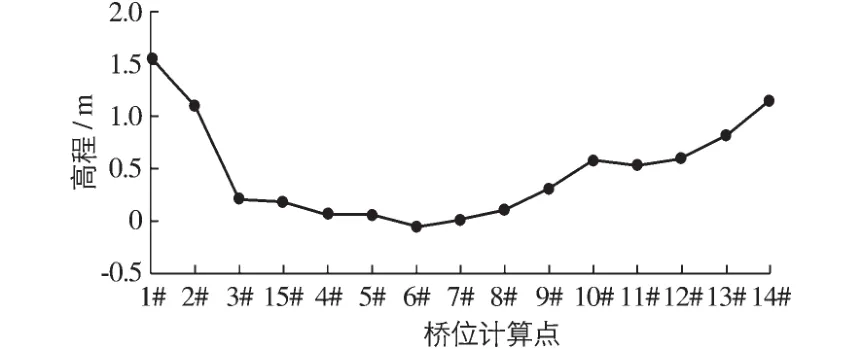
图8 1#～15#桥位计算点的高程分布Fig.8 Elevation of the calculation points

图9 有无风浪作用时1#～15#计算点的最大流速值与平均流速值分布Fig.9 The maximum and average current velocities of the calculation points with and without wind and waves

综合以上分析可知，在相应重现期下的风浪作用下，工程区域近岸会产生0.20～0.80 m的增水，流速值也相应增大。因此，通过本文的数值模拟研究，计算得到现状岸线边界条件下，重现期100年和300年时大桥工程位置最大流速值分别为0.76和0.81 m/s。

4 结 语

(1）利用有限体积法和干湿边界技术建立了一个二维潮流数学模型，用于潮间带地区跨海大桥设计流速的计算。通过模型验证和考虑不利风浪等多种工况下的数值模拟，计算得知，当工程区附近有排水设施时，工程位置最大流速值为1.25 m/s。

(2）工程海域内重现期300年一遇的流速普遍大于重现期100年一遇的流速，重现期100年一遇的流速大于重现期50年一遇的流速。但由于工程区域位于潮间带地区，不同重现期下的最大流速值差值和平均流速值差值较小。

(3）在有风浪作用情况下，大桥工程位置及其附近海域将会产生0.20～0.80 m的增水，并在风生流和波生流的影响下，流场会发生较大改变，各计算点的流速值也都相应增大。因此，对于潮间带地区设计流速的计算，必须考虑风浪的影响。

［1］苏慧，龚维明，梁书亭.苏通大桥短期观测流速在设计基准期内的应用［J］.中国工程科学，2006，8(7）：42-46.(SU Hui，GONG Wei-ming，LIANG Shu-ting.Short-range current velocity records to apply in the reference period for Sutong Bridge［J］.Engineering Science，2006，8(7）：42-46.(in Chinese））

［2］许德龙.额木尔河大桥水文计算浅析［J］.林业科技情报，2012，44(3）：132-138.(XU De-long.Hydrologic computation of Emuer River Bridge［J］.Forestry Science and Technology Information，2012，44(3）：132-138.(in Chinese））

［3］鲁海燕，潘存鸿，卢祥兴.钱塘江嘉绍大桥设计涨潮流速计算［J］.浙江水利科技，2008(4）：1-4.(LU Hai-yan，PAN Cun-hong，LU Xiang-xing.Computation of design velocity of Jiashao Bridge in the Qiantang River［J］.Zhejiang Hydrotechnics，2008(4）：1-4.(in Chinese））

［4］许雪峰，羊天柱，孙志林，等.杭州湾南岸浅滩的漫滩潮流数值模拟［J］.海洋科学，2012，36(4）：107-112.(XU Xuefeng，YANG Tian-zhu，SUN Zhi-lin.Simulation of floodplain flow on the south tideland of the Hangzhouwan Bay［J］.Marine Sciences，2012，36(4）：107-112.(in Chinese））

［5］白志刚，裴丽，阳磊.潮间带风电场水动力数值模拟［J］.港工技术，2012，49(3）：1-4.(BAI Zhi-gang，PEI Li，YANG Lei.Hydrodynamic numerical simulation for wind farm in intertidal zone［J］.Port Engineering Technology，2012，49(3）：1-4. (in Chinese））

［6］冯静.MIKE21FM数值模型在海洋工程环境影响评价中的应用研究［D］.青岛：中国海洋大学，2011.(FENG Jing. Application of MIKE21FM numerical model in environmental impact assessment of ocean engineering［D］.Qingdao：Ocean University of China，2011.(in Chinese））

［7］郭凤清，屈寒飞，曾辉，等.基于MIKE21的潖江蓄滞洪区洪水危险性快速预测［J］.自然灾害学报，2013(3）：144-152. (GUO Feng-qing，QU Han-fei，ZENG Hui，et al.Flood hazard forecast of Pajiang River flood storage and detention basin based on MIKE21［J］.Journal of Natural Disasters，2013(3）：144-152.(in Chinese））

［8］黄世昌，胡金春.岱山跨海大桥水文分析计算专题［R］.杭州：浙江省水利河口研究院，2008.(HUANG Shi-chang，HU Jin-chun.Hydrological analysis report for Daishan bridge［R］.Hangzhou：Zhejiang Institute of Hydraulic&Estuary，2008.(in Chinese））

［9］侯虹波，陈永平，张长宽.江苏沿海近岸台风浪数值模拟［J］.水运工程，2013(4）：13-19.(HOU Hong-bo，CHEN Yongping，ZHANG Chang-kuan.Numerical simulation of typhoon waves along Jiangsu coast［J］.Port&Waterway Engineering，2013 (4）：13-19.(in Chinese））

［10］徐宇达，陈则明，张锦灿.连云港核电厂工程水域水文观测报告［R］.南京：江苏省水文水资源勘测局，南京水利科学研究院，1998.(XU Yu-da，CHEN Ze-ming，ZHANG Jin-can.Hydrological observation report for the water area of Lianyungang nuclear power plant project［R］.Nanjing：Jiangsu Province Hydrology and Water Resources Investigation Bureau，Nanjing Hydraulic Research Institute，1998.(in Chinese））

Calculation and analysis of design current velocity for Lianyungang Haibin bridge in intertidal zone

ZHAI Jian-feng1，2，DONG Pei-hua1，2，XIONG Wei1，2，DONG Jia1，2
(1.Jiangsu Proυincial Communications Planning and Design Institute Co.，Ltd.，Nanjing 210005，China；2.Water Transport Engineering Research Center of Jiangsu Proυince，Nanjing 211100，China）

As one of the important parameters in the design of the bridge，the design current velocity is closely related to the safety of the bridge construction and its safe operation.Usually two kinds of prediction methods including analysis by the measured data and calculation by a mathematical model are used in the engineering practices.In order to ensure the safety of the bridge construction and normal operation，it is necessary to accurately predict the design current velocity.It is an available approach to use the mathematical model to predict possible maximum current velocity in the construction area.Therefore the mathematical model calculating the tidal current in the engineering sea area is developed by use of 2D shallow water equation and wet/dry boundary treatment technique based on the finite volume method，and the model verification is carried out using the measured data.On this basis，taking account of combinations of different working conditions with and without wind and waves，the design current velocity for the bridge construction position in the intertidal zone at different recurrence intervals is calculated and analyzed，which has provided important parameters for the bridge design and physical model tests. The calculated and analyzed results show that the key factors such as wind and waves should be considered in calculating design current velocity for bridge construction because they would cause greater impacts on the flow field in the intertidal zone.

sea-crossing bridge；intertidal zone；wet/dry boundary；recurrence intervals；numerical simulation；action by wind and waves

TV131.3；P731.21 文献标心码：A

1009-640X(2014）03-0062-08

2013-10-14

江苏省交通科技重大专项资助项目：江苏沿海建港条件及关键技术集成研究(2011Y01）

翟剑峰(1975-），男，安徽芜湖人，高级工程师，主要从事水运工程技术的规划、咨询和相关技术研发等工作。通信作者：熊伟(xw_7816@126.com）