利用PLAXIS软件计算考虑降雨的边坡稳定性

孔郁斐，周梦佳，宋二祥，杨 军，张龙英，施洪刚，刘 剑

(1.清华大学 土木工程安全与耐久教育部重点实验室，北京 100084；2.中国建筑股份有限公司，北京100000）

利用PLAXIS软件计算考虑降雨的边坡稳定性

孔郁斐1，周梦佳1，宋二祥1，杨 军1，张龙英2，施洪刚2，刘 剑2

(1.清华大学 土木工程安全与耐久教育部重点实验室，北京 100084；2.中国建筑股份有限公司，北京100000）

降雨条件下的边坡稳定性分析，需要同时考虑水的渗流与边坡内力进行耦合计算。非饱和土的特殊性质增加了计算难度，其渗透性、强度都会随含水量的变化而变化。介绍了非饱和土的有效应力原理，并比较了PLAXIS和Geo-Studio两款软件使用的有效应力原理和破坏准则的异同。PLAXIS软件中用有限元法计算非饱和土的渗流问题，利用简化的Bishop有效应力公式进行固结、变形及边坡稳定性计算，土体本构关系根据需要选用；Geo-Studio软件中也使用有限元法计算非饱和渗流，但其边坡安全系数计算方法为极限平衡法，强度准则为Fredlund双变量理论。最后结合算例详细介绍了PLAXIS软件中进行非饱和土边坡计算的建模方法。算例显示，PLAXIS软件中建立的计算模型可以准确反映降雨过程中边坡安全系数的变化规律。今后的工程设计中，可以考虑使用这一软件进行非饱和土边坡设计计算。

非饱和土；降雨渗流；土坡稳定；耦合计算；PLAXIS软件；Geo-Studio软件

降雨型滑坡是常见的自然灾害，非饱和土边坡在降雨过程中安全系数逐渐降低。降雨条件下的边坡稳定性计算是渗流分析和受力分析的耦合问题。土的渗透系数、强度都会随其含水量变化而变化，因此瞬态渗流计算和安全系数计算中都必须考虑非饱和土的特殊性质。经过20世纪的发展，非饱和土理论已比较完善［1］，并向实用化迈进。岩土工程相关的数值计算软件也正逐渐开发与非饱和土有关的功能，比较知名的PLAXIS、Geo-Studio等软件，都能进行非饱和土边坡稳定性计算。

Geo-Studio是加拿大开发的用于岩土工程和岩土环境模拟计算的软件，较早涉足非饱和土计算。它包括8个模块，其中SEEP/W模块可进行饱和/非饱和的二维稳态/瞬态渗流计算，得出孔隙水压分布［2］；然后将孔压计算结果导入SLOPE/W模块，利用极限平衡法计算边坡安全系数［3］。对均质土坡而言，降雨时表层土壤首先浸润，深层土壤受影响较晚，故水分分布不均匀，使用“圆弧滑移面”的假设不一定合适；另外很多坡体本身就不均匀，真实滑移面形状很复杂［4］，基于“圆弧滑移面”假设的极限平衡法不适用，SLOPE/W虽然也能搜索任意形状滑移面，但有时算法不稳定，结果可靠性有待验证。

荷兰开发的岩土工程有限元设计计算软件PLAXIS使用“强度折减有限元法”计算边坡稳定性［5］，计算出的滑移面更接近真实滑移面，因此对非均匀的土坡使用这一方法结果更可靠。PLAXIS可以进行2D/3D的弹塑性计算、渗流计算、固结分析、安全分析、动力计算等，近几年增加了非饱和土的计算功能，其2011版可以将非饱和土渗流计算和安全系数的强度折减有限元计算耦合［6］，值得探索和尝试。

本文将首先介绍非饱和土有效应力原理，这是数值计算的重要理论基础，并对PLAXIS与Geo-Studio进行了比较，接着详细介绍PLAXIS中的建模方法，并结合算例讨论PLAXIS的计算结果。

1 非饱和土有效应力原理

如前所述，边坡的渗流计算、安全系数计算都要考虑非饱和土的特殊性质，问题复杂，影响因素众多，吴宏伟等［7-8］曾就相关的难点、计算方法作过详细的阐释，本文不多介绍。两个相关商业软件的主要区别在于使用的有效应力原理和强度准则不同，本节将重点介绍其区别。

饱和土的有效应力原理由太沙基提出［9-10］，该理论认为：①饱和土体内任意一平面上受到的总应力可分为有效应力和孔隙水压力两部分，在同一点处水压向各方向都是相等的；②土的变形(压缩）与强度的变化都只取决于有效应力变化，其表达式为：

有学者将其扩展到孔隙中有多种流体(水、油、气等）的情况［11］：

该式又叫“广义有效应力公式”。式中：uβ为第β种流体的分压，αβ为其分项系数，表征其在总应力中的贡献。不难理解，有多种流体共同存在时，每种流体分压的分项系数αβ≤1。土是由土骨架、水、空气组成的三相体：饱和土中仅有水，饱和度S=1，αw=1，αs=0，式(2）退化为式(1）；干燥土仅有空气，S=0，αa=1，αw= 0；非饱和土的2个系数均在0～1之间变化。

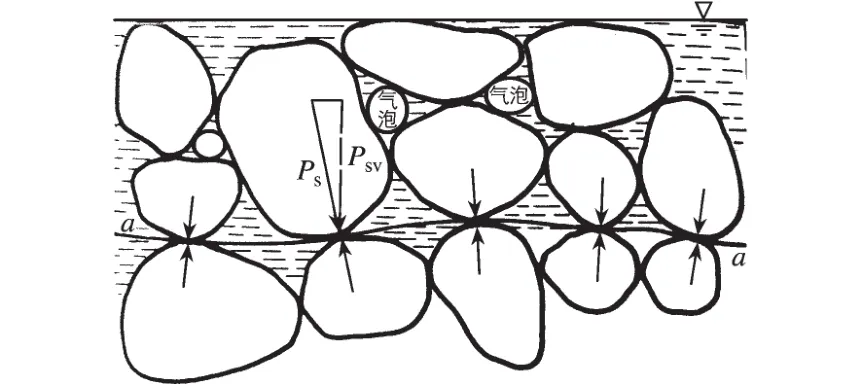
图1 饱和度较大的非饱和土Fig.1 Sketch of the nearly-saturated soil

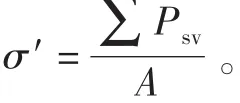
考察a-a面以上的土骨架，由土骨架受力平衡可得：

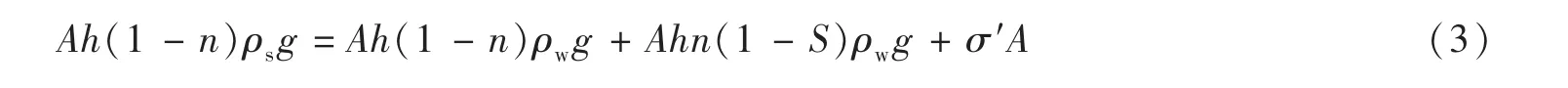
故

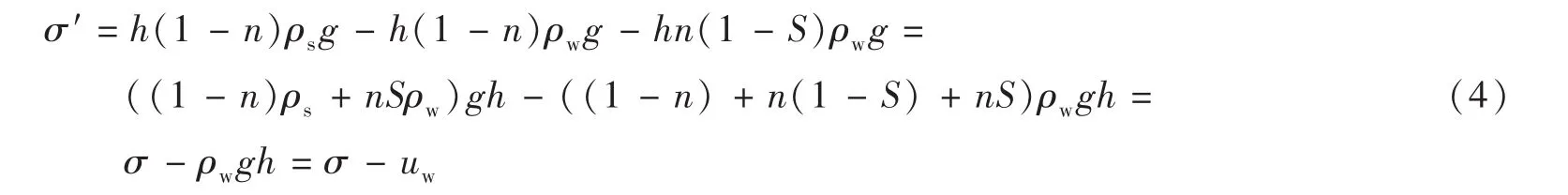
此时仍然有αw=1，αa=0，与饱和土类似。

但若土中空气较多，内部空气不再只以气泡的形式存在、能与大气连通，则土中气体的平衡方程中不仅包含浮力、土骨架作用力，还包含外部空气压力以及表面张力，有效应力就更加复杂了。1960年毕肖普等提出了修正的有效应力公式(Bishop有效应力公式）：

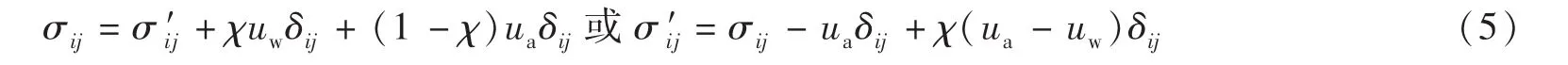
式中：χ是与饱和度有关的系数，饱和土χ=1，干土χ=0。这一公式是式(2）的简化形式，在式(2）中令αw=χ，αa=1-χ可得到式(5）。式中σij-uaδij被称作净法向应力张量，ua-uw被称作基质吸力。土饱和时，ua=uw，净法向应力等于饱和土的有效应力，基质吸力为零；土不饱和时，基质吸力为正。

将Bishop有效应力公式代入摩尔-库伦准则(τ=c′+σ′tanφ′）可得基于Bishop有效应力的摩尔-库伦准则：

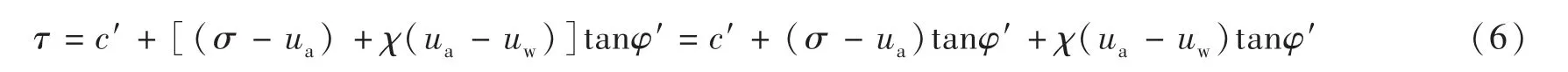
式中：φ′为有效内摩擦角，χtanφ′体现了基质吸力对抗剪强度的贡献。

从数学上看这一简化非常简单，但在工程上它非常有意义，我们可以在不同饱和度下进行土的三轴试验，确定函数χ(S），就可以得到非饱和土的有效应力，再根据“土的变形及强度变化都只取决于有效应力的变化”的假设就可以将原有的饱和土应力应变分析的理论应用于非饱和土。Zerhouni总结了几种不同土的χ-S关系曲线(见图2），这些数据均由试验测得［12］，可见χ(S）函数没有特别的规律可言。1和4两种土的饱和度达到90%左右时，χ=1，与图1的情形有相似之处。

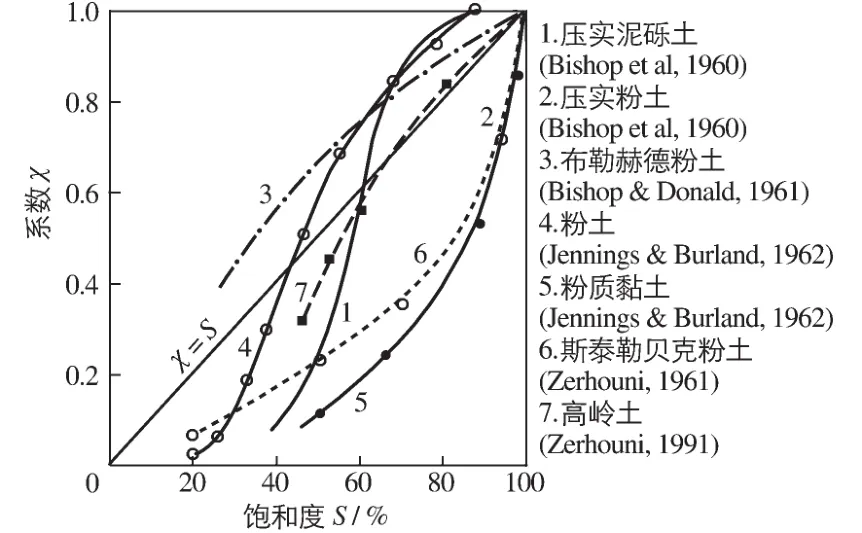
图2 几种不同土的χ-S关系曲线Fig.2 Curves for several different soils

不过随着研究的深入，人们也发现Bishop有效应力公式存在一定的局限性。例如，它无法解释一些土在浸湿过程中的体缩现象：保持土的总应力不变，使土浸湿，则土中有效应力减小，应变本应持续增加，但某些土会先湿胀、再湿陷。所以有人提出疑问：在非饱和土中直接照搬饱和土的有效应力的概念似乎有些牵强，当水和空气共同存在时，针对饱和土所作的“土的变形及强度变化都只取决于有效应力的变化”假设还成立么?

不一定成立。在饱和土中水的体积应变很小，体变的内力功可以忽略，土进入塑性以后土骨架之间的摩擦使能量耗散；非饱和土中空气可以压缩，空气-水的界面可以变形，空气的压缩和表面张力做功都会消耗能量，故耗能能力受到流体性质的影响，有效应力不再是唯一的决定因素。

D.G.Fredlund等［1］提出，可以用净法向应力和基质吸力两个独立的应力张量来描述土的状态，克服单一有效应力变量的缺陷，在Fredlund双变量理论中，土的应力应变关系如下［1］：

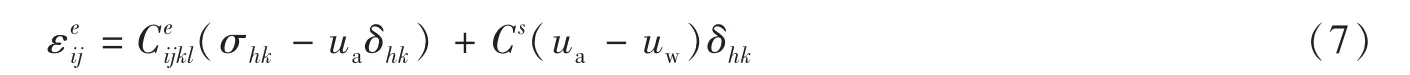
似乎有了这个公式之后，对非饱和土的计算就能得心应手了，其实不然，要获得完整的参数着实不易，两个应力张量让破坏面更难描述。比较常用的还是更简单直观的假设：线弹性、理想弹塑性或者刚塑性。

摩尔-库伦准则也被扩展到双变量理论中(扩展的摩尔-库伦准则）：

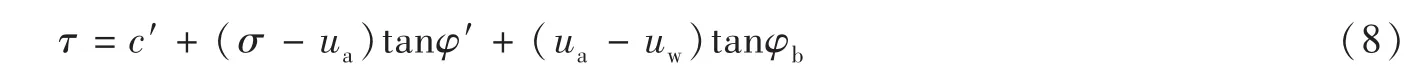
式中：tanφb表征基质吸力对抗剪强度的贡献，且φb并非常数，随饱和度变化。

沈珠江院士曾指出，既然φb并非常数，在强度准则里式(8）就不见得比式(6）优越［13］。很多学者提出了更为复杂的强度公式，但现在仍然是扩展的摩尔-库伦准则使用最广泛。

PLAXIS和Geo-Studio分别使用了以上两种有效应力理论，并且都作了简化。

PLAXIS中使用了Bishop有效应力公式，由于χ(S）函数很复杂，直接令χ=S；也就是说在图2中取对角线，这与实际情况存在一些差距，最接近图2中的第7种土(White Clay），用于其他土时需要对参数进行评估。这一有效应力可以用于多种本构模型，当然最简单的是理想弹塑性模型及摩尔-库伦准则。虽然Bishop有效应力公式有局限性，但是处理非特殊土时，这一理论是能够胜任的。

Geo-Studio中使用了Fredlund双变量理论，并假设φb为常数，计算时需根据滑移面穿过区域的含水量变化范围，选取合适的φb，否则极易低估或高估基质吸力对强度的贡献。虽然Fredlund双变量理论比Bishop公式有优势，但使用极限平衡法计算边坡稳定性时不涉及土的应力-应变关系，优势便无从体现了。

在此也介绍一下非饱和土的土水特征曲线(SWCC）和渗透性函数。非饱和土的体积含水率θw，基质吸力ψ(=ua-uw），渗透系数k都会随着饱和度S变化。ψ(θw）或ψ(S）函数关系即为“土水特征曲线”，k(S）或k(ψ）函数关系即为“渗透性函数”。这两种函数也较为复杂，研究者们曾提出很多种函数形式，比较知名的有Gardner方程、van Genuchten方程［14］、Fredlund-Xing方程等［15］。

无论如何，用两款软件进行计算时都应谨慎选用数据。除了有效应力原理、强度准则和安全系数计算方法，在其他方面这两款软件有很多相似之处，都能进行多种边界条件设定、内置了较多土水特征曲线和渗透性函数的方程。值得一提的是，PLAXIS还内置了数个和非饱和土数据库，如USDA(美国农业部）数据库、Hypres数据库等，方便用户在试验数据有限的情况下选取合适的参数快速建模。

2 PLAXIS建模与计算

在PLAXIS 2D(2011）中建立如图3所示的均质边坡模型，模型大小为30 m×10 m，边坡高5 m，长8 m，地下水位位于坡脚下方3 m处，网格划分疏密程度为“很细”；模型为平面应变模型，单元为15节点单元。土体类型选用USDA数据库中的“沃土”：粒径小于2 μm的质量占总质量的比例p0.0002=20%，2～50 μm的占40%，50 μm～2 mm的占40%，按国内分类属于细粒土。

土的饱和渗透系数ksat=0.247 9 m/d，土的渗透性函数和土水特征曲线使用van Genuchten方程拟合［16］，结果如图4所示，图中两条曲线由软件自动生成，其中kr=k/ksat表示相对渗透系数，为无量纲量，S为饱和度。容易看出饱和度为0.7时基质吸力水头约为0.5 m，相对渗透系数为0.01。

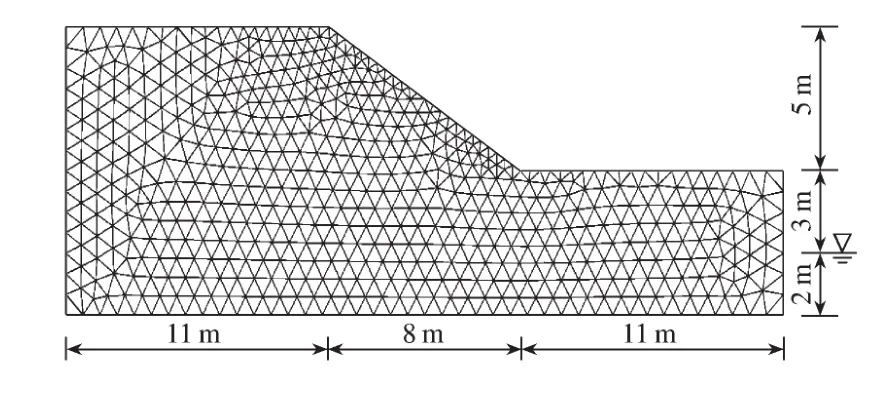
图3 PLAXIS中的边坡模型及网格Fig.3 The slope model and mesh used in PLAXIS

图4 模型中土的渗透性函数(左）和土水特征曲线(右）Fig.4 Permeability function and SWCC used in the model

对于一个地下水位恒定、表面没有降雨/蒸发的边坡而言，其地下水位以上的基质吸力分布是线性的，水位以上x处基质吸力水头为x。但天然边坡的基质吸力水头一般有上限，上限为零点几米到几米不等，可以在表面定义一个极小的入渗速率(或称“虚拟降水”），使得内部稳态渗流时基质吸力最大值在我们需要的范围内。本算例计算中我们首先进行稳态渗流计算，令上表面有1 mm/d的虚拟降水，这样边坡中最大基质吸力水头为0.719。

计算以下两工况：工况1，降雨速率为50 mm/d，持续时间分别为0.5，1.0和2.0 d；工况2，降雨速率为10 mm/d，持续时间分别为2.5，5.0和10.0 d。两种工况最后的总降雨量均为100 mm。

表1和图5展示了算例中的边坡在不同工况下的安全系数、滑移面深度计算结果。图6、图7分别为不同时刻边坡的基质吸力分布和滑移面，计算所得的7组滑移面都比较浅，工况1中滑移面深度从1.82 m降至1.11 m，降雨结束时安全系数接近1.00，这个理想的边坡已经非常危险了；工况2中滑移面深度从1.82降至1.45 m。

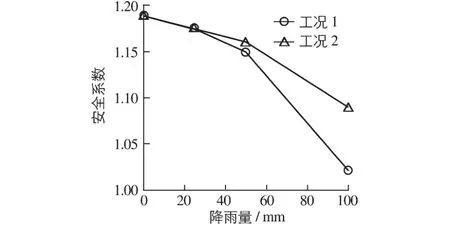
图5 两种工况下边坡安全系数随降雨量的变化Fig.5 Variation of safety factor with rainfall in different working conditions

表1 安全系数、滑移面深度随降雨量的变化Tab.1 Variations of safety factor and depth of sliding surface with rainfall

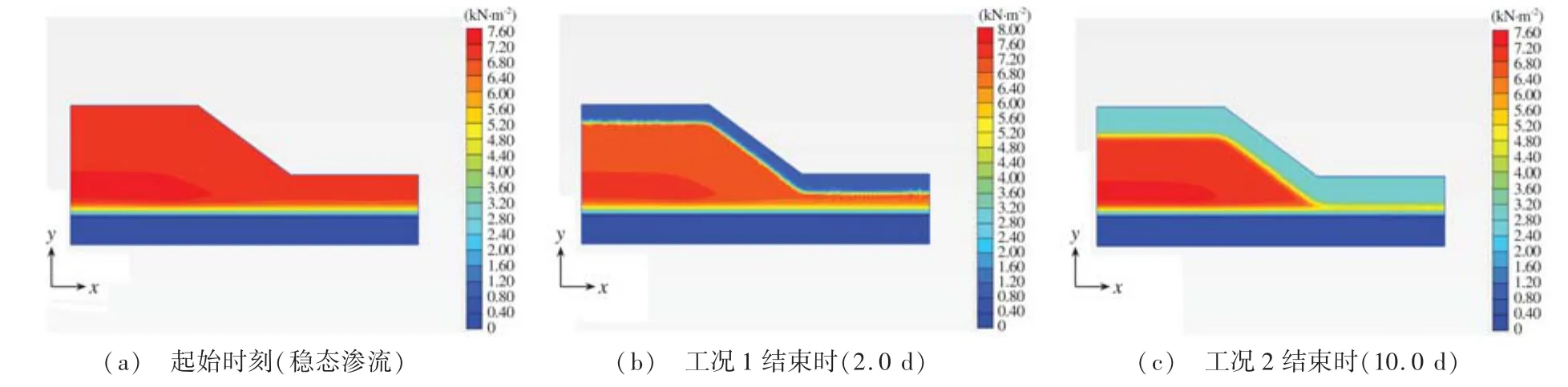
图6 不同工况下的边坡基质吸力分布Fig.6 Matric suction distribution in different working conditions

图7 不同时刻强度折减法计算得到的边坡位移云图Fig.7 Shadings of displacements from φ/c reduction calculation

可以看出降雨过程中该边坡安全系数明显减小，且工况1中安全系数降幅更大。随着雨水入渗，坡中土的含水量会自上而下逐渐增加，随着饱和度的提高，土的基质吸力下降、有效应力减小，强度降低，因此边坡的安全系数会降低。降低的速率取决于很多因素，在总降雨量相同的情况下，如果降雨速率快、时间短(工况1），雨水会主要集中在土体上部，浅层滑移面经过处的土的强度降幅大，更容易发生浅层滑坡；如果降雨速率慢，雨水有充足的时间下渗至更深处，浅层滑移面经过处的土的强度降幅小。这与笔者此前用Geo-Studio计算发现的规律相符［17］。

3 结 语

本文总结了非饱和土有效应力原理的不同形式，在此基础上比较了PLAXIS和Geo-Studio两款软件计算原理的差异，并介绍了在PLAXIS中进行考虑降雨的边坡稳定性计算的建模方法。通过本文的分析可以发现，PLAXIS中使用简化的Bishop有效应力原理可以反映非饱和土的性质，在使用中需要注意合理选取参数，与Geo-Studio使用的双变量理论相比，两款软件的强度准则没有明显的优劣之分。算例显示，PLAXIS中建立的计算模型可以正确反映降雨过程中边坡安全系数的变化规律。在今后的工程设计中，可以考虑使用PLAXIS软件进行非饱和土边坡设计计算。

参 考 文 献：

［1］FREDLUND D G，RAHARDJO H.Soil mechanics for unsaturated soils［M］.New York：John Wiley&Sons，1993.

［2］GEO-SLOPE International Ltd.Seepage modeling with SEEP/W 2007-an engineering methodology［M］.3rd ed.Canada：GEOSLOPE International Ltd，2008.

［3］GEO-SLOPE International Ltd.Stability modeling with SLOPE/W 2007 version-an engineering methodology［M］.3rd ed. Canada：GEO-SLOPE International Ltd，2008.

［4］张建民，王睿，张嘎.降雨条件下含软弱夹层土坡的离心模型试验研究［J］.岩土工程学报，2010(10）：1582-1587. (ZHANG Jian-min，WANG Rui，ZHANG Ga.Centrifuge modeling of rainfall-induced deformation of slopes with weak layers［J］.Chinese Journal of Geotechnical Engineering，2010(10）：1582-1587.(in Chinese））

［5］宋二祥.土工结构安全系数的有限元计算［J］.岩土工程学报，1997，19(2）：1-7.(SONG Er-xiang.Finite element

analysis of safety factor for soil structures［J］.Chinese Journal of Geotechnical Engineering，1997，19(2）：1-7.(in Chinese））

［6］PLAXIS.PLAXIS Scientific Manual 2011［M］.［S.l.］：［s.n.］，2011.

［7］吴宏伟，陈守义，庞宇威.雨水入渗对非饱和土坡稳定性影响的参数研究［J］.岩土力学，1999，20(1）：1-14.(WU Hong-wei，CHEN Shou-yi，PANG Yu-wei.Parametric study of effects of rain infiltration on unsaturated slopes［J］.Rock and Soil Mechanics，1999，20(1）：1-14.(in Chinese））

［8］NG C W W，SHI Q.Influence of rainfall intensity and duration on slope stability in unsaturated soils［J］.Quarterly Journal of Engineering Geology，1998，31(2）：105-113.

［9］TERZAGHI K.Theoretical soil mechanics［M］.New York：John Wiley&Sons，1943.

［10］陈仲颐，周景星，王洪瑾.土力学［M］.北京：清华大学出版社，1994.(CHEN Zhong-yi，ZHOU Jing-xing，WANG Hongjin.Soil mechanics［M］.Beijing：Tsinghua University Press，1994.(in Chinese））

［11］NUTH M，LALOUI L.Effective stress concept in unsaturated soils：Clarification and validation of a unified framework［J］. International Journal for Numerical and Analytical Methods in Geomechanics，2008，32(7）：771-801.

［12］ZERHOUNI M I.Rôle de la pression interstitielle négative dans le comportement des sols-Application au calcul des routes［D］.Paris：Ecole Centrale Paris，1991.

［13］沈珠江.当前非饱和土力学研究中的若干问题［C］∥区域性土的岩土工程问题学术论文集.北京：原子能出版社，1996：1-9.(SHEN Zhu-jiang.Current issues of unsaturated soil mechanics［C］∥Regional Colloquium on Soil Geotechnical Proceedings.Beijing：Atomic Energy Press，1996：1-9.(in Chinese））

［14］VAN GENUCHTEN M T.A closed-form equation for predicting the hydraulic conductivity of unsaturated soils［J］.Soil Science Society of America Journal，1980，44(5）：892-898.

［15］ LEONG E C，RAHARDJO H.Review of soil-water characteristic curve equations［J］.Journal of Geotechnical and Geoenvironmental Engineering，1997，123(12）：1106-1117.

［16］GALAVI V.Groundwater flow，fully coupled flow deformation and undrained analyses in PLAXIS 2D and 3D［R］.Delft：Research Department，PLAXIS，2010.

［17］孔郁斐.降雨对非饱和土边坡稳定性影响研究［D］.北京：清华大学，2012.(KONG Yu-fei.Rainfall′s effect on the

stability of unsaturated slopes［D］.Beijing：Tsinghua University，2012.(in Chinese））

Slope stability analysis in consideration of rainfall influence based on PLAXIS software

KONG Yu-fei1，ZHOU Meng-jia1，SONG Er-xiang1，YANG Jun1，ZHANG Long-ying2，SHI Hong-gang2，LIU Jian2
(1.Key Laboratory of Ciυil Engineering Safety and Durability of China Ministry of Education，Tsinghua Uniυersity，Beijing 100084，China；2.China State Construction Engineering Co.，Ltd.，Beijing 100000，China）

In order to analyze the slope stability in consideration of the rainfall influences，it is necessary to couple the calculation of the rainfall infiltration and the slope internal force.Special characteristics of the unsaturated soils make the calculation more complex，because the soil′s hydraulic permeability and strength would change with moisture content.In the paper the principle of the effective stress of the unsaturated soils is introduced.The similarities and differences of the principle of effective stress and failure criteria used in the PLAXIS and Geo-Studio softwares are compared.In PLAXIS，the finite element method is used for unsaturated seepage calculation and a simplified Bishop effective stress formula is applied to the calculation of consolidation，deformation and slope stability.The constitutive models for the saturated soils can be used on that basis.The Geo-Studio uses the finite element method for the unsaturated seepage calculation and the limit equilibrium method for the calculation of the slope safety factor，in consideration of Fredlund′s bilinear strength criterion.Finally，details of the method for modeling the unsaturated slopes in PLAXIS are presented with calculation examples.The calculation examples show that the models in PLAXIS can accurately reflect rainfall-induced slope safety factor variation.Therefore，this software can be adopted for the unsaturated soil slope design and calculation in the future.

unsaturated soil；rainfall infiltration；slope stability；coupling calculation；PLAXIS software；Geo-Studio software

TU413.6+2 文献标心码：A

1009-640X(2014）03-0070-07

2013-11-12

孔郁斐(1991-），男，江苏泰兴人，博士研究生，主要从事岩土工程方面的研究。E-mail：kyf12@mails.tinghua.edu.cn