圆形截面钢管钢筋混凝土构件承载力的计算

王廷伟，贡金鑫，吴志良，朱晓瑜

(1.大连理工大学 建设工程学部，辽宁 大连 116024；2.中交第三航务勘察设计院有限公司，上海200032）

圆形截面钢管钢筋混凝土构件承载力的计算

王廷伟1，贡金鑫1，吴志良2，朱晓瑜1

(1.大连理工大学 建设工程学部，辽宁 大连 116024；2.中交第三航务勘察设计院有限公司，上海200032）

对8个圆形截面钢管钢筋混凝土构件进行了轴心受压和偏心受压试验，采用有限元法和纤维模型法对构件承载力进行了计算，提出了圆形截面钢管钢筋混凝土构件承载力的简化计算方法。研究表明，圆形截面钢管钢筋混凝土具有与钢管混凝土和钢筋混凝土相同的特点，按有限元法计算的构件承载力偏小，而按纤维模型法计算的构件承载力与试验结果符合较好。圆形截面钢管钢筋混凝土构件的承载力可通过将钢管视为普通钢筋，将混凝土视为钢管约束混凝土的双层钢筋约束混凝土构件，采用圆形截面钢筋混凝土构件承载力的计算方法进行简化计算。按简化方法计算的圆形截面钢管钢筋混凝土构件的承载力也与试验结果符合较好。

钢管钢筋混凝土；圆形截面；承载力；有限元法；纤维模型法

20世纪90年代，嵌岩桩作为一种特定的桩基类型在我国得到广泛应用，目前在港口工程及桥梁工程的应用也越来越多。工程中为减少桩的数量，多采用大直径的嵌岩桩，大直径嵌岩桩具有承载力高、桩径大、沉降小、抗震性能好等优点。在沉桩过程中，为防止钢套筒发生圈边、翘曲等情况，一般要采用厚度较大的钢套筒，但较厚的套筒壁增加了工程造价，像深圳的盐田港码头工程、华能福州电厂码头工程，嵌岩桩钢套筒的最大壁厚可达20 mm。在嵌岩桩承载力设计中，由于缺乏理论指导和计算公式，目前一般忽略钢套筒的承载力，只考虑钢筋混凝土桩的承载力。而实际上，钢套筒与桩内钢筋混凝土共同承担荷载，即使钢套管有一定部分受到腐蚀，但剩余部分仍具有很大的承载力。所以，如果设计中考虑套筒的作用，可减少桩内配筋数量，大大降低工程造价。由钢套筒与桩内钢筋混凝土构成的构件是钢管钢筋混凝土构件。钢管混凝土和钢筋混凝土已经有相关的标准和设计规范，但没有钢管钢筋混凝土构件承载力的计算方法，目前关于钢管钢筋混凝土承载力的研究也很少，已有的一些研究［1-7］主要针对的是钢管钢筋混凝土构件的轴心受压性能，缺乏对钢管钢筋混凝土构件的偏心受压性能的研究。本文对8个圆截面钢管钢筋混凝土试件进行了试验研究和理论分析，在此基础上提出钢管钢筋混凝土构件承载力的计算方法。

1 试验研究

1.1 试件设计

试验共设计了8根钢管钢筋混凝土试件，包括轴心受压和偏心受压试验，试件的钢管尺寸、钢筋直径及构件偏心距如表1所示。钢管采用Q345钢，含钢率为12.8%，屈服强度设计值为310 N/mm2；纵筋采用HRB335级钢筋，配筋率为3.93%，沿试件圆周均匀布置，屈服强度设计值为300 N/mm2；混凝土强度等级为C40防冻混凝土，抗压强度设计值为19.1 N/mm2。混凝土砂率为38.9%，水胶比为0.31，混凝土各种成分质量比为：水泥：粉煤灰：砂：石：水=1：0.221：1.829：2.727：0.374，单位立方米混凝土的质量为2 384.4 kg。试验前对钢管、钢筋和混凝土强度进行了试验，实测各材料强度值为：钢管fyt=345 MPa，钢筋fyt=322 MPa，混凝土fct=36.1 MPa。钢管钢筋混凝土试件的尺寸和配筋情况如图1所示。

表1 试件参数Tab.1 Parameters of the specimens

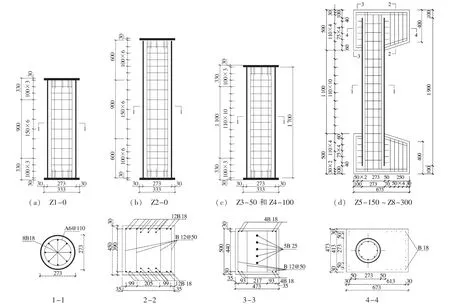
图1 试件尺寸和配筋(单位：mm）Fig.1 Dimension and reinforcement of the specimens(unit：mm）

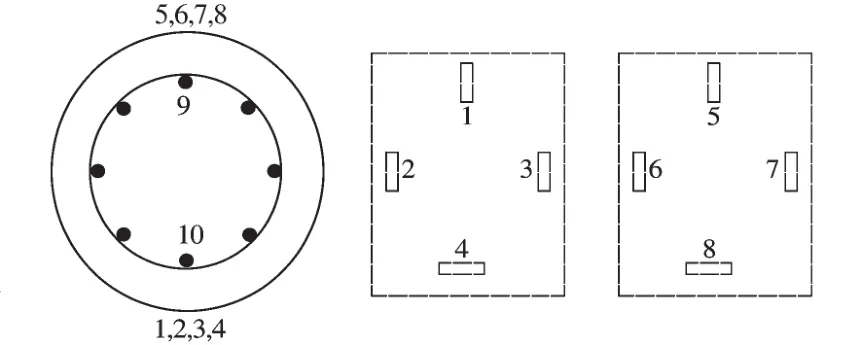
图2 试件应变片布置Fig.2 Placement of strain gages

为保证合理传力及偏心施加荷载，轴心受压试件Z1-0和Z2-0及偏心距较小的试件Z3-50和Z4-100两端各设置一个30 mm厚的钢板，偏心距较大的试件Z5-150～Z8-300两端做成钢筋混凝土墩。为保证钢管与混凝土共同受力，钢管两端外壁每隔90°设置一排长70 mm的Φ25螺纹钢筋，预埋钢筋和纵向受力筋末端设置180°弯钩以增加锚固强度。每个试件中高截面两侧受弯平面钢管的纵向和环向布置8个电阻应变片，每侧4个(图2中1-4号测点及5-8号测点），包含3个纵向应变片和1个环向应变片；试件中高截面纵筋贴2个应变片，如图2中9和10号测点所示。

1.2 试验装置及加载方式

试验在大连理工大学结构实验室进行。试验所用设备包括1 000 t万能试验机、IMC动态应变测试系统、测控软件SuperTestSystem2011、电阻应变片和位移传感器等。试验采集的数据包括钢管纵向、横向应变，钢筋应变、试件中高截面的挠度及施加的竖向荷载。

试验采用分级单调加载，开始时每级荷载为预估最大承载力的10%，接近60%的最大荷载时，每级荷载改为按预估最大荷载的5%施加，临近最大荷载时荷载步长进一步减小。当荷载达到最大值时，试验机压力表指针开始回转，仍然继续向油缸送油，并不断记录仪表读数和相应的荷载值，直至试件变形很大才停止试验。每次加载到预定荷载后，试验机保持荷载值，持荷2 min后再开始读取数值。所有试件均采用一次性加载至破坏。各试件的加载方式如图3所示。1.3 试验过程及试件破坏状态

图3 试件加载Fig.3 Loading of the specimens

试验过程中，随着荷载的增加，Z1-0和Z2-0轴心受压试件在荷载达到2 500 kN时，钢管中部开始有微凸，但是此凸出量始终不大，直到荷载达到极限荷载时，试件外观没有明显变化。Z3-50～Z8-300偏心受压试件，从刚加荷载开始就有挠度产生，随着偏心距增大，从Z3-50～Z8-300试件，挠度值依次增大，承载力依次降低。

1.4 应变变化规律

试验中钢管和钢筋的荷载-应变关系如图4(a）～(h）所示，其中1～9号为应变片的编号。

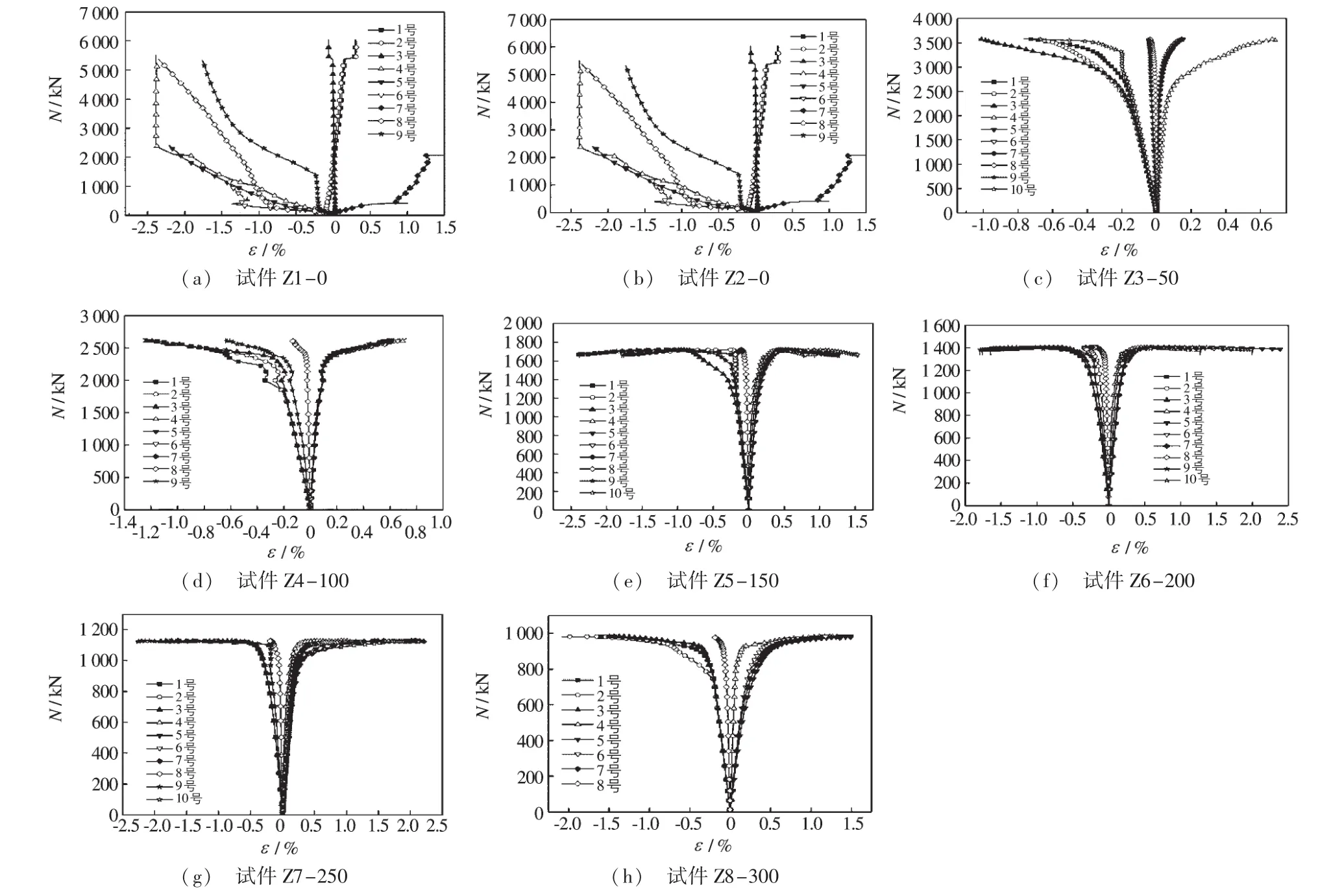
图4 荷载-应变曲线Fig.4 Load versus strain relationship of the specimens

由图可见，随荷载的增加应变分两个阶段变化。在达到极限荷载之前，各测点应变差别较小，荷载与应变基本呈线性关系；达到屈服荷载时，钢管的纵向和环向应力及钢筋的应力均接近或达到屈服强度，构件出现明显的塑性变形；进入塑性变形阶段，钢管环向应变迅速增加，增加速度快于纵向应变，说明钢管钢筋混凝土构件在受力初期，钢管对混凝土的约束并不是很明显，随着变形增大，当混凝土的横向变形系数超过钢材的横向变形系数时，钢管对混凝土的约束作用才开始明显，使混凝土处于三轴受压状态，延缓了核心混凝土的破坏，使钢管钢筋混凝土试件体现出良好的塑性变形能力。

1.5 试件承载力

表2给出了钢管钢筋混凝土试件的试验结果，其中的荷载N为试件承受的最大轴力，中高截面挠度f为荷载最大时的挠度。

表2 试件试验结果Tab.2 Test results of the specimens

2 理论分析

2.1 理论分析方法

本文采用了3种方法对钢管钢筋混凝土构件的承载力进行计算，具体方法和分析采用的材料本构模型、强度模型和参数如下。

2.1.1有限元法 有限元方法采用Abaqus软件，钢材和钢筋采用Abaqus软件中提供的等向弹塑性模型，混凝土采用Abaqus软件提供的塑性损伤模型。

2.1.2纤维模型法 纤维模型法能够比较准确地模拟钢筋混凝土构件和钢管混凝土构件从加载到破坏的过程，其关键是合理确定组成构件各材料的本构关系。

钢材采用下式表示的应力-应变关系［8］，如图5(a）所示：

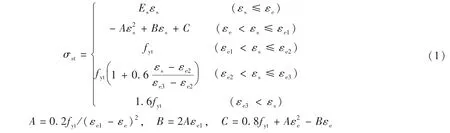
式中：σs为钢材应力；Es为钢材的弹性模量，取2.06×105MPa；εs为钢材应变；εe=0.8fyt/Es；εe1为与钢材屈服极限对应的应变，εe1=1.5εe；εe2为钢材应力应变曲线塑性段结束点对应的应变，εe2=10εe1；εe3为与钢材抗拉强度极限对应的应变，εe3=100εe1。

钢筋的应力-应变关系采用线性-完全塑性模型［9］，如图5(b）所示，即：

式中：εs为钢筋应变；εy为钢筋屈服应变，εy=fy/Es；Es为钢筋的弹性模量，取2.0×105MPa。

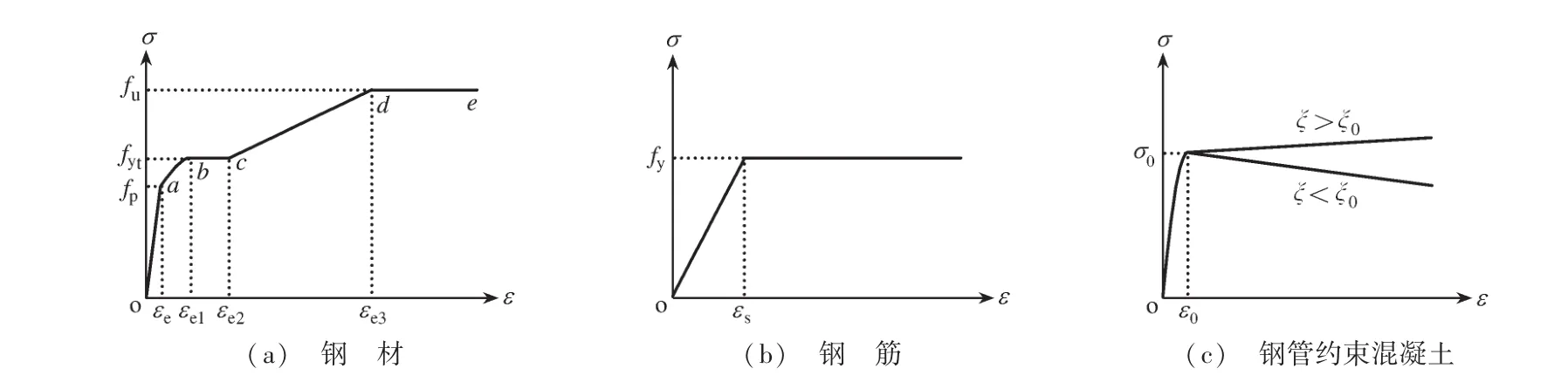
图5 材料本构关系Fig.5 Constitutive relationship of the materials

混凝土采用文献［8］中圆型钢管混凝土核心混凝土的应力-应变关系模型，如图5(c）所示，即：

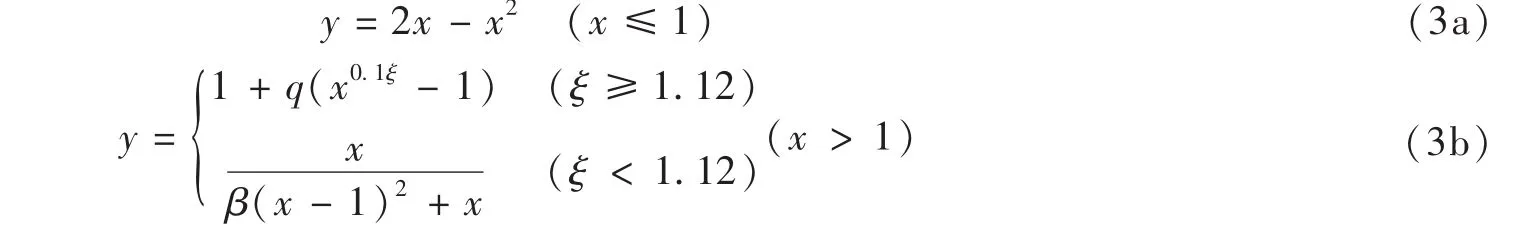
式中：σ，ε为混凝土压应力和压应变；σ0，ε0为混凝土峰值压应力和峰值压应变；x=ε/ε0， y=σ/σ0；ξ为钢管混凝土的约束效应系数ξ=Astfyt/Acfck；fyt，Ast为钢管的屈服强度和截面面积；fck，Ac为混凝土的标准抗压强度和截面面积。

纤维模型法将钢管的受力与对混凝土的约束效应分开考虑，属于考虑横向约束的一维应力分析。与有限元法相比(三维应力分析），计算简便。

2.1.3简化计算方法 前面两种方法适用于研究钢管钢筋混凝土构件的荷载-变形过程及构件的受力机理，由于计算比较复杂，不便于工程设计使用。为此，需要研究适于工程应用的简化承载力计算方法。虽然目前有钢筋混凝土和钢管混凝土专门的设计规范，但这些规范中的方法不能直接用于钢管钢筋混凝土承载力的计算。考虑到以往在嵌岩桩设计中通常忽略钢套管的作用而按钢筋混凝土构件设计，因此钢管钢筋混凝土构件承载力的计算方法借鉴钢筋混凝土构件承载力的计算方法比较合适。

图6 钢管钢筋混凝土柱简化计算模型Fig.6 Simplified calculation model of reinforced concrete column covered with steel tube

《水运工程混凝土结构设计规范》(JTS 151-2011［10］给出了圆形截面钢筋混凝土构件承载力的计算方法，公式是在理论分析的基础上经简化得到的，即当沿圆周均匀分布的钢筋不少于6根时，将钢筋连续化为同面积的钢环。对于圆形截面钢管钢筋混凝土构件，与普通钢筋混凝土构件不同的是，混凝土受到钢管的约束作用，同时钢管也直接参与受力。所以，理论上可将钢管视为钢筋的作用，而另将混凝土视为约束混凝土。即简化后的钢管钢筋混凝土按双钢筋考虑，混凝土按约束混凝土的强度计算(图6）。计算式为

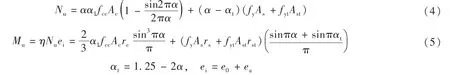
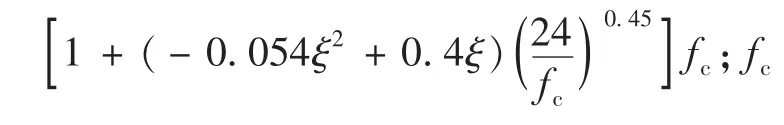
式中：φ为稳定系数，按文献［9］取值。

2.2 理论分析结果与试验结果比较

采用实测的材料性能，按有限元法和纤维模型法对钢管钢筋混凝土构件的荷载-变形进行计算，计算结果及试验得到的试件荷载-变形曲线示于图7中。除初始偏心距e0外，计算中考虑挠度f的影响。由图7可见，按有限元计算的荷载-变形曲线均低于试验测得的荷载-变形曲线，而纤维模型法的计算结果与试验结果比较接近，由此可见，复杂的分析方法并不一定得到更为准确的结果。实际上，模型过于复杂会导致材料参数过多，而材料参数具有不确定性，这种不确定性的叠加会导致计算结果的不确定性增加，可靠度指标降低。

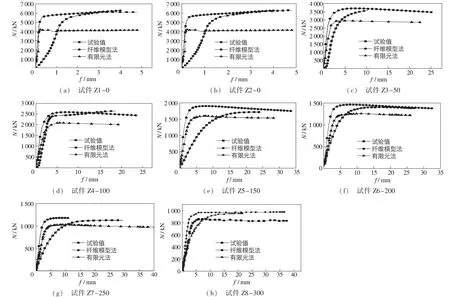
图7 试件荷载-变形曲线Fig.7 Load versus deformation relationship of the specimens

取构件荷载-变形曲线上的最大点作为构件的最大承载力，图8给出了试件的N-M关系曲线，表3给出了按有限元法、纤维模型法和本文提出的简化方法计算的承载力与试验承载力的比值。由图8和表3可见：试验值比3种数值模拟方法计算的结果偏大，这是因为理论计算方法都有一定的可靠度指标；具体来说，与试验结果相比，有限元法计算的承载力偏低，纤维模型法计算的承载力稍大，本文提出的简化计算方法与试验结果接近。因此，本文提出的钢管钢筋混凝土构件承载力的简化计算方法是可行的。

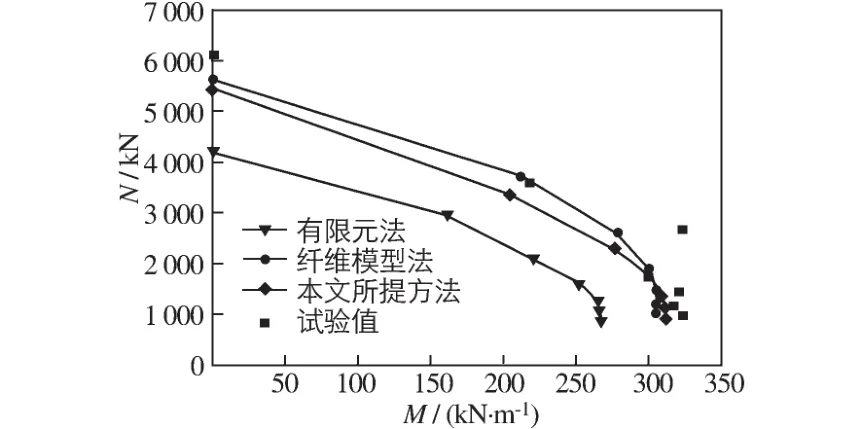
图8 试件N-M关系曲线Fig.8 N-M relationship of the specimens

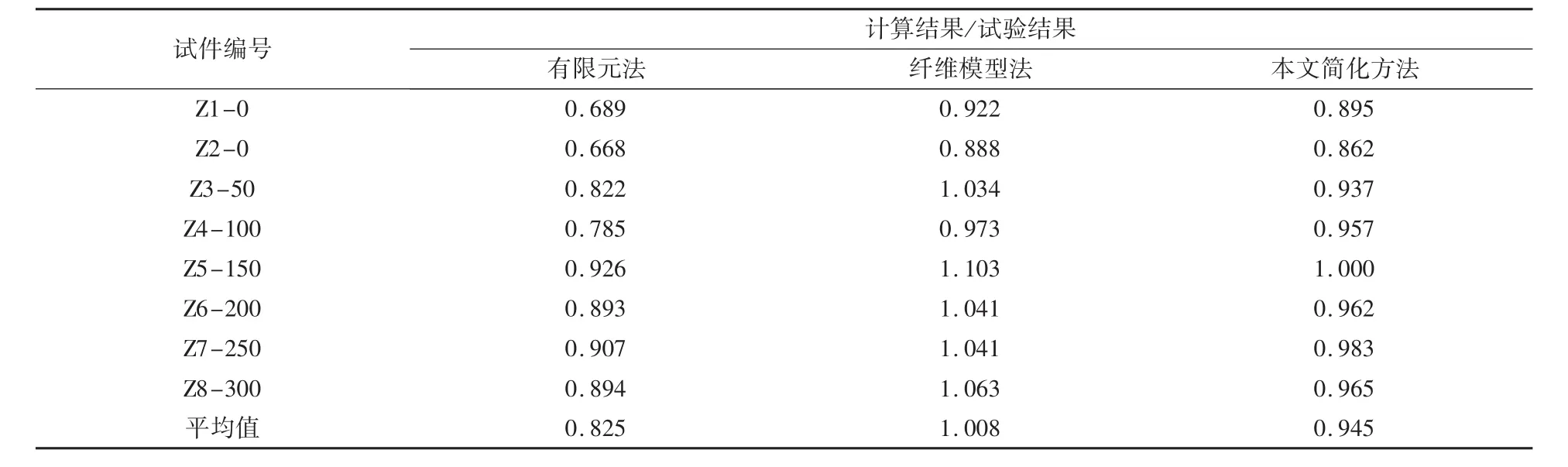
表3 3种方法计算结果与试验结果的比较Tab.3 Comparison between the results of calculation and experiment

3 结 语

本文对圆形截面钢管钢筋混凝土构件的承载力进行了试验研究和理论分析。研究得出如下结论：

(1）计算圆形截面钢管钢筋混凝土构件承载力时，可将圆形截面钢管钢筋混凝土构件等效为双层钢筋约束混凝土构件进行计算；

(2）钢管钢筋混凝土构件中的双层钢筋约束作用能够延缓核心混凝土的破坏，使钢管钢筋混凝土构件表现出极高的变形能力；

(3）本文提出的圆形截面钢管钢筋混凝土构件承载力简化计算方法计算简单，精度较高，适于工程应用。

［1］舒赣平，刘小萤，缪巍.配筋圆钢管混凝土轴心受压短柱试验研究与承载力分析［J］.工业建筑，2010，40(4）：100-106.(SHU Gan-ping，LIU Xiao-ying，MIAO Wei.Experimental research and bearing capacity analysis of axial compressive reinforced concrete-filled steel tube short column［J］.Industrial Construction，2010，40(4）：100-106.(in Chinese））

［2］韩金生，董毓利，徐赵东，等.配筋钢管混凝土柱抗压性能［J］.土木建筑与环境工程，2009，31(3）：11-17.(HAN Jinsheng，DONG Yu-li，XU Zhao-dong，et al.Analysis of axial compression performance for reinforced concrete-filled tubular steel［J］.Journal of Civil，Architectural&Environmental Engineering，2009，31(3）：11-17.(in Chinese））

［3］侯宇颖.配筋钢管混凝土短柱受力性能分析［J］.建筑设计管理，2010，27(12）：46-48.(HOU Yu-ying.Mechanical analysis of reinforced concrete-filled steel tube［J］.Architecture Design Management，2010，27(12）：46-48.(in Chinese））

［4］刘朝，赵均海，王娟，等.配筋圆钢管混凝土短柱轴压承载力分析［J］.建筑科学与工程学报，2011，28(4）：92-96. (LIU Zhao，ZHAO Jun-hai，WANG Juan，et al.Analysis of axial bearing capacity of reinforced concrete-filled circular steel tube short columns［J］.Journal of Architecture and Civil Engineering，2011，28(4）：92-96.(in Chinese））

［5］魏华，王海军.配筋圆钢管混凝土柱承载力的研究［J］.哈尔滨工业大学学报，2007，39(2）：70-73.(WEI Hua，WANG Hai-jun.Investigation on strength of concrete-filled circular steel tubular columns［J］.Journal of Harbin Institute Technology，2007，39(2）：70-73.(in Chinese））

［6］王頠，瞿伟廉.钢管混凝土弹塑性极限承载力研究现状［J］.华中科技大学学报：城市科学版，2004(2）：44-46. (WANG Wei，QU Wei-lian.State of the art of elastic-plastic ultimate loads of concrete filled steel tube［J］.Journal of Huazhong University of Science and Technology(Urban Science Edition），2004(2）：44-46.(in Chinese））

［7］WANG Juan，ZHAO Jun-hai，WU Sai，et al.Axial bearing capacity of steel reinforced concrete short column with double circular steel tubes［J］.Advanced Materials Research，2013，721：720-725.

［8］韩林海.钢管混凝土结构-理论与实践［M］.2版.北京：科学出版社，2004.(HAN Lin-hai.Structure of concrete filled steel tube：Theory and Practice［M］.2nd ed.Beijing：Science Press，2004.(in Chinese））

［9］GB 50017-2003，钢结构设计规范［S］.(GB 50017-2003，Code for design of steel structures［S］.(in Chinese））

［10］JTS 151-2011，水运工程混凝土结构设计规范［S］.(JTS 151-2011，Design code for concrete structures of port and waterway engineering［S］.(in Chinese））

Calculation method for load-carrying capacity of circular reinforced concrete members covered with steel tube

WANG Ting-wei1，GONG Jin-xin1，WU Zhi-liang2，ZHU Xiao-yu1
(1.Faculty of Infrastructure Engineering，Dalian Uniυersity of Technology，Dalian 116024，China；2.CCCC Third Harbor Consultants Company Limited，Shanghai 200032，China）

Axial and eccentric compression experiments are carried out on 8 circular reinforced concrete specimens covered with steel tube，and the finite element method and the fiber model method are used to calculate the loadcarrying capacity of the specimens.Based on the experimental and theoretical analysis，a simplified calculation method of the load-carrying capacity for this kind of member is proposed in the study.The analysis indicate that the finite element method result is relatively small，and that the results of the load-carrying capacity of the specimens calculated by the fiber model method agree well with the experimental results.The circular reinforced concrete members covered with steel tube present the characteristics of both the reinforced concrete and concrete filled steel tube members，showing higher load-carrying capacity and greater deformability.The load-carrying capacity of circular reinforced concrete members covered with steel tube can be calculated by the method of the reinforced concrete member with the confined concrete.The load-carrying capacity of the circular reinforced concrete members covered with steel tube calculated by the simplified method is in good agreement with the experimental results.

reinforced concrete members covered with steel tube；circular section；load-carrying capacity；finite element method；fiber model method

TU375；TU473.11 文献标心码：A

1009-640X(2014）03-0018-08

2013-11-18

国家自然科学基金资助项目(51278081）

王廷伟(1990-），男，河北张家口人，硕士研究生，主要从事建筑结构设计和抗震研究。E-mail：kelvinwangting@163.com