基于IOWA算子的安徽省城镇居民人均消费支出的组合预测

胡海翔，杨桂元

（安徽财经大学统计与数学应用学院，安徽蚌埠 233030）

一、引言

改革开放以来，我国经济一直处于上升阶段，同时消费、投资和出口是拉动经济增长的三驾马车。我国一直以消费刺激经济增长为主，如何刺激居民消费，扩大国内消费，从而拉动经济，是政府关注的大事。同时在居民消费中主要以城镇居民消费为主，所以对城镇居民人均消费支出的预测，从而为政府制定相关的政策或者分析城镇消费市场具有重要意义。

目前国内外有很多预测方法包括回归分析法、时间序列分析法等等，但是我们发现很多单一的预测方法存在着很多的缺陷和不足，所以我们考虑采用组合预测的方法进行预测。组合预测是1969年由Bates和Granger提出的，是将各项单项预测看作代表或包含不同信息的片段，通过信息的集成分散单项预测的不确定性和减少总体不确定性，从而提高预测精度[1]。陈华友和刘春林通过引进诱导有序加权算术平均（IOWA）算子，提出了以误差平方和为准则新的组合预测模型，给出了IOWA权系数的确定的数学规划方法[2]。陈华友、陈启明和李洪岩以最大绝对误差最小化的组合预测模型为例引进有序加权平均（OWA）算子，给出了其线性规划的求解方法[3]。肖祎平、刘新卫和张威运用ARIMA模型、GM（1，1）模型和RBF神经网络模型以及非负权重最优组合预测模型对中国银行的收盘价进行分析和预测，取得了很好的效果[4]。李伟和董梅生根据1995—2007年安徽省农民收入和消费的数据采用偏最小二乘回归方法得出农民收入对消费水平的影响很大，得出了农民收入和消费存在着较高的相关关系[5]。

二、模型的选择

当前已知的组合预测方法都是按照每项单项预测方法预测的不同精度来赋予大小不同的加权平均系数，同时传统组合预测方法认为同一项单项预测方法在样本区间上各个时点的加权平均系数是不变的。然而在样本区间的不同时点上对于同一个单项预测方法的准确度是不相同的，即同一单项预测方法在这个时点上对样本的预测精度较高，然而在另一时点上这一单项预测方法可能预测的精度比较差。所以现在已知的传统组合预测方法预测现实问题会出现预测精度下降的问题。陈华友引进诱导有序加权算术平均算子（IOWA），即在组合预测中可以根据样本区间不同时点上每项单项预测方法的预测精度的高低来赋予不同的权重，从而提高了整个组合预测的精度，同时以误差平方和最小为判定准则进入组合预测方法中。

（一）传统的以误差平方和为准则的组合预测

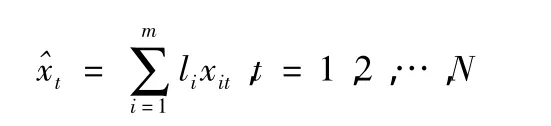
则称xt为对实际观察值xt加权算术平均的组合预测值。

设et为第t时刻的组合预测值与相应的实际值之间的误差，则

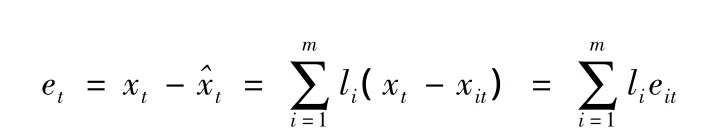
其中eit=xt－xit为第i种预测方法第t时刻预测值与相应的实际值之间的误差，i=1，2，…，m，t=1，2，…，N，所以N期总的组合预测误差平方和为

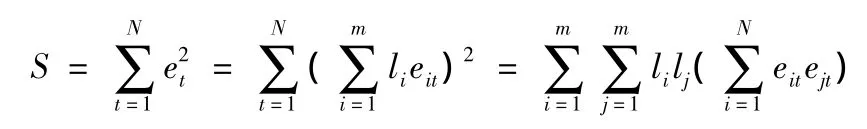
因此以误差平方和为准则的加权算术平均组合预测模型如下：

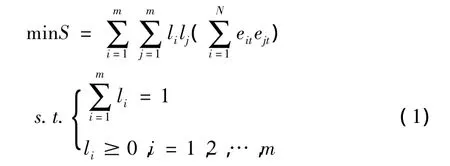
由模型（1）的最优解即为加权算术平均组合预测模型的权重。

（二）三个概念

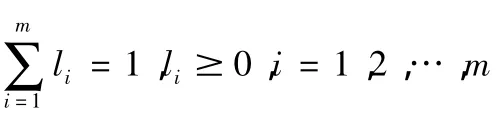
定义2 设＜v1，a1＞，＜v2，a2＞，…，＜vm，am＞为m个二维数组，令

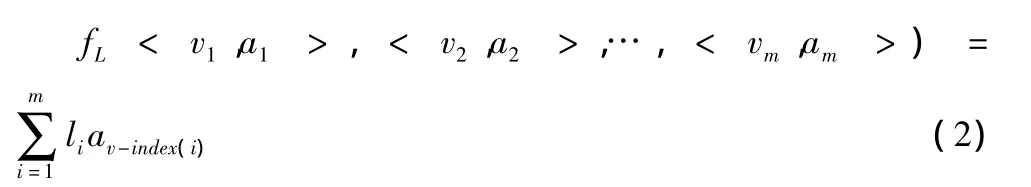
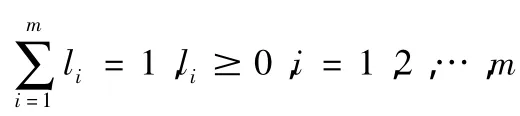
则bit表示的是第i种预测方法在第t时刻的预测精度，且bit∈[0，1]。

（三）模型的建立

在此我们把定义3中的预测精度vit看成预测值xit的诱导值，这样m种单项预测方法在第t时刻的预测精度和其对应的在样本区间的预测值构成了m个二维数组＜v1t，x1t＞，＜v2t，x2t＞，…，＜ vmt，xmt＞。

令L=（l1，l2，…，lm）T为加权向量，根据定义2中的式子，可以得到

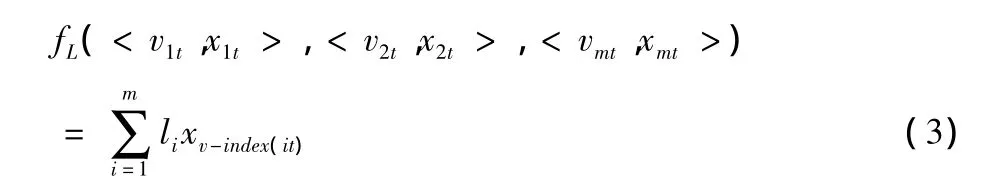
其中v－index（it）是第i个大的预测精度的下标。我们称（3）式是将m种单项预测方法在第t时刻的预测精度序列v1t，v2t，…，vm t按从大到小顺序排列所形成的组合预测值。

于是N期总的组合预测误差平方和S

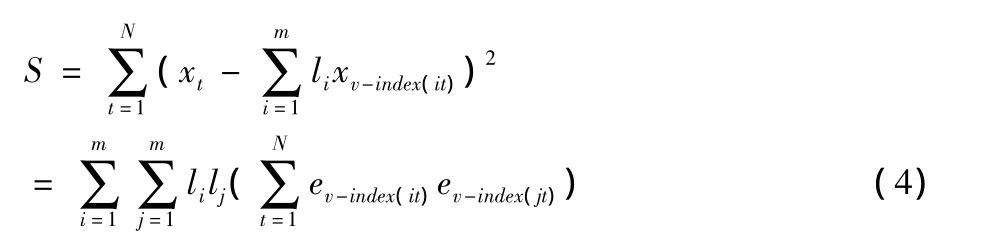
其中令ev－index（it）=xt－ xv－index（it），故以误差平方和最小为准则的基于IOWA算子组合预测模型如下：

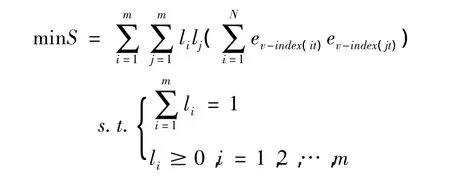
三、实证分析

本文选取的是1992－2012年的安徽省城镇居民人均消费支出进行预测分析，共21个样本。并且用多元线性回归与时间序列的组合模型预测、ARIMA模型预测、GM（1，1）模型预测三种单项预测方法进行分析。数据来源于安徽省统计年鉴。

（一）多元线性回归与时间序列的组合模型预测

1.模型原理

多元回归预测是分析应变量和自变量是否存在着一定的长期关系，即自变量和因变量之间是否存在着线性相关关系，以及各自变量之间对因变量的影响程度如何。

设Y是因变量，X1、X2、…、Xn是自变量，则模型可写成

Y=α+β1X1+β2X2+…+βn Xn+ε

其中i=1，2，…，n，ε 为随机误差项，且 ε～ N（0，σ2）

2.模型检验和预测

首先此模型选取的数据样本是1992－2012年的安徽省城镇居民人均消费支出（Y）、城镇居民家庭人均收入（X1）、居民消费价格指数（X2）和城镇居民家庭恩格尔系数（X3）。Y、X1、X2和X3的值如表1所示。

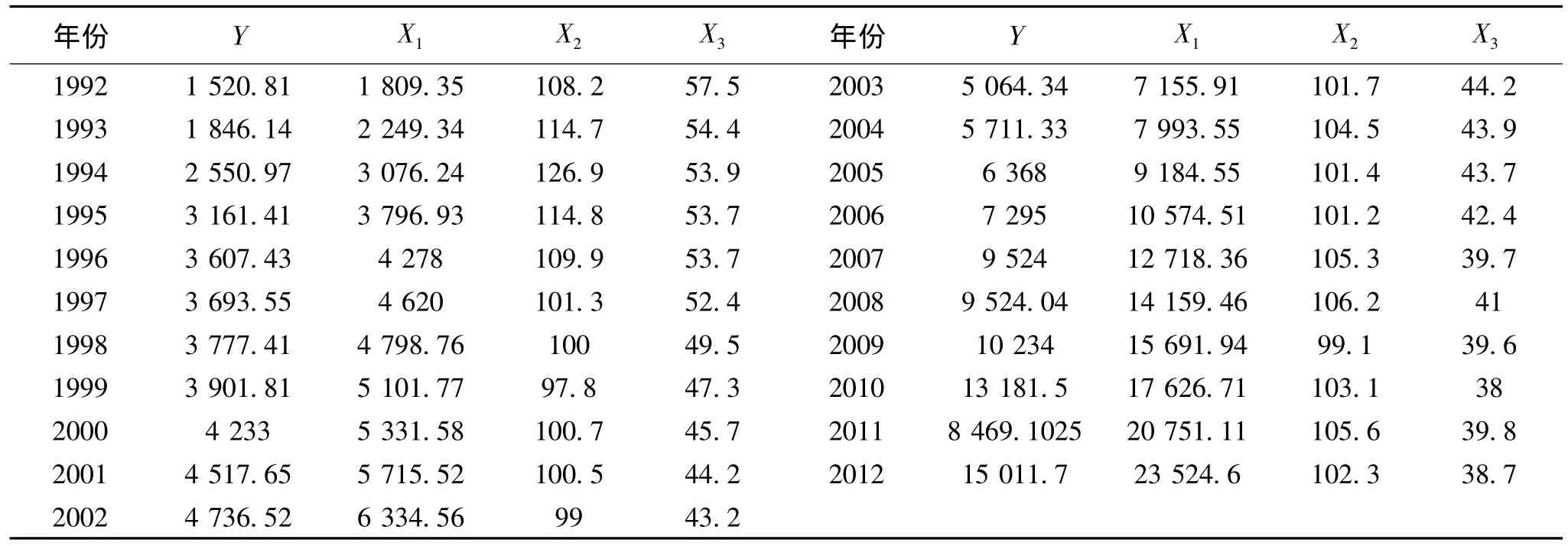
表1 选取的数据样本的值

首先对样本Y、X1、X2和X3进行最小二乘估计，再剔除不显著变量得回归方程，但是观看DW值为1.55表示存在序列相关，为此我们引入AR（1）和MA（1），得到的方程如下：

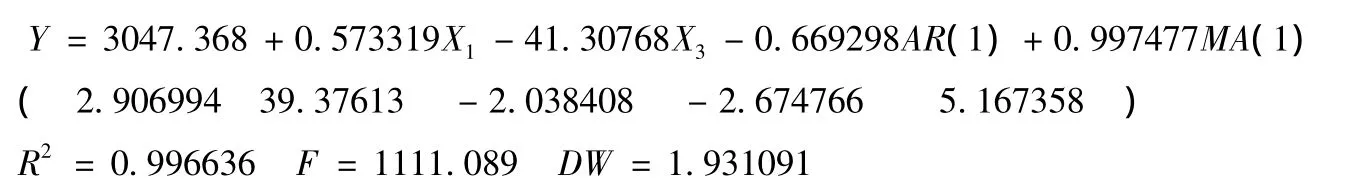
可以看出回归方程拟合的比较好，可以用该方程进行预测，预测结果见表2。

（二）ARIMA模型预测

1.模型原理

自回归求积移动平均模型也就是ARIMA模型，是将非平稳时间序列转换为平稳时间序列，然后将因变量对它的滞后值及随机误差进行回归所建立的模型。

设Yt是被解释变量，ut是随机扰动项，如果Yt被它的p个滞后变量和ut的q个滞后变量所解释，模型可写成

上式称为p阶自回归与q阶移动平均模型，记为ARMA（p，q）。如果非平稳时间序列经过d次差分后才变成平稳的，那么该时间序列模型变为自回归求积移动平均模型，记为 ARIMA（p，d，q）。

2.模型的识别、检验和预测

首先对21个数据进行ADF检验，确定d值。直接对Y进行ADF检验为平稳时间序列，在显著性水平为5%的时候为平稳序列。因此d的值为0。

其次我们利用自相关函数ACF和偏自相关函数PACF确定p、q的值。用Eviews软件处理得到自相关函数ACF和偏自相关函数PACF图像见表3.经过反复试验将p，q的值定为2和1能够取得很好的拟合效果（拟合优度R方为0.982314.AIC和SC信息值分别为15.60152和15.8）且利用residual tests中correlogram－Q－statistics检验发现残差序列不相关，属于白噪声序列。因此可以用ARIMA（2，0，1）模型进行预测，预测值见表2。

（三）GM（1，1）模型预测

1.模型原理

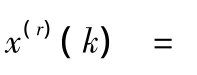
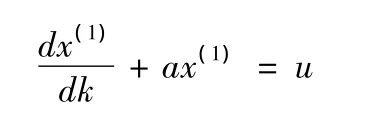
其解的离散形式为

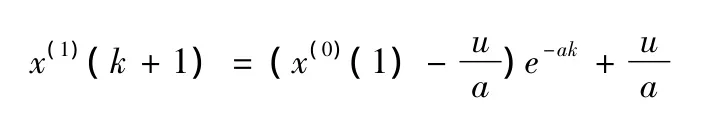
模型中的参数可用最小二乘确定

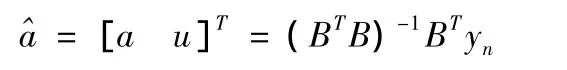
式中

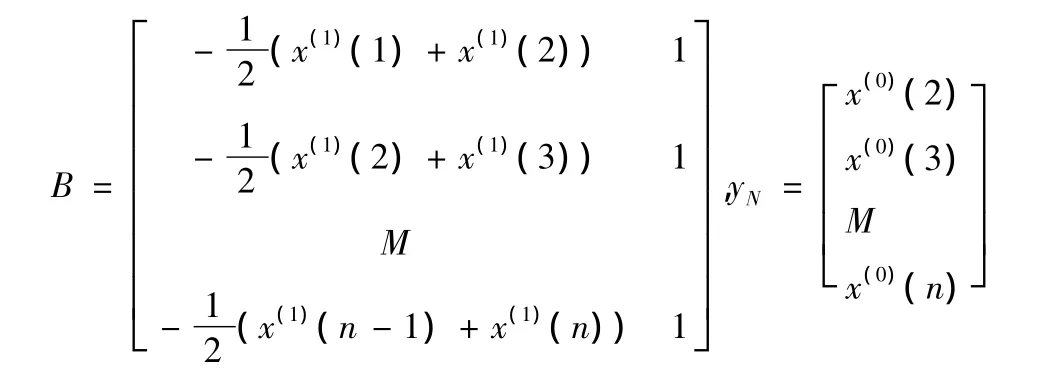
确定参数a和u后按此模型递推，可以得到预测的累加数列，再累减可得到预测值。然后对序列进行残差合格性检验、关联度合格性检验及小误差概率合格性检验，结合精度检验等级参照表判定所建立模型的优劣，通过检验即可进行预测。

2.建立模型与预测

首先对原始数列进行级比检验。根据公式σ（k）=x（k－1）/x（k）对原始序列计算，得到级比序列σ=（0.823778，0.723701，…，0.878082），令n=5，再根据公式σ（k）∈（，）得到可容覆盖为（0.67032，1.491825），由于都落在可容覆盖中，可以建立灰色预测模型GM（1，1）.

其次建立GM（1，1）模型。由Matalab软件可得预测模型为

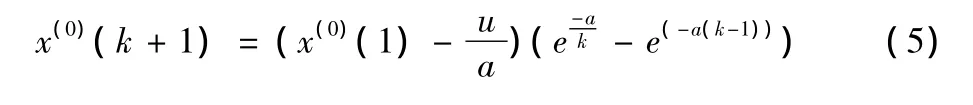
其中a=－0.1023，b=1732.5284。根据公式（5）进行拟合，拟合的平均相对误差为0.2043%，拟合精度较高。因此预测结果见表2。

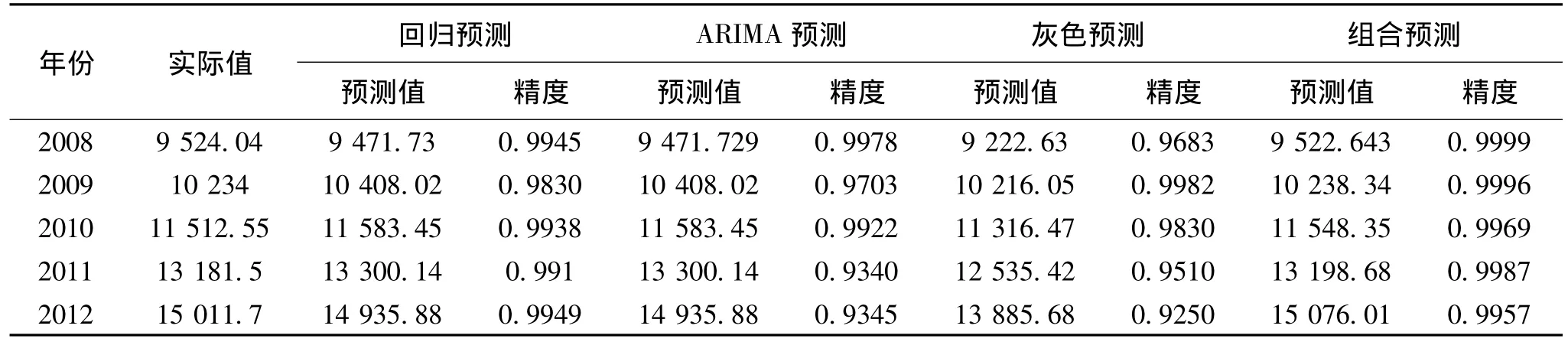
表2 各单项预测和组合预测的结果

（四）组合预测

根据以上各时点上的各单项预测法的预测精度为诱导值，并且预测精度按从大到小排列，对各时点的各种单项预测法的预测值进行有序加权平均，并且以误差平方和最小为准则，用Lingo软件求解，得最优权系数向量L=（0.8026，0.1648，0.0326），即对于单项预测法预测精度最高的赋与0.8026，对于次高的赋予0.1648，最低的赋予0.0326。从表2中可以看出组合预测的方法的预测精度都是最高的，显著提高了预测精度。整体上比每一单项预测方法的预测精度高。根据得到的权重向量，因此组合预测的预测模型为

fL=0.8026xb－index（1t）+0.1648xb－index（2t）+0.00326xb－index（3t）

我们根据以上计算出来的权重计算每项单项预测方法的各时期平均权重作为未来时期的各个单项预测方法的权重，然后计算组合预测值作为未来的预测值。预测值见表3。

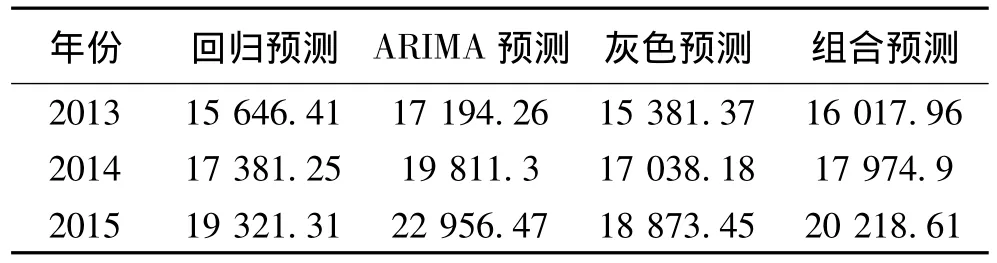
表3 2013－2015年的组合预测结果

从表3中可以看出，2012年以后各年的城镇消费支出确实在逐年增大，拉动经济的增长。这与政府刺激内需，扩大我国居民消费支出，拉动外需，从而带动经济稳定快速的增长政策目标一致。在全省经济增速放缓的情况下，我们应该扩大居民消费支出，特别是城镇居民消费，从而拉动内需，带动经济稳定快速的增长。

四、总结

影响城镇居民人均消费支出的变化的因素众多，单一的预测方法虽不能全面的描述这一变化的具体趋势，但这些预测方法能从不同的角度来预测人均消费支出额;而组合预测是将不同的预测方法进行适当的组合，通过综合利用各种预测方法所提供的信息，尽可能提高预测精度。本文通过用1992－2012年的安徽省城镇居民人均消费支出进行预测分析来说明基于IOWA组合预测方法的预测精度，而实践证明，基于IOWA组合预测确实能取得优于各个单项预测的效果，提高了预测的精度。

安徽省城镇居民人均消费支出的实证结果可以推广到全国范围内，可以运用基于IOWA组合预测方法对全国城镇居民未来几年的人均消费支出做出预测。预测的结果可以为政府在接下来几年里实施刺激国内消费的措施与方针提供依据和数据支持。

[1]Bates J M，Granger C WJ.Combination of forecasts[J].Operations Research Quarterly，1969，20（4）：451 －468.

[2]陈华友，刘春林.基于IOWA算子的组合预测方法[J].预测，2003，22（6）：61－65.

[3]陈华友，陈启明，李洪岩.一类基于OWA算子的组合预测模型及其性质[J].运筹与管理，2006，（12）：34－40.

[4]肖祎平，刘新卫，张威.基于非负权重最优组合预测的股价预测研究[J].统计与决策，2013，（18）：142－145.

[5]李伟，董梅生.安徽省农民消费水平和收入水平的关系——基于偏最小二乘法的分析[J].商场现代化，2009，（22）：66－68.

[6]安徽统计年鉴——2013[Z].北京：中国统计出版社，2013.