轿车系统的模拟装置与动态分析

杨咸启，杨 琪，鲍 婕

(黄山学院 机电工程学院，安徽 黄山 245041）

1 概 述

研究发现，轿车乘坐舒适性及操纵安全性与轿车悬挂系统的关系密切。理想的悬挂系统不仅能使车随路面起伏而上下运动，并能借此使整个车身在前进过程中尽量保持水平。还能随车速、路况、运动方式的变化做出适当、灵敏的反应。它能使轮胎与路面贴合，保持适当的角度，从而使轿车的动力性能、制动性能以及转向性能等得到保证。本文设计一种轿车悬挂机构模拟装置，用来模拟汽车在竖直方向的振动。当调整轿车悬挂系统参数时，可以评价参数调整对轿车系统振动造成的影响。

2 轿车系统模型

实际轿车的振动是很复杂的，影响振动的因素很多，这里考虑主要因素，而略去一些次要因素，将系统简化和抽象为动力学模型。建立合理的汽车振动的动力学模型，对于分析和计算的结果的准确性是至关重要的。[1]本文考虑轿车在随机不平路面上行驶时，路面的随机输入对人产生的响应。

轿车在路面上的行驶产生振动，测出其在竖直方向上的位移、速度，为了保证模拟装置的尺寸及其他参数与轿车的实际情况成一定的比例，这里采用如下方法。

1.设计的装置缩小比例为1：5；

2.汽车内部质量集中设置，轮胎弹性采用空气弹簧模拟；

3.地面变化采用凸轮轮廓进行模拟。

设计的轿车系统模拟装置简图如图1所示。该系统的理论分析模型简化为8自由度运动模型[2]，如图2所示。8个自由度分别是：簧载质量质心处的垂直位移Zc、前面非簧载质量质心处的垂直位移Z1、后面非簧载质量质心处的垂直位移Z2、人-椅的系统质心处的垂直位移Zp、簧载质量横向角振动的角位移ξ、簧载质量纵向角振动的角位移φ、前排非簧载质量横向角振动的

图1 轿车系统模拟装置

角位移θ1、后排非簧载质量横向角振动的角位移θ2。

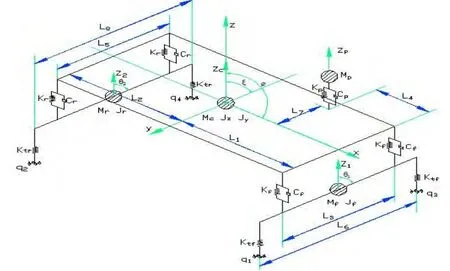
图2 轿车系统计算模型

轿车系统的运动微分方程组的矩阵的形式为[2-5]：

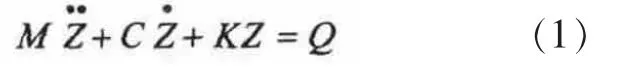
其中，C为阻尼矩阵，K为刚度矩阵，M为质量矩阵，Q为激励矩阵。

3 模拟路面模型

为了更好地描述路面的状况，同时又考虑到计算的可行性，采用模拟函数描述路面激励。在系统分析中，路面激励起着重要的作用，它的准确性很大程度上影响模拟的真实性。本文采用的路面激励为多次谐波函数叠加函数：

路面的输入就能够粗略地描述如图3所示。

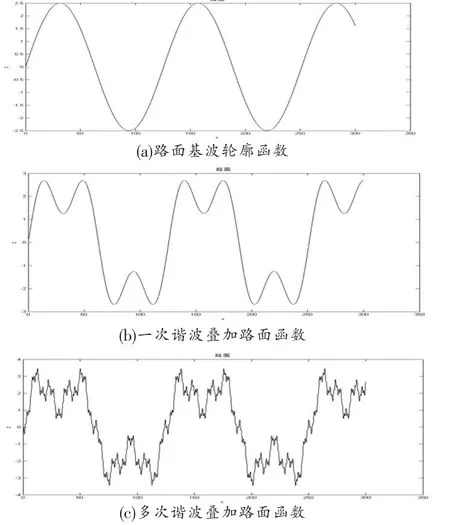
图3

4 模拟结果分析

轿车在不同的路面上行驶振动的差别往往比系统参数的改变要大，路面模拟函数对振动的影响十分明显。表1给出5种路面条件，采用龙格-库塔（Runge-Kutta）法[5]求解方程（1），得到人-椅系统（Mp）、中间簧载部分（Mc）和前、后非簧载部分（Mf、Mr）的位移和速度模拟结果，如图4所示。

表1 5种路面参数

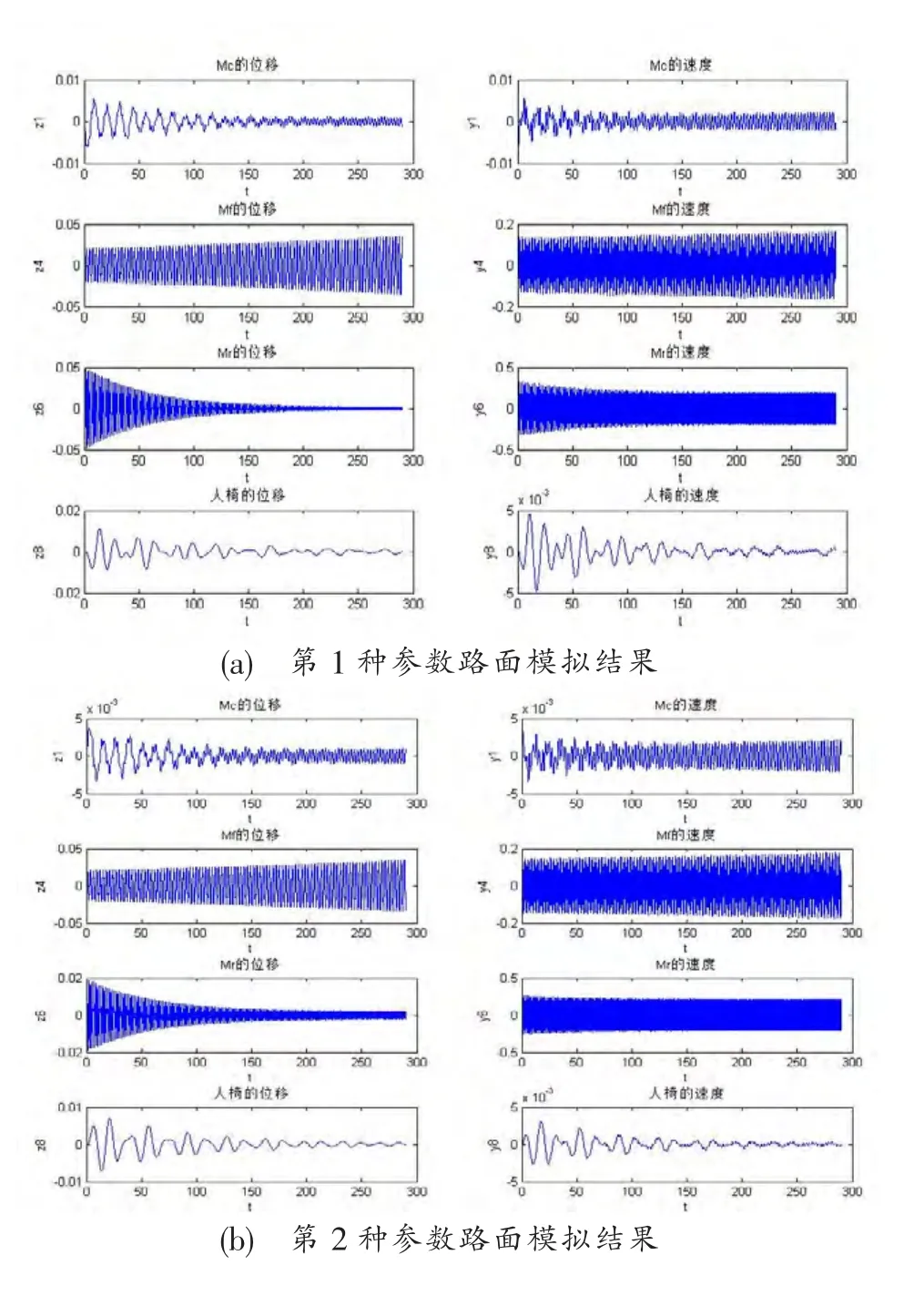
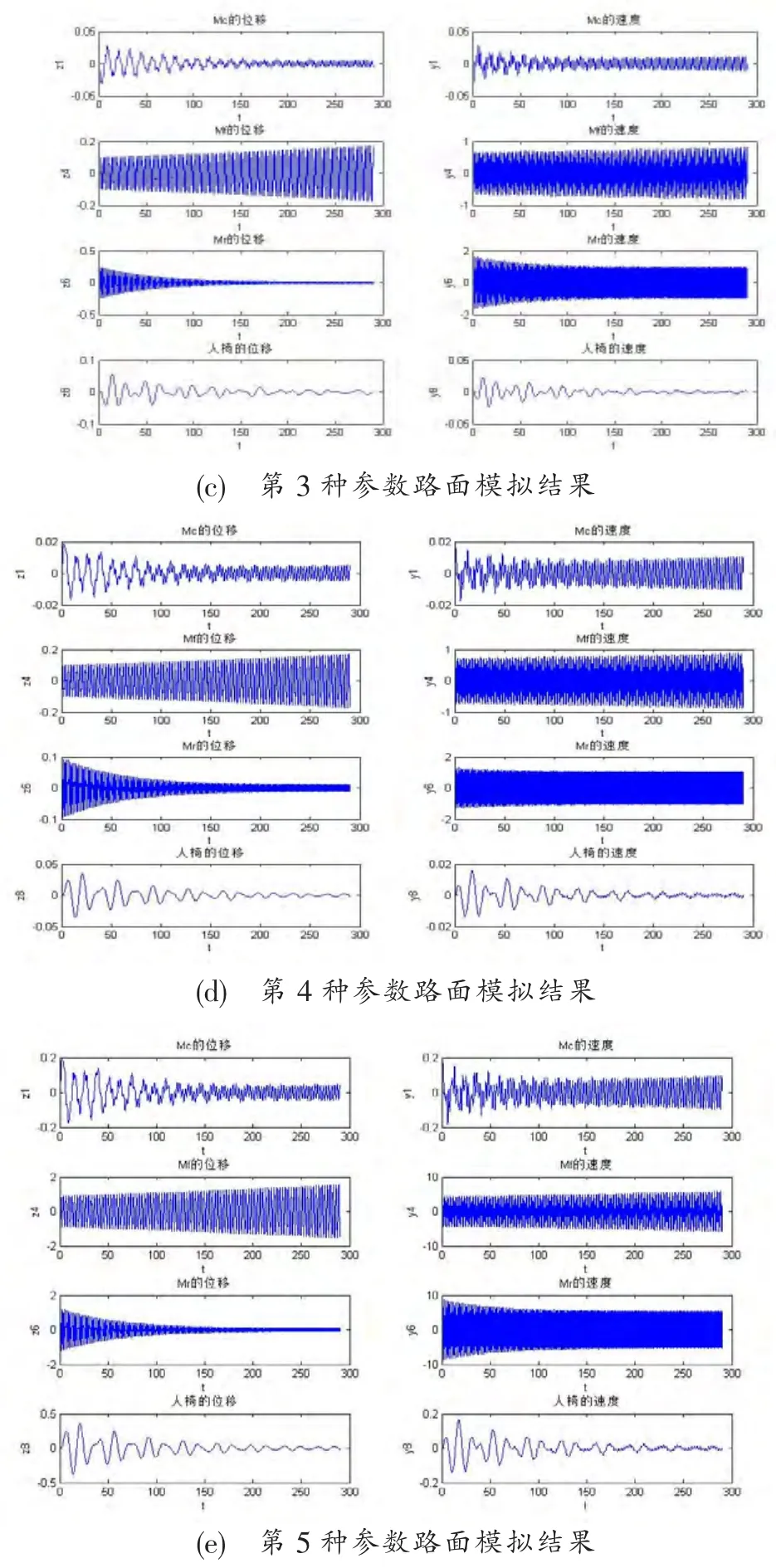
图4

5 结 论

通过5种参数路面条件下轿车的位移和速度的模拟结果，得出如下结论。

1.轿车的人-椅系统、簧载质量系统的振动在行驶初始期振动很强烈，随后逐渐趋于平稳。

2.轿车系统的角速度系数具有较大的影响，轿车的人-椅系统的角速度系数大振动振幅大，反之振动的振幅小。

3.当系统角速度系数不变的情况下，轿车系统振幅系数影响显著，振幅系数大振动就会大。

4.路面模型5的轿车人-椅系统的振幅值比在路面模型4的振幅值小很多。由此可以看出，并不是路面的不平度越高，轿车行驶时的振动就越剧烈，轿车在不同路面上的振动与其行驶的速度等因素也有一定关系。

[1]陆正煜.汽车独立悬架系统运动学与动力特性的研究与其优化设计[D].北京：清华大学,1985：5-19.

[2]丁玉庆.汽车振动系统的简化及数学模型的建立[J].南京理工大学学报，2001,25(4)：391-394.

[3]师汉民.机械振动系统——分析、测试、建模、对策（上册）[M].武汉：华中理工大学出版社，1992：32-59.

[4]杨咸启,常宗瑜.机电工程控制基础[M].北京：国防工业出版社，2005：168-201.