Sawada-Kotera方程的两类尖孤立波解

李向正

（河南科技大学数学与统计学院，河南 洛阳 471023）

Sawada-Kotera方程的两类尖孤立波解

李向正

（河南科技大学数学与统计学院，河南 洛阳 471023）

用（G′／G）展开法构造出了 SK方程的两类尖孤波解。这两类孤波解都有尖峰或倒尖峰，且满足Rankine-Hugoniot条件和熵条件，是方程的弱解。

Sawada-Kotera方程；尖孤波解；Rankine-Hugoniot条件；（G′／G）展开法；弱解

0 引言

研究数学物理方程的中心内容是求各类问题的解并研究解的性质，使人们对其所描述的自然现象或过程能有更深入的认识。间断性（或奇异性）在自然现象中广泛存在，如流体动力学中的溃坝，空气动力学中的激波，广义相对论中的黑洞等［1］。非线性发展方程是近年来数学物理工作者研究的热点，其弱解一般具有间断性（或奇异性），对于特定的自然现象，用弱解来描述或刻画更符合实际。弱解的存在性可用算子分解方法证明，也可用位势井理论和紧致性方法证明［2－3］。根据压缩映像原理用伽罗金逼近法可证明弱解的存在性和唯一性［4］。已有的文献较多地集中于弱解的存在性或唯一性的证明［2－5］，但弱解的解法或构造方法很少见文献报道。

本文研究Sawada-Kotera方程（SK方程）［6］

的尖孤立波解。SK方程可用于共形场理论，二维量子引力规范场理论和非线性科学中的Liouville方程的守恒流［7］。文献［6］用双曲正切函数展开法得到了SK方程的一些精确解。SK方程的Ham iltonian结构，Lax对，Bäck lund变换已被研究过［8］。文献［9］借助计算机代数系统获得了SK方程的孤波解和振荡孤波解。文献［10］利用SK方程的Bäcklund变换，从一个已知解出发得到方程的一些精确解。文献［11］应用改进的F展开法获得了SK方程的孤波解和三角函数解。文献［12］用指数函数法获得了SK方程广义孤立波解和周期解。但文献［6－12］均未考虑SK方程的尖孤立波解及其构造方法，因而本文主要解决这一问题。

1 SK方程的尖孤立波解

方程（1）可写成守恒律形式

方程（1）的尖孤立波解满足的边界条件为：

证明 利用洛比达法则及方程（2）可得：

下面用（G′／G）展开法［13－14］求解方程（1）。设方程（1）的行波解为：

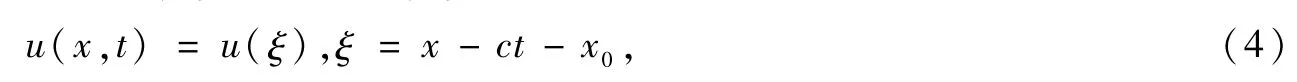
其中，常数c表示波速；x0为常数。将式（4）代入方程（1），而后关于ξ积分一次，根据边界条件（3），可设积分常数为零，得

此处，要求方程（1）的弱解u（x，t）＝u（ξ）满足对称性条件

考虑方程（5）中u3，uu″和u（4）的齐次平衡［13－16］，3m＝2m＋2＝m＋4，得平衡数m＝2，于是设方程（5）的解可表示为：

其中，a0、a2为待定常数；G＝G（ξ）满足二阶线性常微分方程

其中，β为待定常数。特别地当β＜0时，

其中，ξ0、ξ1为常数。

将式（7）代入方程（5）的左端并利用方程（8），则方程（5）的左端化为（G′／G）的多项式，置多项式的系数为零，得到关于a0、a2、β和c的代数方程组，利用Mathematica（符号运算软件），解得该方程组的3组解，它们是：

第2类孤立波解u10～u12，当ξ1＞0时均有倒尖峰。根据定理1，解u10～u12也满足Rankine-Hugoniot条件，因而是方程（1）的弱解。由于熵条件成立，因而解u10～u12为方程（1）的物理解。u7～u12的物理解当ξ0＞0（ξ1＞0）时在间断曲线上有尖峰（倒尖峰）。据作者所知，这些解在以往文献中尚未报道。解u7的图形见图1（取a0＝2），解u10的图形见图2（取a0＝2）。

图1 相同相速c＝16／9下的孤立波u7，从上到下ξ0＝0，ξ0＝1／2，ξ0＝1，ξ0＝3／2

图2 相同相速c＝16／9下的孤立波u10，从下到上ξ1＝6／5，ξ1＝7／5，ξ1＝8／5，ξ1＝9／5

2 结论

SK方程的尖孤立波尚未见文献报道。本文首先给出了满足守恒律的非线性发展方程的行波解满足Rankine-Hugoniot条件的定理，而后利用（G′／G）展开法求出了SK方程的具有对称性的行波解，首次构造出了SK方程的两类尖孤立波解。这两类尖孤立波解的振幅均有限，满足Rankine-Hugoniot条件和熵条件，因而为SK方程的物理解。第1类尖孤立波解u7～u9，当ξ0＝0时对应于经典的光滑孤波解，因而比经典的孤波解更具有一般性。本文的工作拓展了（G′／G）展开法［13－14］的应用范围。另外，文献［1］认为尖孤立波可能是浅水波模型的一个一般性质，本文则从数学角度严格证明了具有尖孤立波解的方程必须满足的条件，即满足定理1的条件，边界条件（3）及对称性条件（6），依据这些条件即可扩展具有尖孤立波解的方程的类型。

致谢：本文得到王明亮教授的指导，在此表示感谢。

［1］ Liao S J.Two Kinds of Peaked Solitary Waves of the KdV，BBM and Boussinesq Equations［J］.Science China，2012，55（12）：2469－2475.

［2］ 谢永钦，马加磊，肖霞，等.一类非线性发展方程解的长时间行为［J］.湘潭大学学报：自然科学版，2012，34（1）：1－4.

［3］ 廖秋明，赵红星.一类具耗散项的非线性四阶波动方程的整体弱解及其渐近性质［J］.工程数学学报，2013，30（1）：59－66.

［4］ 夏子伦，曹文慧，杨文斌.一类非线性双曲型方程的弱解［J］.云南民族大学学报：自然科学版，2013，22（1）：48－53.

［5］ 李灵晓，李二强.时滞Cahn－Hilliard方程的孤立波解［J］.河南科技大学学报：自然科学版，2013，34（4）：88－90.

［6］ Abdul-Majid W.Abundant Solitons for Several Forms of the Fifth-order KdV Equation by Using the Tanh Method［J］. Applied Mathematics and Computation，2006，182：283－300.

［7］ 阮航宇.（2＋1）维Sawada-Kotera方程中两个Y周期孤子的相互作用［J］.物理学报，2004，53（6）：1617－1622.

［8］ He G L，Geng X G.An Extension of the Modified Sawada-Kotera Equation and Conservation Laws［J］.Chin Phys B，2012，21（7）：070205.

［9］ 李志斌，潘素起.广义五阶KdV方程的孤波解与孤子解［J］.物理学报，2001，50（3）：402－405.

［10］ 徐惠益.Sawada-Kotera方程的Bcklund变换及其精确解［J］.苏州大学学报：自然科学版，2005，21（1）：24－27.

［11］ 张平.关于一类五阶非线性发展方程的新精确解［J］.五邑大学学报：自然科学版，2008，22（1）：35－39.

［12］ 刘常福，戴正德.一类五阶非线性演化方程的广义孤立波解和周期解［J］.西南大学学报：自然科学版，2010，32（1）：1－4.

［13］ Wang M L，Li X Z，Zhang J L.The（G′／G）-expansion Method and Traveling Wave Solutions of Nonlinear Evolution Equations in Mathematical Physics［J］.Physics Letters A，2008，372（4）：417－423.

［14］ 李向正，张卫国，原三领.（G′／G）展开法的简化及Nagumo方程的有界行波解［J］.河南科技大学学报：自然科学版，2010，31（6）：18－81.

［15］ Wang M L.Solitary Wave Solutions for Variant Boussinesq Equations［J］.Phys Lett A，1995，199：169－172.

［16］ Li X Z，Wang M L.A Sub-ODE Method for Finding Exact Solutions of a Generalized KdV-mKdV Equation with Highorder Nonlinear Terms［J］.Physics Letters A，2007，361：115－118.

［17］ 胡国定.简明数学词典［M］.北京：科学出版社，2007：481.

O175.2

A

1672－6871（2014）02－0078－04

国家自然科学基金项目（10871129）；河南科技大学科研创新能力培育基金项目（2010CZ0016）；河南科技大学博士启动基金项目（09001562）

李向正（1972－），男，河南偃师人，副教授，博士，主要研究方向为非线性数学物理方程.

2013－09－25