基于数学广角视野的“鸡兔同笼”问题教学

■王钊

基于数学广角视野的“鸡兔同笼”问题教学

■王钊

【教学背景】

如果一个人站在十字路口，从理论上讲，朝东、南、西、北四个方向走，都是有可能的，也都有其合理性。但是，如果要联系他从哪里来，要到哪里去来重新进行思考，那么，就不是每一种可能都是合理的了。

前者就好比我们对纯文本的解读，单纯看“鸡兔同笼”问题，无论用什么策略解决这类问题都是合理的。但是，如果把这个文本放在特定的大环境下——数学广角视野中，从教学的整体出发，我们就会发现，并不是每一种“有理的”解读都是“合理的”。

很多教师已经尝试对“数学广角——鸡兔同笼”问题进行过研究，我听过的课中，有的老师把它上成“鸡兔同笼”问题的专题讲座；有的老师的课堂只有十来个思维活跃的学生追随，其他学生望而生畏；有的老师甚至在一节课中向学生传授用十几种方法来解决“鸡兔同笼”问题……这样的教学有悖于学生的认知规律，有违编者意图。因此，有必要对这个教学内容进行再研究，力求通过这样的教学达到数学广角应该达到的教学效果。

【课堂写真】

（出示：今有鸡兔同笼，从上面数，有8个头，从下面数，有26只脚。鸡和兔各有几只？）

师：我们先来猜测一下，到底有几只鸡，几只兔呢？（学生猜测并验证，教师随学生回答板书）

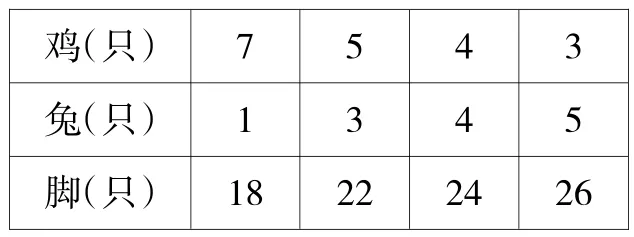
鸡（只） 7 5 4 3兔（只） 1 3 4 5脚（只） 18 22 24 26

师：刚才我们的这些猜测，其实就是对答案的一种假设。这种任意的假设可能符合题意也可能不符合题意。像7只鸡、1只兔这样的假设不符合题意，因为它们只有18只腿。能不能通过调整使腿数符合26只呢？

生：能。

师：请仔细观察，7只鸡1只兔，总脚数18只，比26只少。那么鸡、兔的只数应该向什么方向调整？

生1：应该减少鸡的只数，增加兔的只数，这样总脚数就会增加。

师：很有道理！究竟要怎样调整鸡兔的只数才符合26只脚的要求呢？把你的想法在小组里交流一下。（小组讨论）

生2：我把先鸡减少1只，兔增加1只，就有6只鸡2只兔，现在就有20只脚了；然后再把鸡减少1只，兔增加1只，就有5只鸡3只兔，就有22只脚；接着把鸡减少1只，兔增加1只，就有24只脚；最后再把鸡减少1只，兔增加1只，就有3只鸡5只兔，26只脚。

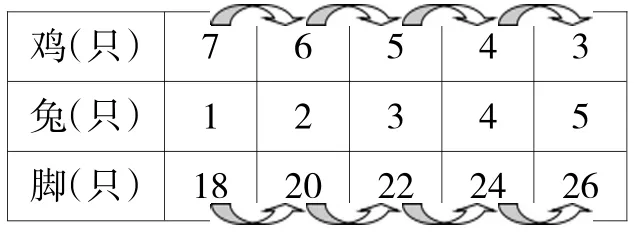
师：老师发现你调整的速度越来越快，是发现了什么吗？

生2：因为每把鸡减少1只，兔增加1只，总脚数就会增加2只。

师：这位同学是根据鸡兔只数的变化引起脚只数的变化规律，一步一步调整得到符合题意的答案。还有不一样的调整方法吗？

生3：我比他调整得快一些！

师：噢，说说看！

生3：我想，7只鸡1只兔，总脚数18只，比26只少，因此要增加兔的只数、减少鸡的只数。那么我就先试着调整到5只鸡3只兔，就有22只脚，还差4只脚；我就再增加2只兔，减少2只鸡，就有26只脚了。

师：我们听明白了，你是跨越式调整的。调整2次，就得到符合题意的答案。

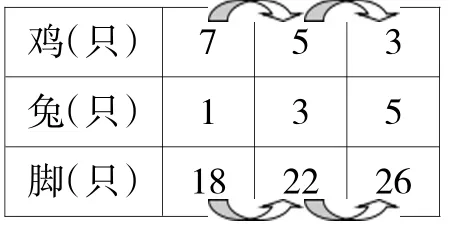
生4：老师，我们只用调整1次，就可以得到26只脚！

师：只调整1次？快来说一说！

生4：现在有18只脚，题目中有26只脚，相差8只，8÷2=4，就要减少4只鸡，增加4只兔，那么就是3只鸡5只兔。

师：8÷2中的“2”是什么意思？

生4:2就是每把1只鸡换成1只兔就会增加2只脚。

师：这位同学是在前两位同学调整的基础上根据规律，一步到位，调整成功。看来，无论是一步一步调整，还是跨越式调整，或是一步调整到位，都是抓住了鸡兔只数变化引起脚的只数变化的规律。我们利用这个规律，就能把猜测的结果通过调整得到符合题意的只数。刚才大家经历的这个猜测——调整的过程，就是假设的产生。

师：同学们，在刚才“猜测——调整”的过程中，无论你们是逐一调整，还是跳跃调整，甚至一步调整到位，都是抓住了鸡兔只数变化引起脚的只数变化的规律。你们发现这个规律了吗？谁能像他那样再说说这个规律？

生1：每把1只鸡换成1只兔就增加2只脚。

师：反过来呢？

生2：每把1只兔换成1只鸡就减少2只脚。

师：发现了这个规律，无论怎样假设，都能通过调整得到符合题意的只数。我们甚至还可以假设全部是鸡，也就是从8只鸡0只兔开始假设；或者假设全部是兔，也就是0只鸡8只兔开始假设。你们能用算式，把调整的过程表示出来吗?先想想，再试试看吧。

生1：假设全部是鸡。

2×8=16（只）

26-16=10（只）

10÷（4-2）=5（只）——兔

8-5=3在（只）——鸡

师：你是怎么想的？

生1：假设笼子里全是鸡，就有2× 8=16只脚，而笼子里实际有26只脚，这样就多出了26－16=10只脚，而1只兔比1只鸡多2只脚，这样就有10÷ 2=5只兔，鸡的数量就是8－5=3只了。

生2：假设全部是兔。

4×8=32（只）

32-16=6（只）

6÷（4-2）=3（只）——鸡

8-3=5（只）——兔

（配合课件演示）

师：像这样把极端假设的调整过程通过算式来体现，其实大家就体验了“假设”的运用。

师：我们刚才无论是极端假设还是随机假设，都是把鸡兔的只数假设成已知数，既然鸡、兔的只数我们可以假设成已知数，那么也可以把它们假设成？

生：未知数。

师：如果设兔的只数为x，那鸡的只数怎样用未知数表示？脚的总只数呢？

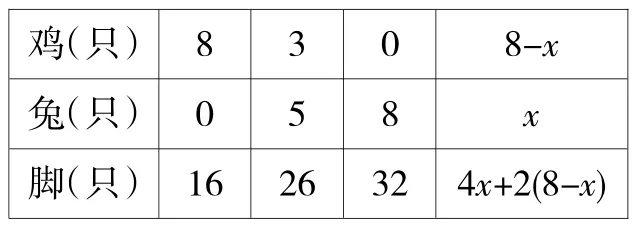
（随学生回答，用代数式表示）

师：4x+2(8-x)是什么意思？

生1：4x表示兔的脚数，2(8-x)表示鸡的脚数，4+2(8-x)表示鸡和兔的总脚数，在这里就是26只。这种假设你能用方程来解决吗？

（全班试做，指名演板，反馈交流）

生2：解：设兔有x只，则鸡有8-x只。

4x+2(8-x)=26

x=5

8－5=3（只）——鸡

答：鸡有3只，兔有5只。

师：像这样将未知数假设成字母x，用方程的方法解决问题，实际上也是“假设”思想的拓展应用。

【分析研究】

要想凸显数学的本质，达到数学广角的教学目的，我们需要对数学广角这类课型的特点进行分析。

数学广角的编排意义是：利用数学广角系统而有步骤地渗透数学思想方法，尝试把重要的数学思想方法通过学生可以理解的简单形式，采用生动有趣的、以学生容易接受的生活问题的形式呈现出来，使学生通过观察、操作、实验、猜测、推理与交流等活动，初步感受数学思想方法的奇妙与作用，受到数学思维的训练，逐步形成有序地、严密地思考问题的意识，同时使学生逐步提高探索数学问题的兴趣与欲望，不断强化发现、欣赏数学美的意识。

它的编排顺序是：

二年级上册、三年级上册“搭配问题”——主要渗透排列与组合思想；

三年级下册“兴趣小组的统计”——主要渗透集合思想；

四年级上册“烙饼、沏茶等合理安排”——主要渗透优化思想；

四年级下册“植树问题”——主要渗透建模、数形结合思想；

五年级上册“邮政编码”——主要渗透编码思想；

五年级下册“找次品”——主要渗透建模、化归思想；

六年级上册“鸡兔同笼”——主要渗透假设思想；

六年级下册“抽屉原理”——主要渗透建模思想。

那么，基于数学广角视野，我们再来重新审视“鸡兔同笼”问题的三种预设定位：是把它定位为专题讲座，或是介绍用多种方法解决这类问题，还是借“鸡兔同笼”的素材让学生经历“假设”思想的产生、应用及拓展过程？显然，我们会不约而同地选择后者。这，就是我们对这节课的定位。

那么，到底什么是假设思想呢？假设，是对题目中的已知条件或问题提出某些假设，然后按照题目中的已知条件进行推算，根据数量出现的矛盾，加以适当调整，最后找到正确答案的一种思想方法。它是一种有意义的想象思维，掌握之后可以使要解决的问题更形象、具体，从而丰富解题思路，发展学生的智力。

基于对这节课的定位和“假设思想”的解读，我们设计了这样的一条主线：

看似不经意的随意猜测，其实就是假设的雏形。学生在老师的带领下，运用“鸡、兔只数的变化引起总脚数的变化规律”对假设的结果进行调整，这样猜测——调整的过程让学生经历了假设的产生。在调整过程中，学生可以逐一调整，也可以跳跃调整，甚至一步到位，从中闪现了智慧的火花。列式计算则是极端假设的应用，假设全是鸡或假设全是兔其实就是极端假设。而方程就是假设的延伸拓展。如果我们将它假设成未知数，方程就应运而生了。由此看来，贯穿“猜测——调整——列式计算——方程解决”的主线就是对假设的定位与调整。

（作者单位：武汉市江岸区小学教研室）

责任编辑 王爱民