一种基于应变能理论的加速蠕变本构模型

沈才华,张 兵,王文武

(1．河海大学土木与交通学院,江苏南京 210098;2．中国矿业大学深部岩土力学与地下工程国家重点实验室,江苏徐州 221008)

一种基于应变能理论的加速蠕变本构模型

沈才华1,2,张 兵1,王文武1

(1．河海大学土木与交通学院,江苏南京 210098;2．中国矿业大学深部岩土力学与地下工程国家重点实验室,江苏徐州 221008)

采用连续介质应变能理论分析蠕变宏观力学行为突变的过程,定义临界应变能密度值作为预测加速蠕变发生时刻的控制参数,采用西原正夫元件模型与Perzyna黏塑性理论相结合,考虑应力状态对加速蠕变的影响,用过屈服应力比函数反映加速阶段蠕变应变速率变化,建立了一种能描述蠕变3个阶段全过程的加速蠕变本构模型。该方法确定的加速蠕变时刻不仅能反映累积蠕变应变量的影响,而且能有效反映应力状态对加速蠕变的影响,为实现预测加速蠕变提供了可能,并且确定本构模型参数所需试验数量大大减少,为实际运用提供了方便。最后结合三轴蠕变试验,采用D-P屈服准则结合塑性流动法则,分析了不同流动法则对预测加速蠕变发生时刻的影响规律,数值模拟结果与试验数据基本吻合。

应变能理论;蠕变本构模型;应变能密度;长期强度

岩石流变包括蠕变、应力松弛、长期强度等现象。其中,蠕变[1]特指恒定应力作用下应变随时间持续增长的现象,因其与工程实践联系紧密而成为流变研究领域中最重要的内容。其中加速蠕变阶段对工程稳定性起主要决定性作用,因此引起了学术界的重视,Vёiìalov考虑应力与应变速率之间的非线性关系,认为Bingham模型中黏滞元件的黏滞系数不是常数,而是变化的,并建立了修正Bingham定律[2];王军保、刘新荣等[3]基于非线性流变力学理论,提出了一种非线性黏滞体,其黏滞系数是所加应力水平和蠕变时间的函数,有效的模拟了等速蠕变状态;宋勇军等[4]借鉴经典元件模型的建模思路,将岩石的初始屈服强度作为蠕变硬化的应力阈值,岩石的长期强度作为损伤软化的应力阈值,引入能反映岩石硬化效应的硬化函数和损伤效应的损伤变量,建立能够全面反映蠕变机制的岩石非线性蠕变模型。

总的说来,目前岩石流变的理论研究,国外研究多集中于幂律本构或者内变量模型,而国内多数基于元件理论,即按照岩石的弹性、塑性和黏滞性设置基本元件(Hooke体、St．Venant体、Newton体)[5]建立由其串联或并联组合而成的模型,目前使用较多的有Kelvin模型、Burgers模型、西原模型、Sterpi和Gioda模型等[6-7]。其中,西原模型[1]因简单且能够比较清楚且全面地反映流变中的弹-黏弹-黏塑性而受到广大研究者的重视。

对于蠕变加速阶段如何判别和模拟研究还存在争议,目前大部分得到的都是经验性公式,理论研究不够,有的需要很多试验才能获得其本构公式,结果很难推广。Sih．G．C[8]采用应变能理论对裂纹扩展特性进行了研究,很好的解释了裂纹开展引起的宏观应力应变过程,成为分析含裂纹体应变场变化的有效方法,因此本文基于应变能理论,研究蠕变断裂过程,提出了基于Perzyna黏塑性理论结合西原模型的一种非线性蠕变统一本构模型。

1 基于应变能理论的加速蠕变模型

传统的西原模型由胡克体(H),黏弹性体(N/ H)和黏塑性体(N/St．V)组成,一维的西原本构方程可表示为

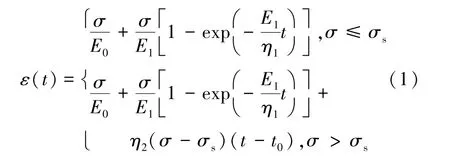
式中,E0为弹性模量;E1为黏弹性模量;η1和η2为黏滞系数;σ为总应力;ε为总应变;σs为长期强度; t0为初始屈服时刻。

西原模型中黏塑性阶段采用应变率为常数进行模拟,不能反映黏塑性加速蠕变,而Perzyna黏塑性理论[9-10]能很好地模拟材料的非线性黏塑性力学行为,其黏塑性应变率本构方程定义如下:

根据流变学理论,决定蠕变力学行为特征的主要因素应从材料内部考虑,根据应变能理论[11-13],材料的力学行为改变认为与其内能变化有关,可以采用应变能密度变化来描述。因此假设瞬时弹塑性应变与蠕变应变(总应变减去瞬时应变)产生的内部机理不同,即蠕变应变能密度变化控制了材料的蠕变行为的变化。结合岩石蠕变全过程特点,采用临界应变能密度值作为岩石蠕变过程中不同阶段的控制阀值,因此定义非零等速蠕变临界应变能密度值,其下限值为,当不同应力状态情况下,只要其应变能密度值超过其临界值,则岩石就将进入非零等速蠕变阶段。同理定义加速蠕变临界应变能密度值,其下限值为,当不同应力状态情况下,只要其应变能密度值超过其临界值,则岩石就将进入加速蠕变阶段(图 1)。因此式(3)中的φ(F)函数可用蠕变应变能密度函数[8,14-15]重新定义如下:

式中,F为屈服函数。

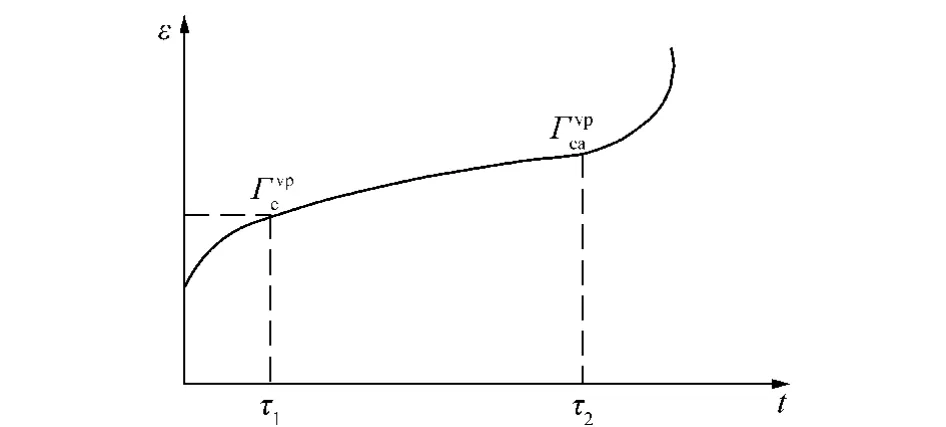
图1 蠕变临界应变能密度控制阀值示意Fig．1 Schematic diagram of control threshold creep strain energy density

由图1所示,岩石宏观蠕变应变变化过程一般分为3个阶段:第1段为衰减蠕变阶段,如果蠕变应变能密度值小于非零等速蠕变临界应变能密度值,岩石将不会进入等速蠕变阶段;第3阶段为岩石应变能密度值大于等于加速蠕变临界应变能密度值,岩石进入加速蠕变阶段;第2阶段处于两者之间为等速蠕变阶段。根据定义,非零等速蠕变临界蠕变应变能密度计算公式可以写为

其中,F∗(σ)为非零等速蠕变对应的应力状态函数;τ1为非零等速蠕变起始时刻。对于一维恒定荷载下的蠕变过程,式(5)可简写为

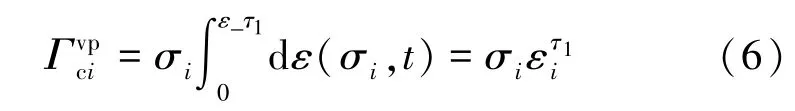
式中,σi为能进入非零等速蠕变的应力,即大于长期强度荷载时对应的应力;为非零等速蠕变起始时刻对应的蠕变应变值。

因此式(2)改写为

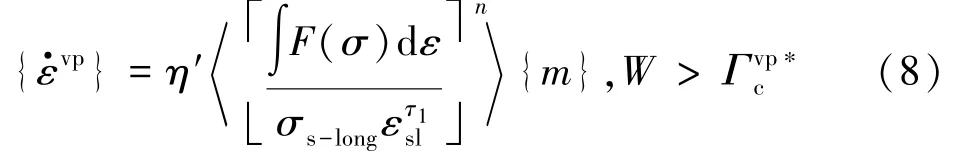
根据Perzyna黏塑性理论,{m}可取塑性流动方向,当采用相关联流动法则[16]时,可定义为与塑性流动方向一致,一维状态时等于1(为了容易理解,下面仍在公式中保留{m})。其中W为蠕变应变能密度值,一维情况下可简化为

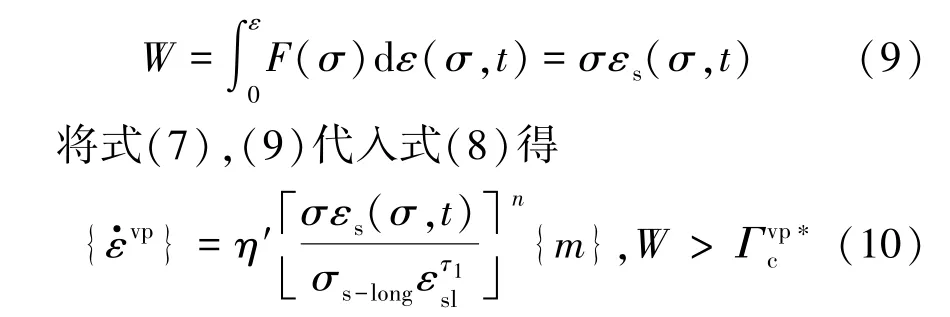
其中,εs(σ,t)为蠕变应变,在渐进破坏过程中是一个复杂函数,如果只在某一恒定加载条件下(σ为常数)进行蠕变过程研究,则εs(σ,t)可简化为时间的函数,可通过拟合试验结果获得εs(t)的表达式,假设采用多项式进行无限逼近蠕变过程曲线可得

如果k=0,则f(t)=a0,方程(12)简化为Perzyna黏塑性本构模型[5]。

因此将式(12)的黏塑性方程与西原模型结合可得改进的西原模型黏弹性、黏塑性阶段的本构方程如下:

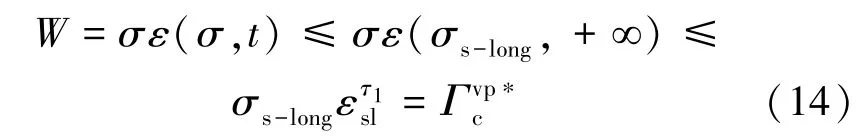
因此根据不等式递推理论,当k=0(即f(t)= a0),采用弹塑性理论中的流动法则[16]确定蠕变流动方向,则方程(13)退化为传统的西原模型。

等速蠕变与加速蠕变是岩石蠕变过程中截然不同的两种力学行为,根据前面加速蠕变临界应变能密度(图2)的定义,不同应力状态下应变能密度大于时,岩石进入加速蠕变阶段,此时式(11)中的f(t)明显是时间相关的函数,由于在同一种类型的应力状态下(如单轴受拉类型、单轴受压类型或三轴受压类型等)岩石进入加速蠕变时的破坏模式很相似,因此假设同一种岩石在两种不同应力状态下的加速蠕变临界应变能密度成函数关系,即属于同一种类型的任意进入加速蠕变的应力状态的临界应变能密度可表示成式(15)。

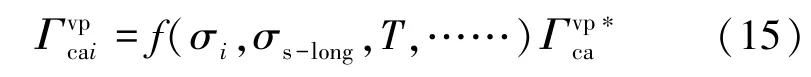
图2 蠕变过程临界应变能密度示意Fig．2 Schematic diagram of the strain energy density of accelerated creep

试验表明岩石在同一类型应力状态下(如三轴受压)的破坏模式基本是一致的,因此可以采用静力学连续介质应变能理论进行宏观应力应变分析[10]。应变能密度是标量值,如果把岩石视为连续均匀介质,则作为同一类型应力状态下的加速蠕变应变能密度的临界值(标量)不应受应力方向的改变而变化,因此可以视为常数,即式(16)中f(σi, σs-long)可近似取1。

因此可获得一维状态下基于应变能理论的能描述加速蠕变的统一黏弹塑性蠕变本构方程如下:

当n=1,k=1时,f(t)=a0+a1(t-τ2),蠕变统一本构方程式退化为Qinghui Jiang等[17]采用增加非线性黏滞壶的方式建立的加速蠕变本构模型。

根据实际情况,应力状态增加对加速蠕变的快慢也将起到影响,因此式(12)中k的取值(蠕变非线性特征参数,反映了蠕变加速的快慢)应该与过屈服应力比值大小有关[18],因此有式(20)成立。

因此结合一维本构方程推广到三维矩阵形式的类比法,得到基于应变能理论的可以描述加速蠕变过程的简化实用三维加速蠕变本构模型如下:

式中,带上划线的表示三维情况下对应的屈服强度计算值

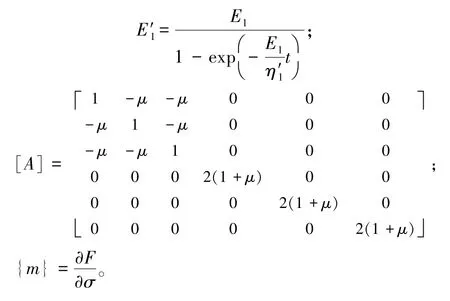
本构模型的参数可以通过岩石蠕变试验获得。假设采用 Drucker-Prager屈服准则,则

2 三轴蠕变试验的加速蠕变本构模型模拟分析

对某砂岩(图3)进行三轴蠕变试验,轴向压力61 MPa,围压6．0 MPa,采用最小二乘法,结合方程(21)～(23)进行拟合获得本构模型参数。采用D-P屈服准则和相关联流动法则建立三维本构模型(本构模型Ⅰ),根据实测曲线拟合的参数见表1,实测数据与本构模型Ⅰ的拟合曲线如图4所示。采用D-P屈服准则和非相关联流动法则(α=0)建立三维本构模型(本构模型Ⅱ)。实测加速蠕变发生时刻(τ2=36．2 h)的加速蠕变应变能密度值为0．169 J/m3。

图3 砂岩试样Fig．3 Sandstone specimens

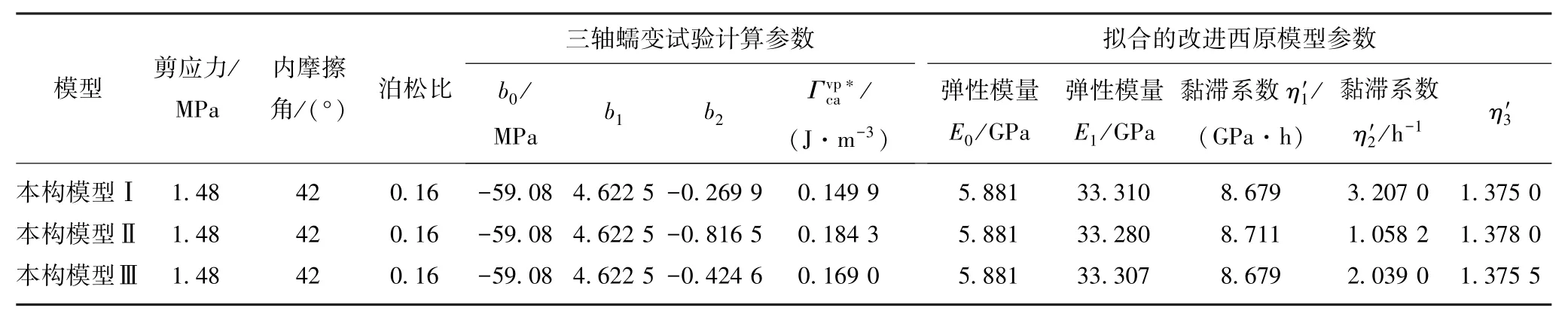
表1 本构模型计算参数Table 1 Parameters of the triaxial creep tests and the parameters of constitutive model

图4 实测值与本构模型Ⅰ拟合曲线Fig．4 The data of triaxial test and the fitting curve of modified Nishihara model

表1显示,采用不同的流动法则时对预测加速蠕变有较大影响。采用本构模型Ⅰ计算的实际加速蠕变起始时刻(τ2=36．2 h)对应的加速蠕变应变能密度值(0．149 9 J/m3)小于实测值(0．169 J/m3);采用本构模型Ⅱ计算的实际加速蠕变起始时刻(τ2= 36．2 h)对应的加速蠕变应变能密度值(0．184 3 J/m3)大于实际值(0．169 J/m3)。图5显示采用本构模型Ⅰ(α=0．331,相关联流动法则)预测的加速蠕变发生时刻比实际的晚,模拟结果偏于危险;采用本构模型Ⅱ(α=0)预测的加速蠕变发生时刻比实际的早,模拟结果偏于安全,可见非相关联流动法则的膨胀角对预测结果有很大影响,这与实际情况一致。因此取非相关联流动法则α=0．232时作为本岩样的本构模型(本构模型Ⅲ)。图5显示本构模型Ⅲ模拟计算曲线与实测值基本一致。

为了验证本构模型的合理性,采用本构模型Ⅲ对不同轴向应力作用下的蠕变全过程进行预测,结果如图6所示。

图5 不同本构模型模拟值与实测值对比曲线Fig．5 The data of triaxial creep test and the different constitutive model simulation curves

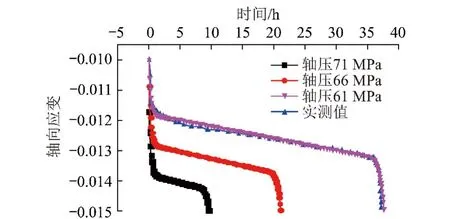
图6 轴向蠕变应变-时间曲线(本构模型Ⅲ,不同轴压)Fig．6 The time-strain curves of creep(constitutive modelⅢ and different axial pressures)

图6显示基于应变能理论建立的蠕变本构模型能有效描述蠕变三阶段全过程,预测不同轴向应力下的蠕变过程规律与实际情况基本相似。

3 结 论

(1)采用非线性黏塑性理论研究与元件方法相结合建立岩石蠕变的有限元本构模型,能很好地反映岩石蠕变全过程,为实现岩石蠕变过程数值模拟分析提供了一种途径。

(2)基于连续介质应变能理论,采用临界应变能密度值描述材料发生蠕变力学行为突变的特征量,该方法确定的加速蠕变时刻不仅能反映累积蠕变应变量的影响,而且能有效反映应力状态对加速蠕变的影响,为实现预测加速蠕变提供了可能,并且确定本构模型参数所需试验数量大大减少,为实际运用提供了方便。

(3)最后通过数值模拟与试验结果对比分析说明:采用本文方法获得的岩石蠕变本构方程能有效模拟衰减蠕变、等速蠕变和加速蠕变的全过程,采用非相关联流动法则的蠕变本构模型预测加速蠕变发生时刻比实测值早,相对偏于安全。本文提出的用蠕变临界应变能密度值预测加速蠕变发生时刻的方法为研究岩石蠕变破坏的宏观本构模型提供了新的思路。

[1] Nishihara M．Creep of shale and sandy-shale[J]．The Journal of Geological Magazine of Japan,1952,58:373-377．

[2] 齐亚静,姜清辉,王志俭,等．改进西原模型的三维蠕变本构方程及其参数辨识[J]．岩石力学与工程学报,2012,31(2):347-355．

Qi Yajing,Jiang Qinghui,Wang Zhijian,et al．3D creep constitutive equation of modified Nishihara model and its parameters identification[J]．Chinese Journal of Rock Mechanics and Engineering,2012, 31(2):347-355．

[3] 王军保,刘新荣,郭建强,等．盐岩蠕变特性及其非线性本构模型[J]．煤炭学报,2014,39(3):445-451．

Wang Junbao,Liu Xinrong,Guo Jianqiang,et al．Creep properties of salt rock and its nonlinear constitutive model[J]．Journal of China Coal Society,2014,39(3):445-451．

[4] 宋勇军,雷胜友,刘向科．基于硬化和损伤效应的岩石非线性蠕变模型[J]．煤炭学报,2012,37(S2):287-292．

Song Yongjun,LeiShengyou,Liu Xiangke．Non-linearrock creep model based on hardening and damage effect[J]．Journal of China Coal Society,2012,37(S2):287-292．

[5] De Borst R,Crisfield M A,Remmers J J C,et al．Time-dependent material models[A]．Non-Linear Finite Element Analysis of Solids and Structures,Second Edition[C]．2012:281-304．

[6] Tang M,Wang Z．Experimental study on rheological deformation and stress properties of limestone[J]．Journal of Central South University of Technology,2008,15(1):475-478．

[7] Sterpi D,Gioda G．Visco-plastic behaviour around advancing tunnels in squeezing rock[J]．Rock Mechanics and Rock Engineering, 2009,42(2):319-339．

[8] Sih G C．From monoscale to multiscale modeling of fatigue crack growth:Stress and energy density factor[J]．Science China Physics,Mechanics and Astronomy,2014,57(1):39-50．

[9] Zhou H W,Wang C P,Han B B,et al．A creep constitutive model for salt rock based on fractional derivatives[J]．International Journal of Rock Mechanics and Mining Sciences,2011,48(1):116-121．

[10] Zhou H W,Wang C P,Mishnaevsky Jr L,et al．A fractional derivative approach to full creep regions in salt rock[J]．Mechanics of Time-Dependent Materials,2013,17(3):413-425．

[11] Zhu Hehua,Ye Bin,Cai Yongchang,et al．An elasto-viscoplastic model for soft rock around tunnels considering overconsolidation and structure effects[J]．Computers and Geotechnics,2013,50:6-16．

[12] Xu W Y,Wang R B,Wang W,et al．Creep properties and permeability evolution in triaxial rheological tests of hard rock in dam foundation[J]．Journal of Central South University of Technology, 2012,19(1):252-261．

[13] Shibata K,Tani K,Okada T．Creep behavior of tuffaceous rock at high temperature observed in unconfined compression test [J]．Soils and Foundations,2007,47(1):1-10．

[14] Huang Y,Zhang Y,Zhang M,et al．Method for predicting the failure load of masonry wall panels based on generalized strain-energy density[J]．Journal of Engineering Mechanics,2014,140(8):1-12．

[15] Ayatollahi M R,Sedighiani K．Mode I fracture initiation in limestone by strain energy density criterion[J]．Theoretical and Applied Fracture Mechanics,2012,57(1):14-18．

[16] Lubliner J．Plasticity theory[M]．New York:Dover Publications, 2008．

[17] Jiang Qinghui,Qi Yajing,Wang Zhijian,et al．An extended Nishihara model for the description of three stages of sandstone creep [J]．Geophysical Journal International,2013,193(2):841-854．

[18] Rutter E H．On the creep testing of rocks at constant stress and constant force[J]．International Journal of Rock Mechanics and Mining Sciences&Geomechanics Abstracts,1972,9(2):191-195．

[19] 郑颖人,沈珠江,龚晓南．岩土塑性力学原理[M]．北京:中国建筑工业出版社,2002．

Zheng Yingren,Shen Zhujiang,Gong Xiaonan．The principles of geotechnical plastic mechanics[M]．Beijing:China Architecture& Building Press,2002．

A new accelerated creep constitutive model based on the strain energy theory

SHEN Cai-hua1,2,ZHANG Bing1,WANG Wen-wu1
(1.College of Civil and Transportation Engineering,Hohai University,Nanjing 210098,China;2.State Key Laboratory of Geomechanics and Deep Underground Engineering,China University of Mining and Technology,Xuzhou 221008,China)

The anthors analyzed the mutation process of the macro mechanical creep behavior from the perspective of the continuous strain energy theory,and defined the critical strain energy density to judge the occurrence time of accelerated creep．A accelerated creep constitutive model which can describe the whole process of transient creep,steady state creep,and accelerated creep was established by combining the Perzyna Visco-plasticity theory and Nishihara model,taking into account the influence of stress state on the accelerated creep and using the yield stress ratio to reflect the creep strain rate change of accelerated creep．The determined accelerating creep occurring time using this method not only reflectes the effect of cumulative strain of the creep,but also the influence of stress states on the accelerating creep,which provides possibility of prediction of the accelerating creep．In addition,the number of experiments to determine constitutive model parameters was significantly reduced,which is more convenient in practical applications．Finally,according to the triaxial creep test,the law that different flow rules affect the occurrence time of accelerated creep was analyzed by adopting Drucker-Prager yield criterion and plastic flow rule．As the simulation result is basically consistent with the test data,the research results provide a new method for the study of rock creep fracture process．

strain energy theory;creep constitutive model;strain energy density;long-term strength

TU452

A

0253-9993(2014)11-2195-06

2014-04-03 责任编辑:王婉洁

江苏省自然科学基金面上资助项目(BK20141419);深部岩土力学与地下工程国家重点实验室开放基金资助项目(SKLGDUEK1211);中央高校基本科研业务费专项资金资助项目(2014B04914)

沈才华(1976—),男,江苏宜兴人,讲师,博士。E-mail:shencaihua@163．com

沈才华,张 兵,王文武．一种基于应变能理论的加速蠕变本构模型[J]．煤炭学报,2014,39(11):2195-2200．

10．13225/j．cnki．jccs．2014．0445

Shen Caihua,Zhang Bing,Wang Wenwu．A new accelerated creep constitutive model based on the strain energy theory[J]．Journal of China Coal Society,2014,39(11):2195-2200．doi:10．13225/j．cnki．jccs．2014．0445