直墙半圆拱U型钢封闭支架控底力学模型及应用

唐芙蓉,刘 娜,郑西贵

(1．中国矿业大学理学院,江苏徐州 221116;2．中国矿业大学矿业工程学院,江苏徐州 221116)

直墙半圆拱U型钢封闭支架控底力学模型及应用

唐芙蓉1,刘 娜2,郑西贵2

(1．中国矿业大学理学院,江苏徐州 221116;2．中国矿业大学矿业工程学院,江苏徐州 221116)

针对深部巷道底臌治理难题,建立了直墙半圆拱整体支架的力学模型,运用极限载荷法推导了高应力条件下的支架承载能力和反拱临界失稳载荷,将反拱拱高与半径的比值定义为反拱控底影响因子ζ,研究了ζ在0～0．7范围内不同巷道宽度的反拱支架受力特征及稳定性。计算表明:对于净宽为5 m的巷道,反拱矢跨比宜取值在0．2～0．3,反拱控底影响因子和反拱半径的最佳取值分别为0．2和4 m,在淮南矿业集团丁集矿西11-2开拓巷道50 m试验段工程实践表明该支架对底臌具有良好的控制能力,2 a期的巷道底臌小于50 mm,且不需要卧底返修。

直墙半圆拱;U型钢封闭支架;反拱控底影响因子;深井巷道;底臌

目前我国东部矿区已经全面进入深部开采阶段,据不完全统计[1],全国已有 47对矿井埋深均超过1 000 m,对于这些深井巷道尤其是开拓巷道[2-3], 90%以上巷道断面形状为直墙半圆拱形,巷道宽度从4～6 m不等。淮南矿区中13对矿井开拓巷道年掘进量达200 km[4],巷道宽度多以5 m为主,这是目前深部大型矿井主流断面跨度,目前这类巷道通常所采用的支护方式为U型钢拱形可缩支架。U型钢拱形可缩金属支架于20世纪80年代引进中国并发展成9种架型,131种规格的支架,包括梯形、拱形和环形支架等[5-6]。然而在工程实践应用中存在颇多问题,如图1所示。

图1 U型钢拱形可缩支架破坏实照Fig．1 Supporting failure examples of U-shaped yieldable support

针对U型钢力学特性及控制机理,国内外学者进行了广泛研究,刘建庄等[7]对U型钢可缩支架的屈曲破坏特征进行了深入的研究,但没有对封闭支架整体受力特征及承载性能进行深入研究,蒋斌松等[8]对圆形可缩支架在较大荷载作用下或围岩产生较大变形情况下支架节产生缩动时,进行其内力的计算,该类封闭支架只局限于圆形巷道支护,高明中等[9]应用有限元软件ANSYS对马蹄形封闭支架进行数值模拟分析研究,并没有从理论上计算马蹄形支架受力的数值解;但直墙半圆拱巷道U型钢封闭支架的力学特性特别是其控底性能尚未深入研究,因此本文针对直墙半圆拱巷道U型钢封闭支架建立力学模型[10-11],分析其承载及控底性能,并利用强度校核法对支架进行材料选型,形成了一套完整的直墙半圆拱U型钢封闭支架设计思路。

1 封闭支架力学模型及受力分析

1.1 直墙半圆拱封闭支架力学模型

对模型做以下基本假设:① 由于永久性巷道不允许长时累计变形,在模型计算过程中,不考虑支架的可缩性;②模型着力分析巷道宽度为5 m时支架受力特征;③按照土力学中郎肯挡土墙理论,支架两侧受力实际是呈梯形分布的,考虑巷道高度和理论计算,本文将其简化为均布载荷,并考虑侧压系数λ;④将拱形支架与反拱连接处a,f两点简化为铰连接。

图2为直墙半圆拱U型钢封闭支架力学模型,拱顶和反拱的受力均为q,支架两侧的受力为λq,λ为侧压系数。拱顶为半圆形状,圆心在O1处,半径为R1,反拱为一段圆弧,圆心在O2处,半径为R2,拱的高度为h,直墙段高度为H。根据支架结构形状,把支架结构分为4段[12],即ab,be,ef和af。

对图2(a)中的支架结构模型进行分解为传统U型钢拱形支架图2(b)和反底拱部分图2(c),相对应的拱脚处的未知力分别为F1ah,F1fh,F1av,F1fv和F2ah, F2fh,F2av,F2fv。并利用材料力学中的叠加原理进行分段分析,最终叠加为支架的整体受力。

1.2 直墙半圆拱封闭支架力学性能分析

1.2.1 U型钢拱形支架受力计算

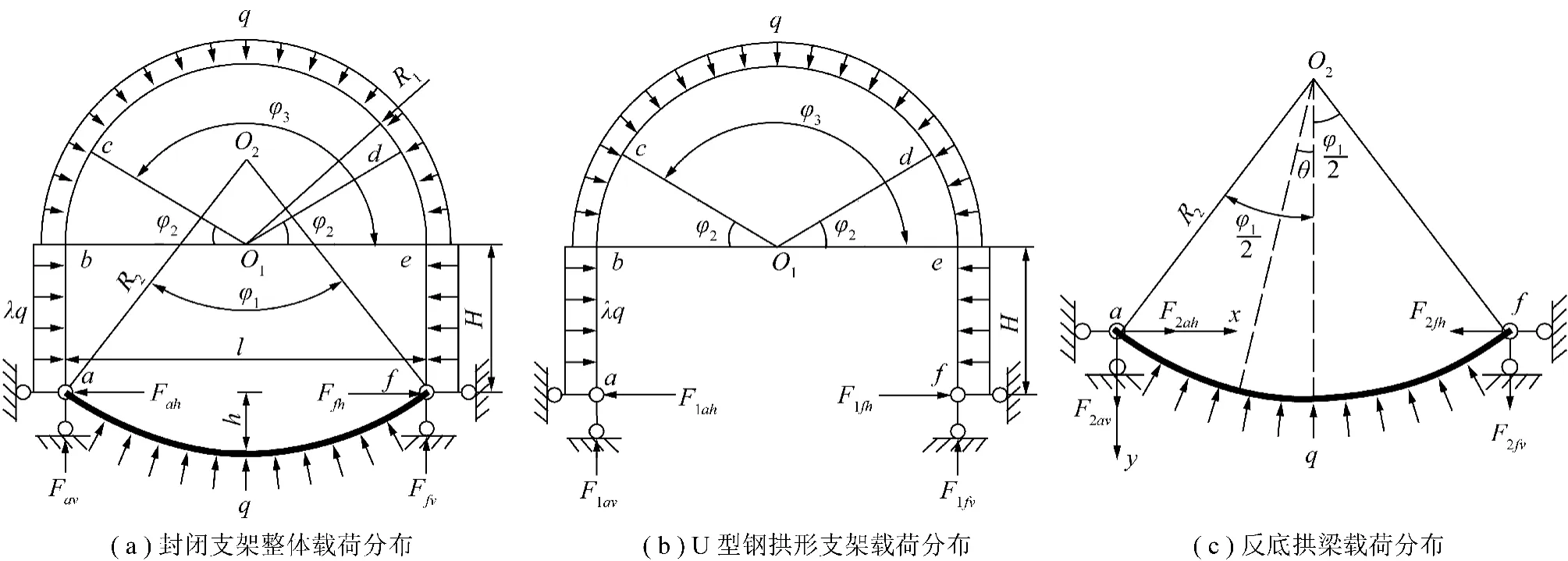
图2 直墙半圆拱封闭支架力学模型Fig．2 Mechanical model of closed support combined by straight wall and semicircular arch

首先计算图2(b)中af两点的垂直支反力,再计算图2(c)中反拱部分支反力,最后叠加即可。由于U型钢拱形支架受力在相关文献[5,13-14]已有详细的求解过程,这里只给出支架支反力简单的求解过程。图2(b)中柱腿铰支座af两点的垂直支反力,通过对半圆拱上均布载荷进行积分即得。

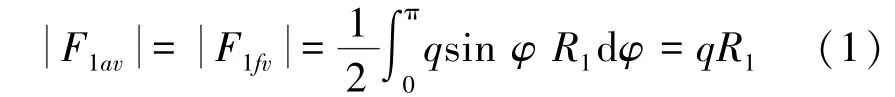
由于U型钢拱形支架中在铰支座处有4个未知量,所以为一次超静定结构,如图3所示,把未知力f解除结构变成静定结构,并用未知力X1代替f,应用材料力学中的力法准则方程:δ11X1+Δ1p=0(其中, X1为附加在f支座水平方向的多余约束力;δ11为当未知力X1=1单独作用在支架结构底支座f上,产生的水平位移,位移方向向右;Δ1p为支架在原有载荷q单独作用下,底支座f产生的水平位移,位移方向向左)。δ11和Δ1p都是位移的代数值,正负号表示位移的方向。

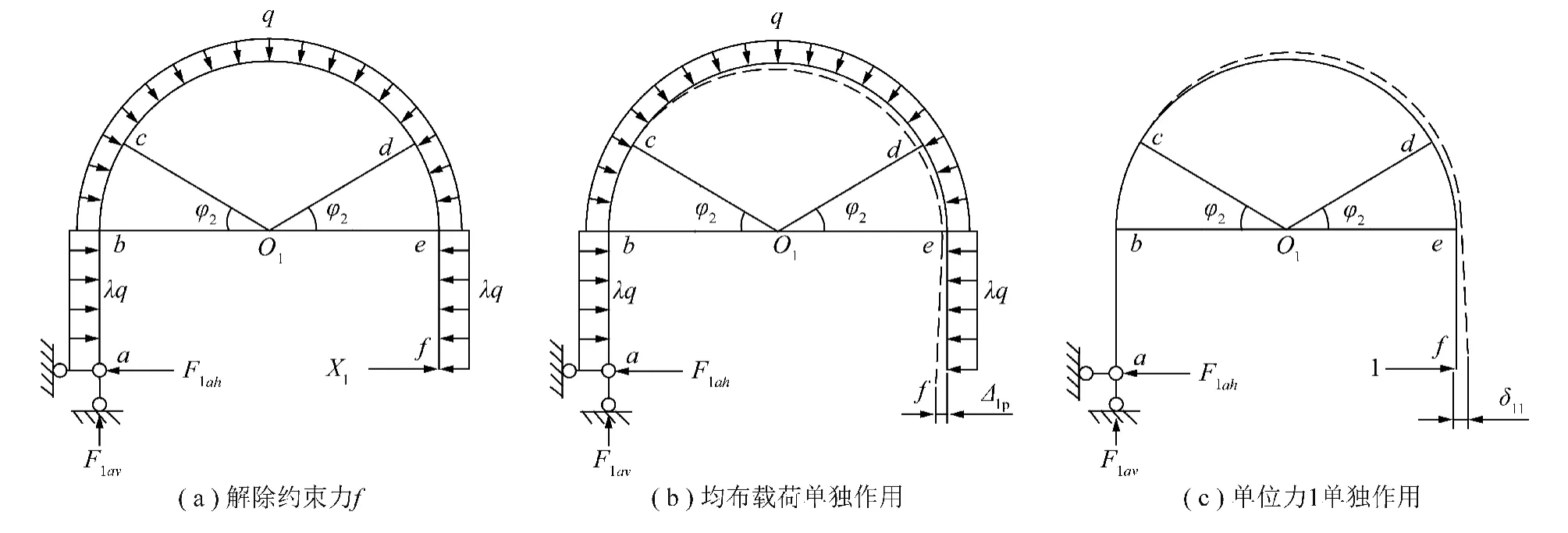
图3 基于力法方程U型钢拱形支架力学模型Fig．3 Mechanical models of the upper U-shaped support based on the Force-Method Equation

由图3可得,δ11和Δ1p的计算公式为

其中,Mp为支架原有载荷q在abef各段内分别产生的弯矩;为支架结构底支座f在未知力X1=1单独作用下各分段的弯矩;ds为支架结构轴向积分的微元长度;E为支架结构材料的弹性模量;I为支架结构各段对中性轴的惯性矩。由式(2),(3)得

1.2.2 封闭支架反拱受力计算

在图4中,反拱力学模型为两铰拱承受单一均布载荷[14],利用结构和荷载的对称性质,忽略轴向变形,只考虑弯曲变形[15];由于目前主流巷道宽度较大,反拱一般较平(h/l＜1/5),因此取ds=dx。由两铰拱相关的知识可知,拱轴线方程为

图4 反拱力学模型Fig．4 Analytical mechanical model of inverted arch

下面计算Δ1p,由于反拱受力对称,因此简支梁的弯矩Mx弯矩方程为

2 反拱梁极限载荷与控底影响因子分析

2.1 反拱失稳极限载荷

反拱极限载荷即指达到材料强度极限时的反拱破坏失稳载荷。对图2(c)中反拱取角度为θ的微元,建立反拱失稳后弯曲平衡微分方程,通过一系列求解得到反拱失稳后反拱的径向位移ω、环向位移μ以及反拱内任一微元截面弯矩M的表达式。根据煤矿现场对反拱破坏失稳形式调查认为反拱一般为正对称失稳,因此ω和M应为θ的偶函数,μ为θ的奇函数[16],所以可得

其中,θ为反拱中任一微元角度;n为正整数;ω为反拱失稳时的径向位移;μ为反拱两点的环向位移;M为反拱破坏失稳时,反拱内产生的弯矩。反拱边界条件为当θ=φ1/2时,ω=0,M=0及μ=0,由边界条件可建立齐次线性方程组[17]为

当给定φ1后,便可上式求解出n,进而求得反拱失稳时的极限载荷qcr。并由弹性稳定理论[18]得反拱纯压型极限载荷表达式为

其中,l为巷道宽度,m;K为反拱极限载荷系数,与矢跨比h/l有关。具体关系见表1。

表1 均布载荷反拱梁极限载荷系数Table 1 Ultimate load coefficient of inverted arch with equilibrium load distributed

该封闭支架其反拱与上部U型钢拱形支架连接处约束条件为两铰拱约束,由表1可知,反拱在承受均载情况下,矢跨比在0．3时,反拱的极限载荷系数最大,考虑到煤矿现场实际条件,要保留一定富裕系数,因此可以认为反拱矢跨比取0．2～0．3时,反拱极限载荷系数所对应的极限承载力对巷道支护效果经济合理。

2.2 反拱控底影响因子

本文分析的直墙半圆拱U型钢封闭支架主要考虑其对水平薄层状巷道底臌的控制,与传统的U型钢拱形支架不同的是在支架底部施加反底拱,形成直墙半圆拱U型钢封闭支架[19-20]。本节在以上分析基础上提出封闭支架反拱控底影响因子ζ,即ζ=h/R2,影响因子ζ范围不同,其控制底臌的稳定性也是不同的,由图2(c)得

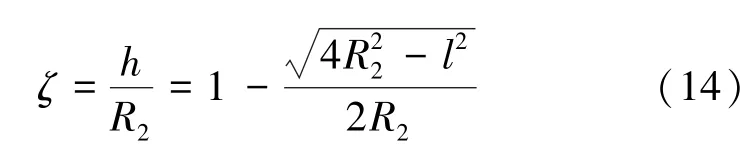
对式(14)利用Matlab数学软件进行拟合分析绘制影响因子的函数图像如图5所示。

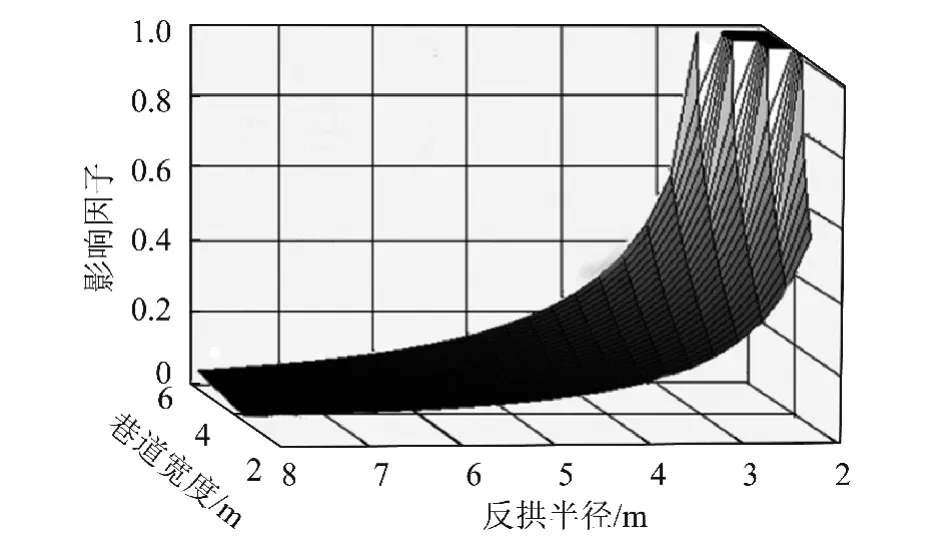
图5 影响因子曲面分布Fig．5 Curved surface distribution of influence factor(fitted by Matlab)

由函数图像可看出控底影响因子ξ在0～0．2图像为平缓稳定状态,在0．2～1．0图像为递增波动状态;当巷道宽度在3～6 m、反拱半径在2～8 m时,控底影响因子应根据上述的2种状态对反拱做出合理的实施措施,可认为当控底影响因子ξ在0～0．2,该支架对底板控制是合理可行的状态。

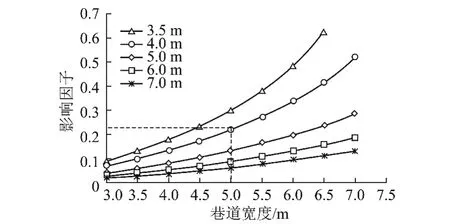
图6 不同反拱半径状态下巷道宽度与控底影响因子关系Fig．6 Relationship between the width of roadway and influence factor under different radius of inverted arch

由图6可得,控底影响因子取平缓稳定状态和递增波动状态的临界值0．2时,封闭支架控底稳定性为最佳;并应用Excel软件计算分析不同反拱半径状态下巷道宽度与控底影响因子之间曲线簇关系,可得到当巷道宽度为5 m、反拱半径为4 m时,控底影响因子近似为0．2,与应用Matlab拟合的基本一致。因此可以理论上得到当巷道宽度为5 m时,要想使反拱控底能够达到长时间稳定,反拱半径取4 m最佳。

3 封闭支架承载力解析计算和强度校核

封闭支架承载力分两部分:U型钢拱形支架加上底部反拱梁部分,两部分承载力相加便是直墙半圆拱U型钢封闭支架总承载力。在该结构中由于对称性只需要分3段,即ab,be和封闭支架反拱部分的af段。

3.1 U型钢拱形支架承载力

(1)U型钢拱形支架反拱部分ab段弯矩。

(2)U型钢拱形支架上部be段弯矩。

(3)反拱af段弯矩。

得到U型钢拱形支架的弯矩,利用强度校核准则对承载力进行计算。

其中,Mmax为支架结构中的最大弯矩;Wz为梁结构抗弯截面系数;[σ]为支架结构许用弯曲正应力,支架选用U36型钢。由式(15)可得到当U36型钢达到屈服强度时,支架承受的极限均布载荷qmax的值,利用qmax可计算出直墙半圆拱U型钢封闭支架上部的极限承载力。

3.2 封闭支架总承载力计算

因此支架总的承载力P为

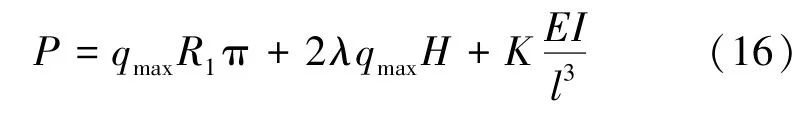
要确保直墙半圆拱U型钢封闭支架能够被动承载巷道周边给予的围岩压力,在支架进行设计和选型时,需根据地应力测试得到巷道周围的应力分布,利用式(16)计算所选支架的总承载力。

3.3 封闭支架强度校核

支架承载力虽然满足现场实际围岩压力条件,但是支架型钢材料的强度也必须经过验证计算,如此方可保证U型钢封闭选型的准确性合理性。上述为针对直墙半圆拱U型钢封闭支架的受力和强度进行理论上计算,下节将对该直墙半圆拱U型钢封闭支架在煤矿工程中应用效果进行数值分析研究。

4 算 例

4.1 工程概况

淮南丁集煤矿实际埋藏深度达930 m左右,设计生产能力为5．0 Mt/a,属于东部矿区典型的深井开采;西11-2四条开拓大巷是西11-2采区的咽喉要道,巷道布置在煤层底板岩层中,巷道断面尺寸为5．0 m×4．3 m,H=1 800 mm,在经受过上覆11-2煤层的采动影响后,巷道围岩变形、破坏,尤其是巷道底臌十分严重,导致其整体呈现出结构失衡,严重威胁到矿井安全高效生产。

选用直墙半圆拱U型钢封闭支架相关参数为φ1=1．3 rad(即72°),R1=2 500 mm,φ2=0．63 rad(即35°),R2=4 000 mm,由于巷道受力较大,支架选用Q390材质制成,Q390指屈服强度为390 MPa[12], U36型钢支架的抗弯截面系数Wx=137×10-6m3,通过在现场观测过程中得到支架拱顶的载荷集度为q= 190×103N/m,由于该矿属深井开采,并根据在此巷道的地应力测试结果选取侧压系数为λ=1．1,所以支架帮部的水平载荷集度 λq=209×103N/m。由式(4)可以计算得知直墙半圆拱U型钢封闭支架上部的直墙半圆拱部分水平支反力F1ah=F1fh=145 kN,由式(8)可得到封闭支架反底拱的水平支座反力为F2ah=F2fh=275 kN。

4.2 承载力计算

当已知支架结构和断面尺寸、型钢材料以及支架上的载荷分布时,应计算出该直墙半圆拱U型钢封闭支架能给巷道周边围岩提供的承载力,支架承载力根据式(16)计算得P=3．198 46 MN,由于设计棚距为0．5 m,支架承载力换算为对围岩的支护强度σ= P/Sk,其中Sk为封闭支架对底板控底面积。因此支架总的支护强度 σ=3．198 46/6．8=0．47 MPa＞0．4 MPa。

由条件可知该矿选用支架反拱半径R2= 4 000 mm,巷道宽度l=5 000 mm,由式(14)可得控底影响因子ζ近似为0．2,和理论推导基本一致,因此该支架控底稳定性处于稳定状态。且该支架支护强度能够达到0．4 MPa,满足对深部巷道底臌的控制要求。

4.3 强度校核

由以上的支架设计参数并且根据3．3节推导的强度校核公式对该封闭支架进行强度校核。

4.4 工程控制效果

针对淮南丁集煤矿西11-2轨道大巷,在无开采影响的一段静压巷道内,选取50 m作为试验地段,支护参数和强度按照前文推导可得,工程试验表明对巷道底板起到了很好的控制作用,2 a期的巷道底臌小于50 mm,可以认为此类U型钢封闭支架对深部静压巷道底板控制起到了很好的控制作用,控制效果如图7所示。

图7 实施U型钢封闭支架2 a后的底板支护效果Fig．7 The implementation of U-shaped closed supporting effect of anchor beam after 2 years

5 结 论

(1)建立直墙半圆拱U型钢封闭支架力学模型,应用结构力学方法把封闭支架简化为钢结构力学模型,解出支架在拱角连接处的支反力,运用极限载荷法对反拱的失稳极限载荷进行计算,并利用强度校核法检验其稳定性,提出反拱失稳极限载荷系数为0．3时,其承载能力达到最大。

(2)提出在水平薄层状巷道围岩条件下反拱控底影响因子ζ,并通过Matlab数学软件对取值范围进行三维图像绘制,可以看出当0＜ζ＜0．2时,巷道底板围岩控制效果为经济合理且稳定的状态,当0．2＜ζ＜1为递增波动状态,控制效果不稳定。在Matlab拟合基础上,得出反拱控底影响因子取临界值0．2时为最佳,并应用Excel软件计算分析不同反拱半径状态下巷道宽度与控底影响因子之间曲线簇关系,得到巷道宽度为5 m时,反拱半径取4 m为最佳支护状态。

(3)利用本文提出的力学模型指导淮南矿区丁集煤矿西11-2开拓大巷中直墙半圆拱U型钢封闭支架支护设计,通过连续矿压观测得到2 a期的巷道底板变形始终控制在50 mm以下,证明本文提出的力学模型及设计思路对直墙半圆拱U型钢封闭支架支护技术设计有较有益参考价值。

[1] 张 农,李希勇,郑西贵,等．深部煤炭资源开采现状与技术挑战[A]．全国煤矿千米深井开采技术座谈会[C]．泰安,2013．

Zhang Nong,Li Xiyong,Zheng Xigui,et al．Present status and challenges of deep mining of coal resources[A]．Mining Technology of National Thousand-Meter-Deep Coal Mines[C]．Taian,2013．

[2] 王卫军,冯 涛．加固两帮控制深井巷道底臌的机理研究[J]．岩石力学与工程学报,2005,24(5):808-811．

Wang Weijun,Feng Tao．Study on mechanism of reinforcing sides to control floor heave of extraction opening[J]．Chinese Journal of Rock Mechanics and Engineering,2005,24(5):808-811．

[3] 谢和平,彭苏萍,何满潮,等．深部开采基础理论与工程实践[M]．北京:科学出版社,2006．

Xie Heping,Peng Suping,He Manchao,et al．Deep mining basic theory and engineering practice[M]．Beijing:Science Press,2006．

[4] 袁 亮．深井巷道围岩控制理论及淮南矿区工程实践[M]．北京:煤炭工业出版社,2006．

Yuan Liang．Control of surrounding strata in deep mine roadway and practice in huainan area[M]．Beijing:China Coal Industry Publishing House,2006．

[5] 侯朝炯．巷道金属支架[M]．北京:煤炭工业出版社,1989．

Hou Chaojiong．Roadway steel support[M]．Beijing:China Coal Industry Publishing House,1989．

[6] 郑西贵,刘 娜,张 农,等．深井巷道挠曲褶皱性底臌机理与控制技术[J]．煤炭学报,2014,39(3):417-423．

Zheng Xigui,Liu Na,Zhang Nong,et al．Floor heave mechanism and control technology of flexural&folded deep mine roadway[J]．JournaL of China Coal Society,2014,39(3):417-423．

[7] 刘建庄,张 农,郑西贵,等．U型钢支架偏纵向受力及屈曲破坏分析[J]．煤炭学报,2011,36(10):1647-1652．

Liu Jianzhuang,Zhang Nong,Zheng Xigui,et al．Research on buckling failure mechanism of U type steel support loaded deviating longitudinally[J]．Journal of China Coal Society,2011,36(10):1647-1652．

[8] 蒋斌松,冯 强,王 涛,等．封闭式可缩性金属支架解析计算[J]．岩土力学,2011,32(6):1620-1624．

Jiang Binsong,Feng Qiang,Wang Tao,et al．Mechanical analysis of close type yieldable steel support[J]．Rock and Soil Mechanics, 2011,32(6):1620-1624．

[9] 高明中,李 伟．封闭式金属支架架型优选及应用[J]．煤炭科学技术,2007,35(2):16-19．

Gao Mingzhong,Li Wei．Type optimized selection and application of closed metal supports[J]．Coal Science and Technology,2007, 35(2):16-19．

[10]

Chen Yong,Bai Jianbiao,Yan Shuai,et al．Control mechanism and technique of floor heave with reinforcing solid coal side and floor corner in gob-side coal entry retaining[J]．International Journal of Mining Science and Technology,2012,22(6):841-845．

[11] 李学彬,杨仁树,高延法,等．大断面软岩斜井高强度钢管混凝土支架支护技术[J]．煤炭学报,2013,38(10):1742-1748．

Li Xuebin,Yang Renshu,Gao Yanfa,et al．High-strength steel tubular confined concrete supports support technology for large section soft rock inclined shaft[J]．Journal of China Coal Society, 2013,38(10):1742-1748．

[12] 魏建军,蒋斌松．钢管混凝土可缩拱架承载性能试验研究[J]．采矿与安全工程学报,2013,30(6):805-811．

Wei Jianjun,Jiang Binsong．Experimental study on structural property of contractible concrete-filled steel tube support[J]．Journal of Mining&Safety Engineering,2013,30(6):805-811．

[13] 龙驭球,包世华．结构力学教程[M]．北京:高等教育出版社, 2001．

Long Yuqiu,Bao Shihua．The course of structural mechanics[M]．Beijing:Higher Education Press,2001．

[14] 荆升国．高应力破碎软岩巷道棚-索协同支护围岩控制机理研究[D]．徐州:中国矿业大学,2009．

Jing Shengguo．Study on control mechanism of cooperating support of frame and anchor cable in soft fragmentized surrounding rock roadway with high stress[D]．Xuzhou:China University of Mining and Technology,2009．

[15] 张 农,李宝玉,李桂臣,等．薄层状煤岩体中巷道的不均匀破坏及封闭支护[J]．采矿与安全工程学报,2013,30(1):1-6．

Zhang Nong,Li Baoyu,Li Guichen,et al．Inhomogeneous damage and sealing support of roadways through thin bedded coal-rock crossovers[J]．Journal of Mining&Safety Engineering,2013, 30(1):1-6．

[16] 李廉辊．结构力学[M]．北京:高等教育出版社,2010．

Li Liangun．Structural mechanics[M]．Beijing:Higher Education Press,2010．

[17] 刘建庄．U型钢支架屈曲机理及控制[D]．徐州:中国矿业大学,2013．

Liu Jianzhuang．Controlling mechanism of U-steel frame buckling [D]．Xuzhou:China University of Mining and Technology,2013．

[18] 铁摩辛柯S P,盖莱J M．弹性稳定理论(第二版)[M]．北京:科学出版社,1958．

[19] 刘 刚,龙景奎,刘学强,等．巷道稳定的协同学原理及应用技术[J]．煤炭学报,2012,37(12):1975-1981．

Liu Gang,Long Jingkui,Liu Xueqiang,et al．Synergetic principle for roadway stability and its application technique[J]．Journal of China Coal Society,2012,37(12):1975-1981．

[20] 刘泉声,刘学伟,黄 兴,等．深井软岩破碎巷道底臌原因及处置技术研究[J]．煤炭学报,2013,38(4):566-571．

Liu Quansheng,Liu Xuewei,Huang Xing,et al．Research on the floor heave reasons and supporting measures of deep soft-fractured rock roadway[J]．Journal of China Coal Society,2013,38(4): 566-571．

Anti-floor heaven mechanical model and application of closed U-shaped support formed by straight wall and semicircular arch

TANG Fu-rong1,LIU Na2,ZHENG Xi-gui2
(1.College of Sciences,China University of Mining&Technology,Xuzhou 221116,China;2.School of Mines,China University of Mining&Technology, Xuzhou 221116,China)

In order to solve the problems of floor heave in deep collieries,an integral mechanical model,which was the combination of semicircular arch and straight wall,was proposed．Then the bearing capacity and critical buckling load of the proposed model under high stress state was successfully deducted using ultimate load method．Thus an influence factor ζ,ratio of radius and height of inverted arch was defined,and thereafter,the mechanical characteristic and stability of this kind of anti-floor heave model under different entry’s widths were also specifically investigated as ζ varied from 0-0．7．The results show that as to an entry with net width 5 m,the appropriate value for the rise span ratio of inverted arch is any of the value between 0．2 and 0．3 while the optimum value of ζ and radius are 0．2 and 4 m,respectively．Aforementioned mechanical model guided faultlessly in Western 11-2 Development Roadway at Dingji Mine, Huainan Mining Group,and the two-year-long floor heave convergence is less than 50 mm,which testify that this newfashioned prop shows a prefect floor heave control capability．

straight wall combined with semicircular arch;U-shaped closed prop;influence factor of inverted arch; deep roadway;floor heave

TD353

A

0253-9993(2014)11-2165-07

2014-03-28 责任编辑:常 琛

国家自然科学基金资助项目(51204519);中央高校基本科研业务经费专项资金资助项目(2011QNB05)

唐芙蓉(1972—),女,江苏响水人,讲师,博士。E-mail:menglidigushi3347@sina．com

唐芙蓉,刘 娜,郑西贵．直墙半圆拱U型钢封闭支架控底力学模型及应用[J]．煤炭学报,2014,39(11):2165-2171．

10．13225/j．cnki．jccs．2014．0409

Tang Furong,Liu Na,Zheng Xigui．Anti-floor heaven mechanical model and application of closed U-shaped support formed by straight wall and semicircular arch[J]．Journal of China Coal Society,2014,39(11):2165-2171．doi:10．13225/j．cnki．jccs．2014．0409