盾构机土压平衡系统的ARMA模型及其参数估计

李守巨,霍军周,曹丽娟

(1．大连理工大学工业装备结构分析国家重点实验室,辽宁大连 116023;2．大连理工大学机械工程学院,辽宁大连 116023;3．大连海洋大学机械与动力工程学院,辽宁大连 116023)

盾构机土压平衡系统的ARMA模型及其参数估计

李守巨1,霍军周2,曹丽娟3

(1．大连理工大学工业装备结构分析国家重点实验室,辽宁大连 116023;2．大连理工大学机械工程学院,辽宁大连 116023;3．大连海洋大学机械与动力工程学院,辽宁大连 116023)

为了表征盾构机土仓压力平衡系统的时滞特性和提高模型的预测精度,建立了该系统的自回归滑动平均(ARMA)模型,并提出了基于优化算法的ARMA模型参数估计方法。实验结果表明,与经典的线性机理模型相对比,新模型显著提高了土仓压力的拟合和预测精度。ARMA模型预测土仓压力的最大相对误差从机理模型的41%降低到9%。结合实验数据,分析了该系统动态响应的时滞特性,分析表明,螺旋输送机转速对下一时刻土仓压力影响的时滞特性更加明显。

自回归滑动平均模型;参数估计;土压平衡系统;盾构机;时滞特性

土压平衡盾构机是地铁隧道掘进过程中经常使用的机器类型之一,其土仓压力的大小直接影响到掘进工作面的土压力,决定了地表变形特征。因此,对盾构机土仓压力平衡动态系统模型的研究引起了国内外的普遍关注。刘宣宇等提出了一种基于土仓压力场梯度的土压平衡盾构开挖面稳定性的判定方法,利用非均匀B样条最小二乘方法建立了密封舱压力场的分布模型[1];笔者基于改性后渣土的非线性本构关系,建立了盾构机土仓平衡系统的动态模型,提出了基于遗传算法的土仓压力系统模型参数辨识方法[2];Xu等在实验室和现场研究了土压平衡盾构机土仓压力控制问题[3];Yang等建立了基于PID的土仓压力控制模型,提出了盾构机推进系统的比例控制方法,并且在实验台验证了控制算法的有效性[4];施虎等归纳了盾构设计和制造中所涉及到的6项关键技术,介绍盾构掘进模拟试验方法及模拟试验中的相似关系,重点论述体现盾构模拟试验技术先进性的模拟试验平台的研制进展和现状[5];王洪新采用流体力学理论推导了近似的土仓压力及刀盘开口处压力差计算方法,通过现场监测数据和离散元分析结果对公式进行了验证和修正[6];施虎等采用自适应神经模糊推理系统(ANFIS)建立了一个以推进力、推进速度、土仓压力实时数据采样值为输入,螺旋输送机转速为输出的基于排土控制的盾构土压平衡控制模型[7];夏毅敏等针对某地铁施工工程需求,应用所开发的复合式土压平衡盾构刀盘CAD系统进行了刀盘优化设计[8]。由于盾构机所穿越地层本身的复杂性和随机性、土仓内渣土本构关系的非线性、土仓压力变化对螺旋输送机转速改变响应的延迟性和渣土改性的不确定性,使得盾构机土仓压力平衡系统具有时变性、时滞性、不确定性和非线性特性,很难从物理和力学、数学本质上得到精确的解析机理模型。尽管如此,机理模型却能够表征系统在线性、确定性和趋势性上的输入与输出之间的内在映射关系。为了解决机理模型预测精度低、无法表征系统非线性和时变性问题,某些基于观测数据的统计模型建模方法逐步为学术界所重视,其中有代表性的是自回归滑动平均(ARMA)模型的统计建模方法。ARMA模型已经广泛应用到模型辨识[9]、风速预测[10-11]、能力需求预测[12]、过程报警预测[13]、最优估计[14]、不确定性系统建模等领域[15],并且显示了其优越性。但是,如何将ARMA建模方法应用到盾构机土压平衡系统建模鲜见报道。本文基于盾构机土仓压力平衡系统的线性机理模型,提出一种新的盾构机土压平衡系统自回归滑动平均模型,表征盾构机土仓压力平衡系统的时滞特性,并实验验证新模型的有效性。

1 盾构机土压平衡系统的自回归滑动平均模型

盾构机土仓压力受盾构机推进速度和螺旋输送机的转速影响,在大多数情况下,盾构机的推进速度设定为常数,通过实时调整螺旋输送机的转数控制土仓的压力,进而控制掘进工作面的土压力,最终实现控制地表变形的目的。当盾构机的推进速度为固定值时,盾构机土仓压力与螺旋输送机转速之间的线性机理模型[2]为

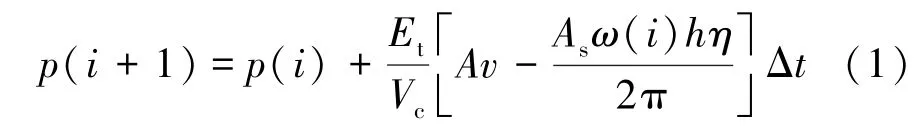
其中,p(i)和p(i+1)分别为当前时刻和下一时刻土仓压力;Δt为采样间隔时间;v为盾构机的推进速度; A为盾构机的横截面积;h为螺旋输送机的螺距;η为螺旋输送机的排土效率;ω(i)为当前时刻的螺旋输送机转速;As为螺旋输送机的有效排土面积;Vc为盾构机土仓体积;Et为渣土的等效变形模量。式(1)所建立的动态系统模型所存在的缺点在于没有考虑到该系统的时滞特性,导致模型预测精度较低。

受式(1)的启发,根据图1所建立的盾构机土压平衡系统的输入与输出关系,考虑到该系统的时滞特性,提出如下盾构机土仓压力平衡系统的自回归滑动平均(ARMA)模型:

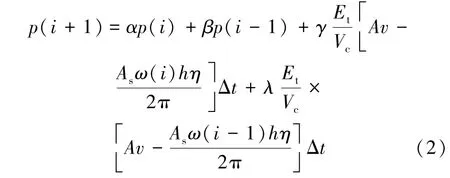
其中,α,β,γ和λ为待估计模型中的系数;p(i-1)和ω(i-1)分别为前一时刻的土仓压力和螺旋输送机转速。ARMA模型中的第1,2项为系统输出(盾构机土仓压力)的过去值的组合,即自回归部分,反映土仓压力过去值对当前值的影响;第3,4项为系统输入(即螺旋输送机的转数)过去值的组合,即滑动平均部分,反映螺旋输送机转数过去值对土仓压力当前值的影响。在盾构机土仓压力平衡系统的ARMA模型参数确定之后,该模型就可以预测盾构机土仓压力随螺旋输送机的变化规律,为盾构机土仓压力控制提供系统模型。

图1 盾构机土压平衡系统的输入与输出Fig．1 Input and output of earth pressure balance system of shield

2 盾构机土压平衡系统ARMA模型参数估计

在盾构机土仓压力平衡系统的ARMA模型中,除了需要辨识确定的渣土的等效切线变形模量(Et)和螺旋输送机的排土效率(η)之外,还包括系数α, β,γ和λ,而模型中的其他参数都是确定量。为了估计系统模型中的参数,定义如下的均方根误差(root mean square error)为目标函数:

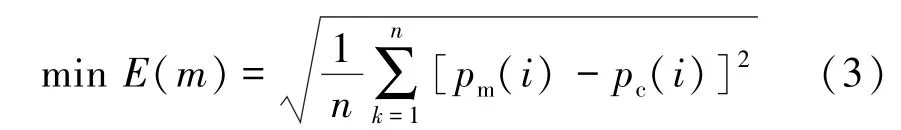
其中,pc(i)为按照式(2)由系统ARMA模型计算得到的土仓压力,它是未知的模型参数矢量m={Et,η, α,β,γ,λ}T的函数,被辨识的模型参数包括渣土的等效变形模量Et和螺旋输送机的排土率η以及系数α,β,γ和λ;pm(i)为实验观测到的土仓压力;n为采样数量。式(3)将系统辨识问题转化为无约束优化问题,可以采用非线性最小二乘法、遗传算法等优化方法求解。土压平衡系统ARMA模型参数估计就是根据实验观测数据,在模型结构已知的条件下,采用基于优化搜索的系统辨识方法,通过不断修正ARMA模型中的参数,使得ARMA模型的输出(pc)与实验观测的土仓压力(pm)之间的误差达到最小值,如图2所示。

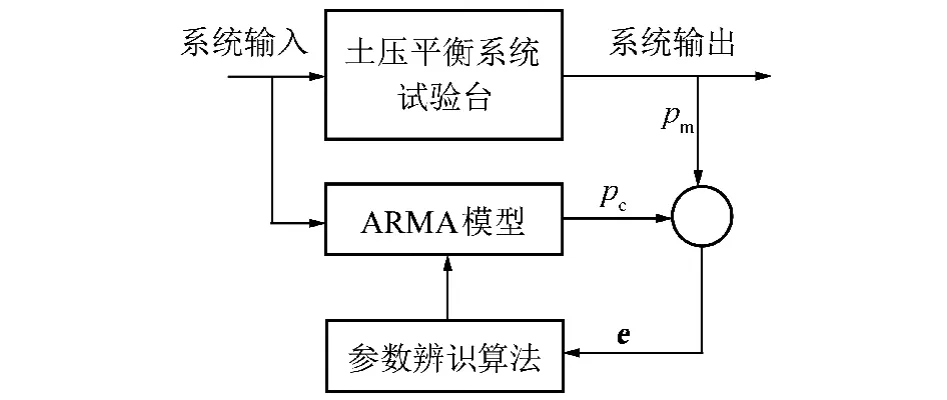
图2 ARMA模型参数估计Fig．2 Parameter estimation of ARMA model

为了获得目标函数的极小值,估计ARMA模型中的参数,采用Gauss-Newton方法对参数估计问题进行求解。与拟牛顿算法相对比,Gauss-Newton方法不需要计算海森(Hessian)矩阵,而且收敛速度高于其他梯度搜索算法,其迭代格式为

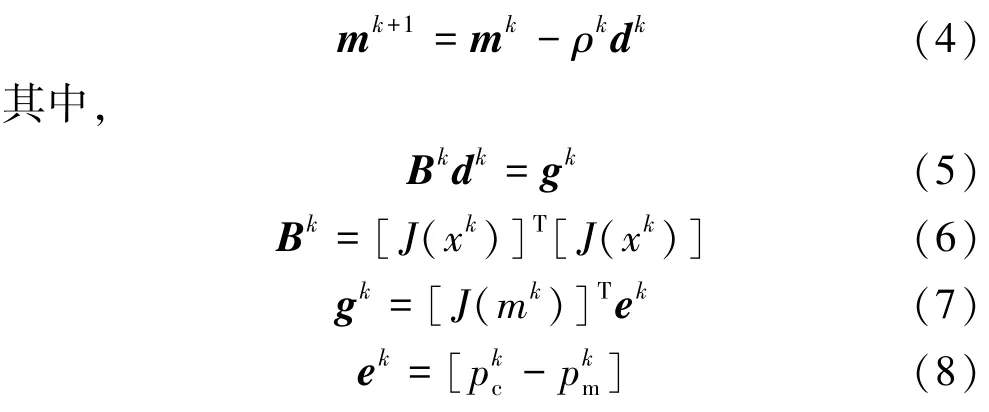
其中,e为误差矢量;J为ARMA模型计算的土仓压力对模型参数的Jacobian矩阵;ρk为迭代步长;dk为Gauss-Newton方向矢量;k为迭代次数,而步长ρk可以通过二次插值方法或者试错方法优化确定。Jacobian矩阵J中的元素由灵敏度系数表示

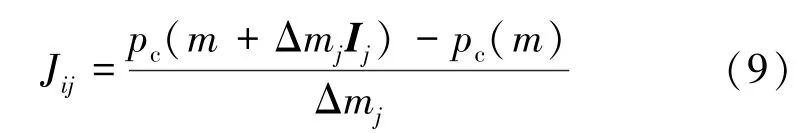
其中,Jij为第i时刻土仓压力计算值对第j个模型参数mj的灵敏度;Δmj为第j个模型参数增量;Ij为第j个单位矢量。当不同时刻土仓压力观测值和螺旋输送机的转速已知,根据目标函数(3),采用Gauss-Newton优化搜索方法就可以估计出ARMA模型中的参数。

3 实验研究

为了验证所提出新模型的有效性,在大连理工大学盾构机试验台上进行了实验研究。盾构机土仓压力控制试验台由液压油缸推进系统、刀盘旋转驱动系统、螺旋输送机排土系统、观测数据采集系统和土仓压力控制系统组成(图3)。其中,推进系统的推进速度是参考盾构机实际掘进速度和试验台模型的比例确定的,并且由PLC程序控制。根据螺旋输送机和盾构机试验台推进装置的基本特性,确定采样间隔时间为1 s,土仓压力的初始压力为56 kPa,刀盘的推进速度为v=20 mm/min,设计的螺旋输送机转速在0．2～1．2 rad/s变化,如图4所示;观测的土仓压力在10～80 kPa变化,如图5所示。螺旋输送机的主要几何特征尺寸为有效面积As为18 142．7 mm2,螺距h为128 mm,排土速率q为36．8×10-6mm3/s,平衡转速为0．573 rad/s,推进速度为20 mm/min,螺旋输送机排土率η=1．0。土仓的主要几何特征尺寸直径为 900 mm,宽度为 128 mm,横截面积 A为0．636 m2,体积Vc为0．081 4 m3。土仓内渣土的改性材料包括膨润土泥浆、泡沫和水,3种改性材料占原状土体的比例分别为6%,20%和10%左右。

图3 盾构机土仓压力控制试验台Fig．3 Testing device for controlling earth pressure in chamber of shield

根据图4螺旋输送机转速随时间变化和图5土仓压力随时间变化的实验数据,以及新建的土仓压力系统的ARMA模型,采用优化方法估计ARMA模型中的参数,表1给出了根据实验数据得到的线性机理模型和ARMA模型的参数。在图3,4中,前240组数据用来进行模型参数估计,后120组参数用来进行预测。

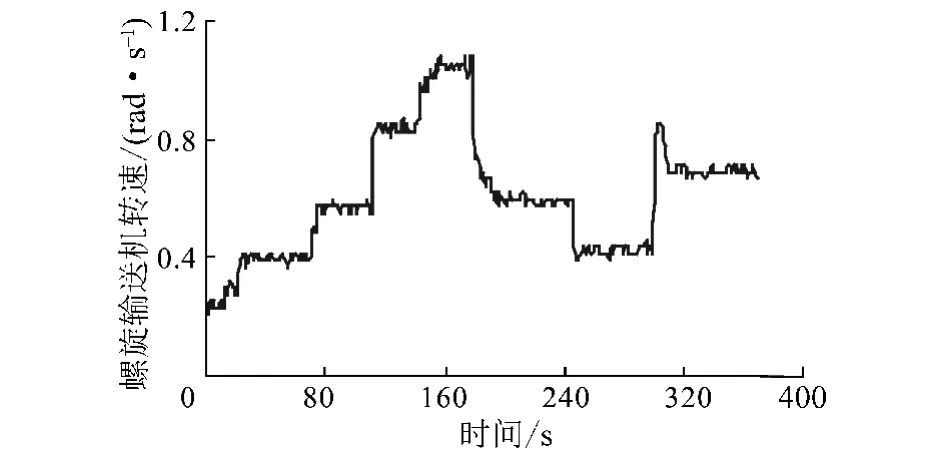
图4 螺旋输送机转速随时间的变化Fig．4 Variation of conveyor rotation speed versus time

图5 土仓压力随时间的变化Fig．5 Variation of chamber pressure versus time

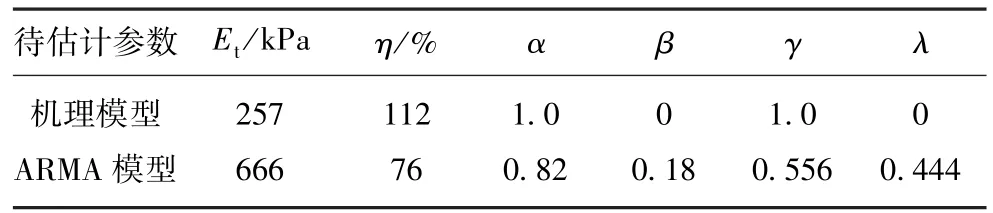
表1 系统模型参数辨识结果Table 1 Identified model parameters for different model

从表1可以看出,线性机理模型所得到的螺旋输送机排土效率大于100%,很显然是不尽合理的。模型参数α和γ表征了土仓压力平衡系统的线性部分,该线性部分正是线性机理模型所表征的。模型参数β和λ表征了该系统的时滞部分,此部分恰恰是ARMA模型所特有的,参数β和λ的引入将会显著提高模型的预测精度。从该4个参数的大小对比可以发现,螺旋输送机的转速对土仓压力平衡系统影响的时滞特性更加明显,进一步揭示了该系统时滞特性的物理本质。与盾构机的直径相对比,螺旋输送机直径小一个数量级,改变螺旋输送机的转速并不能立即改变土仓压力,而是需要又一个滞后过程,这也就是ARMA模型能够比较准确表征土仓压力平衡系统特性的原因所在。

如图6所示,机理模型拟合最大相对误差48%,预测最大相对误差41%。ARMA模型拟合最大相对误差14%,预测最大相对误差9%,新模型明显提高了拟合和预测精度。

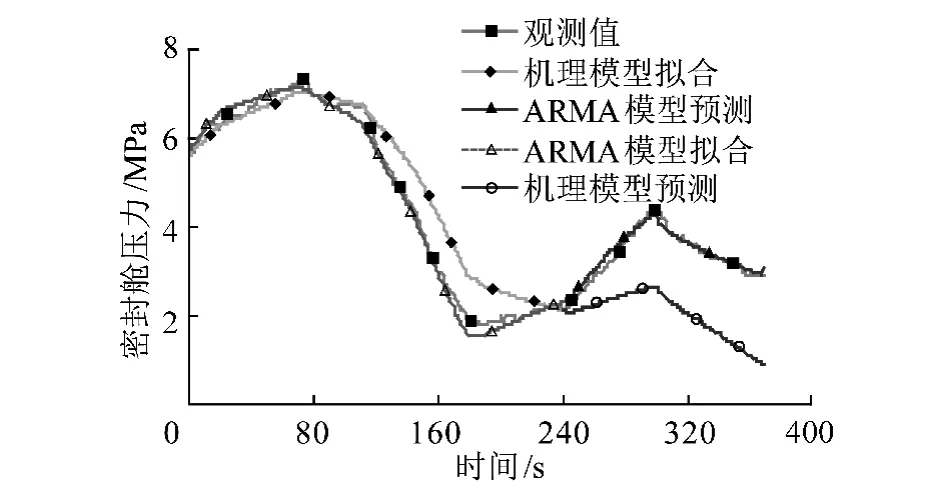
图6 土仓压力预测值与观测值的对比Fig．6 Comparison between forecast pressure and observed pressure

4 结 论

(1)土压平衡盾构机土仓压力平衡系统的工作性态表现出较强的时滞特征,简单的线性模型无法精确表征该动力系统的时滞特性,ARMA模型为解决这一课题提供了新的途径。

(2)实验结果表明,线性机理模型拟合的最大相对误差为48%,预测最大的相对误差为41%。ARMA模型拟合最大相对误差为14%,预测最大相对误差为9%。与经典的线性机理模型相对比,ARMA模型的拟合精度和预测精度得到了显著的提高,盾构机土仓压力平衡系统的ARMA模型精确地表征了该系统的时滞特性。

(3)模型参数α和γ表征了土仓压力平衡系统的线性部分,该线性部分正是线性机理模型所表征的。模型参数β和λ表征了该系统的时滞部分,此部分恰恰是ARMA模型所特有的,参数β和λ的引入将会显著提高模型的预测精度。与盾构机的直径相对比,螺旋输送机直径小一个数量级,改变螺旋输送机的转速并不能立即改变土仓压力,而是需要又一个滞后过程,这也就是ARMA模型能够比较准确表征土仓压力平衡系统特性的本质所在。

(4)尽管ARMA模型给出了较高的土仓压力拟合和预测精度,但是该模型并没有考虑到该系统的时变性、非线性和随机性。渣土的等效变形模量和螺旋输送机的排土效率可能是土仓压力的函数,同时盾构机掘进过程中地质条件随机变化,如何考虑这些复杂因素的影响进行土压平衡系统建模是本课题进一步深入研究的内容。

[1] 刘宣宇,邵 诚,刘东昭．基于密封舱压力场梯度的盾构开挖面稳定性判定[J]．煤炭学报,2012,37(10):1463-1468．

Liu Xuanyu,Shao Cheng,Liu Dongzhao．Stability judgment of shieldexcavation face based on earth pressure field gradient in pressure chamber[J]．Journal of China Coal Society,2012,37(10):1463-1468．

[2] 李守巨,曹丽娟．盾构机土仓压力控制模型及其参数辨识[J]．煤炭学报,2012,37(2):206-210．

Li Shouju,Cao Lijuan．Pressure control model on soil chamber of shield machine and its parameter identification[J]．Journal of China Coal Society,2012,37(2):206-210．

[3] Xu Qianwei,Zhu Hehua,Ding Wenqi．Laboratory model tests and field investigations of EPB shield machine tunneling in soft ground in Shanghai[J]．Tunneling and Underground Space Technology, 2011,26(1):1-14．

[4] Yang Huayong,Shi Hu,Gong Guofang,et al．Electro-hydraulic proportional control of thrust system for shield tunneling machine[J]．Automation in Construction,2009,18(7):950-956．

[5] 施 虎,杨华勇,龚国芳．盾构掘进机关键技术及模拟试验台现状与展望[J]．浙江大学学报(工学版),2013,47(5):741-749．

Shi Hu,Yang Huayong,Gong Guofang．Key technologies of shield tunneling machine and present status and prospect of test rigs for tunneling simulation[J]．Journal of Zhejiang University(Engineering Science),2013,47(5):741-749．

[6] 王洪新．土压平衡盾构刀盘开口率对土舱压力的影响[J]．地下空间与工程学报,2012,8(1):89-93．

Wang Hongxin．Influence of aperture ratio of cutterhead of EPB shield on earth pressure in the chamber[J]．Chinese Journal of Underground Space and Engineering,2012,8(1):89-93．

[7] 施 虎,龚国芳,杨华勇．盾构掘进土压平衡控制模型[J]．煤炭学报,2008,33(3):343-346．

Shi Hu,Gong Guofang,Yang Huayong．Control model of earth pressure balance for shield tunneling[J]．Journal of China Coal Society, 2008,33(3):343-346．

[8] 夏毅敏,卞章括,暨智勇,等．复合式土压平衡盾构刀盘CAD系统开发[J]．计算机工程与应用,2012,48(36):64-69．

Xia Yimin,Bian Zhangkuo,Ji Zhiyong,et al．Development of cutter head CAD system for composite EPB shield[J]．Computer Engineering and Applications,2012,48(36):64-69．

[9] Yao Guoyu,Ding Ruifeng．Two-stage least squares based iterative identification algorithm for controlled autoregressive moving average (CARMA)systems[M]．Computers and Mathematics with Applications,2012,63:975-984．

[10] Erasmo Cadenas,Wilfrido Rivera．Wind speed forecasting in three different regions of Mexico,using a hybrid ARIMA-ANN model [J]．Renewable Energy,2010,35:2732-2738．

[11] Ma Lei,Luan Shiyan,Jiang Chuanwen．A review on the forecasting of wind speed and generated power[J]．Renewable and Sustainable Energy Reviews,2009,13:915-920．

[12] Volkan S,Edigera,Sertac Akar．ARIMA forecasting of primary energy demand by fuel in Turkey[J]．Energy Policy,2007,35:1701-1708．

[13] 王 锋,李宏光,臧 灏．基于Logistic和ARMA模型的过程报警预测[J]．化工学报,2012,63(9):2941-2947．

Wang Feng,Li Hongguang,Zang Hao．Process alarm prognosis based on Logistic and ARMA models[J]．CIESC Journal,2012,63 (9):2941-2947．

[14] 孙书利,刘丽芳．具有随机多丢包的ARMA信号最优线性估计[J]．控制与决策,2013,28(2):223-228．

Sun Shuli,Liu Lifang．Optimal linear estimation for ARMA signals with stochastic multiple packet dropouts[J]．Control and Decision, 2013,28(2):223-228．

[15] 王红瑞,高 雄,钱龙霞．基于ARMA-GARCH模型的水文过程不确定性分析[J]．中国科学:技术科学,2012,42(9):1069-1080．

Wang Hongrui,Gao Xiong,Qian Longxia．Uncertainty analysis of hydrological processes based on ARMA-GARCH model[J]．Scientia Slnica Technologica,2012,42(9):1069-1080．

Autoregressive moving average model and its parameter estimation for earth pressure balance system of shield

LI Shou-ju1,HUO Jun-zhou2,CAO Li-juan3
(1.State Key Laboratory of Structural Analysis for Industrial Equipment,Dalian University of Technology,Dalian 116023,China 2.School of Mechanical Engineering,Dalian University of Technology,Dalian 116023,China 3.School of Mechanical and Power Engineering,Dalian Ocean University,Dalian 116023,China)

In order to characterize time delaying property and increase forecasting precision of earth pressure balance system of shield,an autoregressive moving average(ARMA)model was proposed．Based on optimization algorithm,parameter estimation procedure was presented to determine ARMA model parameters．The experimental investigation shows that compared with classic mechanism model,ARMA model obviously increases fitting and forecasting precisions．The maximum relative error of computed earth pressure falls from 41%to 9%forecasted by ARMA model．According to experimental data,the time delaying properties of the dynamic response of the system was discussed．The affection of past rotating speed of conveyor on earth pressure on next time is more obvious．

autoregressive moving average model;parameter estimation;earth pressure balance system;shield;time delaying property

TD263

A

0253-9993(2014)11-2201-05

2013-10-10 责任编辑:常 琛

国家重点基础研究发展计划(973)资助项目(2013CB035402);国家自然科学基金重点资助项目(51105048);工业装备结构分析国家重点实验室开放基金资助项目(S14206)

李守巨(1960—),男,辽宁沈阳人,教授,博士。E-mail:lishouju@dlut．edu．cn

李守巨,霍军周,曹丽娟．盾构机土压平衡系统的ARMA模型及其参数估计[J]．煤炭学报,2014,39(11):2201-2205．

10．13225/j．cnki．jccs．2013．1470

Li Shouju,Huo Junzhou,Cao Lijuan．Autoregressive moving average model and its parameter estimation for earth pressure balance system of shield[J]．Journal of China Coal Society,2014,39(11):2201-2205．doi:10．13225/j．cnki．jccs．2013．1470