谐波式齿轮泵柔轮强度分析

潘俊，祝海林，潘月仙，吴宏能

(常州大学机械工程学院，江苏常州 213016)

随着国民经济的发展，液压传动已经得到越来越多行业的重视，而齿轮泵作为液压传动系统中比较常见的一种液压元件，现已广泛应用于机床、冶金、矿山、建筑、船舶等机械产品的液压系统中［1］。

谐波式齿轮泵是在内啮合齿轮泵的基础上采用谐波齿轮传动代替原有内啮合齿轮传动的一种新型齿轮泵，它不仅保留了内啮合齿轮泵结构紧凑、相对滑动速度小、流量脉动小、容积效率高等优点［2］，还具有谐波齿轮传动承载能力大、传动比大、传动精度高、回差小等优点［3］，并且解决了普通齿轮泵径向力不平衡的问题。谐波式齿轮泵工作时，柔轮会不断地发生弹性变形，从而使得柔轮极易产生疲劳破坏，直接影响泵的使用寿命，因此，对柔轮进行强度分析十分必要。

1 谐波式齿轮泵工作原理

谐波式齿轮泵工作原理如图1所示，在刚轮与柔轮之间用月牙挡板隔开，这样便形成4个密封的工作腔，当波发生器固定，刚轮按照图1所示方向转动时，柔轮也按同一方向转动。随着吸油口处刚轮与柔轮轮齿的脱开，密封的工作腔体积增大形成真空，使得外界压力大于内部压力，油液便在大气压作用下经吸油口进入吸油腔，并逐渐充满轮齿间隙。当吸油腔充满油液后，油液便随着齿轮的转动被带入压油腔，此时压油口处刚轮与柔轮的轮齿正逐渐进入啮合，使得工作腔体积减小，从而形成了高压油腔，齿间的油液便通过压油口被挤出，输送到液压传动系统中。

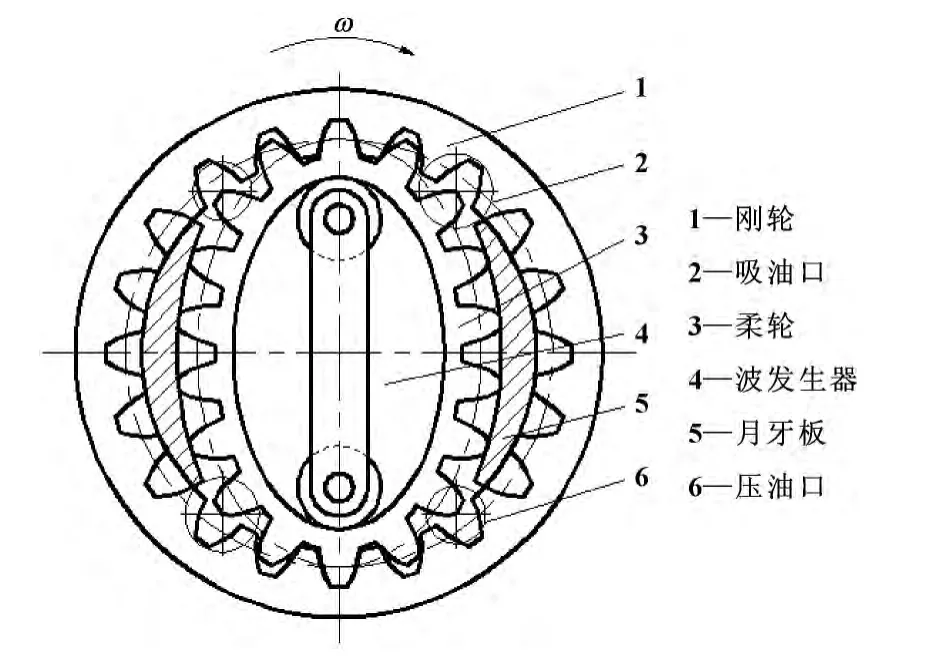
图1 谐波式齿轮泵原理简图

2 柔轮疲劳强度分析

2.1 柔轮的变形及应力分析

如图2所示，柔轮受到双滚轮波发生器两个对称的径向力作用而发生变形，且在B、D两点处出现最大正应力σmax，A、C两点处出现最小正应力σmin。

柔轮转动时，实际由弯曲正应力σ和扭转切应力τ共同作用，但是由于谐波式齿轮泵的柔轮采用环形结构，不存在筒形柔轮从轮齿部分到光滑部分过渡时因横截面形状改变而产生的扭转切应力集中现象［4］，因此，扭转切应力τ对谐波式齿轮泵柔轮疲劳强度的影响很小，在近似计算中，可以只考虑弯曲正应力σ的影响。一般情况下，对谐波式齿轮泵柔轮进行疲劳强度分析，即确定它的疲劳强度安全系数是否满足要求:

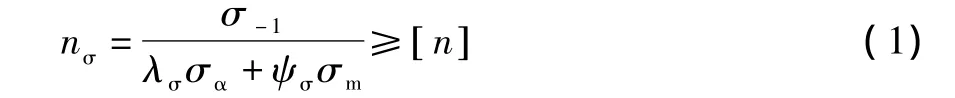
式中:σ-1为柔轮材料的弯曲疲劳强度极限，MPa;

λσ为实际柔轮与样件的疲劳极限差异系数，一般取 1.8 ～2［5］;

ψσ为平均应力影响系数，一般取0.1～0.15［5］;

σα为柔轮截面上的循环应力幅值;

σm为柔轮截面上的平均应力;

［n］为柔轮材料许用安全系数，一般取1.3～1.5［5］。

其中［4］:

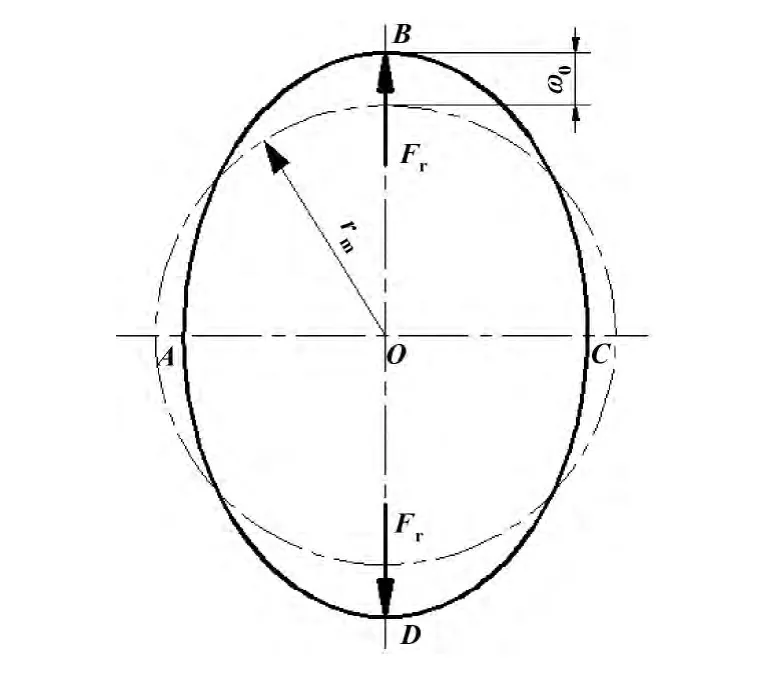
图2 柔轮变形示意图

2.2 柔轮疲劳强度校核

根据材料力学中有关变形和应力公式，采用莫尔积分可得谐波式齿轮泵环形柔轮长轴的直径增大量为［6］:

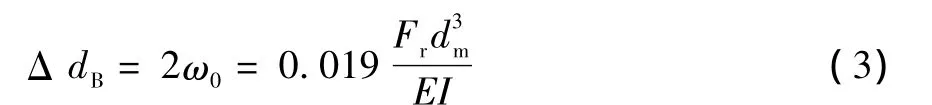
即可得径向力为:

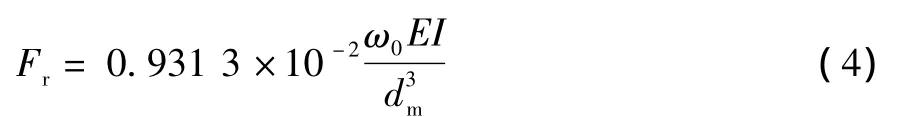
式中:ω0为柔轮最大径向变形量，mm;

E为柔轮材料的弹性模量，对于钢，E=2.1×105N/mm2［6］;

dm为柔轮中性圆直径，mm;dm=df-δ(df为柔轮齿根圆直径，δ为柔轮壁厚)

在径向力作用下，B、D两点的弯矩为:

由公式 (4)和 (5)可得最大正应力为:

式中:Kδ为柔轮上的轮齿影响系数，一般取1.05～1.1［6］。

同理可得最小正应力为:

由公式 (6)和 (7)可得:

将公式 (8)代入公式 (1)，并取 λσ=1.8［5］，ψσ=0.15［5］，Kδ=1.05［6］，=0.9［6］，可得谐波式齿轮泵柔轮疲劳强度校核公式为:

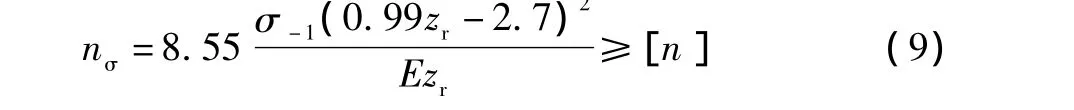
3 柔轮轮齿弯曲强度分析

3.1 柔轮轮齿最大弯矩分析

谐波式齿轮泵柔轮受载时，齿根所受的弯矩最大，因此齿根处的弯曲疲劳强度最弱。当载荷作用于齿顶时，此时弯矩的力臂虽然最大，但是力并非最大，因此弯矩并不是最大。根据分析，柔轮齿根所受的最大弯矩发生在啮合点位于单对齿啮合区最高点处，即如图3所示齿面法向力Fn作用于柔轮分度圆处，因为此时Fn与轮齿对称中心线的垂线的夹角β刚好等于分度圆压力角α，从而使得齿面法向力Fn用于产生弯曲应力的分力达到最大，因此，齿根弯曲强度校核也应按载荷作用于单对齿啮合区最高点来计算。

根据机械原理，将轮齿看作悬臂梁，如图3所示，齿面法向力Fn与轮齿对称中心线的垂线的夹角为β，F1与F2为Fn的两个分力，F1使齿根产生弯曲应力，F2则产生压应力，因此，柔轮齿根危险截面的弯曲力矩为［7］:

式中:K为载荷系数，当原动机为电动机时，一般取1.2 ～ 1.6［7］;

Fn为齿面法向力，N;

β为法向力与轮齿对称中心线的垂线的夹角;

h1为单对齿啮合区最大力臂，mm;

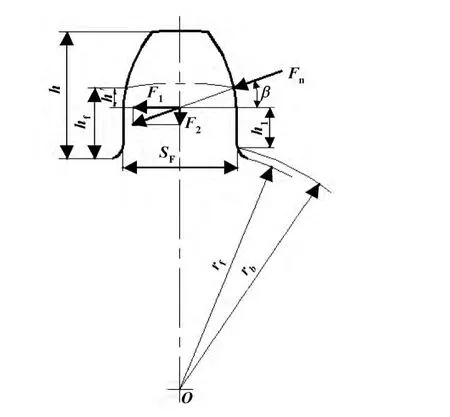
图3 柔轮轮齿受力示意图

法向力Fn可用以下关系式表示:

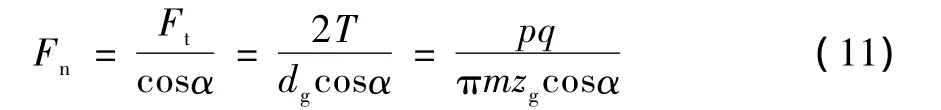
式中:Ft为齿轮圆周力，N;

T为泵的输入转矩，N·mm;

p为泵的出口压力，MPa;

q为泵的排量，mL/r;

m为齿轮模数，mm;

zg为刚轮齿数;

α为分度圆压力角。

如图3所示，单对齿啮合区最大力臂h1可用以下关系式表示:

式中:zr为柔轮齿数。

将公式 (11)、(12)代入公式 (10)可得柔轮轮齿最大弯矩为:

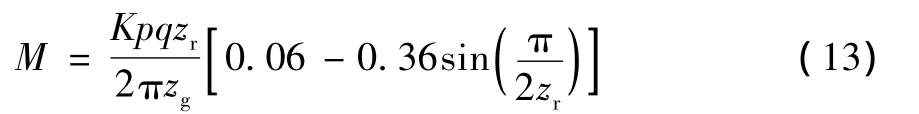
3.2 柔轮轮齿弯曲强度校核

柔轮轮齿的危险截面可看作是一个宽为b、高为SF的长方形，因此，其截面惯性矩为［8］:

式中:b为柔轮齿宽，mm;

SF为柔轮轮齿危险截面的高，mm。

为方便计算，可将SF视为柔轮基圆处齿厚对应的弦长，根据任意圆上的齿厚公式可得基圆处齿厚为［9］:

式中:rb为柔轮基圆半径，mm;

r为柔轮分度圆半径，mm;

αb为基圆压力角。

根据任意圆上的压力角公式可得基圆压力角为［9］:

将公式 (16)代入公式 (15)可得:

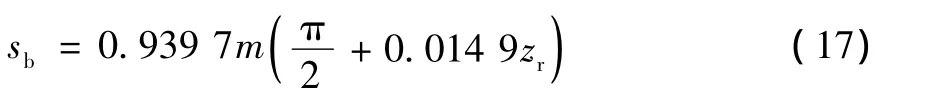
因此，柔轮基圆处齿厚对应的弦长为:

由公式 (13)、(14)和 (18)可得柔轮轮齿弯曲强度校核公式为:

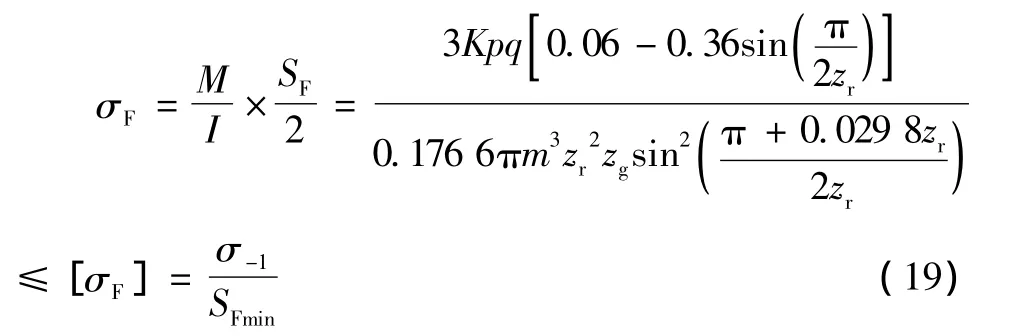
式中:［σF］为许用安全应力，MPa;

σ-1为柔轮材料的弯曲疲劳强度极限，MPa;

SFmin为最小安全系数，塑性材料一般取1.5～2。

4 实例分析

现有一谐波式齿轮泵，出口压力p=4 MPa，排量q=630 L，柔轮材料为30CrMnSiA，热处理方式为调质+氮化，弯曲疲劳极限σ-1=620 N/mm2，最小安全系数SFmin=1.8，弹性模量E=2.1×105MPa，柔轮齿数zr=70，刚轮齿数zg=72，模数m=4 mm，载荷系数K=1.6。

将上述数据分别代入公式 (9)和 (19)可得:

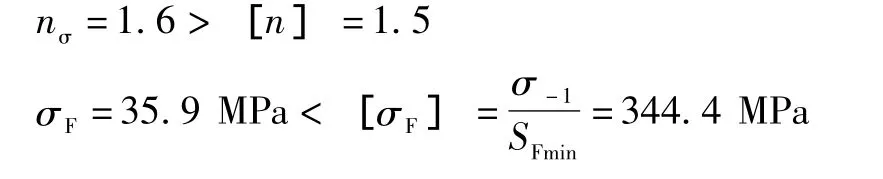
因此，柔轮满足疲劳强度要求和轮齿弯曲强度要求。

5 结论

随着机械行业的发展，齿轮泵作为液压传动系统中常见的一种液压元件，必将得到越来越广泛的应用。谐波式齿轮泵作为一种新型齿轮泵，解决了径向力不平衡这一问题，在未来的社会发展中一定会起到重要作用。文中推导出的柔轮疲劳强度校核公式和轮齿弯曲强度校核公式，可校核柔轮是否满足强度要求，为新型齿轮泵的设计和开发提供了理论参考。

［1］章宏甲，王积伟，黄谊.液压与气压传动［M］.北京:机械工业出版社，2005.

［2］栾振辉.齿轮泵研究的现状与发展［J］.起重运输机械，2005(6):11-13.

［3］王长明，阳培，张立勇.谐波齿轮传动概述［J］.机械传动，2006，30(4):86-88.

［4］［苏］金茨勃格.谐波齿轮传动 -原理、设计与工艺［M］.汪福敏，孙行文译.北京:国防工业出版社，1982.

［5］［苏］伊万诺夫.谐波齿轮传动［M］.沈允文，李克美，译.北京:国防工业出版社，1987.

［6］饶振纲.行星传动机构设计［M］.北京:国防工业出版社，1994.

［7］杨可桢，程光蕴，李仲生.机械设计基础［M］.北京:高等教育出版社，2006.

［8］刘鸿文.材料力学［M］.北京:高等教育出版社，2004.

［9］郑文玮，吴克坚.机械原理［M］.北京:高等教育出版社，1997.