一种新型4自由度并联机构的参数优化及其应用研究

杨明星，郭宗和，王德军，崔荣江

(1.山东理工大学，山东淄博 255049；2.山东省农业机械科学研究所，山东济南 250100)

空间四自由度并联机构较Steward等并联机构结构简单、造价低，同时比三自由度并联机构具有较多的自由度等优点，是国内外研究并联机构的重要类型之一。CARRICATO［1］提出了一种完全各向同性的四自由度并联机构，并对此机构进行了运动学分析和实时控制研究。GOGU［2］介绍了无奇异完全各相同性的T2R2型四自由度并联机器人，分析验证了操纵器有很好的运动传输能力。黄真等人［3］提出了一种新型4-RPTR并联机器人机构，求出机构的位置正解并绘制了对应的三维机构装配简图。马履中等［4］研究一种新型3T-1R四自由度并联机器人机构，运用正交遗传算法对机构的工作空间进行优化设计。赵铁石等［5］基于螺旋理论综合出三移一转四自由度双重驱动并联机构。伞红军等［6］提出一种新型2-TP/2-TPS空间4自由度并联机构，运用约束螺旋理论对机构的运动性质和奇异位形进行分析研究。游达章等［7］设计了一种可实现三平移一转动的四自由度并联机构，分析了其工作空间的设计原理及过程。季晔等人［8］以各性能指标在任务空间内变化较小且分布均匀为目标，对4-UPU四自由度并联机构进行优化得到最佳的机构参数。

2-RPC/2-SPC并联机构是作者所在课题组提出的［9］一种新型空间4自由度并联机构，该机构可以实现三维移动和绕着y轴的转动。本文作者对该并联机构进行了运动学分析，给出约束条件的基础上以机构的运动空间最大为目标函数对机构进行优化，对优化的结果运用Adams软件验证了该机构在减震平台上的应用。

1 机构的运动学分析

1.1 2-RPC/2-SPC并联机构模型的建立

2-RPC/2-SPC并联机构如图1所示，该并联机构由动平台B1B2B3B4，定平台A1A2A3A4以及连接两平台的4个支链组成，其中1、3支链为对称布置且由结构相同的R-P-C副组成，2、4支链为对称布置且由结构相同的S-P-C组成。动平台和定平台均为矩形，且与1、3支链相连的动、定平台长度分别为a、d，与2、4支链相连的动、定平台长度分别为b、c。根据该机构的特点，建立定坐标系O-XYZ在定平台的中心位置O上，动坐标系p-xyz在动平台的重心位置p上。通过驱动纵向移动副Pi改变支链SiCi的长度和转向，从而实现动平台位姿的变化。

图1 2-RPC/2-SPC并联机构简图

1.2 机构的自由度计算

机构的第2、4支链布置相同且都为无约束支链，只需对该机构的第1、3支链进行螺旋分析。现取图2所示机构的支链1进行分析，可得:

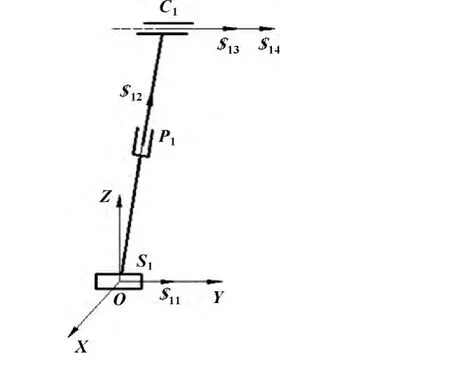
图2 支链1螺旋系的建立

根据螺旋理论中运动螺旋与约束螺旋之间的互易关系，可求得RPC支链约束反螺旋为两力偶:

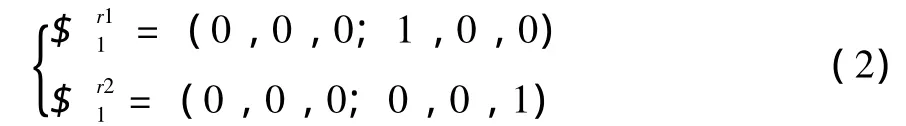
因1、3两条RPC支链平行布置，可知:

根据线矢在共轴条件下最大线性无关数为1，则机构

约束螺旋系仍为两力偶:

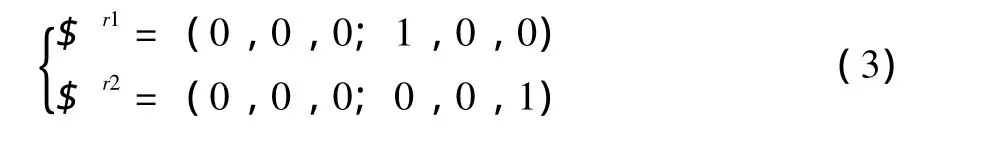
基于以上分析，由于机构约束反螺旋为两力偶，约束了动平台绕X轴和Z轴的旋转运动，所以机构可以实现三平移和绕Y轴转动。

1.3 机构的位置反解

位置反解可以简单的描述为:已知动平台的位姿(xP，yP，zP，β)，求解纵向连杆的杆长Li。选择RPY(绕固定轴Z-X-Y旋转)坐标表示法描述姿态旋转矩阵，定义首先将动坐标系绕定坐标系的Z轴旋转α角，再绕定坐标系的Y轴旋转β角，最后绕定坐标系的X轴旋转γ角。由于α=γ=0则两坐标系之间的变换矩阵为:

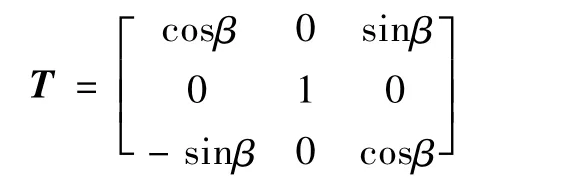
则:R=TR0+P

式中:R为动平台上一点在静坐标系中的坐标;

R0为动平台上一点在动坐标系中的坐标;

P为动平台中心点p在静坐标系中的坐标。

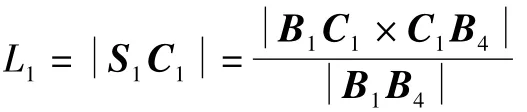
同理，可求得另外3个杆长

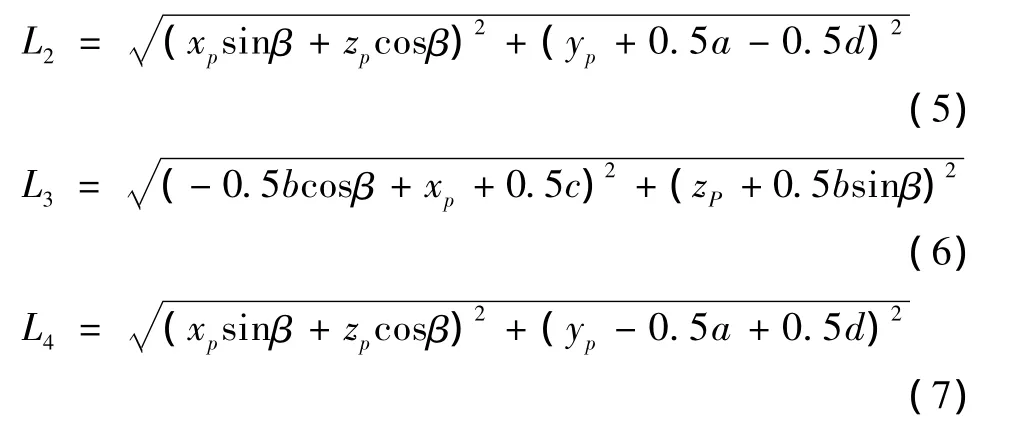
对于已知动平台的位姿，则由公式 (4)— (7)可以求出纵向的4个驱动杆长，即求得机构的位置反解。

1.4 机构的雅克比矩阵及其奇异性

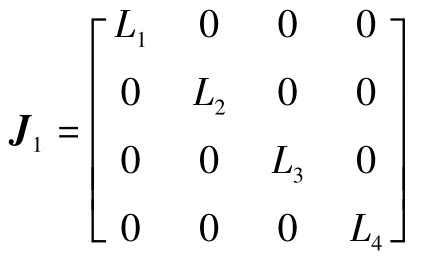
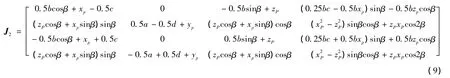
这里，J为动平台位姿速度对各支链输入速度的一阶影响系数矩阵，即通常所说的Jacobian矩阵。

可以看出，机构的逆雅克比矩阵J1的行列式不可能为0，故以正雅克比矩阵J2为基础，对该机构的奇异位型进行分析。令det(B)=0，整理得

由式 (10)可求得机构发生位形奇异的情况:

(1)当d－a=0时，即第1、3支链与动、定平台相连处的尺寸相同，在实际中这种奇异位型是可以避免的。

(2)当xpsinβ+zpcosβ=0时，用Mathematica绘图得，机构处于奇异位型时的点，如图3所示。

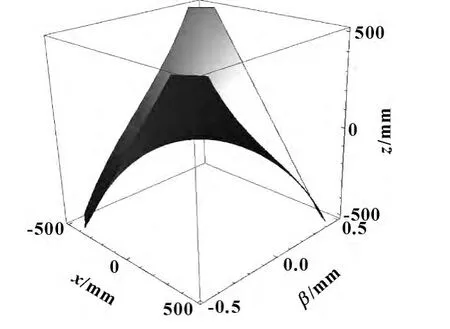
图3 机构奇异位形图

针对这种奇异情形，在进行机构轨迹规划时要尽量避免出现的奇异点。

(3) 当zp(xpcosβ－zpsinβ)+0.25bsinβ(b－ccosβ)=0时，机构出现的奇异位型与机构的尺寸和轨迹点同时有关，这就要求我们根据实际情况合理的进行尺寸选取和轨迹规划。

2 2-RPC/2-SPC并联机构参数优化及结果分析

2.1 机构的参数优化函数的建立

在实际的问题中，希望所设计的结构参数尽可能地使整个机构具有较大空间，并且希望整体机构的驱动性能较好。因此，选取机构参数优化的目标函数、设计变量、约束条件如下:

(1)目标函数:

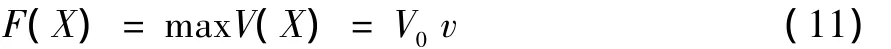
其中，v=Aw/A0，使用蒙特卡洛方法［12］求解并联机构的工作空间符合条件的采样点空间Aw与采样空间点集A0的比值v(也称相对体积)，V0为选定空间的体积。

(2)设计变量:

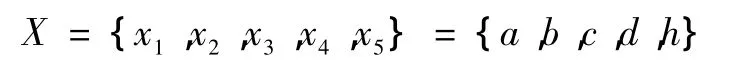
其中:a、b分别为动平台的长和宽;c、d分别为定平台的长和宽，h为动、定平台的初始高度差。

(3)约束条件:根据整体结构尺寸及布置的可能性要求，在设计中给出个设计变量的允许变化范围，可以表示为:s.tlb≤X≤ub其中，lb为变量下限，ub为变量上限。

2.2 优化实例

根据2-RPC/2-SPC并联机构自身的结构特点可知，设动平台的尺寸为a=150 mm，b=140 mm，则影响该机构性能的因素主要有以下几个方面:

(1)定平台的整体尺寸c、d，以及动、定平台的初始高度差h。

(2)纵向移动副滑移量限制。从并联机构的应用出发，绝大多数并联机构各分支杆的滑移长度变化是有范围的。这里假设机构的4个纵向连杆的杆长Li相对初始杆长L0的滑移量Si;位移最大量为Smax，则机构在运动中应符合的条件是-Smax≤Si≤Smax

(3)转动副和球副的转角限制。转动副和球副在连接机构连杆的同时，也要求转角不能随意转动，必须符合设计的要求。这里定义纵向连杆与竖直方向的夹角为 θi，夹角允许的最大值为 θmax，最小值为θmin，则 θi应满足的条件是:θmin≤θi≤θmax机构参数的约束条件为:

2.3 优化结果及分析

为了研究方便，分别取定平台的长c、宽d以及动、定平台的初始高度差h这三个参数中的一个为变量，其余2个为常数进行分析，得到结果如图4所示。

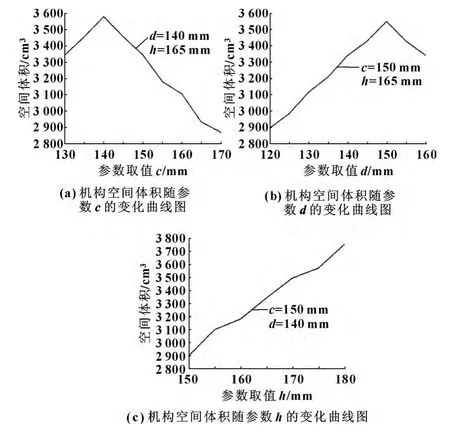
图4 结构参数与工作空间关系

可以看出，随着定平台的尺寸增大，机构的工作空间先增大后减小;并且当与动、定平台相连的同一支链的对应尺寸相同时，机构的工作空间达到最大值。同时，当想让机构达到更大工作空间时，在满足一定空间和性能的情况下尽量使初始动、定平台的高度差尽可能大些。

3 仿真验证及结论

3.1 仿真验证

图5 2-RPC/2-SPC并联机构的仿真模型

在希望机构运动空间较大的同时尽量避免因结构参数带来位形奇异，期望机构有较好的运动学性能。基于以上分析，设想把该并联机构用于减震平台，选取机构的结构参数为a=150 mm，b=140 mm，c=140 mm，d=140 mm，h=170 mm在 ADAMS环境下建立的2-RPC/2-SPC并联机构减震平台模型，如图5所示。

为了验证减震效果，取动平台的质量为20 kg，在纵向连杆移动副处添加k=10.0 N/mm、阻尼系数为c=2.0 N·s/mm的阻尼弹簧，并且对动平台中心施加x、y、z3个方向的脉冲力F和绕着y向脉冲力矩M，力的幅值为500 N，力矩幅值为500 N·mm，脉冲总时间都为0.4 s，脉冲函数为:STEP(time，0，0，0.1，500)+STEP(time，0.1，500，0.3，-500)+STEP(time，0.3， -500，0.4，0)，进行End Time=10、steps=100的动力学仿真，可以得到在脉冲激励下，动平台的加速度随时间变化的曲线。如图6所示，横坐标为时间 (单位s)，纵坐标为加速度 (单位mm/s2)，由曲线可以看出动平台的加速度有明显的衰减，因此该机构可以实现很好的减震性能。

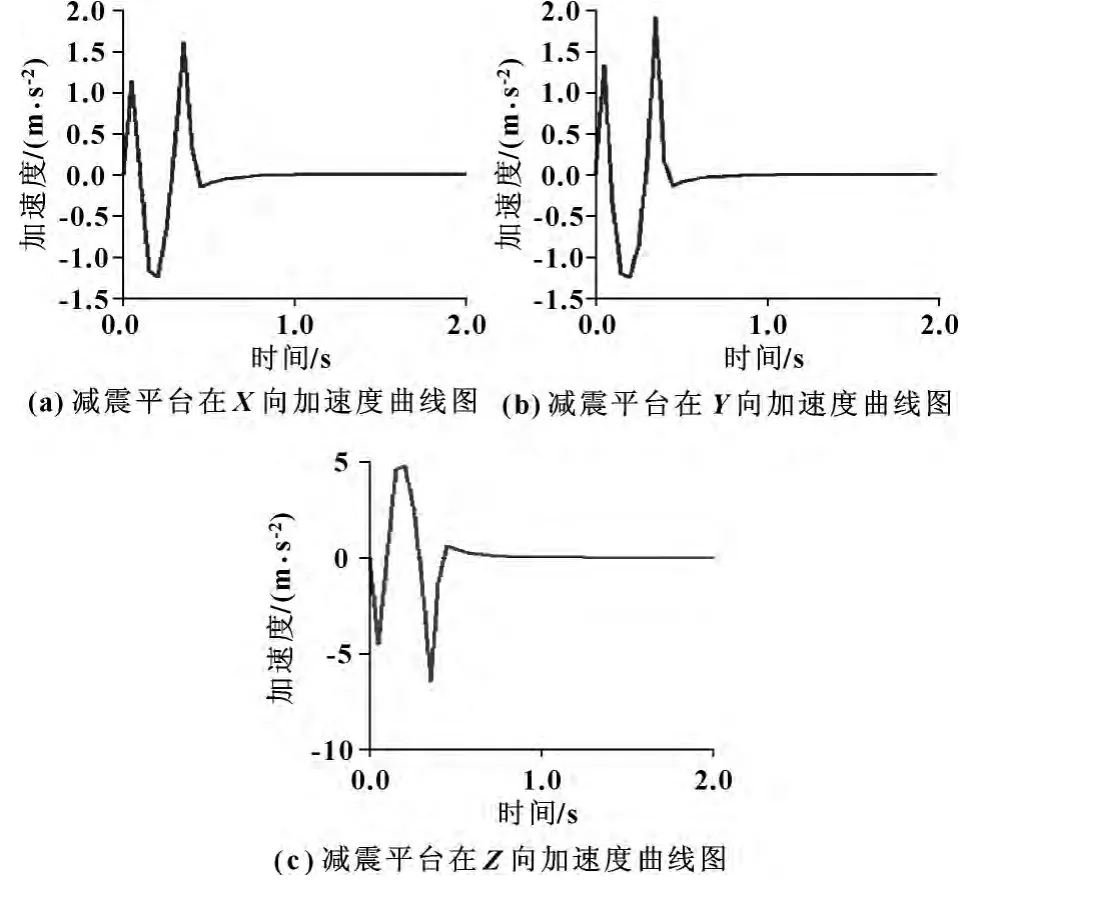
图6 减震平台的加速度曲线图

3.2 结论

(1)对2-RPC/2-SPC并联机构进行了运动学分析，求得了该机构的位置反解、速度雅克比矩阵并进行了奇异性分析，为该新型并联机构的研究提供了理论基础。

(2)给出约束条件的基础上以机构的工作空间最大为目标函数，优化出最佳尺寸参数，仿真验证了优化结果在并联机构减震平台的应用，对该机构的其他应用具有重要参考的价值。

［1］CARRICATO Marco.Fully Isotropic Four-degrees-of Freedom Parallel Mechanisms for Schoenflies Motion［J］.International Journal of Robotics Research，2005，24(5):397-414.

［2］GOGU Grigore.Fully-isotropic Parallel Robots with Four Degrees of Freedom T2R2-Type［R］.International Conference on Intelligent Robots and Systems，IROS，2005:1190-1195.

［3］张立杰，李永泉，黄真.一种4自由度并联机器人的位置正解分析［J］.机械设计与研究，2006，22(4):21-24.

［4］马晓丽，马履中，周兆忠，等.3T-1R并联平台的工作空间分析与优化设计［J］.中国机械工程，2006，17(18):1938-1943.

［5］李宁宁，赵铁石，边辉.双重驱动四自由度并联机构型综合［J］.机械设计与研究，2008，24(1):51-54.

［6］伞红军，钟诗胜，王知行.新型2-TPR/2-TPS空间4自由度并联机构［J］.机械工程学报，2008，44(11):298-303.

［7］XU Zhenda，YOU Dazhang.Design and Simulation of a Type of Four Degrees of Freedom Parallel Robot［J］.Applied Mechanics and Materials，2012:229-231.

［8］季晔，刘宏昭，原大宁，等.一种四自由度并联机构的指标分析［J］.中国机械工程，2012，23(3):258-263.

［9］郭宗和，崔荣江，杨启志，等.基于广义被动链的非对称3TnR并联机构的构型综合［J］.机械设计与制造，2012(7):242-244.

［10］何景峰，李保平，杨宏斌，等.Gough-Stewart机构的奇异性及其 ADAMS仿真验证［J］.机床与液压，2010，38(5):104-107.