双因素无重复的方差分析法
2014-06-05杨小勇
杨小勇
双因素无重复的方差分析法
杨小勇
(广东石油化工学院 化学与生命科学学院,广东 茂名 525000)
浅析了方差分析法的基本原理和方差分析的意义。方差分析就是将总的方差分解为各个方差的成分,再利用显著性检验法进行分析判断和做出适当的结论。通过例题详细地讲解、介绍了双因素的方差分析法,回答了学生在学习中经常提出的有关问题。
方差;方差分析法;双因素;无重复;判断
在实验教学过程中,常有学生问到这样的问题:若干个实验者利用若干种不同的分析方法测定某种试样的成分或每一参数,每一种分析方法都重复测定几次,如何判断分析方法之间和分析者之间对测定结果有无显著差异,哪一个平均值准确可靠。若要回答学生这些问题,则需运用方差分析法的有关知识。
在科学研究中,为了探索某一项分析任务的可靠性和影响因素,需要进行大量的实验[1]。例如,取几批试样分别送到几个相关的实验室用不同的方法进行实验,每一方法的测定又重复若干次,这样就得到大量数据。根据得到的这些数据,用什么方法可以判断哪一个因素对测定结果影响最大?哪一个因素影响不大?常用的方差分析法就是一种处理和判断数据的手段[2]。下面结合实例简单浅析方差分析法有关知识。
1 标准偏差和方差[3]
在数理统计中常用标准偏差表示精密度,标准偏差(简称“标准差”)或称均方误差,用σ代表,表达式为:
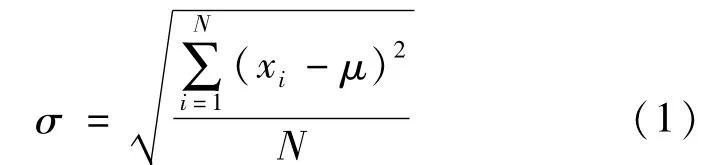
式(1)是应用于大量数据的条件下(一般有30次以上测定),这时,测定的平均值接近于真值,用μ表示;根式的分子代表各次测定数据的偏差的平方和,N是测定次数。方差代表各偏差平方和的平均值,用σ2表示。我们知道,只有当测定次数为无限多或者至少有30次以上时,所得的平均值称真值。但是,通常测定次数总是有限的,这样,所得的平均值并不是真值,这时,如果按式(1)计算标准偏差就不合理。
测定平均值与真值不相等,测定值与平均值之差同测定值与真值之差不相等。要表示有限测定次数的精密度,采用符号S代替σ,有限测定次数标准偏差的计算公式为:

与式(1)比较,用试样平均值x代替了真值μ,用N-1代替N。N-1在数理统计中称之为“自由度”,它说明在N次测定中,只有N-1个可变的偏差。自由度也可理解为:数据中可供对比的数目。例如,两次测定a和b,只有一个a与b之间的比较,若三次测定,可有两种比较(即其中任何两个数据之间及这两个数据的平均值与第三个数据之间比较),类推下来,N次测定只有N-1个可供对比。如果有几个互相独立的因素同时影响测定结果,设不同来源的方差分别为按方差的加和法则,总的方差σ2应为各个方差之和:
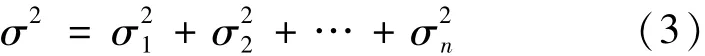
方差分析就是将总的方差分解为各个方差的成分,再利用显著性检验法进行分析判断和做出适当的结论[4]。方差分析有:(1)单因素的方差分析;(2)无重复双因素的方差分析;(3)具有重复(等重复、不等重复)双因素的方差分析;(4)三因素的方差分析。
2 双因素无重复的方差分析方法[5]
在无重复双因素的方差分析方法中有两个变动因素。设双因素试验中的两个变动因素为A和B,因素A有a个不同水平:A1,A2,…,Aa;因素B有b个不同水平:B1,B2,…,Bb,则因素A与因素B之间共有ab种不同的水平组合方式。对于两个因素的所有不同水平组合方式均进行试验,称为双因素全面试验。在每一种试验条件下均进行一次试验(r=1),称为双因素全面无重复试验,简称双因素无重复试验。
本文讨论双因素无重复方差分析,即几个分析(实验)者使用几种不同的方法去测定某种试样的成分(或某一参数),每一种方法都重复测定几次,把分析者和分析方法同时作为影响分析结果的因素来考虑,同时判断分析者之间和分析方法之间有无显著差异。
如果影响测定结果的因素不止一个而是两个,那么总的平方和应包括两种因素所引入的平方和及实验误差δ0的平方和:
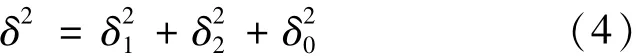
和单因素的方差分析方法一样,把平方和分解并计算平均平方,利用F检验[6]就能作出判断。
3 双因素无重复的方差分析方法例题分析[7]
例题:20.0℃,常压下,利用静力学原理,用四种不同方法测定0.005 c/(mol·L-1)正丁醇的液体表面张力,每种方法由五名不同实验者测定5次,所得数据见表1[8]。把分析方法和分析者同时作为影响分析结果的因素来考虑,同时判断分析方法之间和分析者之间对测定结果有无显著差异。
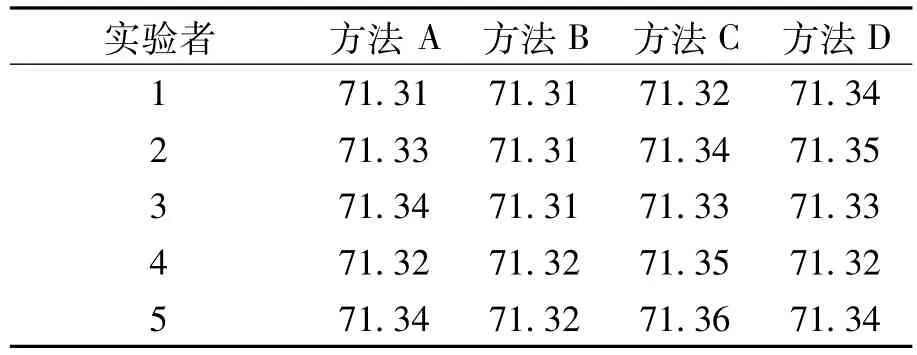
表1 测定数据 σ/10-3N·m-1
解:为了简化计算过程,将原数据减出71.31,表1数据转化为表2的数据。
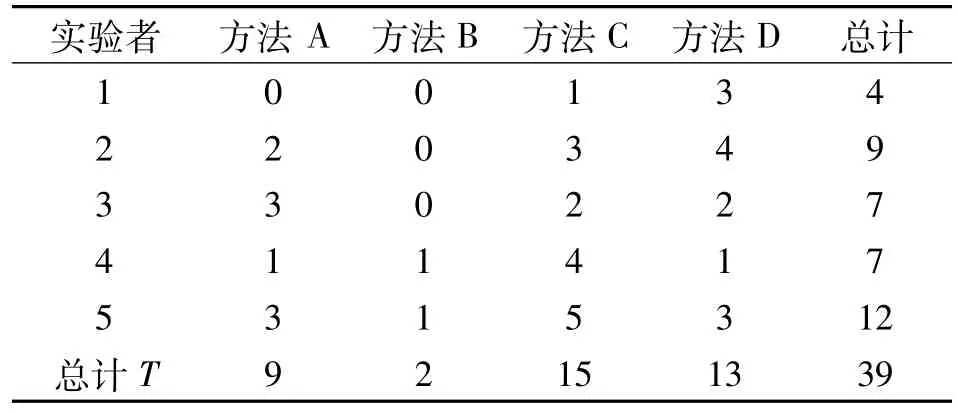
表2 测定数据 σ/10-3N·m-1
假如两个因素的影响是相互独立的,实验分析者这个因素自然影响每一种的总计值,但这应该是一个恒定的系统误差。方差分析的目的就是要检定判断出两个因素各自的影响,即求得实验分析方法之间及实验分析者之间的平均平方。方差分析见表3。
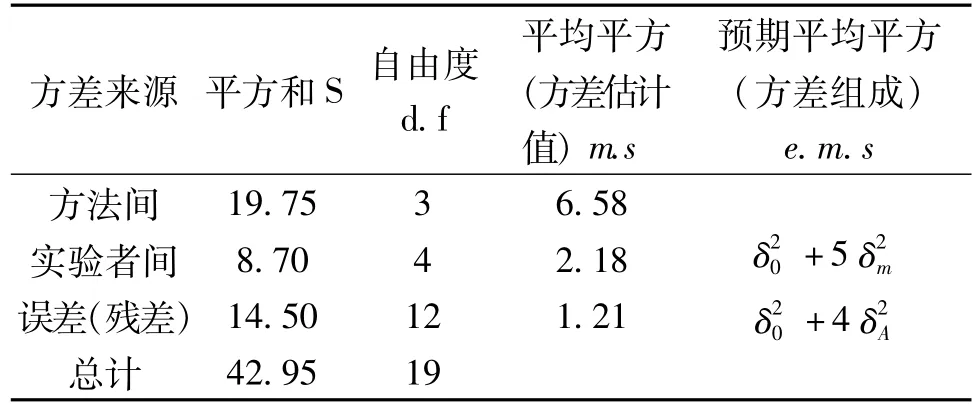
表3 方差分析表
3.1 计算步骤
计算步骤如下:
1)求校正因子CF

2)计算总S

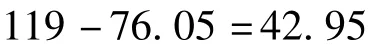
3)方法间的S
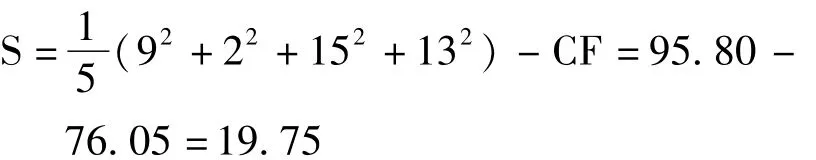
4)实验者间的S
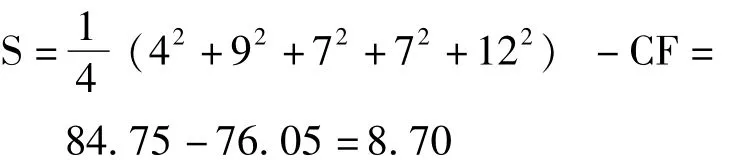
5)残差

6)自由度(d.f,方法间)=k-1=4-1=3
7)自由度(d.f,实验者间)=k-1=5-1=4
8)自由度(d.f,误差平方和)=自由度(d.f)方法间×自由度(d.f)实验间=3×4=12
3.2 检验
1)方法间
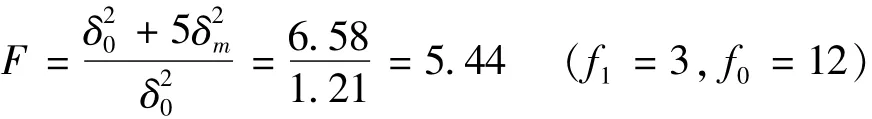
查F表得

2)实验者间
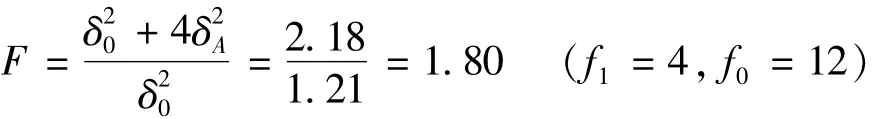
查F表得

由F检验的临界值
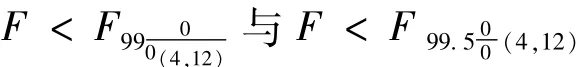
同时成立,判断实验者之间影响不显著,说明实验者之间不存在显著差异,可以判断每一个(实验者)平均值基本准确可靠。至此,双因素无重复的方差分析完毕。
4 结束语
在上述的例题中,每一方法和每一分析者均只进行过一次测定,不能反映出测定本身的误差。按上述计算所得的残差可能同时包含有真正偶然误差和交互效应,用这样的简单双因素方差分析不可能把真正偶然误差与交互效应区别开来。因此,在显著性检验中,把残差作为实验偶然误差的估量值来计算,是不够合理的。若要改善这点,可使用具有重复(等重复、不等重复)双因素的方差分析法,使两因素的交互效应可以容易地从试验误差中分离出来,即测定出交互效应的显著与否。
[1]任弘,章潮晖,王利群,等.运用方差分析法估价测量可靠性的探讨[J].北京体育大学学报,2004,27(3):359-360.
[2]东北师范大学.物理化学实验[M].2版.北京:高等教育出版社,1989:20.
[3]宋清.定量分析中的误差和数据评价[M].北京:人民教育出版社,1982:14-15.
[4]郭太安.方差分析法的简易算法[J].数理统计与管理,1987(6):36.
[5]辛益军.方差分析与实验设计[M].北京:中国财政经济出版社,2001:72-68.
[6]东北师范大学.物理化学实验[M].2版.北京:高等教育出版社,1989:21.
[7]宋清.定量分析中的误差和数据评价[M].北京:人民教育出版社,1982:110-112.
[8]杨小勇.方差分析法浅析——单因素的方差分析[J].实验科学与技术,2013,11(1):42.
Discussion of Variance Analysis:Double Factors-no Repeated Variance Analysis
YANG Xiaoyong
(College of Chemistry and Life Science,Guangdong University of Petrochemical Technology,Maoming 525000,China)
The basic principle and the significance of variance analysismethod are discussed.Variance analysis is defined as that total variance,which is first decomposed into each variance component.Then,analysis,judgment,and appropriate conclusion are made through the use of significance testmethod.Double factor variance analysismethod is introduced and explained Through the examples,and questions raised by students are answered,such as how to judge the plurality in testing the components of a sample using several differentmethods by different investors and why every kind of analyticalmethod are repeated several times,and how to judge if there is significant difference in results between different analysismethods and investors.
variance;variance analysis;double factors;no repeat;judgment
O212.1
A
10.3969/j.issn.1672-4550.2014.05.012
2013-05-31;修改日期:2013-07-02
杨小勇(1959-),男,大学本科,高级实验师,主要从事物理化学实验教学工作。
