大位移井套管轴向力对套管挠度的影响

孙铭新，张大千，步玉环，孙 旺

（1．胜利石油管理局钻井工艺研究院，山东 东营 257017；2．中国石油大学石油工程学院，山东 青岛 266580）

大位移井套管轴向力对套管挠度的影响

孙铭新1，张大千2，步玉环2，孙 旺2

（1．胜利石油管理局钻井工艺研究院，山东 东营 257017；2．中国石油大学石油工程学院，山东 青岛 266580）

大位移井套管在重力效应作用下使套管偏心并产生挠曲变形，大幅降低水泥浆的顶替效率，影响固井质量，现场一般采用安装扶正器的方法改善套管的偏心；而两扶正器间的套管在井斜的影响下，套管自重会在轴向上产生一定的分力，井斜角越大其分力越大，对套管的挠度产生的影响也越大。采用纵横弯曲梁理论建立了套管挠度计算模型，并定义了挠度影响因子的概念，在此基础上研究了挠度影响因子随轴向力的变化规律及轴向力对套管挠度的影响。研究结果表明：在轴向力对套管挠度的影响方面存在1个临界力，小于临界力时轴向力对套管挠度的影响可以忽略，大于临界力时轴向力对套管挠度的影响显著；临界力的大小与扶正器间距、套管的弹性模量以及套管截面的轴惯性矩的相关性可以忽略。研究结果间接证明：大位移井中下套管作业时，现场利用套管的自重使套管下入预定深度的正确性，可以有效地减小两扶正器间套管的挠曲变形，并对大位移井扶正器的优化设计具有一定的指导意义。

大位移井；轴向力；影响因子；挠度；扶正器间距

大位移井的套管偏心一直是影响固井质量的难题，为了提高固井质量，现场一般采用安装扶正器的方法来改善套管的偏心［1］，而扶正器是隔段安装的，相邻两扶正器之间的套管由于重力作用将会产生挠曲变形，在挠度大的位置会产生水泥浆窜槽而影响固井质量。因此，合理分析套管的挠曲变形显得尤为重要，很多学者提出了计算相邻两扶正器间套管最大挠度的方法，用以确定扶正器的安放间距［2-4］；利用瑞利-里兹能量法导出了挠度计算公式［5］等，但是对套管轴向力等因素对套管挠度的影响规律研究较少。套管在井底的受力十分复杂，重力是影响套管挠曲变形的关键因素之一［6］，套管轴向上的受力对套管挠度的变化［7］及套管偏心的影响也非常关键。为此，详细分析轴向力对套管挠度的影响规律，对于确定扶正器的合理安放间距、提高固井质量具有一定的指导意义。

本文利用纵横弯曲梁理论［8］，建立两相邻扶正器间套管挠度计算模型，并进行受轴向拉力和轴向压力2种情况下的套管挠度变化规律分析，从而得出轴向力对套管挠度的影响规律，为合理确定扶正器的安放间距提供一定的依据。

1 计算模型

合理的扶正器安放间距是提高固井质量的关键，计算扶正器安放间距的核心是准确地计算相邻两扶正器间套管的挠度。本文根据纵横弯曲梁理论，将扶正器假设为铰支座，同时考虑轴向载荷、径向载荷和扶正器处弯矩对套管变形的影响，建立大位移井段相邻两扶正器间套管（1跨套管）的变形模型，如图1（轴向拉力）。

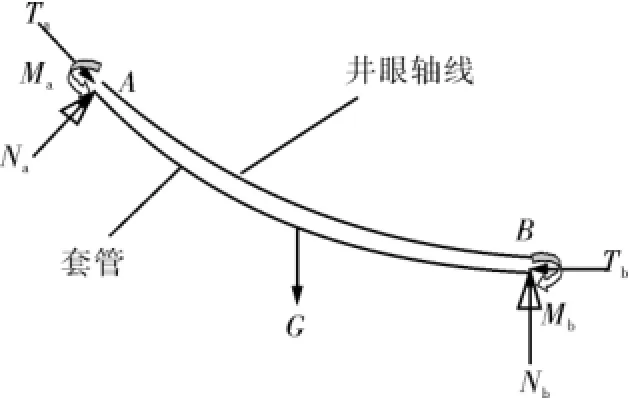
图1 套管变形模型

利用纵横弯曲梁理论建立套管变形模型，并根据新叠加原理［8］，首先计算径向力、上扶正器处弯矩、下扶正器处弯矩分别和轴向力共同作用时对套管挠度的影响，然后进行线性叠加，即可得出最大挠度的计算模型。

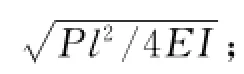
式（1）～（2）可合并为通用式，即

式中：X（u）、Y（u）为轴向力对套管挠度的影响系数。

由于轴向拉力和轴向压力对挠度的影响规律不同，前人只将轴向压力影响下的系数定义为放大因子［8］，笔者将它们统一命名为轴向力对套管挠度的影响因子，简称轴向力影响因子。

将式（1）～（3）进行对比，当轴向力为拉力时，轴向力影响因子为

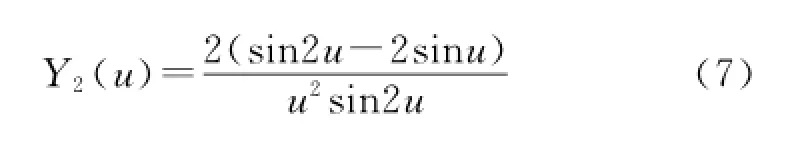
2 轴向力影响因子对套管挠度的影响

由于大位移井存在大斜度井段，在大斜度井段套管自重将在径向和轴向上产生分力，同时扶正器存在摩阻力，综合分析轴向力对套管挠度的影响规律对于下套管作业具有重要的指导意义。

1） 当P→0时，u→0。

对X1（u）、Y1（u）、X2（u）、Y2（u）取极限，当从轴向拉力一侧趋近于零时，有

式（12）即为套管不受轴向力时的最大挠度计算公式，它与利用纵横弯曲梁理论推导出的无轴向力时的套管最大挠度计算公式是一致的［8］。

2） 当P≠0时，u≠0。

由于当P→0时，从轴向拉力一侧来看，当P≠0时，X1（u）始终是小于1的，Y1（u）始终是大于－1的，由此可知轴向拉力会降低套管的最大挠度；同理从轴向压力一侧来看，X2（u）始终大于1，Y2（u）始终小于－1。换言之，轴向压力会增加套管的挠度。

研究表明：轴向拉力会降低套管的挠度，套管挠度越小，扶正器的许可安装间距就越大，安放数目就越少，这样既能保证套管的合理居中度，又能保证套管的顺利下入。因此，充分利用套管自重产生的轴向拉力，尽量使套管处于受拉状态有利于套管的顺利下入。这就要求应保证井壁良好的光滑性，选用适当的扶正器类型，且合理布置扶正器安放间距，以降低下套管过程中的摩擦阻力。

3 轴向力对影响因子的影响

通过以上分析可知，轴向力通过改变影响因子间接影响套管挠度的大小；同时由式（3）可以看出，影响因子受到多种因素的影响。根据控制变量法，为了更直观地分析影响因子随轴向力这个单一因素的变化规律，分析轴向力对套管挠度的影响规律，首先要分析轴向力对影响因子的影响，从而得出轴向力对套管挠度的影响规律，为大位移井固井作业中扶正器的安放位置提供理论指导。

根据控制变量法，取l＝10 m，E＝2．06×1011Pa，I＝1．916×10－5m4，当P（拉力和压力）从0增加到100 k N时，影响因子的变化规律如图2所示。

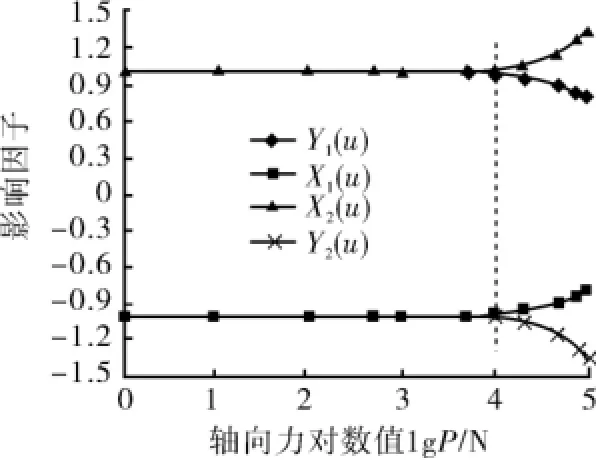
图2 影响因子变化规律

图2中：横坐标是以10为基底的对数刻度坐标；X1（u）、Y1（u）代表轴向x为拉力时影响因子的变化规律；X2（u）、Y2（u）代表轴向x为压力时影响因子的变化规律。由图2可以看出：以轴向力为10 k N为分界点，轴向力小于10 k N时，影响因子变化很小；轴向力大于10 k N时，影响因子的变化非常显著，表明此时轴向力对影响因子的影响很大。

4 分界点处临界力的变化规律

为了分析分界点处临界力的变化规律，笔者又分别改变了扶正器间距、弹性模量和套管截面的轴惯性矩的值，分别将l＝10 m，E＝2．06×1011Pa，I＝1．916×10－5m4改变为l＝12 mm，E＝1．9× 1011Pa，I＝8．17×10－6m4得出轴向力对影响因子的影响规律，如图3所示。图3中：横坐标是以10为基底的对数刻度坐标；曲线1～4是改变扶正器间距后的影响因子变化曲线；曲线5～8是改变弹性模量后的影响因子变化曲线；曲线9～12是改变惯性矩后的影响因子变化曲线。其中：曲线1、2、5、6、9、10是轴向拉力影响下的曲线；曲线3、4、7、8、11、12是轴向压力影响下的曲线。

由图3可以看出：分界点处临界力的大小约为10 k N，说明改变扶正器间距、弹性模量和惯性矩对分界点处临界力的影响不大。

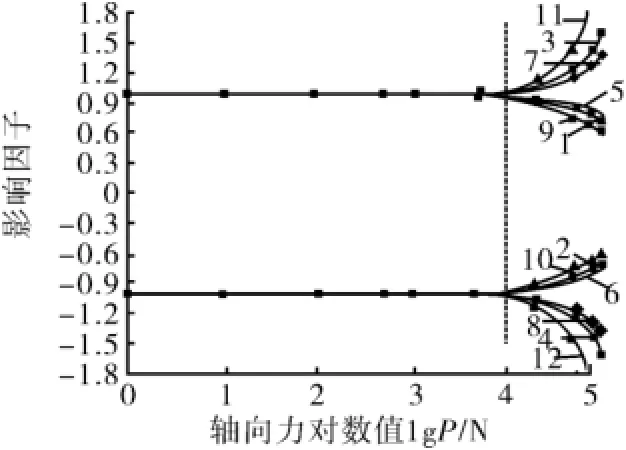
图3 影响因子上分界点对比

5 轴向力对套管挠度的影响

5．1 影响规律

同理，根据控制变量法，取l＝10 m，E＝2．06× 1011Pa，I＝1．916×10－5m4，P的取值同上，θ＝60°，Ma＝Mb＝ql2／12，q＝400 N／m，则轴向力对套管挠度的影响规律如图4。

图4 套管挠度与轴向力关系曲线

图4中：横坐标是以10为基底的对数刻度坐标。由图4可以看出：套管挠度随轴向力变化的分界点处临界力基本也是10 k N，分界点之前，轴向力对挠度基本没有影响，可以忽略；分界点之后，轴向力对挠度的影响较显著。同样具有轴向拉力对套管挠度的增加表现为减弱作用、轴向压力对套管挠度的增加表现为增强作用的特点。为此，在下套管作业时，尽量使套管保持受轴向拉力状态，可以有效减小套管两扶正器间的挠曲变形，对套管的安全下入和节约成本有重要的现实意义。

5．2 临界力

为了分析轴向力影响套管挠度的分界点处临界力的变化规律，笔者又分别改变了扶正器间距、弹性模量和套管截面的轴惯性矩，分别取l＝12 m，E＝1．9×1011Pa，I＝8．17×10－6m4，得出轴向力对套管挠度的影响规律，如图5所示。

图5中：横坐标是以10为基底的对数刻度坐标；曲线1、2是改变扶正器间距后轴向拉力和压力影响下的挠度曲线；曲线3、4是改变弹性模量后轴向拉力和压力影响下的挠度曲线；曲线5、6是改变惯性矩后轴向拉力和压力影响下的挠度曲线。由图5可以看出：分界点处临界力约为10 k N，说明扶正器间距、套管的弹性模量以及惯性矩对临界力大小的影响不大。

图5 套管挠度上分界点对比

6 结论

1） 采用纵横弯曲梁理论建立了套管挠度计算模型，并将轴向力对套管挠度的影响系数定义为轴向力影响因子。在此基础上分析了轴向力影响因子随轴向力的变化规律，轴向力影响因子随轴向拉力的增大而减小，随轴向压力的增大而增大。

2） 通过分析不同扶正器间距、弹性模量和套管截面的轴惯性矩对套管挠度的分析得出，轴向力对套管挠度的影响存在一个分界点，分界点处临界力约为10 k N，临界力的大小与扶正器间距、套管的弹性模量以及惯性矩的相关性较小；临界力之前轴向力对套管挠度的影响可以忽略，临界力之后影响比较显著。

3） 通过轴向力影响因子及临界力分析表明：在下套管作业时，尽量保证套管处于受轴向拉力的状态，可以有效地减小套管两扶正器间的挠曲变形，对套管的安全下入和节约成本有重要的现实意义。

［1］孙莉，黄晓川，向兴华．国内水平井固井技术及发展［J］．钻采工艺，2005，28（5）：23-26，30．

［2］付建红，黄贵生，杨志彬，等．水平井套管扶正器合理安放位置计算［J］．西南石油大学学报：自然科学版，2008，30（6）：89-91，172．

［3］蔡长立．套管扶正器安装间距计算与应用［J］．石油钻探技术，1996，24（1）：37-39．

［4］谭树人．大斜度井、水平井套管扶正器最佳间距计算［J］．中国海上油气（工程），1993，5（4）：40-46．

［5］吴疆．套管扶正器的正确安放间距研究［J］．石油学报，1989，10（3）：86-96．

［6］王永岗，包力成．弹性梁大挠度问题的纵横弯曲法［J］．甘肃工业大学学报，1994，20（2）：59-63．

［7］朱炳坤．弯曲井段中套管柱挠曲变形的分析计算［J］．石油矿场机械，2007，36（7）：50-52．

［8］白家祉，苏义脑．井斜控制理论与实践［M］．北京：石油工业出版社，1990．

Effect of Axial Force on Casing Deflection in Extended-Reach Well

SUN Ming-xin1，ZHANG Da-qian2，BU Yu-huan2，SUN Wang2
（1．Drilling Technology Research Institute，Shengli Petroleum Administration Bureau，Dongying 257017，China；2．College of Petroleum Engineering，China University of Petroleum，Qingdao 266580，China）

Because of the gravitational effect，the casing of extended-reach well will engender eccentric and bending deformation，which will greatly reduce the cement slurry displacement efficiency and influence cementing quality．Centralizers are usually used to improve casing eccentricity on site．Under the influence of well deviation on casing between two adjacent centralizers，the casing dead weight will produce a certain component force in the axial direction，and the greater of the well deviation，the greater of the load component force，and the greater of the influence on casing bending deflection．Based on the vertical and horizontal bending beam theory，the casing deflection calculation model is established，deflection impact factor is defined，and the relationship between axial force and the deflection impact factor are studied and the casing deflection well as．It is shown that there is a critical force that when the axial force is greater than it，the impact of axial force on the deflection can be ignored，on the contrary，the influence of the axial force on the casing deflection is remarkable．And the relativity between critical force and centralizer spacing，theYoung′s modulus，the moment of inertia can be ignored．It shows that，using the dead weight of the casing to run casing can effectively reduce the casing bending deformation between two adjacent centralizers，and it has a guiding significance to the optimization design of centralizer spacing in extended-reach well．

extended-reach well；axial force；impact factor；deflection；centralizer spacing

TE931．2

A

1001-3482（2014）01-0007-04

2013-07-23

国家高技术研究发展计划（863计划）（2012 AA091501）；中国石油大学（华东）研究生创新工程资助项目（CX2013013）

孙铭新（1966-），男，山东单县人，高级工程师，主要从事科研及技术管理工作，E-mail：Sunmingxin162．slyt＠sinopec．com。