15Cr Mo实体膨胀管最优锥角有限元分析

姚 津，何继宁，任钦贵，宋开红

（河北工业大学，天津 300130）

15Cr Mo实体膨胀管最优锥角有限元分析

姚 津，何继宁，任钦贵，宋开红

（河北工业大学，天津 300130）

利用有限元分析软件，根据弹塑性有限元接触问题的相关理论建立了可膨胀管膨胀过程的力学模型。对壁厚6 mm的ø108 mm管进行膨胀过程的计算机模拟，着重研究在不同膨胀率下，膨胀锥角与锥体完成胀管所需的液压力的变化关系；确定不同膨胀率下所需的液压力最小的锥角值，即获得最优的锥角；研究了最优锥角下膨胀管的力学性能，通过参数优化设置，为现场应用提供理论依据。

膨胀锥锥角；膨胀液压力；数值模拟；最优锥角

随着国民经济飞速发展，中国石油需求量不断增长，但目前国内钻井完井周期长，采油成本较高，采用膨胀管完井技术不成熟，缺少理论指导。本文以15Cr Mo实体管为研究对象，确定了不同膨胀率下所需液压力最小的锥角值，并对经典的计算公式作了修正。

1 膨胀管技术

套管的膨胀过程涉及大塑性变形、膨胀锥和膨胀管接触位置的不断变化和管体径向尺寸的变化，是一种复杂的物理、几何非线性问题，且边界条件很复杂，采用理论分析虽然能够对膨胀管技术提供一定的指导［1］，但传统的解析方法还是很难求得其精确解。基于非线性连续介质力学原理的有限元分析方法的飞速发展，为解决塑性大变形等非线性问题提供了有效的方法［2］。这种力学有限元分析比只考虑接触问题更能直接反映膨胀作业的过程，因此，利用有限元仿真模拟技术分析可膨胀管的弹塑性变形问题是目前最理想的方法。

目前，有限元仿真模拟技术在国内石油天然气工业中已经有了一定的科研成果和实际应用。在膨胀管方面，已经用有限元分析方法分析了螺纹连接技术［3］、影响膨胀力的因素［4］以及膨胀过程中摩擦和轴向位移的关系［5］。此外，有限元仿真技术在海洋钻井方面也有一些初步研究［6-8］。

虽然有限元模拟仿真技术在膨胀管问题中已经取得了一些进展，但对某一材料在同一锥角下不同膨胀率的膨胀以及同一膨胀率下不同锥角下膨胀力大小等问题，还没有系统的理论依据和结论。而不同膨胀率下不同膨胀锥角对膨胀过程影响较大，为保证膨胀管能可靠工作，除必须保证管有足够的强度刚度外还必须保证膨胀力尽量地小。因此，本文在合理的锥角范围内对膨胀管的不同膨胀率情况进行ANSYS模拟，寻找出膨胀实体管的最优锥角和最优膨胀率，为现场应用提供理论依据。

膨胀工艺中用液压给膨胀锥提供压力，膨胀锥与套管作用实现胀管目的。但实际的液压力选取对整个膨胀工艺和膨胀后管的性能有很大影响。液压力（膨胀力）过大，则膨胀过程速度太快，导致胀后管的抗拉、抗压强度太低不能使用；液压力太小则造成膨胀过程太慢，力学性能也不理想。膨胀管和套管的接触模型如图1所示。

图1 膨胀接触模型

不同膨胀率下，不同膨胀锥角对膨胀过程影响较大，综合上述膨胀过程，由经典的塑性力学可知其膨胀力为

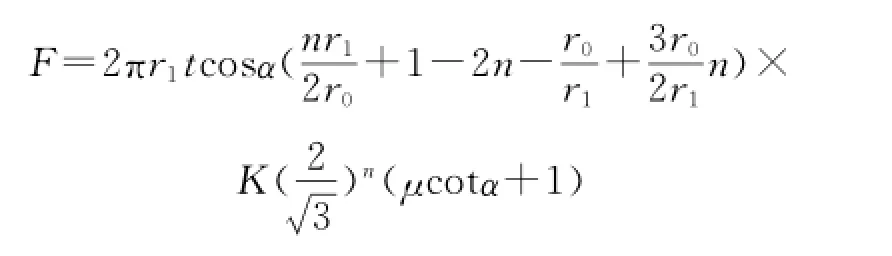
式中：r0为膨胀前管半径；r1为膨胀后管半径；n为硬化指数；μ为摩擦因数；k为材料系数。

通过实际膨胀试验，上述公式不能真实反映膨胀力大小，存在一定误差，对胀后管体的力学性能没有量化的数学表达。基于以上膨胀过程，本文给予了研究分析。

膨胀管膨胀是一个相对运动过程，在管体膨胀时，膨胀锥和膨胀管表面之间不发生相互渗透，在锥膨胀管的过程中锥的推进速度一般为9～15 m／min［1］，忽略膨胀过程中的热效应。根据金属塑性理论，大多数材料都有一定程度的率相关性，但此处膨胀锥速度较均匀，可认为是与率无关的。由固体力学的相关理论可知：大应变的塑性分析一般采用真实的应力、应变数据，并且根据膨胀管的实施技术可以把膨胀管工艺近似看作膨胀锥和膨胀管的接触非线性大变形问题。根据屈服准则和强化准则，非线性大变形问题用等向强化准则来模拟计算。由于膨胀锥材料的强度远大于膨胀套管，更应关心管体的变形情况，故本文将其作为三维刚柔接触问题来研究，即假设可膨胀管为柔性体，膨胀工具为刚性体。

本次ANSYS模拟所使用的管暂时没有考虑套管的初始几何缺陷（椭圆度、壁厚不均度等），即假设这些套管材质均匀，壁厚均匀，管体内外径的圆度和同心度很高，即假设这些套管为理想的同心管。膨胀管规格：膨胀前管体外径108 mm、壁厚6 mm、长度500 mm；膨胀锥定径区和润滑区的长度为50 mm。模拟的膨胀过程为：膨胀管的上端固定，下端可以自由移动（即自上而下式膨胀工艺）。

2 有限元分析

利用ANSYS12．1下的Workbench全新平台进行模拟，步骤如下。

2．1 建立有限元模型

所需膨胀套管的结构具有对称性，且大变形非线性有限元计算过程消耗的资源大、运算时间长，建模时考虑到减小问题规模，故分析时取整个模型的1／4来进行仿真计算。

首先调入用UG创建的三维造型X_T文件，随后划分网格生成有限元模型。其中实体管为15Cr Mo，其弹性模量212 GPa，泊松比0．3，屈服强度365 MPa，切线模量79 GPa。根据本文的研究内容对管体和锥体进行Element sizing值分别为5和7的网格划分。划分好的网格模型如图2所示。

图2 有限元模型

2．2 加载并求解

在1／4模型的分割面上对模型施加如图3所示的x轴向、y轴向和z轴端面的约束。

图3 实体管加载

完成上述步骤后，求解。在Solution添加Deformation Total和Stress Equivalent结果，完成后再点击solve进行进一步求解。

3 描述模拟结果

3．1 膨胀力和膨胀锥角间的关系

图4为管体在膨胀10%～30%时不同锥角下液压力的ANSYS模拟数据。由图4可知：在锥角由7°～21°变化的过程中，其膨胀力呈一定规律变化；液压力随着膨胀锥角度由7°变为21°，呈现先减小后增大即“类抛物线”规律，某一角度处膨胀力最小；膨胀率为10%时，在9°时达到最小值，最小液压力为26．913 MPa。

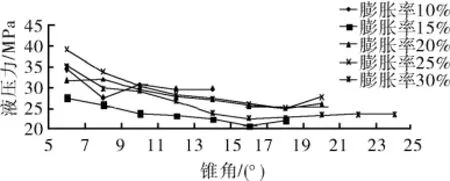
图4 不同锥角下膨胀率与液压的关系

3．2 膨胀锥角与膨胀变形率间的关系

管体在锥角一定时，膨胀率在10%～30%变化时ANSYS的模拟数据如图5，可以看出：膨胀率由10%～30%变化的过程中，膨胀液压同样表现出先减小后增大的趋势。可以看出在膨胀率为15%时膨胀力在各固定锥角都达到了最小值。如膨胀率15%、锥角为7°时，所需最小液压力为26．922 MPa。

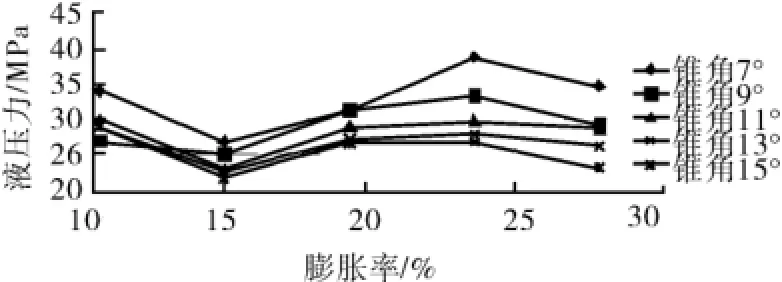
图5 不同膨胀率下锥角与液压的关系

4 有限元结果分析

膨胀管膨胀时，膨胀锥的外表面和实体管的内表面是相互接触的，而且随着膨胀过程的进行将不断产生新的接触面，膨胀锥和膨胀管之间的接触为摩擦型。在Mechanical中摩擦采用库伦（Coulomb）模型，在模拟过程中假设摩擦只发生在锥与管的接触界面，且摩擦因数在膨胀过程中始终保持不变。因此，膨胀力的大小和摩擦因数、接触面积S有关。由于膨胀锥体和管之间还存在金属的变形挤压，故和金属剪切力的大小也有一定关系。

4．1 摩擦影响

关于摩擦因数μ的影响，ANSYS程序主要提供了2种算法，即常摩擦因子法和常摩擦因数法，计算时可通过一定的参数设定来选择所用的摩擦算法。由于在膨胀过程中锥和管的材料已知，在考虑相同润滑时，它们之间的摩擦因数基本不变，故本文采用常摩擦因数法来进行膨胀管的仿真模拟。

4.2 剪切力τ影响

上述不同角度的膨胀锥和管的接触面积都不相同。膨胀锥可分导正、膨胀、保径3部分。其中不同锥角的导正部分和保径部分受力都相同，只有膨胀部分不同。

锥角17°时的膨胀力和表面积的数据如表1。当不同膨胀率同一锥角时其接触面积发生改变，但接触面积的相对增长率和膨胀力的大小变化并不成正比关系，且表面积的变化率比膨胀力的变化率大得多，这说明此时影响膨胀力的主要因素不是接触面积，而是其在金属发生塑性变形时的剪切力起主要影响因素。

表1 锥角17°时不同膨胀率的接触面积

膨胀过程从工艺上讲分为膨胀锥初始进入、稳定膨胀和膨胀结束3个阶段。在膨胀锥初始进入阶段膨胀力不断增大，锥体完全进入和稳定膨胀阶段膨胀力趋于稳定值。在锥体初始进入时膨胀力不断增大，主要是由于剪切量的不断增大导致剪切力不断增大，当达到剪切极限时发生金属的流动，形成永久塑性变形达到膨胀目的。此时剪切速度也对膨胀的剪切力有一定的影响。

在膨胀管与锥体接触过程中，2个接触面在开始相互滑动之前，它们的界面上会有达到某一大小的剪应力。这种状态称为粘合状态（Stick）。定义一个等效剪应力τ，在某一法向压应力p作用下剪应力达到τ＝μP＋C时表面开始滑动，（其中μP为摩擦因数，C为粘聚力）。膨胀管与膨胀锥相互接触的过程中剪应力超过此值后，2个表面之间将开始相互滑动。根据塑性理论中2个金属接触表面发生相互剪切时，可以认为是纯剪切力作用下的金属形变，与之相互剪切的剪切面大小无关，只和金属的拉伸曲线上塑性变形阶段有关。即膨胀管材料随着膨胀力的增大达到屈服点，膨胀管材料开始出现塑性变形，金属开始剪切，发生位移达到膨胀目的。而不同的膨胀率由于膨胀锥的最优角不同，其接触面积之间的剪切部分也不同，包括剪切部分空间的大小、剪切的速率和其他接触力的影响。所以剪切力在膨胀率相同时其大小基本相同，在同一锥角不同膨胀率时虽其接触部分空间不同，但其金属之间的相对滑动主要由金属的材料属性决定，即剪切力大小决定。

根据以上理论可知：锥角一定时，剪切力在膨胀过程中是影响膨胀力变化的主要影响因素；正如图5所示膨胀率为15%时液压力最小，即说明15Cr Mo在锥角一定时膨胀率为15%剪切力τ最小，膨胀率15%为最优解。

4．3 接触面积影响

膨胀率15%不同锥角的表面积及变化如表2，由表2数据可知：在膨胀率相同，锥角不同时，其剪切力影响因素较小，摩擦接触面积影响较大，随着接触面积的增大，其膨胀力也基本成正比增大，在膨胀率15%时，锥角为17°时膨胀力最小为最优解。

表2 膨胀率15%时不同锥角的表面积及变化

膨胀率一定时，随着锥角的减小接触面积增大，在剪切力影响不大的前提下，其膨胀力也随着接触面积增大而趋于线性正比增大，根据ANSYS接触理论，膨胀锥和膨胀管为强制接触协调，服从Coulomb定律：Ftangential≤μ·Fnormal，其中Fnormal为正压力，与接触面积成正比；Ftangential为切向摩擦力。上述结论进一步证明了不同膨胀率时都存在一个最优膨胀锥角。

4．4 胀后管体性能比较

用Ansys模拟得到的最优膨胀锥角经过膨胀试验和未利用仿真数据胀后管的力学性能做比较。其中，Ansys模拟抗压极限载荷如图6所示。经过Ansys模拟和实际膨胀得出最优解的力学性能。

图6 套管承受极限抗压载荷

利用Ansys仿真数据胀后管的力学性能如表3～4，与实际的相比，胀后管的抗拉、抗压强度及抗挤毁都有很大提高，相关的模拟数值能反映胀后管的真实性能，为膨胀管的实际应用提供了理论参考。

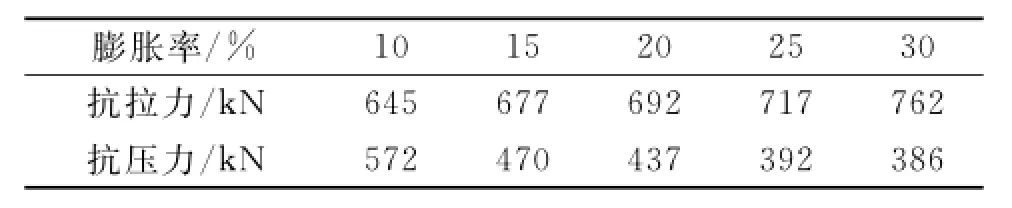
表3 抗拉、抗压极限载荷

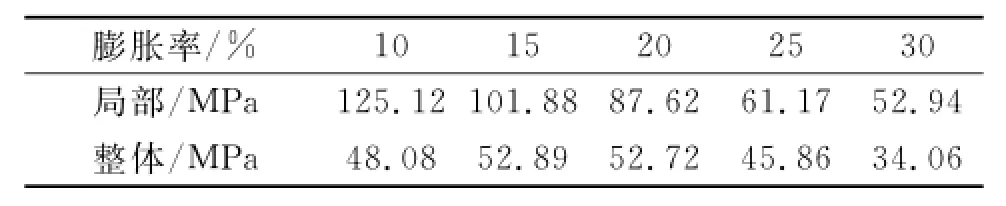
表4 抗挤毁强度

5 经典公式修正

通过Ansys仿真数据与经典计算公式结果相比较，仿真的膨胀力较经典的结果都大一个值，在此把它定义为修正值δ，通过15Cr Mo膨胀10%～30%的数据可以得出修正值，范围为0．826～1．768 MPa。δ根据不同的材料而变化，其值的大小可以根据仿真得出，则15Cr Mo的膨胀力公式可以修正为

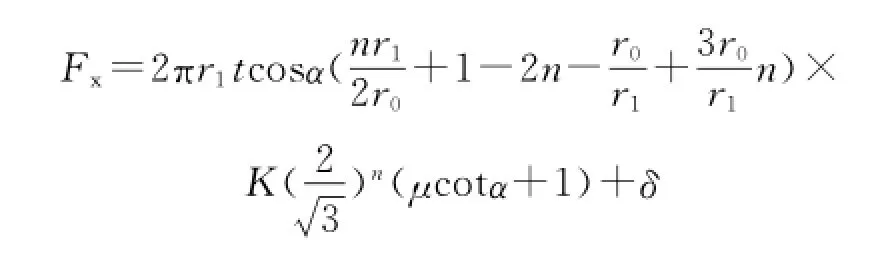
6 结论

1） 尽管在不同的锥角下得到的液压驱动力差别较大，但是在取得驱动力最小峰值的锥角周围，驱动力随锥角的变化较小，一旦远离最佳锥角，驱动力随锥角的变化则较大。

2） 通过研究不同膨胀率下的膨胀锥角与锥体完成膨胀所需的液压力的变化关系，确定了不同膨胀率下所需的液压力最小锥角值，即获得最优的锥角。

3） 锥角一定时，剪切力在膨胀过程中影响膨胀力的变化占主要影响因素。仿真数据说明：15Cr Mo在锥角一定、膨胀率为15%时剪切力最小，为最优解。

4） 膨胀力的变化符合经典的塑性理论的变化规律，其较真实的模拟数据为膨胀工艺提供了技术参数，对膨胀工艺参数的确定提供了有效理论依据，为膨胀管技术的实际应用奠定了理论基础。

［1］秦国明，何东升，张丽萍，等．基于ANSYS／LS-DYNA的实体膨胀管膨胀力分析［J］．石油矿场机械，2009，38（8）：9-12．

［2］付胜利，高德利，易先中，等．实体可膨胀管变形力与膨胀工具模角关系研究［J］．石油机械，2006，34（1）：25-27．

［3］肖凯文，李黔，尹虎，等．一种新型膨胀管螺纹的连接可靠性分析及试验［J］．石油天然气学报，2012，34（6）：112-114．

［4］梁坤，练章华，任荣坤，等．实体膨胀管膨胀力影响因素数值模拟［J］．石油矿场机械，2010，39（12）：1-4．

［5］秦永和，付胜利，高德利．实体膨胀管膨胀后轴向位移有限元数值模拟［J］．石油钻采工艺，2006，28（5）：1-3．

［6］郑晓晶，周国强，郭奕珊．海洋石油钻机井架动力特性分析［J］．大庆石油学研学报，2005，29（3）：53-54．

［7］秦太验，柳春图，段梦兰，等．具有裂纹损失桩腿的海洋石油平台有限元分析［J］．海洋工程，2000，18（3）：15-19．

［8］刘金梅，周国强，韩国有，等．波浪作用下海洋石油井架模态参数识别与承载力评价［J］．海洋工程，2009，27（1）：22-27．

Finite Element Analysis of Optimal Angle of Entity Expansion Pipe of 15Cr Mo

YAO Jin，HE Ji-ning，REN Qin-gui，SONG Kai-hong
（Hebei University of Technology，Tianjin 300130，China）

By utilizing the finite element ansys software and basing on the related theory of elasticplastic finite element contact problem，the mechanics model of the expansion pipe in an expanding process was constructed．By simulating the expansion process of the 108 pip whose wall thickness is 6 mm，the relationship between the fluid pressure was studied，which is needed to complete the expansion and the different expansion ratio and expansive cone angle．It confirmed the best angle in different expanding inflation and researched mechanical properties of expansion pipe at the optimal angle．And it will provide an important guide to the field application．

expandable tool coning；expansion fluid pressure；numerical simulation；the optimal angle

TE931．2

A

1001-3482（2014）01-0025-05

2013-07-05

姚 津（1987-），女，河北石家庄人，硕士研究生，主要从事石油膨胀管研究，E-mail：youyouguoguo_1987＠126．com。