基于矩阵特征值分析的模糊聚类有效性指标

岳士弘，黄 媞，王鹏龙

(天津大学电气与自动化工程学院，天津 300072)

基于矩阵特征值分析的模糊聚类有效性指标

岳士弘，黄 媞，王鹏龙

(天津大学电气与自动化工程学院，天津 300072)

许多有效性指标已经被提出量化地估计和评价模糊聚类算法对于给定数据集的划分结果．但是由于不合理的结构和极大的时间耗费，迄今这些有效性指标几乎都无法满足应用的一般性需求．为此，提出一个基于Gerschgorin 圆盘定律估计的聚类有效性指标来估计模糊聚类的类数．先由模糊聚类划分的结果得到一个相关性矩阵，接着求出该矩阵的所有特征值和特征向量，然后基于经典 Gerschgorin 圆盘定律估计最优的类数．为了检验提出的指标在模糊聚类中的有效性，把模糊聚类算法应用到带有不同特征的3个人工数据集和3个真实的数据集，并比较提出的指标和 2个最常用的模糊聚类有效性指标．实验结果证明了所提出的有效性指标能够发现被聚类数据集的固有结构，从而得出更加准确的类数．

有效性指标；Gerschgorin圆盘；模糊聚类；特征值

聚类分析是一类无监督式的学习技术，目的是把一个模式集中，具有类似特征的模式划分到相同类而把不同特征的模式划分到不同类[1]．聚类分析的一个关键任务是量化地评价聚类结果，尤其是确定一个最优的类数或划分结构．通常，这种评价由一个或一组聚类有效性指标来完成[2-3]．

大多数聚类有效性指标都是基于 2个最常用的聚类算法设计：硬聚类的 HCM(hard c-means)算法[4]和模糊聚类的FCM(fuzzy c-means)算法[5]．因此有效性指标可以进一步划分为2大类：硬聚类指标是用来评价和估计硬聚类算法的聚类结果；模糊聚类指标是使用模糊隶属度确定模式对于类的归属性．本文聚焦在模糊聚类有效性指标的研究．

迄今为止，研究者已经提出大量聚类有效性指标．2个最常用的模糊聚类指标是 Bezdek[5]提出的信息熵指标以及 Xie等[6]提出的分离性指标．其次，研究者已经提出充分考虑数据集结构的聚类有效性指标，如 Kim 等[7-8]在分析已有有效性指标与数据集的关系后提出一系列新的有效性指标．Maulik等[9-11]在提出一个既适合硬聚类又适合模糊聚类的指标后，又研究了该指标相对于不同数据结构的变化形式．最近，Yue等[12]提出一个基于网格距离度量不同类之间分离性的有效性指标等，该指标可以度量包含任意形状类的数据集的结构．但这些指标都是通过一种迭代的 trial-and-error过程[13]来确定数据集最佳聚类数，即这些指标都必须使聚类算法遍历所有可能的类数实施聚类，从而确定哪一个聚类结果是最优的．由于聚类算法必须被反复履行，因此是极其耗费时间的，这直接导致已有的有效性指标无法应用在大多数工程中．陈黎飞等[14]最近提出一个基于层次划分的方法试图解决这个问题，但这种方法并没有根本改变上述问题，同时又产生层次聚类算法参数过度敏感的固有问题．

本文提出一个基于Gerschgorin圆盘定理[15]的有效性指标估计最优的类数．首先，使用一个充分大的类数代入 FCM算法对数据集进行模糊聚类，接着按照模糊聚类结果构造一个所有类之间的相关矩阵；在确定这个相关矩阵的 Gerschgorin圆盘后，把所有的Gerschgorin圆盘划分到具有较大特征值和较小特征值的 2个不同集合；最后，基于 Gerschgorin圆盘定理提出一个新的有效性指标．该指标最少只需要一次聚类就可以得到最优的类数，从根本上改变和克服了已有聚类有效性指标遍历式搜索所有可能类数所带来的低效率，而得到最优类数的正确率并不比已有的有效性指标低．为了证明新提出有效性指标的价值，本文在一组具有不同特征的数据集中，选择了3个具有代表性的模糊有效性指标进行比较分析：Bezdek[5]提出的信息熵指标，Xie等[6]提出的分离性指标，Pakhira等[10]提出的可以同时评估硬聚类和模糊聚类结果的有效性指标．实验结果证明了本文提出指标的正确性和高效率．

1 相关工作

首先说明一个应用最广泛的模糊聚类算法——模糊c-均值(fuzzy c-means，FCM)算法，以及3个有代表性的模糊聚类有效性指标——Bezdek[5]提出的信息熵指标，Xie等[6]提出的分离性指标，Pakhira等[9]提出的有效性指标，说明这些指标的可应用范围．

1.1 模糊聚类算法

许多聚类算法可以实施模糊聚类，但是这些算法都源自于Bezdek的FCM算法[5]．由于良好的可理解性和可操作性，FCM 算法仍然是当前工程界应用最普遍的聚类算法．

给定一个带有 n个目标和 c个类的模式集 X= {xi}，FCM算法的目标函数为

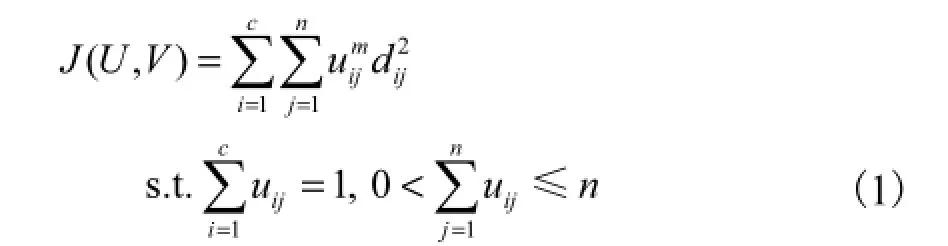
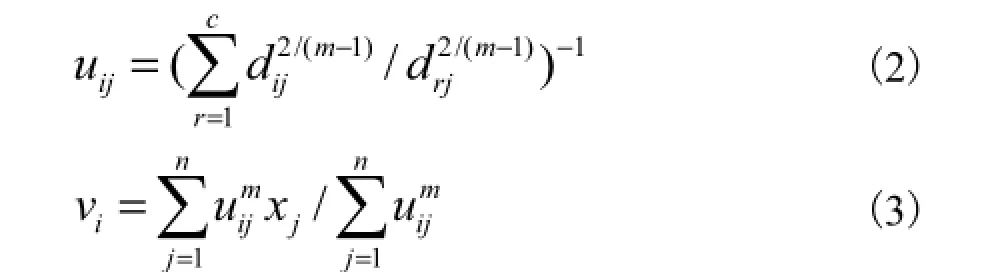
如果m=1且uij的值只取0或者1，则FCM退化为HCM算法．但是 FCM算法的聚类结果严重依赖参数c(一个预设或者使用者输入的类数)．如果c预先未知导致输入一个错误的类数，则 FCM 的聚类结果是不可信甚至是无意义的．解决这个问题的一个常用方法就是使用一个或几个聚类有效性指标[2-3]来确定一个最优的类数．

1.2 3个有代表性的模糊聚类有效性指标

1.2.1 Bezdek的信息熵指标

Bezdek提出信息熵指标表达式[5]为

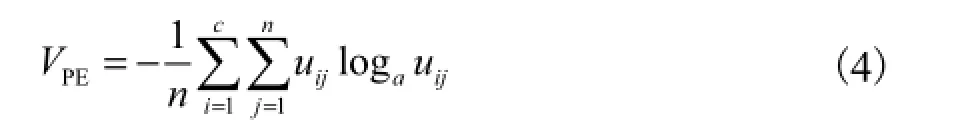
式中a为一个对数函数的底数．这个指标是一个基于信息熵的结构设计、基于模糊隶属度计算的关于类数的函数关系．让类数从 1递增到一个足够大的整数，则最优的类数通过求解VPE的最小值获得．

1.2.2 Xie等提出的分离性指标

Xie和Beni提出的基于分离性的有效性指标[6]为

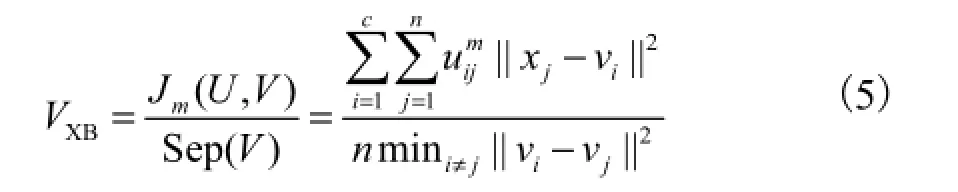
这个有效性指标实际上是通过极大化类间距而极小化类内距的形式构造，最优的类数通过极小化式(5)中的目标函数来获得．

1.2.3 Pakhira等提出的有效性指标

Pakhira等[10]提出一个能同时评价硬聚类和模糊聚类结果的有效性指标，即

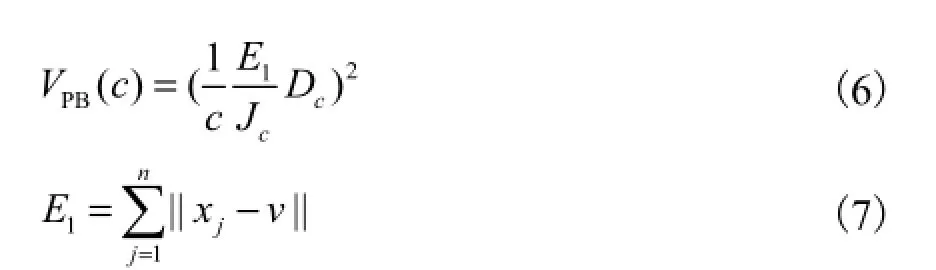
式中：v为数据集中心；Jc为FCM或HCM算法中目标函数的值；Dc为所有不同聚类原型之间的距离总和，则最优的类数通过求解VPB的最小值获得．

从上述说明可以观察到，已有的有效性指标都是通过遍历所有可能的类数进行聚类，并最终确定哪个聚类结果或类数是最优的．因此，必须不断地对数据集实施聚类，而在工程实践中这基本是不可行的．同时，如果类数的范围选择不合适，这类指标可能根本达不到任何一个最优值．例如，式(2)和式(3)所对应的指标，当类数的取值范围趋向于无穷大时，这2个指标的变化趋势趋向于单调下降[2,13]，这说明它们的结构也存在着一定的不合理性．

2 新的聚类有效性指标

首先基于FCM算法的聚类结果计算任何2个类之间的相关系数，使用所有相关系数组成一个相关矩阵；在计算相关矩阵的所有特征值之后，使用Gerschgorin圆盘定理估计正确的类数．

2.1 相关系数和相关矩阵

给定d维数据集X′={X1，X2，…，XR，…，Xn}，Xk为一个数据点，Xk=(xk1，…，xkd) ∈Rd，k=1，2，…，n，n为数据点的总数．设L为FCM算法中设定的类数，在实施 FCM聚类后得到一个对X的模糊划分，用一个模糊划分矩阵表示为

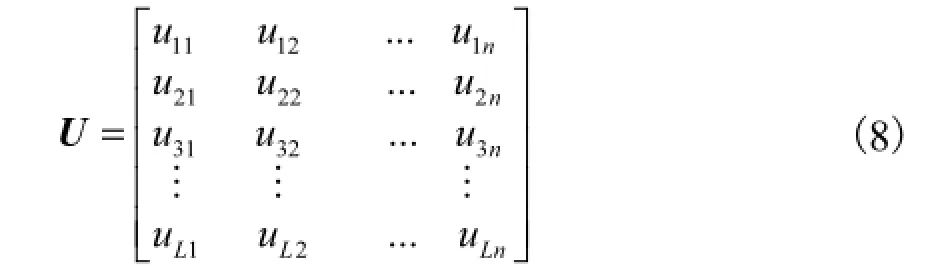
根据式(8)，定义2个统计量分别为

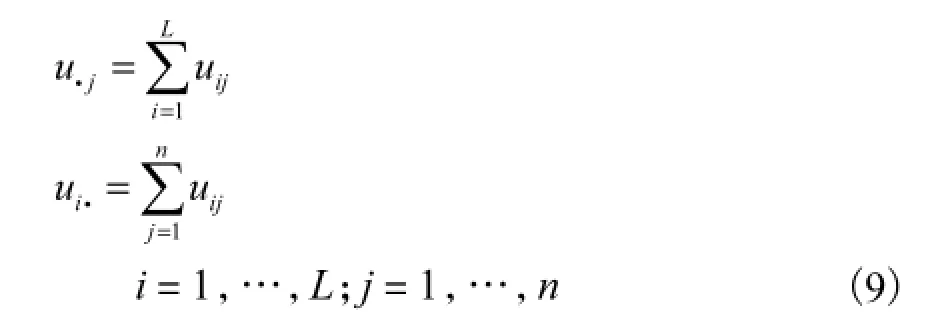
这 2个量分别表示相应点(模式)或相应类的重要度．假设某个聚类算法把数据集 X划分到 L个类C1，C2，…，CL，因此定义任意 2个类iC和jC的相关系数为

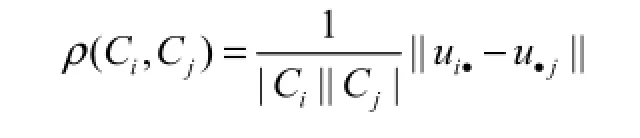
按照式(10)计算所有类之间的相关系数后，得到相关矩阵

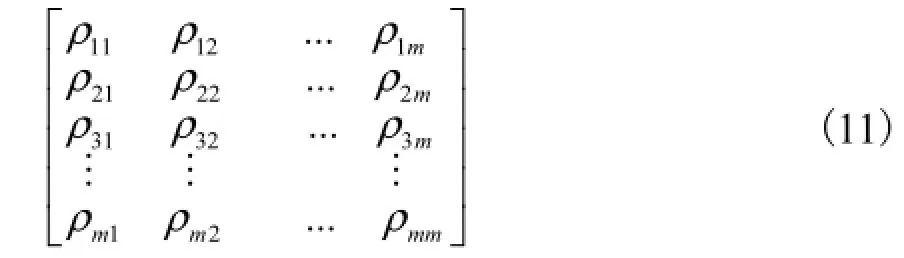
显然，式(11)所表达的相关矩阵是一个实对称的矩阵，因而必有L个实数特征根．

2.2 Gerschgorin圆盘定理和估计原则

λi( i = 1,2,… ,L)是式(11)的L个依照递减顺序排列的特征值．设A=(aij)nn×∈R ，称由不等式

在复平面上确定的区域为矩阵 A的第i个 Gerschgorin圆盘，并用iG表示，其中

称为盖氏圆盘 Gi的半径，i=1,2,…,n．

定理 1(Gerschgorin圆盘定理 1)[15].矩阵 A= (aij) ∈Rn×n的一切特征值都在它的n个盖氏圆盘的并集之内．

定理1为可视化地观察Gerschgorin圆盘分布提供了依据，更一般地有如下结论．

定理2(Gerschgorin圆盘定理2)[15].由矩阵A的所有盖氏圆盘组成的连通部分中任取一个，如果它由k个盖氏圆盘构成的，则在这个连通部分有且仅有 A的k个特征值．

定理 2说明了盖氏圆盘集的可分离性．在使用FCM 算法时，选择不同的类数可能导致聚类结果出现以下3种情况[2,12].

(1) 选择的类数比真实的类数大．这种情况下，一些原本完整的类不得不被强制分成更多的类，并且往往是样本数很少的类．

(2) 选择的类数比真实的类数小．这种情况下，一些原本分离性很好并属于不同类的点被不正确地划分到同一类，一些类的中心不得不位于样本点很稀疏的位置以使 FCM 的目标函数最小，从而极大地降低类内点之间的相似度．

(3) 选择的类数等于真实的类数．这种情况下，FCM 算法的聚类结果是最佳的，或者说被错误划分的数据点数目最少．

根据相关矩阵的定义和特征值的计算过程可知，特征根的大小反映了所划分类的类内样本的相似程度．依照Gerschgorin圆盘定理，如果实际的类数是c个，则其L个特征值出现的情况为

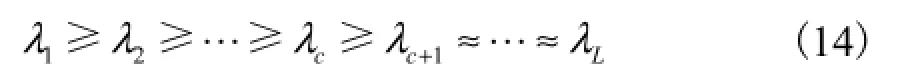
式中1cλ+到Lλ是(L c- )个相对小的特征根．因此，实际类对应的圆盘和其他类对应圆盘可以按照特征值的大小明显地分开．一般地，按照 Gerschgorin圆盘定理，本文提出指标求解最优的类数，即

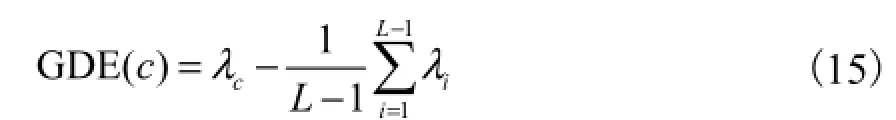
式中c为一个整数，是在闭集合[1, 1]L- 内所取的可能的类数．而式(15)的右边第 2项是所有特征值的平均．则GDE()c的类数确定法则为：当第 1个非负的GDE()c值出现时所对应的类数为最优的类数．

3 实 验

以下把本文提出的基于 Gerschgorin圆盘估计的有效性指标称为 GDE指标．同时，称 Bezdek[5]提出的信息熵指标为 VPE，Xie等[6]提出的分离性指标为VXB，Pakhira等[9]提出的有效性指标为 VPB．GDE被用于评价FCM聚类结果并与VPE、VXB和VPB的结果做比较．本文使用3个具有代表性的人工数据集和3个来自 UCI的真实数据集来测试和比较这些有效性指标的正确性，具体过程和结果描述如下．

3.1 测试的数据集

3个人工数据集都使用 Matlab工具包产生．正确的类标号可以从产生这些数据的“randn()”函数确定．这些类标号用来评价聚类结果的正确性，而不参加聚类过程．这 3个三维的人工数据集分别标记为数据集1、数据集2和数据集3，图1(a)～(c)显示了这3个数据集中数据点的分布．

数据集1包含6,000个点，这些点分布在3个类中，其中一个是包含 4,000个点的高密度的类，另外2个是分别包含1,000个点的低密度的类，这个数据集被用于模拟包含密度不均匀类的数据集(见图1(a))．数据集2包含5,000个点的类，其中5个类是分布在水平方向的非球状的类，另一个是沿着竖直方向分布的类(见图1(b))．数据集3包含6,366个点，分布在 15个类中，其中一些类带有部分交叠(见图1(c))．

另一方面，本实验选择来自UCI的3个真实数据集进行测试，具体描述如下．

(1) Iris数据集．这是一个包含150个样本并且每个样本带有4个特征的数据集．这150个样本均分在3个类中，每个类各有50个样本，其中2个类带有部分交叠而另一个类独立于这2个类．在过去的几十年中，Iris数据集是使用最频繁的用于测试聚类有效性的数据集[16-17]．

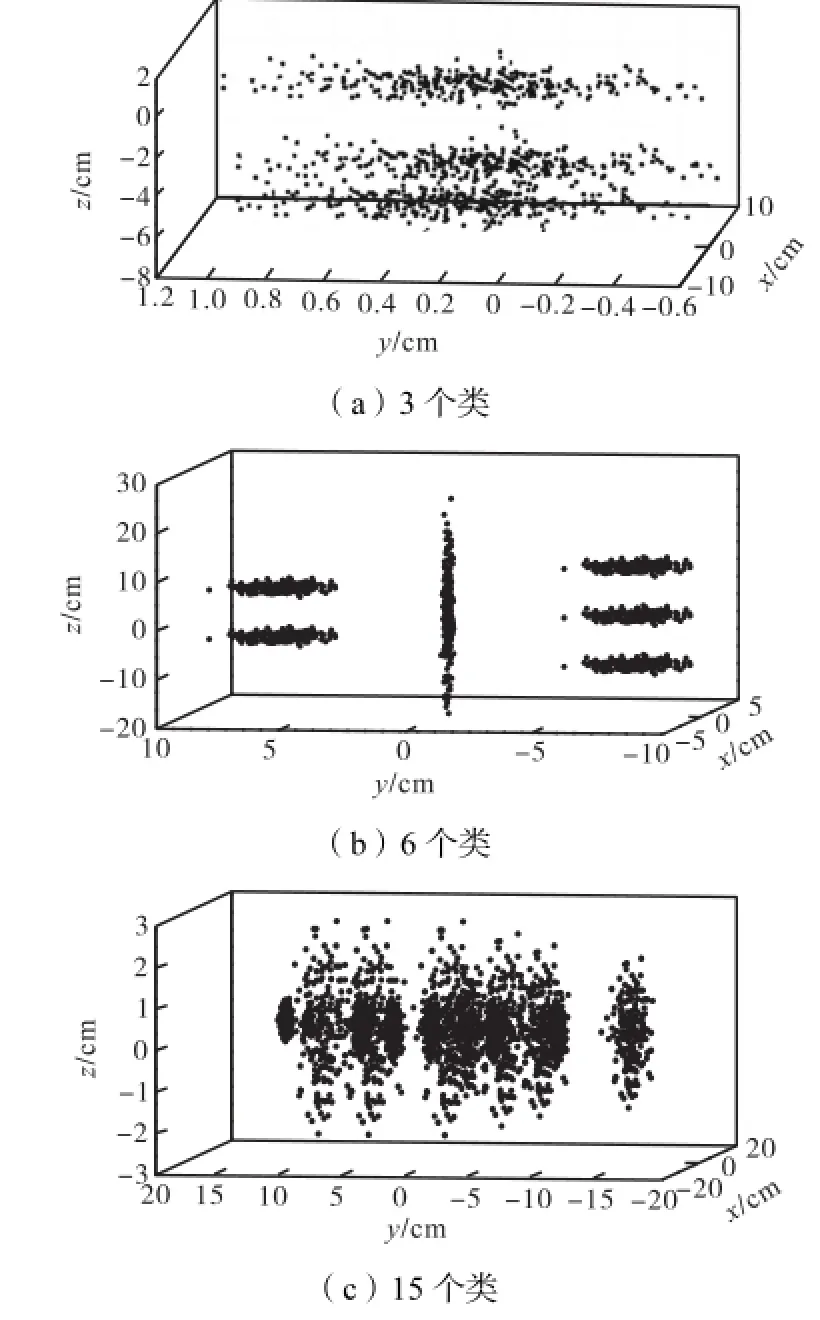
图1 3个带有不同特征的人工数据集Fig.1 Three artificial datasets with different characteristics

(2)Letter数据集．Letter数据集包含20,000个样本，它们分布在26个类中(对应 26个英文字母)，每个样本具有 16个特征．这个数据集不仅仅是一个高维海量样本的数据集，而且不同类的边界也具有高度非线性，即不同类的边界不能用一个线性的超平面分开．

(3)Satim数据集．Satim数据集是一个对观测对象进行卫星多谱扫描所获得的数据集，所有样本分布在 6个类中．每个样本有 36个特征，这个数据集包含6,435个样本．

3.2 实验过程

首先使用 FCM 算法聚类这 6个数据集．在使用 FCM 算法时，本文根据最大隶属度原则来判断每一个样本最终所归属的类．同时，由于 FCM 算法的聚类结果一定程度地依赖于它的初始化过程，本文选择不同初始化条件下最优(目标函数最小)的聚类结果作为最终的结果．3个有效性指标都使用正确性和运行时间 2个指标来评价．这里正确性是指估计类数与真实类数的一致程度；运行时间是指使用每个有效性指标找到最优类数耗费的总时间[18]，并且GDE和 3个指标最大类数的上限都取同样的值以使它们的结果具有可比性．

为了使用 Gerschgorin圆盘直观地分析，首先计算FCM聚类后每个聚类结果的相关矩阵，接着在上述 6个数据集中分别解出所有的特征值．依照正确的类数，本实验测试了当类数分别大于、小于和等于真实类数时，特征值的大小和分布范围．计算相应的 Gerschgorin圆盘半径，图 2～图 7可视化地显示了这些GDE圆盘的分布．

3.3 实验结果分析

图2～图7显示的6个数据集的Gerschgorin圆盘说明如下．如果在FCM算法中所取的类数比真实的类数小，则出现半径较小的圆盘的数目少，此时较大的圆盘数目提供了一个真实类数的下界．特别地，对于数据集1和Iris数据集，这2个计算的圆盘接近同样的半径，无法取舍．这种情况意味着所取的类数(c=2)并不足够大．相反，如果在 FCM 算法中所取类数比真实的类数更大，则许多小半径的圆盘出现．这种情况表明一些类是冗余的，一些原本相似度高的完整的类被不正确地划分成不同类．特别地，当数据集中所取的类数等于真实的类数时，出现半径较小类的数目是最少的．因此，一个数据集中Gerschgorin圆盘的分布可以给使用者提供关于真实类数的新信息．

表1显示了GDE指标在6个数据集中计算出的最优类数，以及与其他3个已有的有效性指标的比较结果．

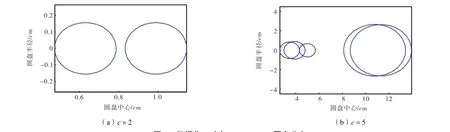
图2 数据集1对应Gerschgorin圆盘分布Fig.2 Distributions of Gerschgorin disks in dataset 1

表1 在6个测试的数据集中3个有效性指标的准确性和稳定性Tab.1 Correctness and stability of the three validity indices in the six datasets

表1的结果表明，如果测试的数据集中的类接近球状，例如数据集1、数据集 2、Iris数据集、Satim数据集等，则FCM算法是最有效的．相应地，每个有效性指标都近似地判断出正确的类数．然而，如果一些类是交叠的，这些指标建议的类数有一些偏差．总体而言，VPB的结果并不比VXB好，与VPE的正确性基本相同．GDE指标比其他3个指标偏差要小．

不同于Iris、Satim和Cancer数据集，Letter数据集包含非线性的类．这导致了有效性指标在估计类数时出现相当大的差别，其本质是FCM算法无论在任何情况下都无法得到正确的划分．迄今，还没有任何一个聚类算法能够正确地划分 Letter数据集中的大多数样本．相应地，也没有任何一个有效性指标能够判断出该数据集中的类数[2,16]．有意义的是，GDE指标能够估计出其正确类数的上界和下界．这比单纯地确定一个类数往往更重要．

表 1进一步显示各个指标的耗费时间．GDE的运算时间包括一次使用聚类、计算相关矩阵、计算特征值 3部分．其中实施 1次聚类是最耗费时间的部分，但对比已有的有效性指标必须遍历所有可能的类数，这里的计算时间已经至少降低 1个数量级．特别地，进一步增加所取的类数，GDE所用的时间不变，其他3个指标所用的时间会线性成比例增长．

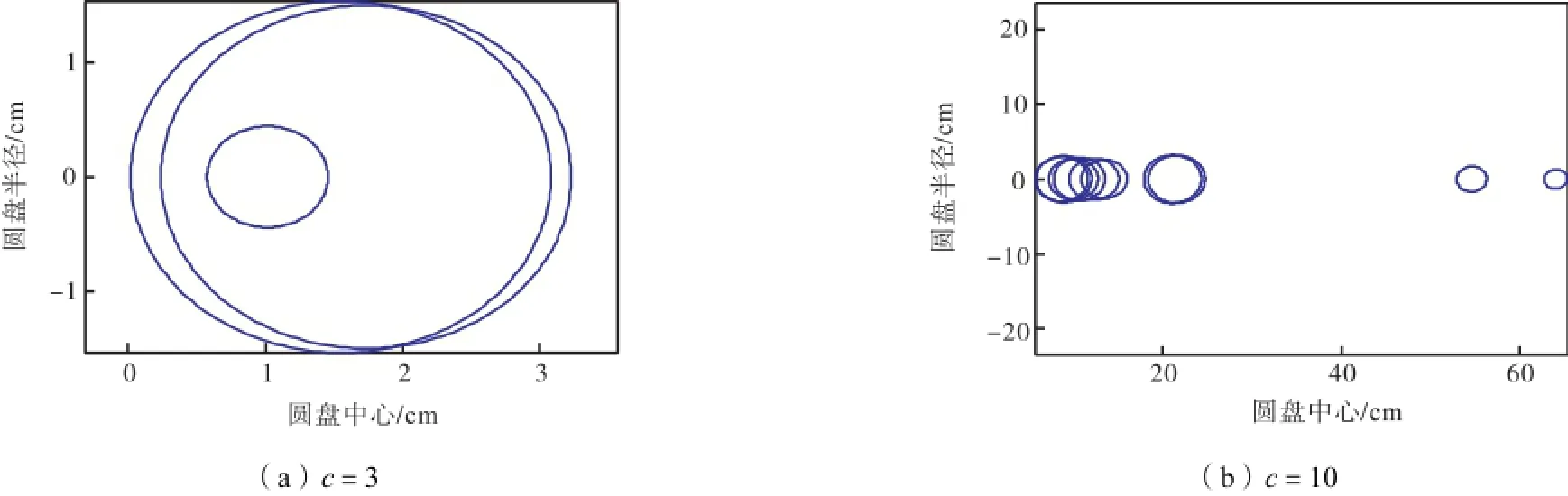
图3 数据集2对应Gerschgorin圆盘分布Fig.3 Distributions of Gerschgorin disks in dataset 2

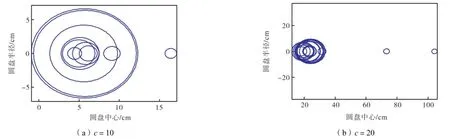
图4 数据集3对应Gerschgorin圆盘分布Fig.4 Distributions of Gerschgorin disks in dataset 3

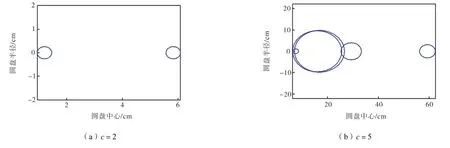
图5 Iris数据集对应Gerschgorin圆盘分布Fig.5 Distributions of Gerschgorin disks in Iris dataset

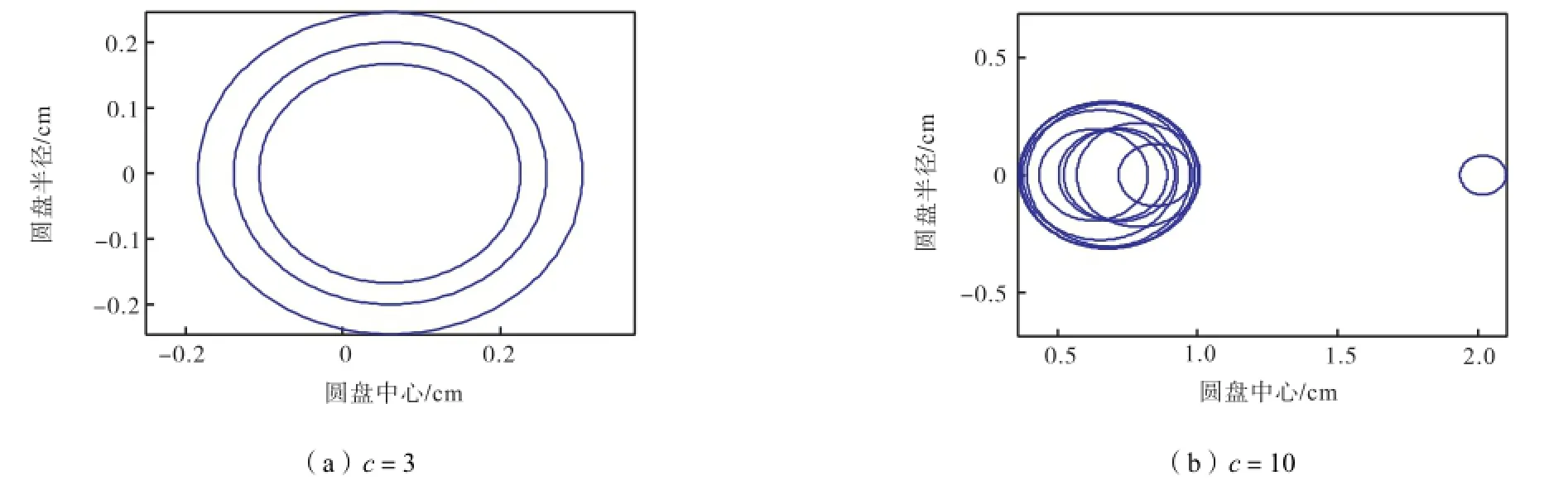
图6 Satim数据集对应Gerschgorin圆盘分布Fig.6 Distributions of Gerschgorin disks in Satim dataset

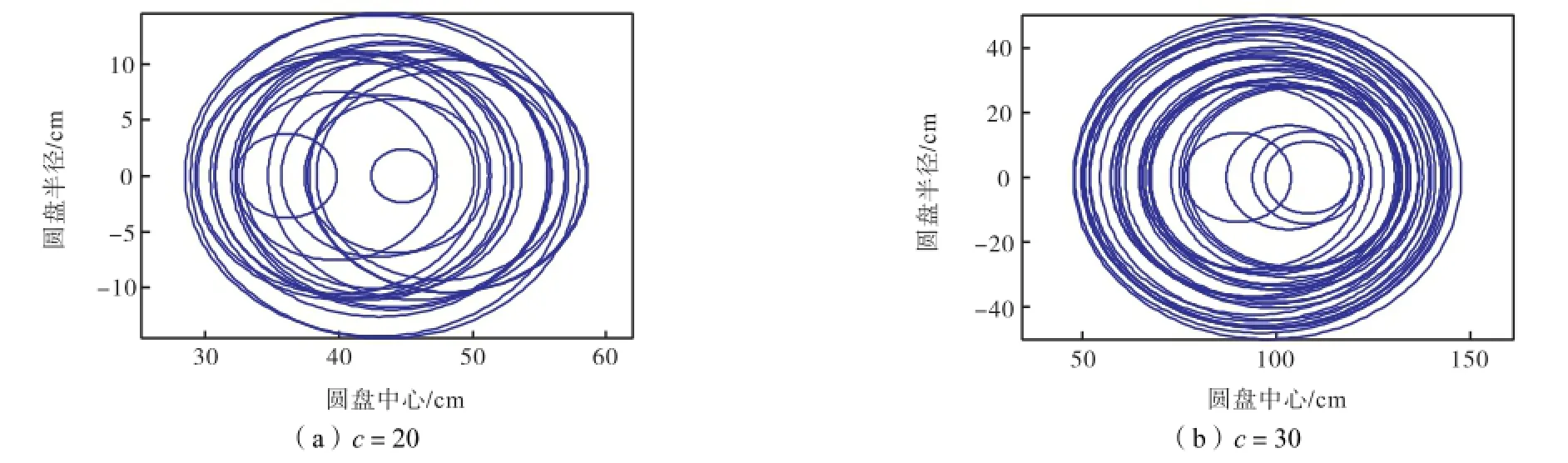
图7 Letter数据集对应Gerschgorin圆盘分布Fig.7 Distributions of Gerschgorin disks in Letter dataset

3.4 一般性分析

本文以一个包含3个类的数据集为例，对特征值与数据集的类的位置关系做更为细致的观察，如图 8所示，随着3个类之间相对位置的变化，表2显示相关矩阵的相对特征值也在变化，这里相对特征值定义为

式中c为在FCM算法中所使用的类数．相对特征值使得在不同数据集中计算出的特征值具有了可比性.从相对特征值的分布可以看出，特征值之间的相对大小反映了类间距离的变化，特征值越大则一个类的分离性越好，并且同一个类的类内相似度越高．不同于已有的有效性指标分别使用类内距和类间距局部度量，GDE可以整体度量类之间的相对位置．同时，有充分的理论依据和泛化能力，这是使用 GDE可以正确判断类数的基本动机．

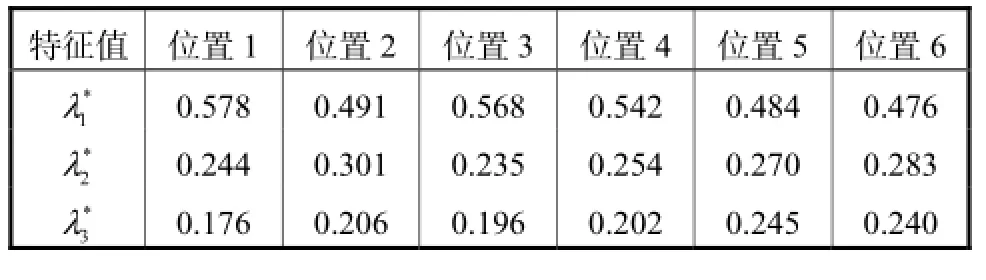
表2 随着3个类相对位置变化特征值的变化Tab.2 Eigenvalue variations of the related matrix with different mutual position variances

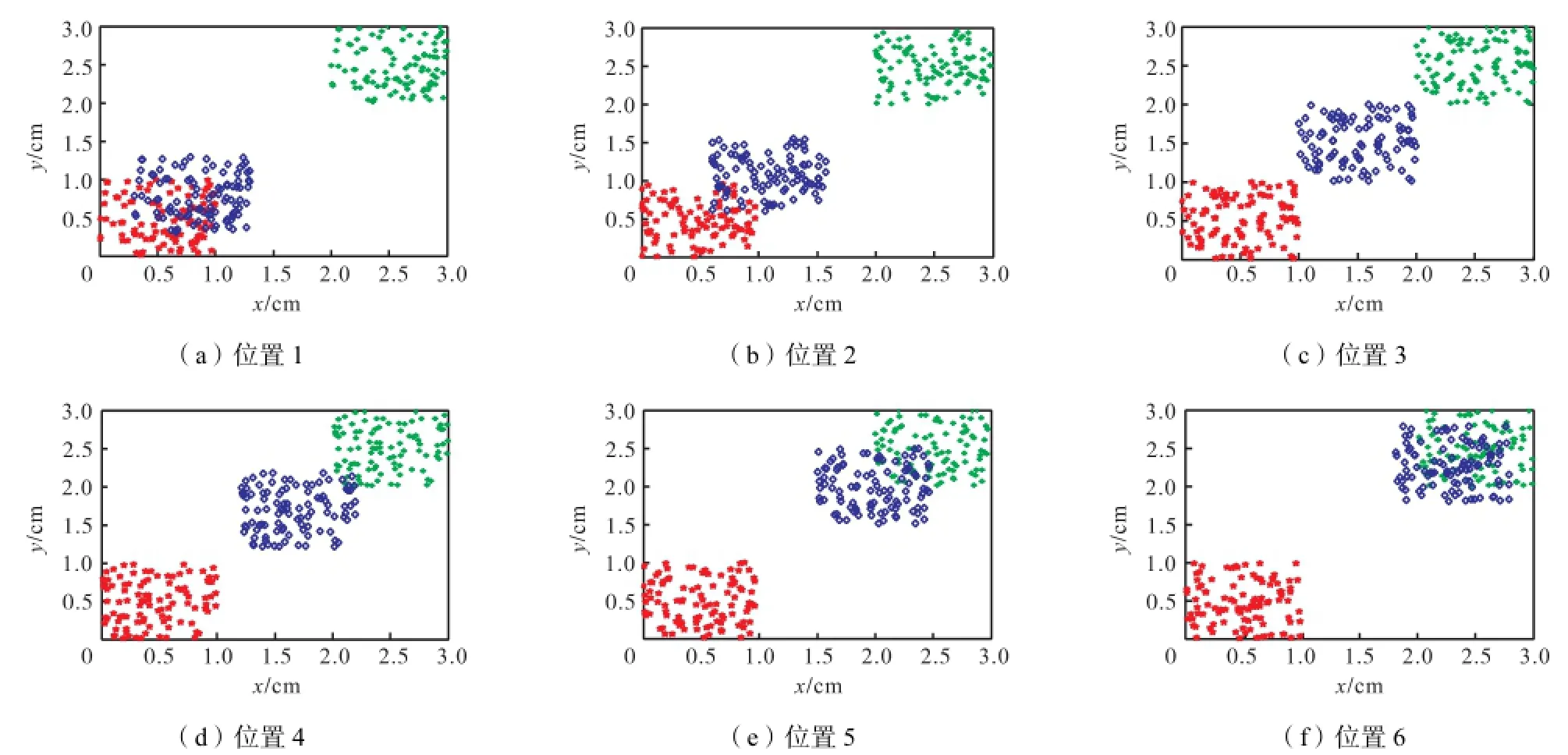
图8 随3个类的相对位置不同相关矩阵的特征值变化Fig.8 Eigenvalue variance of the related matrix in terms of different mutual positions

4 结 语

虽然研究者[1,12-13]已经提出许多有效性指标，但是实际工程界仍然存在着改善这些有效指标效率的迫切需要．本文提出一个新的聚类有效性指标来解决聚类结果的评价问题，这个新的有效性指标评估任何 2个类之间的整体分布而不是局部分布．特别地，本文提出的指标不是遍历式地搜索所有可能的类数，而是在取一个较大的类数后，最少仅仅需要一次聚类就可以估计出最优的类数，从而极大地提高了有效性指标的工作效率．理论和实验结果都证明了本文提出有效性指标是有用的和高效的．

然而，本文提出的有效性指标的工作效率必然受到相关矩阵的定义、计算方式以及聚类结果本身正确性的影响．因此本研究仅仅是一个从根本上提高有效性指标效率的初步尝试，如何更好地构造相关矩阵以及如何选择适当的阈值来确定最终的类数，仍然有待于进一步研究，这些都是将来进一步研究的方向．

［1］ Xu Rui，Wunsch D. Survey of clustering algorithm[J]. IEEE Trans on Neural Network，2005，16(3)：645-678.

［2］ Yue Shihong，Wu T，Liu Zhiqing，et al. Fused multicharacteristic validity index：An application to reconstructed image evaluation in electrical tomography[J]. International Journal of Computational Intelligence Systems，2011，4(5)：1052-1061.

［3］ Bezdek J C，Pal N G. Some new indexes of cluster validity [J]. IEEE Trans on SMC：Cybernetics，1998，28 (3)：301-315.

［4］ MacQueen J B. Some methods for classification and analysis of multivariate observations[C]//The 5th Berkeley Symposium on Mathematical and Probability. Berkeley，USA，1967：281-297.

［5］ Bezdek J C. Pattern Recognition with Fuzzy Objective Function Algorithms[M]. New York：Plenum Press，1981.

［6］ Xie X L，Beni G. A validity measure for fuzzy clustering [J]. IEEE Trans on Pattern Anal Mach Intell，1991，13(8)：841-847.

［7］ Kim D J，Park Y W，Park D J. A novel validity index for determination of the optimal number of clusters [J]. IEICE Trans on Inform Syst，2001，84(2)：281-285.

［8］ Kim D J，Lee K H，Lee D. On cluster validity index for estimation of the optimal number of fuzzy clusters [J]. Pattern Recognition，2004，37(10)：2009-2025.

［9］ Maulik U，Bandyopadhyay S. Performance evaluation of some clustering algorithms and validity indices[J]. IEEE Trans on Pattern Anal Mach Intel，2002，24 (12)：1650-1654.

［10］ Pakhira M K，Bandyopadhyay S，Maulik U. Validity index for crisp and fuzzy clusters[J]. Pattern Recognition，2004，37(3)：487-501.

［11］ Liu Ruochen，Sun Xiaojuan，Jiao Licheng，et al. A comparative study of different cluster validity indexes [J]. Transactions of the Institute of Measurement and Control，2012，34(7)：876-890.

［12］ Yue Shihong，Wang J，Wu T，et al. A new separation measure for improving the effectiveness of validity indices [J]. Information Science，2010，180(5)：411-423.

［13］ Cheng Hao，Vu K，Hua K A. Subspace projection：A unified framework for a class of partition-based dimension reduction techniques[J]. Information Sciences，2009，179(9)：1234-1248.

［14］ 陈黎飞，姜青山，王声瑞. 基于层次划分的最佳聚类数确定方法[J]. 软件学报，2008，19(1)：62-72.

Chen Lifei，Jiang Qingshan，Wang Shengrui. A hierarchical method for determining the number of clusters [J]. Journal of Software，2008，19(1)：62-72(in Chinese).

［15］ Watkins D S. Fundamentals of Matrix Computations [M]. USA：John Wiley & Sons，2002.

［16］ Wang J，Chiang J. A cluster validity measure with a hybrid parameter search method for support vector clustering algorithm [J]. Pattern Recognition，2008，41(2)：506-520.

［17］ Yip K Y，Ng M K，Cheung D W. Input validation for semi-supervised clustering [C]//Proceedings of the 6th IEEE ICDM Workshops. Hong Kong，China，2006：479-483.

［18］ Jiang He，Ren Zhilei，Xuan Jifeng，et al. Extracting elite pairwise constraints for clustering[J]. Neurocomputing，2013，99(1)：124-133.

（责任编辑：孙立华）

Matrix Eigenvalue Analysis-Based Clustering Validity Index

Yue Shihong，Huang Ti，Wang Penglong
(School of Electrical Engineering and Automation，Tianjin University，Tianjin 300072，China)

Many validity indices have been proposed for quantitatively assessing the performance of fuzzy clustering algorithms. But so far these validity indices work with little satisfaction due to their unreasonable structures and low efficiency in applications. In this paper，a Gerschgorin disk estimation-based criterion was proposed to estimate the correct number of clusters. Firstly，a correlation matrix was derived from the fuzzy clustering results，and then the eigenvalue decomposition was performed to obtain all eigenvalues and eigenvectors of the matrix. Finally，based on the classical Gerschgorin disk theorem，the optimal number of clusters was estimated. To validate the proposed criterion in fuzzy clustering，a group of the most used validity indices were applied to three synthetic datasets and three real datasets with different characteristics，and compared with the proposed criterion. The experimental results verify that the proposed criterion can discover the inherit natures among the clustered patterns and suggest more accurate number of clusters.

validity index；Gerschgorin disk；fuzzy cluster；eigenvalue

TK421

A

0493-2137(2014)08-0689-08

10.11784/tdxbz201301016

2013-01-06；

2013-02-01.

国家自然科学基金资助项目(61174017).

岳士弘（1964— ），男，博士，教授.

岳士弘，shyue1999@tju.edu.cn.