基于二阶滑模观测器的无刷直流电机转子位置估计

史婷娜，马银银，王迎发，夏长亮

(天津大学电气与自动化工程学院，天津 300072)

基于二阶滑模观测器的无刷直流电机转子位置估计

史婷娜，马银银，王迎发，夏长亮

(天津大学电气与自动化工程学院，天津 300072)

针对一阶滑模观测器(F-SMO)存在的抖振和相位延迟问题，提出了基于二阶滑模观测器(S-SMO)的线反电势(LBEMF)估计策略，将不连续控制作用在滑模变量的高阶微分上，采用超螺旋算法设计控制率，能较好地削弱抖振，得到连续光滑且无滞后的反电势估计值．针对相反电势法存在的相移问题，采用线反电势过零点直接作为换相点的换相策略．仿真和实验结果表明，所提策略能够准确估计无刷直流电机线反电势，获得准确的转子位置换相点，实现无刷直流电机的无位置传感器控制．

无刷直流电机；二阶滑模观测器；线反电势；换相策略

无刷直流电机由于具有效率高、输出转矩大、响应快、惯性低等诸多的优点，在航空、汽车和家庭应用等方面得到广泛应用[1-3]．传统无刷直流电机的闭环控制需要采用位置传感器来获得转子位置，但位置传感器的存在不仅导致系统成本的提高，而且还影响系统的可靠性和鲁棒性，因此无刷直流电机无位置传感器技术成为目前的一个重要研究方向．近年来，国内外文献介绍的无位置传感器检测方法主要包括相反电势法、磁链法、电感法、续流二极管法等．其中，相反电势法因其简单、实用等特点，成为目前研究的热点[4-6]．

相反电势法通过检测无刷直流电机三相端电压，计算得到电机相反电动势过零点，再相移 /6π 电角度得到无刷直流电机换相位置，其原理简单，实现方便，应用广泛．但在相移角计算过程中，通常依赖于电机速度，尤其是在调速过程中，相移角不准确易造成电机运行性能变差．如何避免相移角计算并直接获得换相点，成为一个新的研究思路．文献[7]提出了一种利用三次谐波检测转子位置的新方法，可检测速度更宽，不需要相移滤波，但在低速下三次谐波严重畸变，导致不能估算转子位置．文献[8]通过对电机模型分析，构造 G函数直接确定无刷直流电机的换相点，扩展了无位置传感器控制调速范围，但系统的计算量增大．

基于滑模观测器的反电势估计策略能准确估算出反电势信号．然而由于其控制作用的不连续性所引起的抖振现象，会导致被控系统出现危险的高频振荡．文献[9]将 sigmoid函数代替开关函数，在一定程度上削弱了抖振，但也不可避免地降低了响应速度，使系统的鲁棒性变差．而低通滤波器的使用会导致相位滞后，难以精确补偿．文献[10]设计了反电势观测器，省去了低通滤波器和相位补偿环节，但估算的反电势存在抖振和噪声，影响准确性．

二阶滑模是解决抖振问题和相位延迟的一种有效的方法，在此方法中，不连续控制并不作用在滑模变量的一阶微分上，而是作用在其高阶微分上，这样不仅保留了一阶滑模控制的所有优点，还可以削弱抖振和相位滞后现象[11-15]．因此本文采用二阶滑模观测器估算电机线反电动势．

本文先采用超螺旋算法设计控制率，再设计二阶滑模微分估计器对电流微分进行估计．此二阶滑模观测器能较好地削弱抖振、得到连续光滑且无滞后的线反电势估计值，提高了无刷直流电机无位置传感器控制的换相精度．通过分析线反电动势过零点与换相时刻的对应关系，提出了采用线反电势过零点直接作为换相点的换相策略，根据虚拟霍耳信号建立无刷直流电机换相逻辑，避免了传统相反电势存在的相移角计算问题．

1 无刷直流电机线电压模型

无刷直流电机三相绕组电压、电流方程表示[16]为

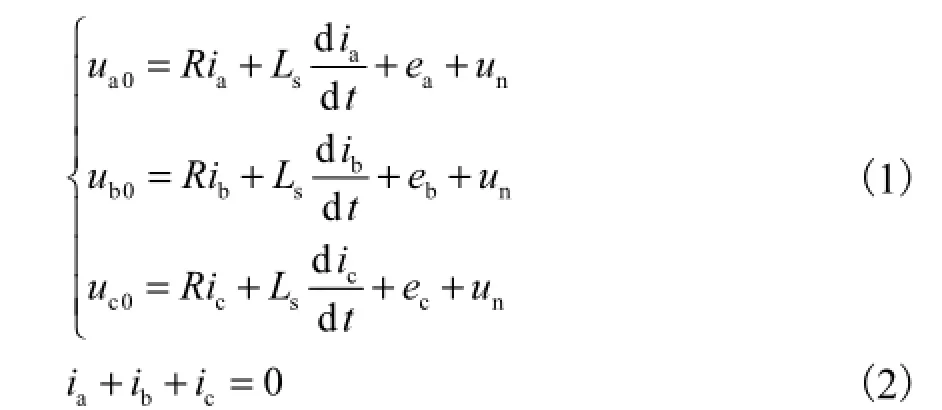
式中：ua0、ub0、uc0分别为三相定子绕组电压；un为电机中性点电压；ia、ib、ic分别为定子相电流；ea、eb、ec为定子相反电势；R和 Ls分别为定子相电阻和等效电感．

由于无刷直流电机中性点电压难以直接检测，将式(1)和式(2)简化为 2个并联的线性无关的一阶电流模型，整理成线电压的状态空间形式为

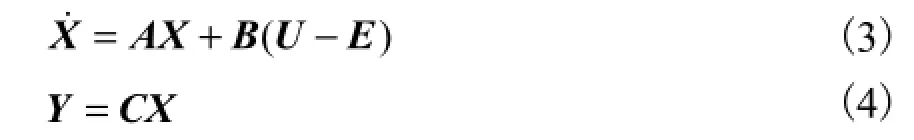
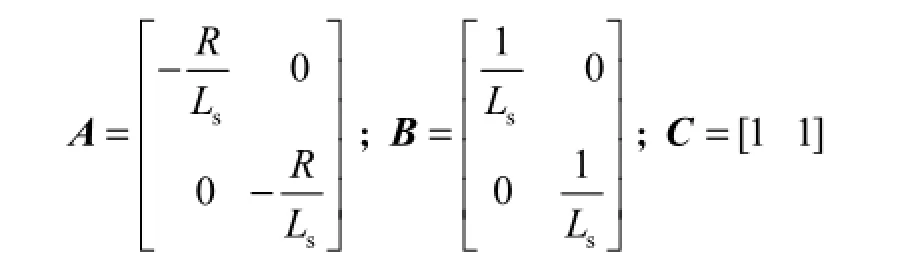
同时，线反电势之间存在关系

由式(3)可知，直接计算能够得到线反电势，但开环计算方式及计算中的电流微分项会导致计算过程中存在一定误差，而采用闭环形式的观测器则可进一步提高线反电势估计精度．

2 反电势滑模观测器

根据式(3)，构建无刷直流电机的二阶滑模观测器

将式(6)与式(3)相减，得到无刷直流电机的状态误差方程为

下面对无刷直流电机的二阶滑模观测器进行分析．

2.1 滑模面选择

将无刷直流电机线电流差作为误差标准，其表示为

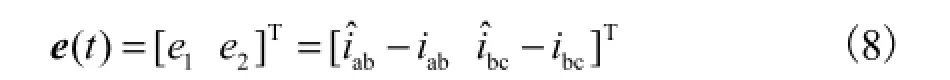
选择二阶滑模观测器的滑模面为

滑模变量的微分表示为

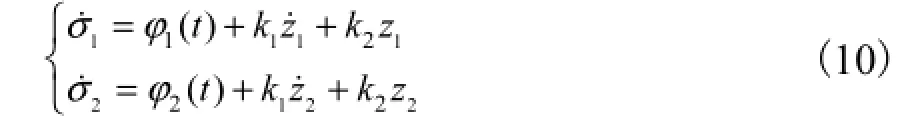
2.2 控制率设计

本文采用超螺旋算法作为二阶滑模观测器中的控制率．超螺旋算法是指在 -σ σ˙平面内，状态轨迹在有限时间内围绕原点螺旋式地收敛到原点．该算法不需要滑模变量的一阶导数和符号信息，离散项出现在控制量的一阶微分上，滑模变量的相关度为 1，能够有效地削弱抖振现象．

采用超螺旋算法的二阶滑模观测器控制率为

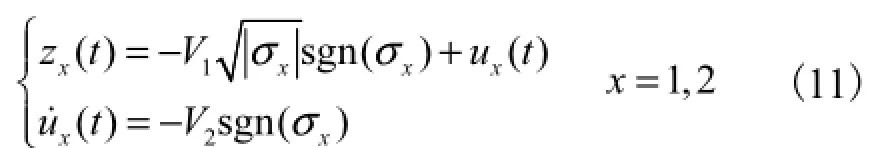
控制率中的参数V1和V2按照约束规则选取，约束规则为

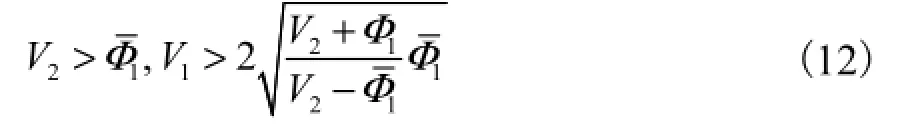
当控制率参数满足以上条件时，超螺旋算法可保证滑模变量在有限时间 tf内收敛到滑模面，即时，保证存在．当滑模变量达到收敛状态时，可准确估算出线反电势信号，估计值为

根据式(5)，可得线反电势eca的估计值

为了便于编程应用，考虑式(11)的 Euler离散化形式，得到

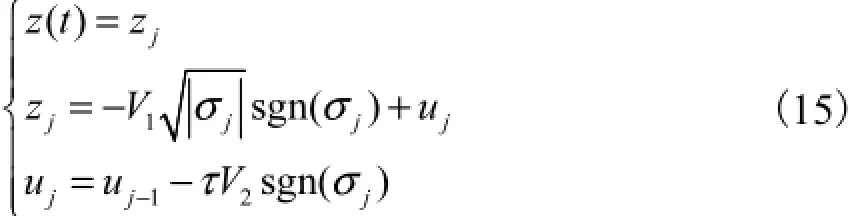
2.3 二阶滑模微分估计器

式(9)需要对电流误差 e(t)求取微分信号，但实际中微分器通常采用一阶差分信号，容易引入噪声干扰．因此，本文采用二阶滑模算法构成微分估计器，估计电流误差微分信号．设定微分估计器输入为电流误差信号 e(t)，电流误差信号微分量为滑模量及其微分量为

采用超螺旋算法建立电流误差信号微分估计器

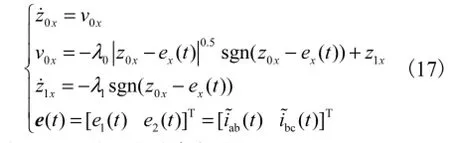
式(16)收敛的充分条件为

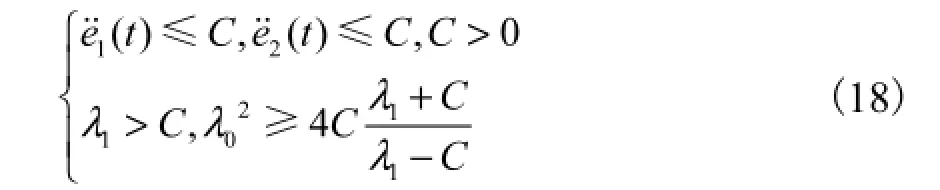
在超螺旋算法控制率作用下，微分估计器经过有限时间后达到收敛，存在

因此，二阶滑模微分器能够较好地得到无刷直流电机线电流误差微分信号．

根据以上分析，设计的无刷直流电机二阶滑模线反电势观测器结构如图1所示．

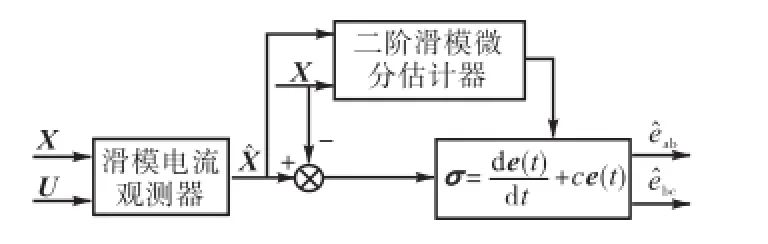
图1 二阶滑模线反电势观测器结构Fig.1 Block diagram of S-SMO

3 线反电势换相策略

无刷直流电机的换相需要确定 6个离散的位置信号，在位置传感器控制中通常由霍耳信号提供6个换相点．而霍耳信号对应的换相点滞后相应相反电势过零点30°电角度，因此相反电势法存在相移角计算问题，造成计算复杂．

本文从线反电势的角度出发，分析霍耳信号与线反电势之间的关系．图 2所示为线反电势过零点与实际霍耳换相信号示意．

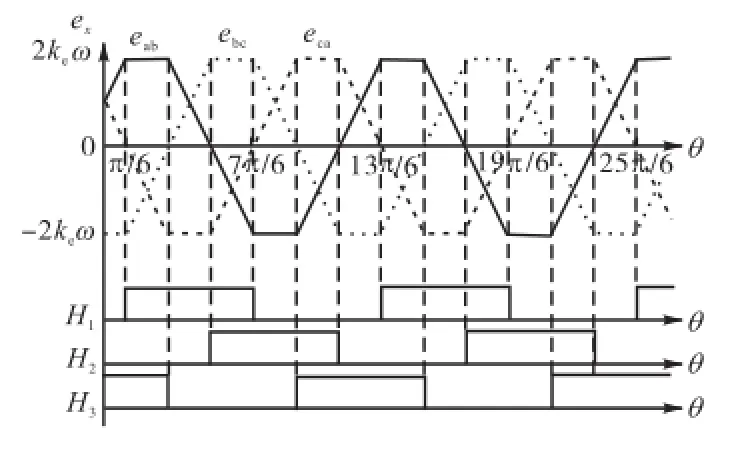
图2 线反电势和霍耳换相信号示意Fig.2 LBEMF and Hall signals

由图2中可以看出，线反电势过零点直接与霍耳信号的换相点对应．若线反电势为正时表示为 1，为负时表示为 0，可得 eab、ebc、eca分别对应H2、H3和(“”表示信号取反)，用虚拟霍耳信号和表示．建立霍耳信号换相逻辑表，如表1所示．

表1 无刷直流电机换相逻辑Tab.1 Commutation logic of BLDCM

4 仿真与实验结果

4.1 仿真结果及分析

利用 Matlab/Simulink建立一阶和二阶滑模观测器仿真模型，电机参数如表2所示．

电机运行在n=2,000,r/min、TL=0.2,N·m条件下，采用一阶滑模观测器对无刷直流电机线反电势估计，反电势估计结果如图3所示．

图3中，实线和虚线分别代表实际线反电势和估算线反电势．一阶滑模观测器由于低通滤波器的使用，反电势估计值存在相位延迟，该延迟会加大电机换相误差，降低电机运行性能．

表2 无刷直流电机参数Tab.2 Parameters of BLDCM

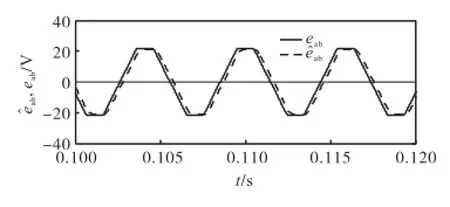
图3 基于一阶滑模观测器的反电势估计值及实际值Fig.3 Estimated and actual LBEMFs of F-SMO

图4为无刷直流电机分别运行在n=200,r/min、n=1,000,r/min、n=2,000,r/min，TL=0.2,N·m条件下，采用二阶滑模观测器得到的线反电势估计值．实线和虚线分别代表实际线反电势和估算线反电势．

由图 4中可以看出，二阶滑模观测器在高、中、低速范围内均能较好地跟踪实际线反电势，能得到连续光滑且无滞后的线反电势估计值，实现无刷直流电机正确换相．

图 5为无刷直流电机在 n=1,000,r/min、TL= 0.2,N·m、电阻Ra增大20%的条件下，线反电势实际值和估计值的仿真结果．

由图5中可以看出，电阻Ra增大20%时，二阶滑模观测器仍能较好地估计出线反电势，表明二阶滑模观测器对电机参数的扰动具有较好的抑制能力．

图 6为 TL=0.2,N·m条件下，电机从 n= 200,r/min变速运行到n=2,000,r/min时，线反电势估计值和功率管换相信号．

图 6(a)表明在变速条件下，二阶滑模观测器仍能准确估算出线反电势，表明二阶滑模观测器具有较好的鲁棒性．图 6(b)中，PT1为根据实际霍耳信号得到的换相信号，为根据本文分析的虚拟霍耳信号得到的换相信号，通过两者对比可以看出，根据线反电动势过零点得到的新的换相策略能准确确定换相位置，实现无刷直流电机无位置传感器控制．

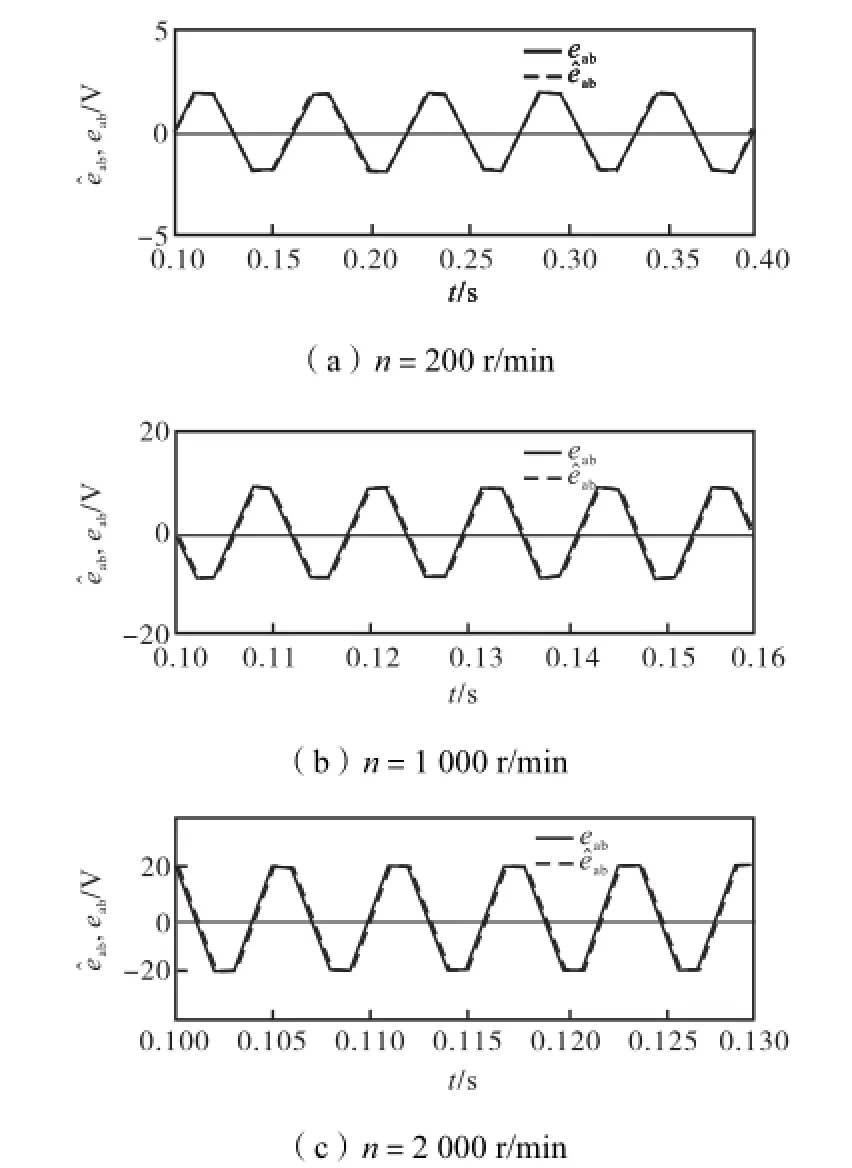
图4 基于二阶滑模观测器的线反电势估计值及实际值Fig.4 Estimated and actual LBEMFs of S-SMO

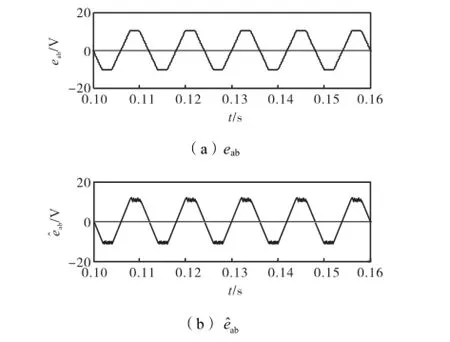
图5 Ra增大20%时的线反电势实际值和估计值Fig.5 Estimated and actual LBEMFs when motor resistance changed to be 1.2Ra

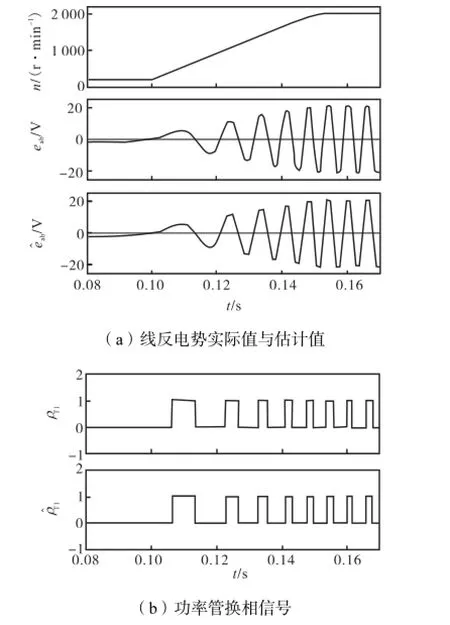
图6 变速运行时的线反电势和换相信号Fig.6 LBEMF and commutation signal at variable speed

4.2 实验结果及分析

为了进一步验证策略的有效性，以TI公司DSP芯片 TMS320F28335为核心控制器建立无刷直流电机实验系统．为了得到较好的实验效果，电压、电流检测均采用霍耳电压、电流传感器，同时设计了 4阶巴特沃斯低通滤波器滤除数据采集中的干扰信号．

图7为n=800,r/min时线电压和换相信号的实验结果．

由图 7中可以看出，换相信号和估计值基本重合，因此基于二阶滑模观测器的线反电势换相策略能够准确地换相，较好地实现无刷直流电机无位置传感器控制．

图 8为线反电势实际值和通过二阶滑模观测器估计得到的线反电势估计值．可以看出，二阶滑模观测器能够较好地估计出无刷直流电机线反电势，且抖振较小，不存在相位滞后．

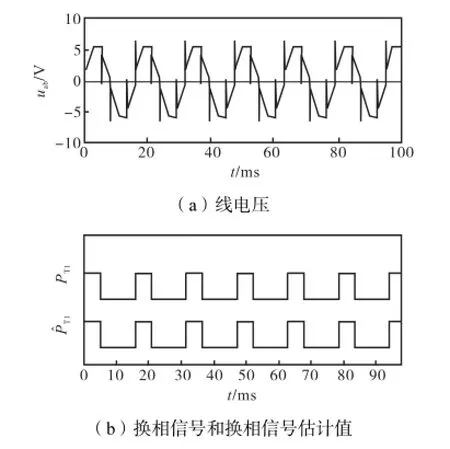
图7 n=800,r/min时的实验结果Fig.7 Experimental results at n=800,r/min

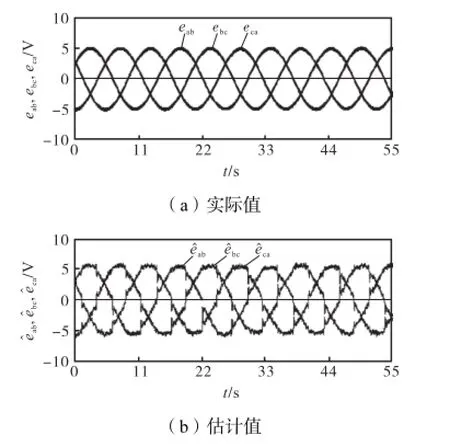
图8 线反电势估计值及实际值Fig.8 Experimental results of estimated and acturalLBEMFs

5 结 论

(1) 二阶滑模观测器不仅保留了一阶滑模观测器的所有优点，且能够较好地削弱抖振，得到连续光滑且无滞后的线反电势估计值．

(2) 通过分析无刷直流电机线反电动势与换相时刻的对应关系，得出线反电动势过零时刻即为换相时刻的结论，建立了虚拟霍耳信号换相逻辑．

(3) 仿真与实验表明，本文策略能够准确估计出无刷直流电机线反电势，获得准确的转子位置换相点，实现了无刷直流电机无位置传感器控制的准确换相，提高了换相精度．

［1］ 张志刚，王 毅，黄守道，等. 无刷双馈电机在变速恒频风力发电系统中的应用[J]. 电气传动，2005，35(4)：61-64.

Zhang Zhigang，Wang Yi，Huang Shoudao，et al. The application study for brushless doubly-fed machine in the variable speed constant frequency generation system[J]. Electric Drive，2005，35(4)：61-64(in Chinese).

［2］ Shi Tingna，Guo Yuntao，Song Peng，et al. A new approach of minimizing commutation torque ripple for brushless DC motor based on DC-DC converter[J]. IEEE Transactions on Industrial Electronics，2010，57(10)：3483-3490.

［3］ Chen Yie-Tone，Chiu Chun-Lung，Tang Zong-Hong，et al. Optimizing efficiency driver comprising phaselocked loop for the single-phase brushless DC fan motor[J]. IEEE Transactions on Magnetics，2012，48(5)：1937-1942.

［4］ Shao Jianwen. An improved microcontroller-based sensorless brushless DC motor drive for automotive applications[J]. IEEE Transactions on Industry Applications，2006，42(5)：1216-1221.

［5］ Imoru O，Tsado J. Modelling of an electronically commutated(brushless DC)motor drives with back-emf sensing[C] //16,th IEEE Mediterranean Electrotechnical Conference(MELECON). Yasmine Hammamet，Tunisia，2012：828-831.

［6］ Damodharan P，Vasudevan K. Sensorless brushless DC motor drive based on the zero-crossing detection of back electromotive force (EMF) from the line voltage difference[J]. IEEE Transactions on Energy Conversion，2010，25(3)：661-668.

［7］ 韦 鲲，任军军，张仲超. 三次谐波检测无刷直流电机转子位置的研究[J]. 中国电机工程学报，2004，24(5)：163-167.

Wei Kun，Ren Junjun，Zhang Zhongchao. Research on the scheme of sensing rotor position of BLDCM based on the third harmonic component[J]. Proceedings of the CSEE，2004，24(5)：163-167(in Chinese).

［8］ Kim Tae-Hyung，Ehsani M. Sensorless control of the BLDC motors from near-zero to high speeds[J]. IEEE Transactions on Power Electronics，2004，19(6)：1635-1645.

［9］ Kim Hongryel，Son Jubum，Lee Jangmyung. A highspeed sliding-mode observer for the sensorless speed control of a PMSM[J]. IEEE Transactions on Industrial Electronics，2011，58(9)：4069-4077.

［10］ Qiao Zhaowei，Wang Yindong，Shi Tingna，et al. New sliding-mode observer for position sensorless control of permanent-magnet synchronous motor[J]. IEEE Transactions on Industrial Electronics，2013，60(2)：710-719.

［11］ Damiano A，Gatto G L，Marongiu I，et al. Secondorder sliding-mode control of DC drives[J]. IEEE Transactions on Industrial Electronics，2004，51(2)：364-373.

［12］ 孙宜标，杨 雪，夏加宽. 基于二阶滑模的永磁直线同步电机鲁棒速度控制[J]. 电工技术学报，2007，22(10)：35-41.

Shun Yibiao，Yang Xue，Xia Jiakuan. Robust speed control of permanent-magnet linear synchronous motor based on the second order sliding mode[J]. Transactions of China Electrotechnical Society，2007，22(10)：35-41(in Chinese).

［13］ 凌 睿，柴 毅. 永磁直线同步电机多变量二阶滑模控制[J]. 中国电机工程学报，2009，29(36)：60-66.

Ling Rui，Chai Yi. Multi-variable second order sliding mode control for PMLSM[J]. Proceedings of the CSEE，2009，29(36)：60-66(in Chinese).

［14］ Beltran B，Ahmed-Ali T. Second-order sliding mode control of a doubly fed induction generator driven wind turbine[J]. IEEE Transactions on Energy Conversion，2012，27(2)：261-269.

［15］ Evangelista C，Puleston P，Valenciaga F，et al. Lyapunovdesigned super-twisting sliding mode control for wind energy conversion optimization[J]. IEEE Transactions on Industrial Electronics，2013，60(2)：538-545.

［16］ 王迎发．无刷直流电机换相转矩波动抑抑制与无位置传感器控制研究[D]. 天津：天津大学电气与自动化工程学院，2011．

Wang Yingfa. Research on Commutation Torque Ripple Reduction and Sensorless Control of Brushless DC Motor[D]. Tianjin：School of Electrical Engineering and Automation，Tianjin University(in Chinese)．

（责任编辑：孙立华）

Rotor Position Estimation of Brushless DC Motor Based on Second-Order Sliding Mode Observer

Shi Tingna，Ma Yinyin，Wang Yingfa，Xia Changliang
(School of Electrical Engineering and Automation，Tianjin University，Tianjin 300072，China)

To solve the chattering and phase delay problems existing in first-order sliding mode observer(F-SMO)，line back-electromotive force (LBEMF)was estimated by a second-order sliding mode observer(S-SMO)which applied the discontinuous control function on the high order differential of sliding mode variable and employed a supertwisting algorithm in control design. To deal with the phase shift problem，a new commutation strategy based on LBEMF zero-crossing point was proposed. Simulation and experiment results show that the sensorless control system can estimate LBEMF exactly，and accurate rotor position commutation point is gained.

brushless DC motor；second-order sliding mode observer；line back-electromotive force (LBEMF)；commutation strategy

TM383

A

0493-2137(2014)08-0697-06

10.11784/tdxbz201301003

2013-01-05；

2013-04-26.

国家自然科学基金重点资助项目(51037004).

史婷娜（1969— ），女，博士，教授.

史婷娜，motor@tju.edu.cn.