吹填土真空固结变形特性的室内试验
2014-06-05邱长林闫澍旺纪玉诚天津大学建筑工程学院天津300072
邱长林,牛 飞,闫澍旺,纪玉诚(天津大学建筑工程学院,天津 300072)
吹填土真空固结变形特性的室内试验
邱长林,牛 飞,闫澍旺,纪玉诚
(天津大学建筑工程学院,天津 300072)
为了研究吹填土在真空预压作用下的固结特性和应力应变关系,设计了室内试验装置.在该装置中,吹填土作为一个土单元进行真空固结,通过测量该吹填土体单元在分级真空荷载作用下的体应变和轴向应变过程来研究吹填土的固结变形特性.试验结果表明,吹填土在真空荷载作用下的固结为等向固结,土体的变形各向同性.各级真空荷载作用下,土体的体应变和轴向应变与真空压力之间呈双曲线关系,孔隙比和真空压力的对数之间呈线性关系,且与初始含水率无关.分级荷载下固结时间和变形量表明,超软土在初始阶段的固结在整个固结过程中占据主导作用.试验结果可用于建立吹填软土在真空荷载作用下的应力应变关系和预测真空加固吹填土的固结沉降值.
真空荷载;吹填土;固结特性;应力应变关系;室内试验
我国沿海地区围海造陆工程一般是将疏浚港口航道的淤积物吹填到低洼处,然后进行加固处理以形成陆域.吹填施工刚完成时,吹填淤泥一般含水量很高,处于流动状态,需要进行加固处理,而真空预压是处理吹填土最有效的地基加固方法.早期的做法是在吹填完毕后,经过2~3年的晾晒,在地表形成一个硬壳层,经进一步处理后能够满足插板机械的承载力要求,然后进行真空预压加固.近年来,为了加快吹填地基的利用速度,采用了在吹填土表面吹填一定厚度的粉细砂或通过浅层加固形成硬壳层,使之可以满足直接插板施工的条件,这样新近吹填土地基在吹填完成后即可进行真空预压.总之,经过多年的实践,真空预压技术在施工方面已相对成熟.
与施工工艺不同,真空预压吹填土的机理和数值分析上还很不完善.为了研究真空荷载作用下软土的固结变形特性,研究人员进行了室内试验研究.陈环等[1]用一维负压固结仪进行了抽气试验,得出了在相同的压差下加固效果基本相同的结论;闫澍旺等[2]用三轴仪进行了正负压对比试验,认为在正负压作用下土体的固结过程是基本相同的;张诚厚等[3]用固结仪研究了正负压力下土样剪切强度增长的情况;李丽慧等[4]在三轴仪上对真空排水预压下土体变形特性进行了应力路径分析,测定软土地基在真空预压加固后应力路径的改变对沉降量的影响;Mahfouz等[5]、吴桂芬等[6]通过三轴试验装置对比了真空和正压荷载作用下软土的固结过程.高志义等[7]利用离心模型试验、林丰等[8]和闫澍旺等[9]利用模型槽对土体真空固结特性进行了研究.这些室内研究都没有针对真空荷载作用下土体的应力应变特性进行研究.
由于吹填土在吹填前为流动的泥浆状态,含水量高、压缩性比较大,经过真空预压后直接成为固态土体,即在加固过程中吹填土经历了从液态到固态的变化过程,其承受的应力和孔隙比有了显著的改变,因此其在真空预压过程中会发生很大的沉降;另外,由于吹填土未经过前期的自重应力固结阶段,而自重应力和真空压力的力学特性差异比较大,导致吹填土的物理力学特性和一般的软土相比有较大的差异.随着造陆区域范围的扩展,原地面的标高越来越低,使得吹填土越来越厚,现在已经接近10,m,这导致理论计算的孔压消散和变形结果与实际观测结果有很大差距.
为了解决理论和实际结果不一致的现象,本文设计了真空荷载作用下吹填土的固结特性室内试验.在该试验中,吹填土作为一个土单元在真空荷载作用下进行固结,通过测量其体积变形和轴向变形来研究吹填土在真空荷载作用下的固结过程和固结特性,从而为建立真空荷载作用下吹填土的本构关系并计算吹填土地基的固结变形提供依据.
1 试验方案
1.1 试验装置
为了研究高含水量的吹填土在真空压力作用下的固结过程,进而研究其在真空荷载作用下的应力应变关系,本研究设计加工了模型试验装置,如图1所示.该试验装置主要由土样室、真空控制系统、量测系统等组成.土样室是安装试样并使真空压力作用于试样的装置,由金属上盖、有机玻璃筒和底座组成.真空控制系统用于向土样提供真空压力,由真空泵、真空罐、真空电接点和真空调压阀组成,其中真空电接点用于控制真空泵的启动,而真空调压阀用来精确控制施加于土样的真空压力值,本试验装置中的真空调压阀采用日本SMC公司生产的10-IRV10系列真空调压阀,该调压阀可调节的真空压力范围为-100~-1.3,kPa,调节精度为0.13,kPa.量测系统由量管、百分表和真空表组成,其中量管通过土样室底座和土样室内的水体相连,用于测量土样室中有机玻璃筒内水的体积变化,从而间接测出土体的体积变形量;百分表通过土样室上盖中央的不锈钢杆和土样顶部相连,用于测量土体的轴向变形;真空表用于测量作用于土样底部和顶部的真空压力.
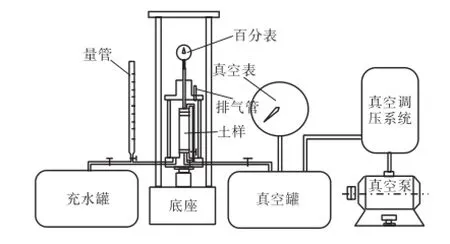
图1 试验装置Fig.1 Experimental device
试验土样为圆柱形,其直径为35,mm,高为80,mm.土样放置于土样室的底座上,其顶部和底部放置有透水石和土工布.试样外套橡皮膜,橡皮膜两端与底座及试样帽用橡皮圈扎紧,使试样和土样室中的水体隔离开.土样两端通过土样室底座中的管路和真空控制系统相连,因此在真空压力作用下,土样中的水可以通过土工布和透水石从顶部和底部排出,土体进行固结.
1.2 试验方法
试验采用一个土样分级加荷的方法,即试验时对不同初始含水率的土样分级施加真空压力.施加每一个等级的真空压力后测量试样在不同时刻的体积变形量和竖向变形量,直到土样在该荷载作用下固结完成.然后施加下一级荷载进行真空固结直至试验结束.土样在真空压力作用下固结完成的标准采用体积变形稳定的判断方法,本试验中取土样在连续两个小时内每一小时土体的体积变化量等于或小于0.1,mL为其固结完成的标准.每一个试样施加的真空压力为-10,kPa、-25,kPa、-40,kPa、-60,kPa和-80,kPa共5级.
试验用土取自塘沽,为淤泥质黏土,其塑限为28%,液限为51%,塑性指数为23.试验的土样制备采用土膏法[10].配置后土样的初始含水率分别为70%、80%和92%.
2 体积变形
2.1 体积变形过程及试验结果
将固结过程中土体体积变化量除以土样初始体积即可得到土样在固结过程中体应变随时间的变化曲线,结果如图2所示.从图中可以看出,在每一级真空压力作用下,土体的体应变先是有一个快速增长的过程,然后随着固结时间的增加,增长速度逐渐降低,最后趋近于0.该图还表明,在荷载为10,kPa情况下,初始含水率为70%、80%和92%的土体固结后的体应变分别为9.4%、19.3%、28.1%,占总固结体应变的比例为34.4%、57.4%、71.1%;固结时间为15.15,h、43.5,h、38,h,占相应土样总固结时间的23.5%、42.4%、49.3%.由此可以看出,高含水率吹填土在初始阶段的固结是整个吹填土固结阶段的主要阶段,且随着土样初始含水率的增加,固结导致的体应变在整个固结过程中所占的比例也越大.但是由于采用该方法制作的土样高度并不一致,即土体的固结路径长度不同,因此土体的总固结时间并不是按含水率的增加而增加的,其中最初含水率为92%的试验土样高度最小,因此其固结时间比含水率为70%和 80%的土样固结时间少.
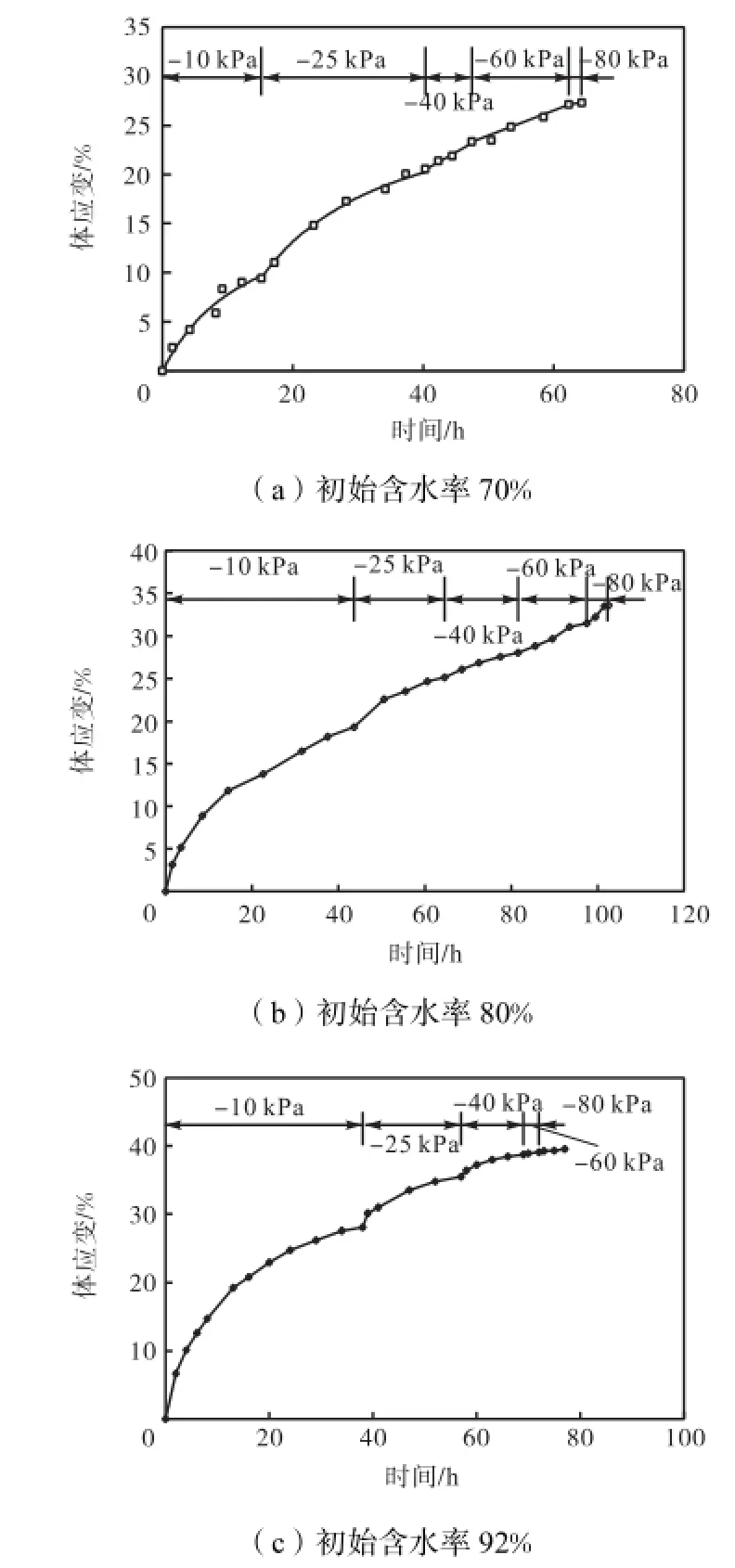
图2 体应变变化曲线Fig.2 Curve of volume strain change
2.2 体应变和真空压力的关系
根据土样在不同等级真空压力下稳定的体应变,可以得到土样体应变和真空压力之间的关系,如图3所示.由于在真空压力固结过程中,土体总应力保持为0不变,而土中的孔隙水压力在不断减少,根据有效应力原理可知,在该过程中土体的有效应力即为孔隙水压力的减少值,即等于施加的真空压力,因此图3也是土体在真空压力作用下体应变和有效压力之间的关系曲线.从图3可以看出,体应变和真空压力之间呈非线性关系,在真空压力比较小时,土体的体应变增长速度比较快,随着真空压力的增加,土体的体应变增加速度减小.该关系可以用双曲线方程表示为

式中:εv为体应变;p为真空压力绝对值;A、B为与初始含水率有关的拟合参数.本试验中,对应于初始含水率为70%、80%和92%的土体,参数A分别为0.366、0.366、0.426,B分别为23.04、10.02、5.02.
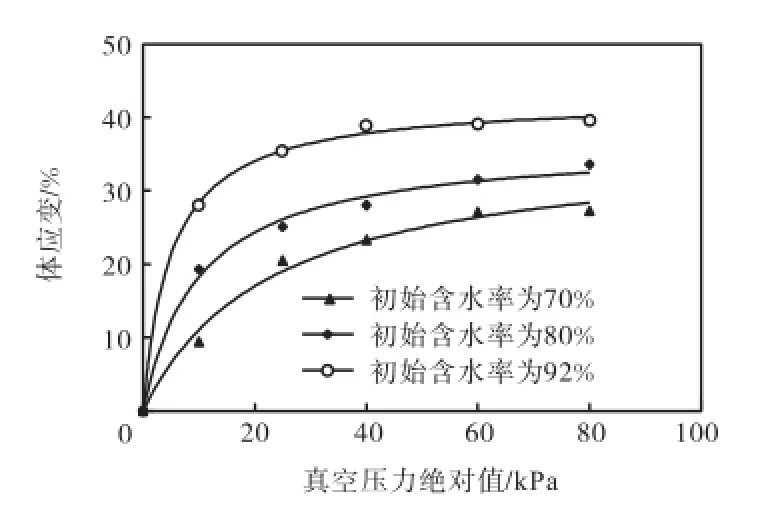
图3 体应变和真空压力的关系Fig.3Relationship between volume strain and vacuum pressure
3 轴向和径向变形
3.1 轴向变形时程
在本试验中,初始含水率为70%的土样没有测量轴向变形,将其余两个土样测得的轴向变形量除以土样初始高度,即可得到土体的轴向应变变化过程,试验结果如图4所示.从图中可以看出,轴向应变曲线和体应变曲线相似,即在每一级真空荷载作用下,土体的轴向应变先是有一个快速增长的过程,然后随着固结时间的增加,增长速度逐渐降低,最后趋近于0,且随着土样初始含水率的增加,第一级荷载的固结所需的时间增加,同时固结导致的体应变在整个固结过程中所占的比例也越大.
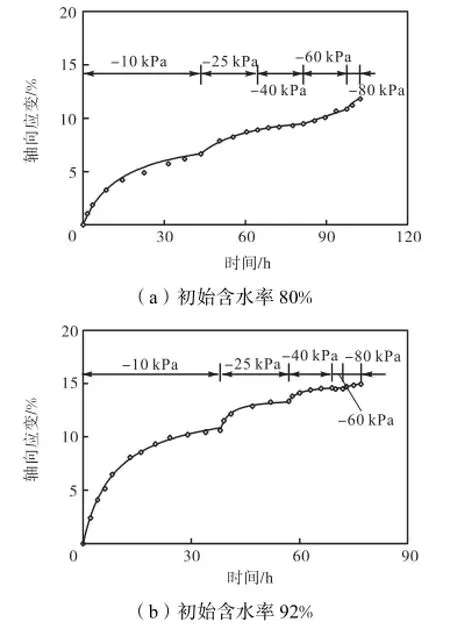
图4 轴向应变变化曲线Fig.4 Curve of axial strain change
3.2 轴向变形和径向变形与真空压力的关系
根据图4可以得到土体轴向应变和真空压力之间的关系如图5所示.从图中可以看出,与体应变的规律相似,土体的轴向应变和真空压力之间也为非线性关系,即随着真空压力的增加,土体的轴向应变增加,且增加速率逐渐减小.该关系曲线也可以采用公式(1)所示的双曲线方程来表示.
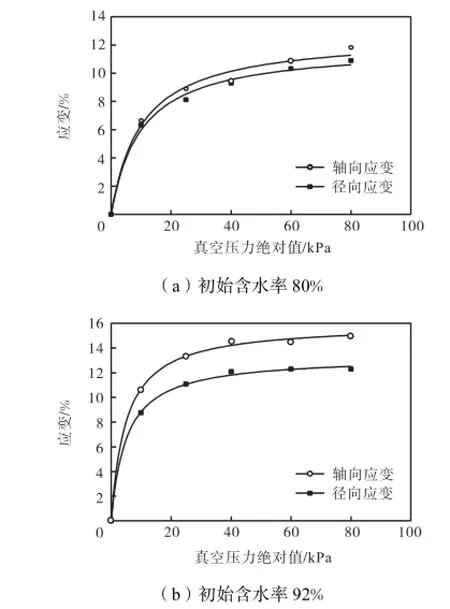
图5 应变和真空压力关系Fig.5 Relationship between strain and vacuum pressure
在轴对称变形条件下,土体径向变形为

式中εa和εr分别为轴向应变和径向应变.根据式(2),图3和图5可以得到径向应变与真空压力之间的关系.同时本次试验中还有一组含水率为88%的土样在各级真空荷载作用下没有充分固结,根据式(2)得到该组土样在不同时刻的轴向应变和径向应变之间的关系,如图6所示.从图5和图6可以看出,在真空荷载作用下,土体会产生一定的径向变形,该变形也随着土体真空压力的增加而增加,因此在真空预压工程中,超软土地基将会发生侧向变形,这已被大量的模型试验所证明.
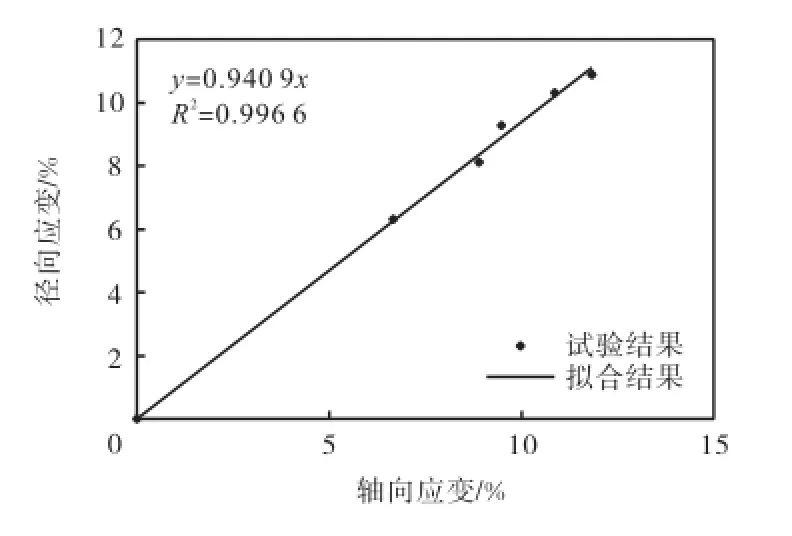
图6 轴向应变和径向应变的关系(初始含水率88%)Fig.6Relationship between axial strain and radical strain(initial water content 88%)
从图5(a)和图6还可以看出,在相同的真空压力作用下,两个土体的轴向应变和径向应变基本相同,这说明土体在真空荷载作用下的固结为等向固结.而图5(b)中初始含水率为92%的土体轴向变形略大于径向变形,初步分析认为可能是由于土体的初始含水率较大,土样自重作用下的自身稳定性较差,土样在制作安装后施加真空压力之前在自重作用下会发生一定的轴向变形,这一部分轴向挤压变形使土样变得更胖,这导致土体的轴向变形大于土体的径向变形.该结果表明,和天然固结的软土不同,超软土在真空荷载作用下的固结中各向异性问题影响较小.
4 孔隙比变化规律
试验结束后,将土样近似均匀地分为8小份,测出每一小份土样的含水率,即可得到试验结束后土样含水率沿高度分布,如图7所示,其中横坐标为每一小份土样在原土样中的位置,每一小份用一个点表示,底部位置为0,顶部位置为7.从图7可以看出,土体在真空固结结束后,不同初始含水率的土体在相同的真空压力作用下固结结束后的含水率基本相同.
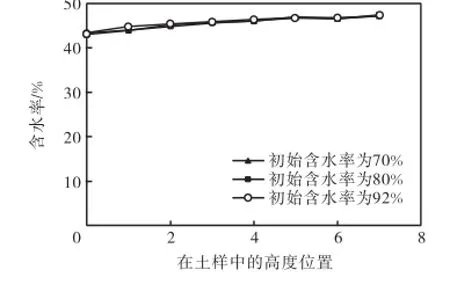
图7 固结结束时土样含水率分布Fig.7 Distribution of water content along sample after consolidation
从图7中可以看出,在固结结束后,土样的顶部和底部含水率并不完全相同,这说明在本次试验中土样的顶部和底部的真空压力并不完全相同,这主要是由于在本试验中,土样顶部和底部的真空压力都是由同一条管线从恒压罐中引出,该管线到达土样的底部阀门后再通过附加的一条管线通到土样的顶部阀门.该附加管线导致的真空压力损失就是土样底部和顶部的真空压力差异值.
对于饱和土体,可以认为所有的体积变化都是由于水的体积变化导致,即土体颗粒的流失以及土颗粒和水的压缩变形可忽略不计,则根据图3和图7,可以得到固结结束后土样含水率和真空压力的关系,如图8所示.从图8可以看出,随着真空压力的增加,土体的含水率在逐渐变小,因此土体的孔隙率也逐渐变小,即土体得到了压缩.随着真空压力的增加,含水率和真空压力关系曲线的斜率逐渐变小,即真空压力的加固效果逐渐减小.从图8还可以看出,不同初始含水率的土体,在相同的真空压力下固结结束后,其含水率基本相同.该结果表明,当固结时间到达一定值、土体的固结基本完成后,试图通过增加固结时间的方法来提高土体的固结效果是不可行的.
对于饱和土,有

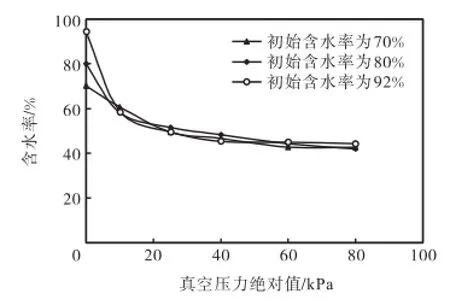
图8 含水率和真空压力的关系Fig.8 Relationship between water content and vacuum pressure
式中:e为孔隙比;w为含水率;Gs为土体的比重.通过式(3),可将图8转换成孔隙比和真空压力之间的关系,并在半对数坐标系中绘出,结果如图9所示.从图中可以看出,对于不同初始含水率的土体,在相同的真空压力作用下,土样的孔隙比都相同,即土体的孔隙比和真空压力之间存在一一对应的关系.
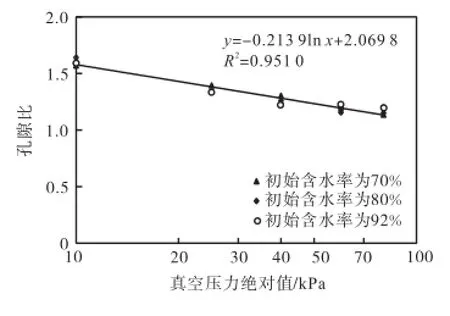
图9 孔隙比和真空压力之间的关系Fig.9 Relationship between void ratio and vacuum pressure
图9 结果还表明,孔隙比和真空压力的对数之间呈线性关系,该关系可以表示成

式中:Cc为压缩指数;e10为真空压力为-10,kPa时土体的孔隙比.在该试验中,Cc和e10分别为-0.49和1.58.该关系式拟合的相关系数R2=0.951,0.
由文献[11]可知,在正压作用下,超软土的e10和液限时的孔隙比的关系为

式中:eL为土体在液限时的孔隙比;α为一个常数,其范围为0.90~1.32.本次试验得到在真空荷载作用下的α=1.12,结果也满足这个规律.
5 结 论
针对真空预压直接加固吹填土过程中吹填土的固结特性,本文设计了真空预压加固吹填土的室内试验,从土单元的尺度研究了吹填土在真空荷载作用下的固结变形特性.通过试验得到如下结论.
(1) 真空荷载作用下吹填土的固结过程中初始阶段的固结起主要作用.随着初始含水率的增加,该阶段固结所需的时间增加,且该阶段固结导致的体应变在整个固结过程中所占的比例也越大.
(2) 真空压力为一体积力.在该压力作用下,吹填土竖向的应变和径向应变相等,且为体应变的1/3,即土体的变形为等向变形,因此真空预压固结吹填土不仅会产生较大的沉降,还会导致地基中出现较大的水平位移.同时与天然软土不同,真空荷载作用下吹填土的各向异性现象不显著.
(3) 在真空压力作用下,吹填土的最终孔隙水压力和真空压力有一一对应关系,这表明通过增加预压时间来提高固结效果的方法不可行.
(4) 真空荷载作用下,固结结束后吹填土的孔隙比和真空压力的对数值之间为线性关系,这与正压力荷载作用下土体的固结规律相同.
本文主要考虑了真空压力对于吹填土的作用机制和效果分析,在实际工程中当吹填土厚度较大时,还需考虑吹填土自重固结的影响.
[1] 陈 环,鲍秀清. 负压条件下土的固结有效应力[J].岩土工程学报,1984,6(5):39-47.Chen Huan,Bao Xiuqing. Consolidation effective stresses in soil under the negative pressure condition[J]. Chinese Journal of Geotechnical Engineering,1984,6(5):39-47(in Chinese).
[2] 闫澍旺,陈 环. 用真空加固软土地基的机制与计算方法[J]. 岩土工程学报,1986,8(2):35-44.Yan Shuwang,Chen Huan. Mechanism and calculation methods of vacuum stabilization of soft clay[J]. Chinese Journal of Geotechnical Engineering,1986,8(2):35-44(in Chinese).
[3] 张诚厚,王伯衍,曹永琅. 真空作用面位置及排水板间距对加固效果的影响[J]. 岩土工程学报,1990,12(1):45-52.Zhang Chenghou,Wang Boyan,Cao Yonglang. The influence of vacuum location and the spacing of drain well on the effect of preloading improvement[J]. Chinese Journal of Geotechnical Engineering,1990,12(1):45-52(in Chinese).
[4] 李丽慧,王 清,王剑平,等. 真空排水预压下土体变形的应力路径分析[J]. 工程地质学报,2001,9(2):170-173.Li Lihui,Wang Qing,Wang Jianping,et al. Analysis of stress path soil’s deformation under the vacuum drainage preloading[J]. Journal of Engineering Geology, 2001,9(2):170-173(in Chinese).
[5] Mahfouz A H,Liu Hanlong,Chiu C F,et al. Laboratory study for effects of vacuum preloading on physical and mechanical properties of soft clayey soils [J]. Journal of Southeast University:English Edition,2005,21(1):82-87.
[6] 吴桂芬,高玉峰,魏代现,等. 真空和堆载两种预压法的室内试验研究[J]. 岩土力学,2005,26(增):95-98.Wu Guifen,Gao Yufeng,Wei Daixian,et al. Study on laboratory test of vacuum and surcharge preloading [J]. Rock and Soil Mechanics,2005,26(Suppl):95-98(in Chinese).
[7] 高志义,张美燕,刘立钰,等. 真空预压加固的离心模型试验研究[J] 港口工程,1988(1):18-24.Gao Zhiyi,Zhang Meiyan,Liu Liyu,et al. Centrifuge modeling of vacuum preloading [J]. China Harbour Engineering,1988(1):18-24(in Chinese).
[8] 林 丰,陈 环. 真空和堆载作用于砂井地基固结的边界元分析[J]. 岩土工程学报,1987,9(4):13-22.Lin Feng,Chen Huan. Analysis of consolidation of ground installed with sand drains under loading and vacuum by boundary element method [J]. Chinese Journal of Geotechnical Engineering,1987,9(4):13-22(in Chinese).
[9] 闫澍旺,孙立强,李 伟,等. 真空加固超软土工艺的室内模型试验研究[J]. 岩土工程学报,2011,33(3):341-347.Yan Shuwang,Sun Liqiang,Li Wei,et al. Model tests on vacuum preloading technology of super-soft soil [J]. Chinese Journal of Geotechnical Engineering,2011,33(3):341-347(in Chinese).
[10] 南京水利科学研究院. SL237—1999 土工试验规程[S]. 北京:中国水利水电出版社,1999.Nanjing Hydraulic Research Institute. SL237—1999 Specification of Soil Test[S]. Beijing:China Water Power Press,1999(in Chinese).
[11] Bo M W. Compressibility of Ultra-Soft Soil[M]. Singapore:World Scientific Publishing Co Ltd,2008.
(责任编辑:樊素英)
Laboratory Tests on Consolidation of Dredger Fill Under Vacuum Load
Qiu Changlin,Niu Fei,Yan Shuwang,Ji Yucheng
(School of Civil Engineering,Tianjin University,Tianjin 300072,China)
In order to study the consolidation and stress-strain relationship of dredger fill under vacuum load,a test device is designed. In this device,dredger fill consolidates as an element. The consolidation of dredger fill is studied by measuring both its volume and vertical strains under different vacuum loads. Test results show that both the vacuum loading and the deformation of dredger fill are isotropic. Volume and axial strain are in a hyperbola relationship with vacuum load. The relationship between void ratio and the logarithm of vacuum pressure is linear,which is independent of initial water content. The consolidation time and deformation under different vacuum loads show that the consolidation in the initial stage is the dominant part in the whole consolidation process. The test results can be used to construct the stress-strain relationship and predict the settlement of dredger fill under vacuum load.
vacuum load;dredger fill;consolidation;stress-strain relationship;laboratory test
TU447
A
0493-2137(2014)06-0498-06
10.11784/tdxbz201209024
2012-09-09;
2012-12-04.
天津市自然科学基金重点资助项目(11JCZDJC23900).
邱长林(1973— ),男,博士,副教授.
邱长林,qiu_cl@tju.edu.cn.
