结合高斯回归模型和隐马尔可夫随机场的模糊聚类图像分割
2014-06-02赵雪梅赵泉华
赵雪梅 李 玉 赵泉华
结合高斯回归模型和隐马尔可夫随机场的模糊聚类图像分割
赵雪梅 李 玉 赵泉华*
(辽宁工程技术大学测绘与地理科学学院遥感科学与应用研究院 阜新 123000)
为了克服经典模糊聚类图像分割算法对图像噪声的敏感性,该文提出结合高斯回归模型(GRM)和隐马尔科夫随机场(HMRF)的模糊聚类图像分割算法。该算法用信息熵正则化模糊C均值(FCM)的目标函数,再用KL(Kullback-Leibler)信息加以改进,并将HMRF和GRM模型应用到该目标函数中,其中HMRF模型通过先验概率建立标号场邻域关系,而GRM模型则在中心像素标号与其邻域像素标号一致的基础上建立特征场邻域关系。利用提出的算法和其它经典算法分别对模拟图像、真实SAR图像以及纹理图像进行了分割实验,并对分割结果进行精度评价。实验结果表明,该文提出的算法具有更高的分割精度。
图像处理;图像分割;模糊聚类;隐马尔可夫随机场;高斯回归模型;KL(Kullback-Leibler)信息
1 引言

为了在FCM图像分割算法中加入邻域像素作用,文献[5]提出约束模糊C均值(Fuzzy Clustering with Constraints, FCM_S)算法。由于该算法引入了邻域像素作用,从而在一定程度上提高了算法精度,降低噪声敏感性,但是每次迭代都要对邻域像素进行重复计算,导致算法运行较慢。文献[6]针对FCM_S算法重复计算问题,提出了改进的FCM_ S1和FCM_S2两种算法。这两种算法首先对图像进行均值或中值滤波,再利用FCM算法对滤波图像进行模糊聚类分割。为了加速FCM算法的运行速度,文献[7]提出增强模糊C均值(Enhanced Fuzzy C-Means Clustering, EnFCM) 算法。该算法首先生成一个与邻域像素有关的线性加权图像,并将目标函数直接定义在灰度级上。由于灰度级数远小于图像像素个数,从而实现了算法加速。在空间上,不同方向的邻域像素与中心像素有不同方位关系和空间距离,但前述算法没有考虑由此引起的邻域像素对分割结果的影响,且用欧氏距离定义非相似性测度对噪声和异常值敏感。因此,文献[8]定义一个与空间位置信息、邻域信息和图像强度信息有关的非相似性测度,并用该非相似性测度作为权值对原图像进行加权平均处理,从而得到一个新的线性加权图像,然后利用该图像进行迭代计算,进而提出快速广义模糊C均值(Fast Generalized Fuzzy C-Means Clustering, FGFCM)算法。但该算法需要引入两个表示空间信息和邻域信息权重的参数,而这些参数需人工选取。为了克服人工选取参数困难以及生成图像丢失原图像细节信息的问题,文献[9]提出了模糊局部信息C均值(Fuzzy Local Information C-Means Clustering, FLICM)算法。该算法定义一个包含空间信息和邻域信息的变量以控制图像噪声和细节平衡,无需人为选择参数,且仍旧利用原图像进行迭代计算,故而能得到较为满意的结果。针对FCM算法中模糊因子没有明确物理解释这一问题,用信息熵正则化FCM算法的目标函数,可以得到一种基于熵的模糊C均值(Entropy Fuzzy C-Means, EFCM)算法。文献[10]在EFCM算法基础上引入KL(Kullback-Lerbler)信息[11],并利用隐马尔科夫随机场[12](Hidden Markov Random Field, HMRF)模型刻画标号场邻域关系,提出了隐马尔科夫随机场模糊C均值(Hidden Markov Random Field-Fuzzy C-Means, HMRF-FCM)算法,并取得了较好的分割结果。
但是HMRF-FCM[10]只考虑标号场邻域关系而没有考虑特征场邻域关系。该文在HMRF-FCM算法基础上,提出同时考虑标号场和特征场邻域关系,结合高斯回归模型(Gaussian Regression Model, GRM)和HMRF模型的模糊聚类图像分割算法。其中HMRF模型通过先验概率建立标号场邻域关系,而GRM模型在中心像素标号与邻域像素标号一致的条件下建立特征场邻域关系。
2 算法描述
明晰分割方法中每个像素只能属于某一类别,而模糊分割方法中每个像素可以属于所有类别,并用模糊隶属度表示像素隶属于不同类别的程度。这种模糊分割方法需要定义像素点与聚类中心的非相似性测度,并利用该模糊隶属度和非相似性测度建立目标函数,而后通过最小化目标函数实现图像分割。在FCM算法[1]中,目标函数被定义为


式(2)中第2项是正则化项,表示分割结果的混乱程度,其系数为模糊因子,表示算法的模糊程度。
在EFCM的基础上引入KL信息[10]和HMRF[12]模型,得到HMRF-EFCM算法,目标函数可改写成
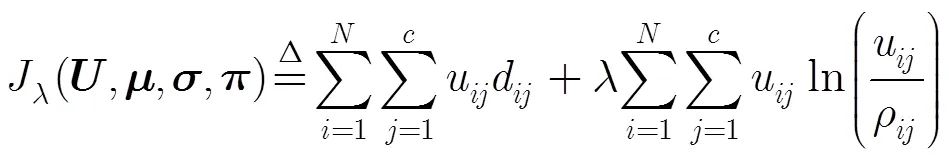
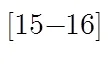




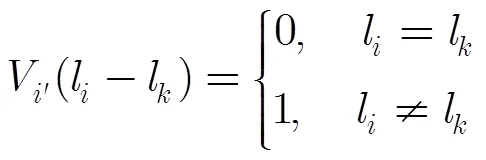
式(7)定义的先验概率在标号场中引入了邻域像素作用,由于邻域像素作用增强了标号场邻域像素标号与中心像素标号之间的作用强度,因而在一定程度上提高了算法的分割精度。

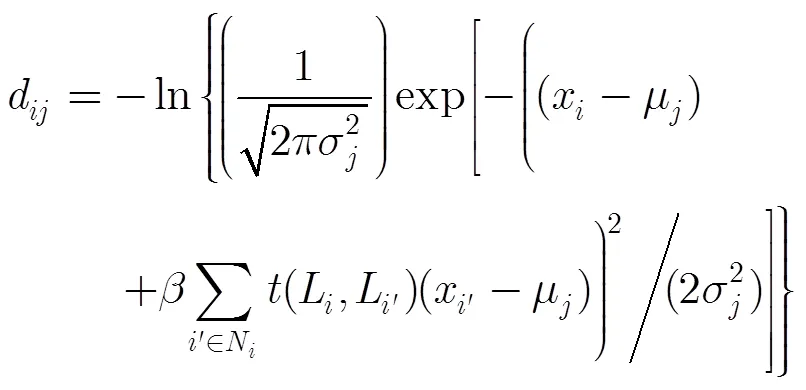


由式(9)~式(12)可以看出,特征场邻域关系不止体现在非相似性测度上,还可以对期望、方差和隶属度产生影响;而标号场邻域关系亦会影响先验概率和隶属度。可见结合特征场邻域关系和标号场邻域关系能极大程度地提高图像分割精度。综上所述,提出的算法可总结如下:
步骤1 设置循环指示器= 0、聚类数、模糊因子和迭代停止条件参数;
模糊分割与明晰分割的区别在于,前者用模糊隶属度表征像素的类属性,而后者使像素明确属于某一目标类。为了得到明晰的分割结果,要将模糊隶属度矩阵反模糊化。该文采用最大隶属度准则实现反模糊化:

3 实验和结果
3.1 模拟图像分割
为了对提出的算法进行定量评价,生成具有5个正态分布的同质区域且其分布参数已知的模拟图像。表1列出各同质区域的分布参数。图1(a)为生成模拟图像的同质区域模板,图1(b)为生成的模拟图像。
图2(a)~图2(f)分别是FCM[1], FCM_S[5], EnFCM[7], FGFCM[8], FLICM[9]以及HMRF-FCM[10]6种算法的分割结果,图2(g)是本文提出算法的分割结果。如图2(a)所示,FCM算法分割结果中有大量误分像素,这是因为FCM算法只考虑像素本身对分割的影响,因而对图像噪声和异常值敏感。FCM_S算法中加入了邻域作用,在一定程度上改善了分割结果(如图2(b))。由图2(c)-图2(d)可以看出,EnFCM和FGFCM不能有效分割区域Ⅱ和Ⅳ,这是因为二者均是FCM算法的加速算法,用生成的线性加权图像代替原图像,丢失了原图像中的细节信息。FGFCM分割结果略优于EnFCM,因为FGFCM引入了空间关系,增强了算法抗噪性。FLICM通过一个可自动获取的模糊系数控制噪声和图像细节间的平衡,提高了算法的自适应性。本例中得到的模糊系数更有利于控制噪声而忽略了对图像细节信息的保护,从而造成边缘模糊现象(如图2(e))。HMRF-FCM引入HMRF模型,建立标号场之间的邻域关系,对噪声有很好的适应性,但是没有考虑特征场邻域关系,造成区域Ⅳ和Ⅴ难以辨识 (如图2(f))。FCM算法及其改进算法没有考虑像素空间分布问题,在两个分布曲线重合的区域内,不能有效区分像素所属类别。从图2(g)结果可以看出,由于提出的算法同时考虑了标号场邻域关系和特征场邻域关系,因此在分割过程中能较好地抑制噪声,提高抗燥性,并能将各个同质区域较好的分割开。实验结果表明,同质区域内的方差对分割结果有较大的影响。由于区域Ⅱ和区域Ⅳ有较小的方差,因此所有算法均能较好地分割该区域,而区域Ⅰ具有最大的方差,因此是5个区域中分割效果最差的。但是本文提出的算法能实现对方差较大区域的有效分割,分割结果中误分像素较少;而其它算法分割结果中有大量的误分像素(见图2(a)~图2(f)),不能实现对灰度方差较大的区域进行分割。
表1高斯分布的均值和方差

同质区域ⅠⅡⅢⅣⅤ 均值1604020080120 方差3010201020

图2 模拟图像的分割结果
为了对以上不同分割方法进行精度评价,以图1(a)所示的实际同质区域为标准,对图2(a)~图2(g)所示的分割同质区域分别生成了混淆矩阵,并据此分别计算出产品精度、用户精度、总体精度和Kappa (K)系数(见表2),其中各项指标值越高,分割精度越高。由表2可知,除FLICM算法外,其它算法的总体精度均不超过80%、K值最高为0.71, FLICM算法总体精度96.9%、K值为0.96,本文提出的算法总体精度99.3%、K值为0.99。
初始均值和方差均由初始化的隶属度矩阵计算而来,因为初始是随机生成的,故而最初的均值和方差也具有随机性。实验证明,均值和方差都能在30次到40次循环之间快速收敛到其稳态值,因此非相似性测度以及隶属度矩阵等均能在30到40次循环实现收敛。
3.2 真实SAR图像分割
利用本文提出的算法、FCM算法及其改进算法对RADARSAT-ⅡSAR图像(如图3所示)进行了分割,原始图像中较暗部分是海水,明亮部分是城镇,灰色部分是森林。通过对分割结果的比较,发现FCM算法及其改进算法的分割结果均在不同程度上受到噪声影响,不能很好地对图像进行分割。其中,FCM, FCM_S, EnFCM和FGFCM算法只能把图像中的海水部分区分开来,森林和城镇部分含有大量误分像素。而FLICM和HMRF-FCM算法能分割出成片的海水、森林和城镇,但是FLICM算法将森林中分出了许多小湖面,将城镇中的树木分割成森林。HMRF-FCM算法分割效果稍好,但是森林中划分出许多小区域的城镇。这两种算法中一种对较暗的湖水敏感,另一种对明亮的城镇敏感,分割结果均不够准确。而本文提出的算法,可以较好地区分森林中小湖面和城镇边缘树木,对噪声不敏感,较好保留了图像的细节信息,保证了分割结果的准确性。

表2 算法精度(%)及Kappa(K)值比较
3.3 纹理图像分割
利用本文提出的算法和其它算法对真实纹理图像进行了分割,如图4所示。不难看出,其它算法不能很好抑制分割噪声。FLICM算法中提出的模糊系数能很好地平衡细节和噪声之间的关系,分割结果较好。HMRF-FCM算法虽然引入统计分布对分割结果的影响,但只考虑标号场邻域关系,没有考虑特征场邻域关系,只能对部分区域分割结果较好。本文算法通过GRM模型引入标号场邻域关系,使分割结果更加稳定、可靠。
4 结束语
本文在FCM算法及其改进算法的基础上,提出了一种结合HMRF和GRM模型的模糊聚类图像分割算法。该算法同时考虑标号场和特征场邻域关系,解决了经典方法分割不准确、误分像素多的问题。利用本文提出的算法、FCM算法及其改进算法分别对模拟图像、SAR图像、纹理图像进行分割实验。通过定性和定量的对比分析,表明了本文提出的算法能够克服其它算法存在大量误分像素的问题,分割结果精确,并且对不同类型图像具有较好的普适性。另外,本文提出的算法还具有收敛速度快,稳定性好的特点。

图3 真实SAR图像的分割结果

图4 真实纹理图像的分割结果
[1] Bezdek J. Pattern Recognition with Fuzzy Objective Function Algorithms[M]. New York: Plenum, 1981, 79-88.
[2] 申铉京, 何月, 张博, 等. 基于空间信息及隶属度约束的FCM图像分割算法[J]. 北京工业大学学报, 2012, 38(7): 1073-1078.
Shen Xuan-jing, He Yue, Zhang Bo,.. FCM with spatial information and membership constrains for image segmentation[J]., 2012, 38(7): 1073-1078.
[3] 陈圣国, 孙正兴, 周杰. 基于FCM和随机游走的地层图像分割方法[J]. 电子学报, 2013, 41(3): 526-531.
Chen Sheng-guo, Sun Zheng-xing, and Zhou Jie. A segmentation method for stratum image based on FCM and random walks[J]., 2013, 41(3): 526-531.
[4] 李宣平, 王雪. 模糊聚类协作区域主动轮廓模型医学图像分割[J]. 仪器仪表学报, 2013, 34(4): 860-865.
Li Xuan-ping and Wang Xue. Active contour model-based medical image segmentation method collaborative with fuzzy C-means[J]., 2013, 34(4): 860-865.
[5] Ahmed M, Yamany S, Mohamed N,.. A modified fuzzy c-means algorithm for bias field estimation and segmentation of MRI data[J]., 2002, 21(3): 193-199.
[6] Chen S and Zhang D. Robust image segmentation using FCM with spatial constraints based on new kernel-induced distance measure[J]., 2004, 34(4): 1907-1916.
[7] Szilagyi L, Benyo Z, Szilagyi S M,.. MR brain image segmentation using an enhanced fuzzy c-means algorithm[C]. Proceedings of the 25th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Cancun, Mexico, 2003, Vol.1: 724-726.
[8] Cai W, Chen S, and Zhang D. Fast and robust fuzzy c-means clustering algorithms incorporating local information for image segmentation[J]., 2007, 40(3): 825-838.
[9] Krinidis S and Chatzis V. A robust fuzzy local information c-means clustering algorithm[J]., 2010, 19(5): 1328-1337.
[10] Chatzis S P. A fuzzy clustering approach toward hidden Markov random field models for enhanced spatially constrained image segmentation[J]., 2008, 16(5): 1351-1361.
[11] Ichihashi H, Miyagishi S, and Honda K. Fuzzy c-means clustering with regularization by K-L information[C]. Proceedings of 10th IEEE International Conference on Fuzzy System, Melbourne, Australia, 2001, Vol.2: 924-927.
[12] Comer M L and Delp E J. The EM/MPM algorithm for segmentation of textured images: analysis and further experimental results[J]., 2000, 9(10): 1731-1744.
[13] 于剑, 程乾生. 关于FCM算法中的权重指数m的一点注记[J]. 电子学报, 2003, 31(3): 478-480.
Yu Jian and Cheng Qian-sheng. A note on the weighting exponent m in FCM algorithm[J]., 2003, 31(3): 478-480.
[14] Miyamoto S, Honda K, and Ichihashi H. Algorithms for Fuzzy Clustering Methods in C-Means Clustering with Applications[M]. Berlin: Springer, 2008, 47-56.
[15] Wang E. Multi-subject connectivity-based parcellation of the human IPL using Gaussian mixture models and hidden Markov random fields[C]. Proceedings of the IEEE 10th International Symposium on Biomedical Imaging, San Francisco, USA, 2013: 520-523.
[16] 朱虹, 刘薇, 姚杰, 等. 自适应阈值HMRF模型超分辨率重建[J]. 中国图象图形学报, 2012, 17(9): 1049-1054.
Zhu Hong, Liu Wei, Yao Jie.. Adaptive threshold HMRF model for super-resolution reconstruction [J]., 2012, 17(9): 1049-1054.
赵雪梅: 女,1989年生,博士生,研究方向为空间统计学、模糊数学在遥感图像处理中的应用.
李 玉: 男,1963年生,博士,教授,研究方向为遥感数据处理.
赵泉华: 女,1978年生,博士,副教授,研究方向为遥感图像建模与分析.
Image Segmentation by Fuzzy Clustering Algorithm Combining Hidden Markov Random Field and Gaussian Regression Model
Zhao Xue-mei Li Yu Zhao Quan-hua
(,,123000,)
This paper presents a new algorithm for image segmentation, which combines Hidden Markov Random Field (HMRF) and Gaussian Regression Model (GRM) to Fuzzy C-Means (FCM) clustering. The proposed algorithm uses the KL (Kullback-Leibler) information to regularize the objective function of FCM, and then utilizes HMRF and GRM to model the neighborhood relationship of the label field and feature field, respectively. The HMRF model characterizes the neighborhood relationship through its prior probability, while the GRM is established under the assumption that a pixel has the same label with its neighbors. This paper takes some experiments with the proposed algorithm and other FCM based algorithms on the simulation image, real SAR image and texture image, respectively, and the accuracy of segmentation is evaluated. By comparing the results of them, the proposed algorithm can provided more accuracy segmentation result.
Image processing; Image segmentation; Fuzzy clustering; Hidden Markov Random Field (HMRF); Gaussian Regression Model (GRM); KL (Kullback-Leibler) information
TP751
A
1009-5896(2014)11-2730-07
10.3724/SP.J.1146.2013.01751
赵泉华 zqhlby@163.com
2013-11-07收到,2014-06-05改回
国家自然科学基金(41301479),对地观测技术国家测绘地理信息局重点实验室开放基金(K201204)和辽宁工程技术大学研究生科研立项(5B2014014-01)资助课题
