Theoretical and experimental studies of the transport process of micro-particles in static water*

HAN Yi-fang (韩怡昉), MEI Ning (梅宁)

Department of Mechanical and Electronic Engineering, College of Engineering, Ocean University of China, Qingdao 266100, China, E-mail: hflora@126.com

Theoretical and experimental studies of the transport process of micro-particles in static water*

HAN Yi-fang (韩怡昉), MEI Ning (梅宁)

Department of Mechanical and Electronic Engineering, College of Engineering, Ocean University of China, Qingdao 266100, China, E-mail: hflora@126.com

(Received April 27, 2013, Revised September 27, 2013)

A theoretical model is established in this paper to investigate the micro-particle behavior in the static water. The forces acting on the micro-particles are analyzed to obtain a description of the micro-particle behavior in the static water. It is shown that the velocity of the micro-particles is a function of the diameter of the micro-particles, the density of the fluid and the micro-particles, the viscosity and the time. The micro-particleʼs motion undergoes an accelerating period and a constant velocity period, and the acceleration period of small micro-particles is very short, its velocity is much smaller than that of larger ones. The net flux of a control-volume in the flow field is calculated combined with the Fick Law. It is shown that the transport coefficient is a function of the diameter of the micro-particles, the density of the fluid and the micro-particles, the viscosity and the temperature. The transport of smaller particles is more extended than the larger ones. The digital holography technology is applied to detect the micro-particleʼs motion and the comparison between the theoretical solution and the experimental results is made, with a quantitative agreement between them.

microscale, particle, transport process, transport coefficient, digital holographic optical system

Introduction

Transport phenomenon may be seen in almost every field of chemical engineering and the transport coefficient is extensively studied in the context of the transport theory and industrial applications. Many studies were focused on the particle transport behavior and the movement characteristics by modeling, numerical simulations and experimental investigations. Generally speaking, in the theoretical aspect, the fluid mechanics theory is applied to obtain the transport coefficient. Einstein believed that[1]with the uneven distribution of the solute in a liquid along a concentration gradient direction, the transport phenomenon is due to the osmotic pressure difference. Stokes-Einstein equation shows that the transport coefficient depends on the viscosity and the temperature. Stock-Einstein equation was modified to be adapted to different systems. The Eyring theory[1]was used to calculate the net flux on a particular plane so that the transport coefficient according to the Fickʼs law can be expressed. However, the unknown parameters in this theory must be obtained by data fitting. The gas dynamics equation theory and the self-transport coefficient theory (the hard sphere model[2], the free volume theory, etc.) can be used to obtain the transport coefficient based on the intermolecular forces. In the context of the combustion theory, Qu[3]analyzed the net flux of ideal gas molecules and obtained the self-transport coefficient using a molecular transport model. It is shown that the calculation of the transport coefficient depends on the molecular mean free path and its velocity. Nie[4]studied the Brownian motion and the settlement of particles in a fluid field using the LBM. As mentioned above, the calculation of the transport coefficient depends on the velocity, which can be obtained by a stress analysis, so the core problem is the stress analysis[5]. Huang et al.[6]obtained the general formula for the discrete particleʼs motion in an arbitrary flow field by analyzing the stress with a modification.

In the field of experimental studies, Wang et al.[7]studied two phase jet flow affected by physical attri-butes of the solid phase in the gas-solid two phase flow by using the phase doppler particle analyzer (PDPA). Technology of the flow visualization and the image processing were applied in their fluid field research. Ruan[8]used tracing particles and a high-speed camera to acquire the digital images of the gas-liquid two-phase flows. The droplet diameter, the velocity and the spatial distribution of particles in the two phase flow can be obtained by the interferometric laser imaging droplet sizing (ILIDS) technique[9]and the interferometric particle imaging (IPI) technique[10]. Wang et al.[11]obtained the characteristics of the particleʼs motion of the two phase turbulent flow by using the PIV technology, the probability of the particleʼs movement near the bottom wall was also obtained. The measurement of the transport coefficient includes the membrane pool method, the optical interference method, the Taylor method, the nuclear magnetic resonance (NMR) method, and the radioactive isotope method.Through the microscope, the movement of the tracer is tracked to obtain transport parameters[12]. The technology of the digital holography as an effective observation method is widely used in the experiments of the particle transport tracking.

Although there were many studies concerning the transport coefficient, its mechanism in some cases is still not well understood. This paper studies the microparticleʼs behavior in the static water, and the effect of the diameter on the velocity and the transport coefficient, theoretically and experimentally, focusing on the spherical micro-particles in a flow field. The velocity function is obtained by the stress analysis and the net flux of a control-volume in the flow field is obtained. The transport coefficient is expressed based on the classic formula of the Fick law. Then the digital holography technology is applied to detect the microparticle motion and the comparison between the theoretical analytic solution and the experimental data sees a quantitative agreement.

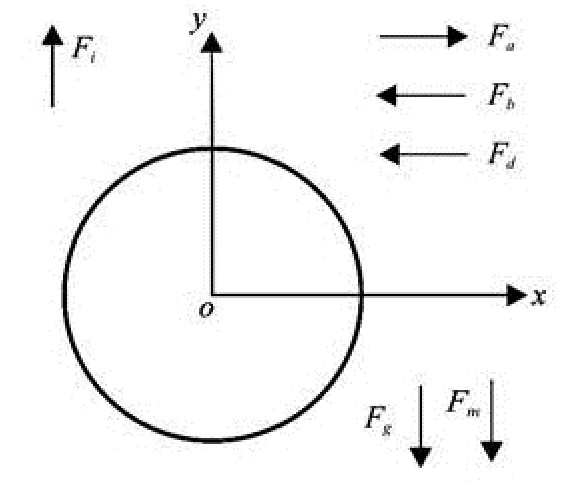
Fig.1 Stress analysis of spherical micro-particles

1. Theoretical study

1.1Physical model

In the present study, the transport behavior of the micro-particles is obtained based on its velocity, which in turn is associated with the stress. The stress mainly includes the generalized resistance (the added mass force Fa, the drag force Fdand the Basset force Fb, etc.), the generalized lift (the Magnus force Fmand the Saffman forcelF, etc.). The analysis of the main forces about the micro-particles in the fluid are shown in Fig.1.

Among all forces, in a two dimensional flow field, the spherical micro-particles are affected more significantly by the drag force, the gravity and the buoyancy, so, in this paper, only the above three forces are taken into account when the spherical microparticles move in the static water.

Based on the velocity function, the net flux of a control-volume in the two-dimensional fluid field is combined with the classic expressions of the Fick law, then the transport coefficient can be expressed in the diameter of the spherical micro-particles, the velocity, the viscosity, the density, and the temperature. In this paper, only the transport motion in the vertical direction is considered, as shown in Fig.2.

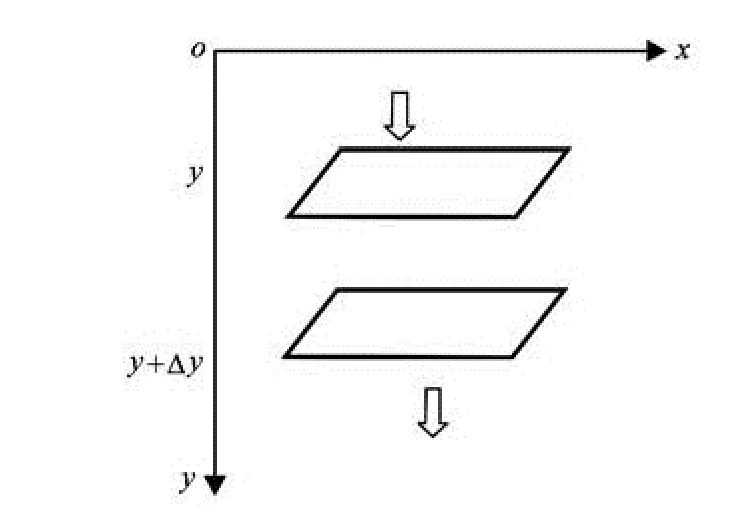
Fig.2 Motion analysis of spherical micro-particles

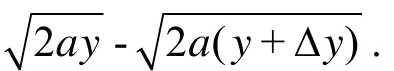
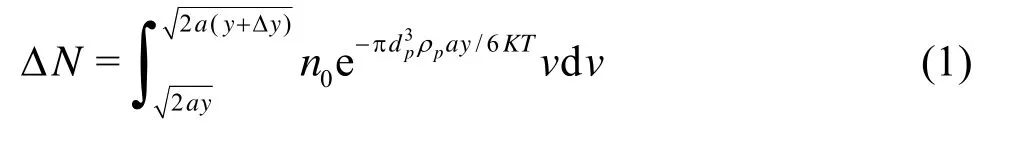
where ΔN is the net throughput, K is the Boltzmann constant, T is the Kelvins temperature, dpis the diameter of the spherical micro-particles (in this paper dpis equal to the median diameter (d50) of the diameters of the spherical micro-particles), dpis the density of the micro-particles.

1.2Theoretical model

The forces acting on the spherical micro-particles in the fluid field can be described by the Newtonʼs second law[13]

where ρfis the fluid density, vfis the fluid velocity, vpis the velocity of the spherical micro-particles, g is the acceleration of gravity, μfis the dynamic viscosity coefficient of the fluid. With the settling velocity wsand the relaxation time τpto express the dimensionless velocity and time, the dimensionless equation can be expressed as

where V is the dimensionless velocity, ζ is the dimensionless time, Resis the Reynolds number expressed with the characteristic velocity ws.

Combined with the Fick law, the net flux of the particles in a control-volume can be expressed as

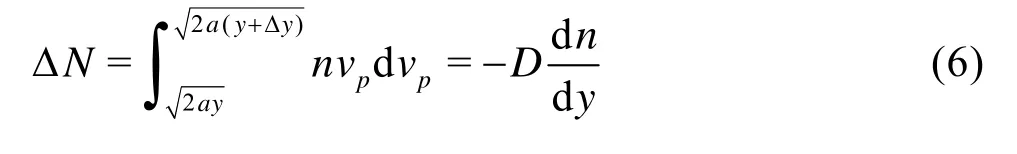
where D is the transport coefficient, a is the acceleration.

The transport efficiency is

2. The analytic solution

From Eq.(5), the dimensionless velocity (V) of the spherical micro-particles can be shown as

is the mass of the spherical micro-particles.

From the above analytic solution, the velocity of the micro-particles is a function of the diameter of the micro-particles, the densities of the fluid and the micro-particles, the viscosity and the time. The transport coefficient is a function of the diameter of the micro-particles, the density of the fluid and the microparticles, the viscosity, and the temperature.

3. Experimental study

3.1Experimental procedure

For the two-dimensional flow field, with the displacement in vertical and horizontal directions in acertain period of time, the average velocity of the spherical micro-particle in both directions can be obtained as

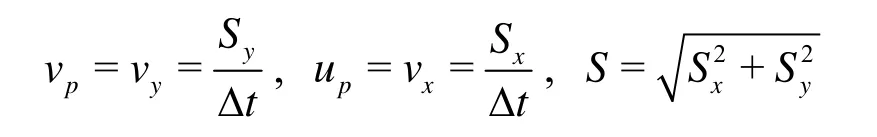
where vx, vyare the actual velocities in the horizontal and vertical directions, Sx, Syare the actual displacements in the horizontal and vertical directions, S is the total displacement.

With the holographic optical system, it is possible to describe the motion of a standard spherical micro-particle in the flow fluid[14]. And after the image and data processing using the professional software, the curves of the velocity ahainst the time can be obtained, then the theoretical results can be validated.

The holographic optical system used in this experiment is composed of the laser, the polarized light sheet, the trestle table, the experimental solution, the camera and the computer (Fig.3).

Fig.3 The holographic optical system

With the camera, the images of the micro-particles in the experimental solution irradiated by the polarized laser beam, the images of the micro-particleʼs motion within a period of time and the other experimental data (the displacements and velocities of the micro-particles) can be obtained by the professional software (the UU and Holo Prix are used to process the images, matlab is used to fit the data). After data fitting, the curves of the velocity of the micro-particles can be obtained.

In this paper, the experiments are carried out at 20oC, the measured micro-particles are the standard ones, and two groups of micro-particles with different diameters are tested in order to evaluate the effect of the micro-particle size on the results. Through the trace sampler, the aqueous solution is moved into the cuvette of 0.01 m in length, 0.011 m in width and 0.03 m in height. Then, the micro-particles with some water on their surface are put onto a flat glass plate, which is then put into a refrigerator to freeze the micro-particles onto the plate, so that a zero initial velocity of the micro-particles is achieved when the frozen micro-particles on the plate are put on the water surface of the cuvette and escape from the plate after the covered ice is melt. The ice layer is so thin that the effect of the cooled micro-particles on the aqueous solution temperature can be ignored. Also the sides and the bottom of the cuvette are covered with foam to reduce the influence of the temperature. After these preparation, turn the laser on and the images in the vertical direction, perpendicular to the laser beam can be obtained. Then the moving images of the spherical micro-particles over a certain time (it is 20 s in this paper) can be obtained after image processing.

The experimental conditions are presented in Table 1.

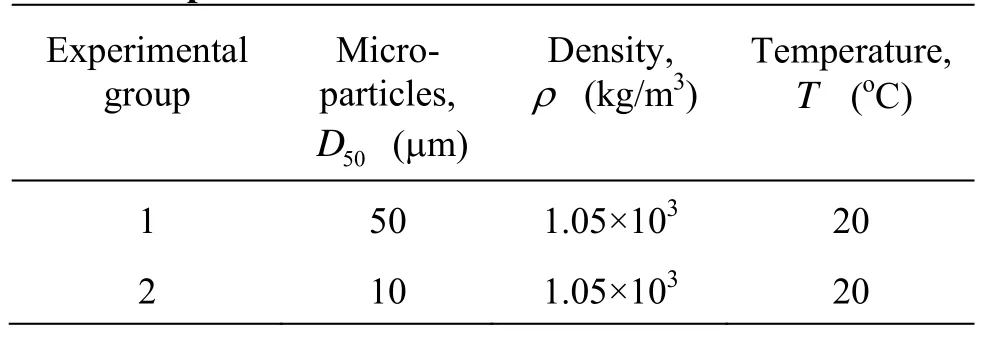
Table 1 Experiment conditions

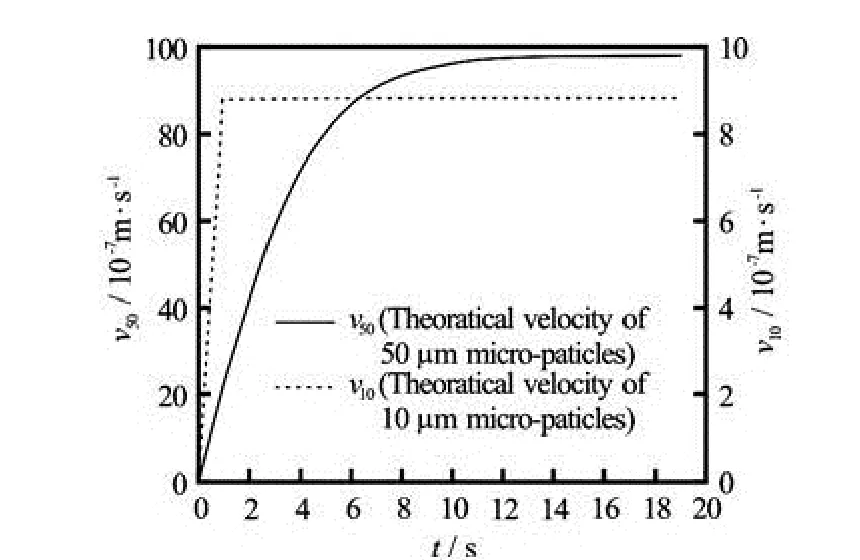
Fig.4 The curves of theoretical velocity of different diameter spherical micro-particles with time missing due

3.2Results and discussions

Fig.5 The image of spherical micro-particleʼs motions within 20 s (Notes: In the processed images, some micro-particles are to some inevitable factors in the process of experiment)

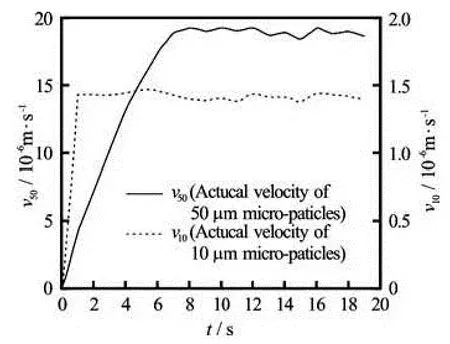
Fig.6 The curves of actual velocity of spherical micro-particles of different diameters against time (Notes: It is the statistical result of several experiments)

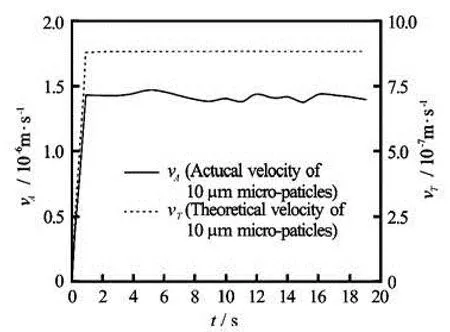
Fig.7 The curves of velocity of spherical micro-particles of 10 μm in diameter against time

The theoretical solutions of the velocity-time history for the spherical micro-particles of 50 μm in diameter and 10 μm in diameter are shown in Fig.4, where the velocity goes up with time. The images of the spherical micro-particleʼs motion in the experiment are shown in Fig.5, where the micro-particles fall down almost vertically. In the theoretical study, only three forces (the drag force, the gravity and the buoyancy) are taken into account in this paper, and it is shown that the motion of the spherical micro-particles in the static water is similar to the process of gravity sedimentation. So, only the vertical velocity is evaluated in the experiment. After the image processing and data fitting, the curves of the actual velocity of the spherical micro-particles of 50 μm and 10 μm in diameter in the static water are shown in Fig.6, where the velocity goes up with time. The comparison between the theoretical solution and the experimental results are shown in Fig.7 and Fig.8.

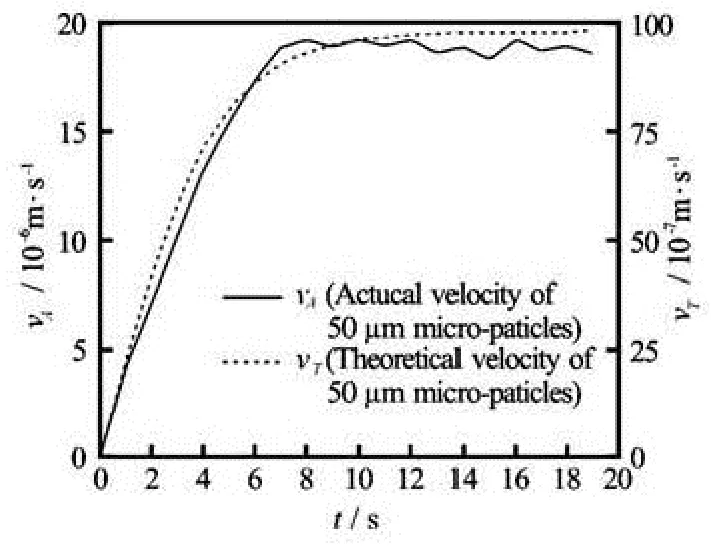
Fig.8 The curves of velocity of spherical micro-particles of 50 μm in diameter against time

In the case of the static water, the micro-particleʼs motion involves the accelerating period and the constant velocity period, and the velocity of the micro-particle is proportional to the micro-particle size. The acceleration period of the smaller micro-particles is very short, which even can be ignored as compared with the constant velocity period. The final velocity is much smaller than that of the larger ones. The explanation for this can theoretically be found in the expression of Cd, the drag coefficient, which is inversely proportional to the diameters of the micro-particles. According to Eq.(6), the velocities of the microparticles of 50 μm in diameter and 10 μm in diameter in the constant velocity period are 98.2×10-7m/s and 8.78×10-7m/s, respectively, which are close to the theoretical results from Eq.(9) in this work.

By the comparison between the theoretical solution and the experimental results, although one might say that there is a quantitative agreement, the theoretical solution is about 0.5-0.8 times the velocity of the actual results shown in Fig.7 and Fig.8. The main reasons for this are the basic assumptions about the drag force, the gravity and the buoyancy in the physical model, the other reason may be the existence of some thermophoretic force caused by the temperature difference in the aqueous solution, which can make the micro-particles move to the bottom with a lower temperature, so that, the aqueous solution around the micro-particles is also cool and moves downward along with the micro-particles, and this may also cause an increase of the micro-particleʼs downward velocity. Because of the limitation of experimental techniques, the micro-particles in the experiment are not single but in particle swarms. The micro-particles in the downward motion have an impact on their surrounded fluid which may increase the micro-particleʼsmovement, also the downward motion of a single micro-particle in any swarm may be affected by the others. Wang[15], Wu[16]obtained similar results with a difference between the actual velocity of the particles and its theoretical velocity. It is indicated that the downward motion of the particles can cause a reflux and the particles may interfere with each other in the process of motion. Nie[4]obtained a result which shows that the wake of the moving particles can bring about a smaller moving resistance and increase the velocity of their adjacent particles.

The experimental results in this paper show that there are some fluctuations in the constant velocity period of the micro-particleʼs motion. That may be due to some interference, such as the minor vibration of the test bed. Any changes of the experimental conditions may lead to the fluctuation of the micro-particleʼs motion.

The transport coefficient of the micro-particles of different diameters can be evaluated by Eq.(10), which shows that the order of magnitude for the micro-particles of 50 μm in diameter (which is about 1.9×10-19m2/s) is much smaller than that of the micro-particles of 10 μm in diameter (which is about 2×10-18m2/s). This result is supported by the conclusion of Li[17], which indicates that the transport coefficient decreases with the increase of the micro-particleʼs size. From Eq.(8) and the experimental data, the transport efficiency of the micro-particles, ε＜1.

4. Conclusions

In this work, a novel theoretical model of the micro-particleʼs transport process is established. The digital holography technology is applied to detect the micro-particleʼs motion. In addition, the influence of the micro-particles size on their motion process is analyzed. According to the comparison between the theoretical solution and the experimental results, the following conclusions can be drawn:

(1) The velocity of the micro-particles in the static water is a function of the diameter of the microparticle, the density of the fluid and the micro-particle, the viscosity and the time. The motion involves the accelerating period, with a required time to achieve the constant velocity, and the constant velocity period. The velocity is proportional to the particle size. And a coefficient =0.5-0.8

C should be required to obtain the actual velocity.

(2) The transport coefficient of the micro-particles in the static water is a function of the diameter of the micro-particle, the density of the fluid and the micro-particle, the viscosity and the temperature. The transport coefficient of the micro-particles in the static water is inversely proportional to the micro-particle size, the transport of smaller micro-particles is much more significant. And as the distribution of the microparticles tends to lead to a constant velocity, the transport coefficient tends to be zero, the main motion of the micro-particles is mainly the the settlement movement.

There are some factors that cannot be ignored, such as the temperature, the velocity of the flow, etc.. As far the research methods and studies in this work are concerned, further researches are necessary.

[1] BRUSTEIN R., MEDVED A. J. M. The shear diffusion coefficient for generalized theories of gravity[J]. Physics Letters B, 2009, 671(1): 119-122.

[2] ANA L. M., FRANCISCO A. D. S. and CARLOS M. S. New models for tracer diffusion coefficients of hard sphere and real systems: Application to gases, liquids and supercritical fluids[J]. The Journal of Supercritical Fluids, 2011, 55(3): 898-923.

[3] QU Zuo-jia, ZHANG Zhen-duo and SUN Si-cheng. Basis of combustion theory[M]. Beijing, China: National Defence Industry Press, 1988, 46-47(in Chinese).

[4] NIE De-ming. Research on the particles sedimentation and Brownian motion[D]. Doctoral Thesis, Hangzhou, China: ZheJiang University, 2011(in Chinese).

[5] MENG Xiao-gang, NI Jin-ren. Analysis on forces acting on particles in solid-liquid two-phase flows and their effects on sediment vertical sorting[J]. Journal of Hydraulic Engineering, 2002, (9): 6-13.

[6] HUANG She-hua, LI Wei and CHENG Liang-jun. On equation of discrete solid particlesʼmotion in arbitrary flow field and its properties[J]. Applied mathematics and Mechanics: English Edition, 2000, 21(3): 265-275.

[7] WANG Bing, LIU Yi and WANG Xi-lin. Experiments on turbulence modulation caused by particles with different material density in two-phase round turbulent jet[J]. Acta Aeronautica Et Astronautica Sinica, 2009, 30(10): 1829-1833.

[8] RUAN Xiao-dong, LIU Zhi-hao and QU Jian-wu. Study on application of PIV technique in two-phase flow measurement[J]. Journal of Zhejiang University: Engineering Science, 2005, 39(6): 785-788.

[9] QUEREL A., LEMAITRE P. and BRUNEL M. et al. Real-time global interferometric laser imaging for the droplet sizing (ILIDS) algorithm for airborne research[J]. Measurement Science and Technology, 2010, 21(1): 15306-15314.

[10] DAMASCHKE N., NOBACH H. and TROPEA C. Optical limits of particle concentration for multi-dimensional particle sizing techniques in fluid mechanics[J]. Experiments in Fluids, 2002, 32(2): 143-152.

[11] WANG Han-feng, LI Jing and LIU Hui-zhao et al. Experimental investigation on the particle behavior of gasparticle two phase turbulent flow in a horizontal channel using PIV[J]. Journal of Experiments in Fluid Mechanics, 2012, 26(3): 38-44.

[12] XU W., JERICHO M. H. and KREUZER H. J. Tracking particles in four dimentions with in-line holographic microscopy[J]. Optics Letters, 2003, 28(3): 164-166.

[13] MOROZOV A. N., SKRIPKIN A. V. Spherical particle Brownian motion in viscous medium as non-Markovian random process[J]. Physics Letters A, 2011, 375(46):4113-4115.

[14] STELLMACHER M., OBERMAYER K. A new particle tracking algorithm based on deterministic annealing and alternative distance measures[J]. Experiments in Fluids, 2000, 28(6): 506-518.

[15] WANG Dian-chang, YU Ming-zhong and WANG Kuixing. Experimental study on the particle motion in open channel flow[J]. Journal of Basic Science and Engineering, 2000, 8(3): 301-309.

[16] WU Ning, ZHANG Qi and QU Zhan-qing. Evaluation on calculation methods of sold particles settling velocity in fluid[J]. Oil Drilling and Production Technology, 2002, 22(2): 51-56.

[17] LI Hong, XU Wei-lin and LI Ke-feng et al. Particle diffusion coefficient calculation formula of shear turbulence in open channel[J]. Journal of Hydraulic Engineering, 2002, (8): 47-52.

10.1016/S1001-6058(14)60096-2

* Project supported by the National Natural Science Foundation of China (Grant No. 51276174).

Biography: HAN Yi-fang (1987-), Female, Ph. D. Candidate

MEI Ning, E-mail: nmei@ouc.edu.cn