Non-spherical multi-oscillations of a bubble in a compressible liquid*

WANG Qian-xi

School of Mathematics, University of Birmingham, Birmingham B15 2TT, UK, E-mail: q.x.wang@bham.ac.uk

YANG Yuan-xiang

Maritime Research Centre, School of Civil and Environmental Engineering, Nanyang Technological University, Singapore 639798, Singapore

TAN Danielle Sweimann

Department of Mechanical Engineering, National University of Singapore, Singapore 117575, Singapore

SU Jian

Nuclear Engineering Program, COPPE, Universidade Federal do Rio de Janeiro, CP 68509, Rio de Janeiro, 21941-972, Brazil

TAN Soon Keat

Nanyang Environment and Water Research Institute, Nanyang Technological University, Singapore 637142, Singapore

Non-spherical multi-oscillations of a bubble in a compressible liquid*

WANG Qian-xi

School of Mathematics, University of Birmingham, Birmingham B15 2TT, UK, E-mail: q.x.wang@bham.ac.uk

YANG Yuan-xiang

Maritime Research Centre, School of Civil and Environmental Engineering, Nanyang Technological University, Singapore 639798, Singapore

TAN Danielle Sweimann

Department of Mechanical Engineering, National University of Singapore, Singapore 117575, Singapore

SU Jian

Nuclear Engineering Program, COPPE, Universidade Federal do Rio de Janeiro, CP 68509, Rio de Janeiro, 21941-972, Brazil

TAN Soon Keat

Nanyang Environment and Water Research Institute, Nanyang Technological University, Singapore 637142, Singapore

(Received November 30, 2014, Revised December 13, 2014)

Bubble dynamics are associated with wide and important applications in cavitation erosion in many industrial systems, medical ultrasonics and underwater explosions. Two recent developments to this classical problem are reviewed in this paper. Firstly, computational studies on the problem have commonly been based on an incompressible fluid model. However, a bubble usually undergoes significantly damped oscillation due to the compressible effects. We model this phenomenon using weakly compressible theory and a modified boundary integral method. This model considers the energy loss due to shock waves emitted at minimum bubble volumes. Secondly, the computational studies so far have largely been concerned with the first-cycle of oscillation. However, a bubble usually oscillates for a few cycles before it breaks into much smaller ones. We model both the first- and second-cycles of oscillationand predict damped oscillations. Our computations correlate well with the experimental data.

compressible bubble dynamics, weakly compressible theory, boundary integral method

Introduction

Bubble dynamics is a classical problem. Traditional research into this topic has generally been associated with the mechanism of cavitation erosion in many industrial systems, such as ship propellers, turbines, pipelines and cryogenic pumps[1-7]. These continue to remain important application areas and the challenge still stands, since cavitation erosion still presents a problem and its mechanism has not been fully elucidated[8].

Recent research on bubble dynamics is associated with important medical applications, including extracorporeal shock wave lithotripsy[9-11], tissue ablating (histotripsy)[12,13], and oncology and cardiology[14]. Erosion mechanisms of cavitation are widely utilised in ultrasound cavitation cleaning-one of the most effective cleaning processes for electrical and medical micro-devices[15].

Bubble dynamics is associated with shock waves at the start, subsequent growth and collapse of the bubble, and a high-speed liquid jet.The shock wave propagates at a much smaller time scale than the bubble oscillation, so the two phenomena are usually modelled separately. The shock wave is modelled using a compressible model and the bubble dynamics are largely modelled using an incompressible model.

The inviscid model based on the boundary integral method (BIM) is grid-free in the flow domain and has been widely used in bubble boundary interactionsfor axisymmetric cases[16-26]and for three-dimensional configurations[27-36]. Bubble dynamics have also been simulated using domain approaches coupled with various interface-capturing schemes based on the Euler equation or Navier-Stokes equations[37-51].

The separated modelling of the shock wave and bubble dynamics works only before the end of the collapse phase, when shock waves are often generated again by strong compression of the bubble content and/or jet impact. A significant part of the energy of the bubble system will be lost due to the generation and propagation of shock waves. As a result, the maximum volume and oscillation period of the bubble are reduced significantly from the first-cycle of oscillation to the second-cycle[52,53]. A compressible model has to be used to simulate both the shock wave and bubble dynamics at the end of collapse.

The radial dynamics of spherical bubbles in compressible fluids have been studied extensively for many decades[54,55]. References [56] and [57] modeled spherical bubble dynamics in a compressible liquid by using matched asymptotic expansions. They proved the well-known Herring equation. Refserences [58-60] employed the doubly asymptotic approximations for spherical bubble dynamics for both the external liquid and the internal gas.

We will model this phenomenon based on a weakly compressible theory[61,62], because the associated liquid flow is often associated with a low Mach number. It has been confirmed from many experiments in the literature that the maximum velocity of a boundary-induced bubble jet is lower than 200 m/s at normal ambient pressure[53].

We will study the multi-oscillations of bubble dynamics since in reality the oscillation usually takes at least a few cycles before the bubble breaks down into much smaller ones. Our compressible model predicts the energy loss associated with the generation and propagation of shock waves at the end of collapse. The computational results of the bubble shapes correlate well with experimental data up to the end of the second oscillation.

1. Mathematical modeling

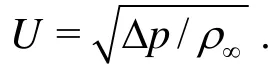
where r is the position vector, t is the time, φ is the velocity potential of the liquid and p is the pressure. The sound speed c is normalised by its value c∞in the undisturbed liquid. In the following discussion we refer to dimensionless quantities unless specified otherwise.

We introduce the bubble wall Mach number as follows,

which is assumed to be small in the present study. We assume that the flow associated with cavitation gas bubble dynamics is subsonic, more specifically, a weakly compressible flow with a low Mach number. There are strong pressure impulses as the bubble nears its minimum volume, which are characterised by an abrupt and large change in the pressure in the liquid. These strong pressure impulses are often termed as shock waves in the field of bubble dynamics.

The liquid flow at a low Mach number is governed by the equation of mass conservation,

We divide the fluid domain into two regions: the inner region near the bubble where (x, y, z) = O( Rm) and the outer region far away from the bubble where (x, y, z) = O( c∞T).

Using matched asymptotic expansions, the outer solution to second order satisfying the wave equation can be found analytically as follows, where= r /(c∞T )=εr*and m0( t*) is the negative rate of the bubble volume,

pg0*=pg0/Δp is the initial partial pressure of the non-condensable gas content of the bubble, V*is the bubble volume and V0*is its initial value, and λ is the ratio of the specific heats of the gas content, ∇*·n provides the surface curvature and σ*= σ/ (RmΔ p) is the surface tension coefficient. We assumed in Eq.(7) that the expansion and contraction of the bubble gas is adiabatic.

The far field boundary condition of the inner solution is obtained by matching the outer solution as follows

where γ is the dimensionless standoff distance of the bubble from the boundary, defined a γ =s/ Rm.

The initial boundary condition on the spherical bubble is given as follows,

Examining the initial and boundary problem of (6), one can see that the compressible effects appear only in the far field condition (8a).

2. Numerical modelling

To solve the initial boundary problem (6 and 8) using the usual boundary integral method[63], we make the following decomposition

Because Φ satisfies Laplaceʼs Eq.(10a), its solution may be represented in terms of a boundary integral on the bubble surface S when the flow domain is in a singly-connected form as follows,

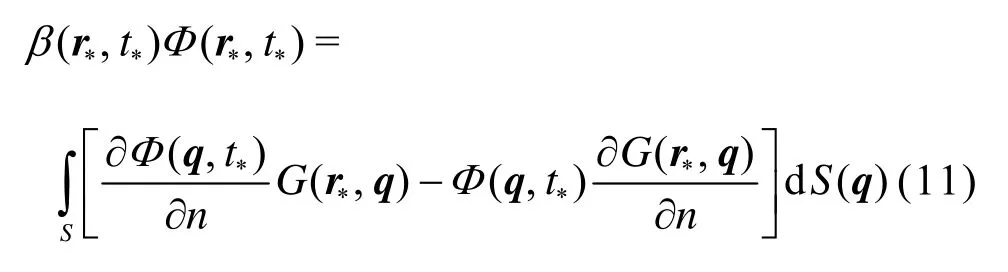
where β(r*,t*) is the solid angle at the field point r*at the time t*, under which the liquid domain is viewed from the field point r*. The solution (11) also satisfies the condition on the rigid boundary (10d) and the far field condition (10e).

At each time step, we have a known bubble surface S and a known potential distribution Φ on the bubble surface. With this information we can calculate the tangential velocity on the bubble surface. The nor-mal velocity on the bubble surface is obtained after solving the boundary integral Eq.(11). The bubble shape and the potential distribution on it can be further updated by performing the Lagrangian time integration to (10b) and (10c), respectively. The details on the numerical model using the BIM for the problem can be found in Refs.[63-65].

A high-speed liquid-jet often forms and subsequently penetrates through the bubble for non-spherical collapse. The liquid domain is then transformed from a singly-connected to a doubly-connected form, which results in non-uniqueness of the potential problem (9). The doubly-connected domain can be made singly-connected by using a vortex sheet[66,67]or a branch cut[68-70]modeled the dynamics of a bubble ring with a vortex ring inside, started with a circular crosssection. References [71,72] developed a vortex ring model from these earlier ideas to model the topological transition of a bubble and the subsequent toroidal bubble. The vortex ring model was used for modelling the toroidal bubble in this work since it avoids the treatment of the branch-cut or the vortex sheet.

3. Comparisons of computations with experiments

We carried out experiments[73]for bubble dynamics near a rigid boundary to validate the numerical model. Bubbles were generated using a focused laser pulse emitted from a Q-switched Nd, YAG laser system (LOTIS TII LS-2134UTF, wavelength 532 nm, pulse duration approximately 6 ns). Bubble evolution was recorded using an Olympus (i-SPEED 3) high-speed camera at a frame rate of 100 000 frames per second (fps), while a highpower LED flashlight (WARSUN MX900, up to 900 lumens) provided back-lighting.

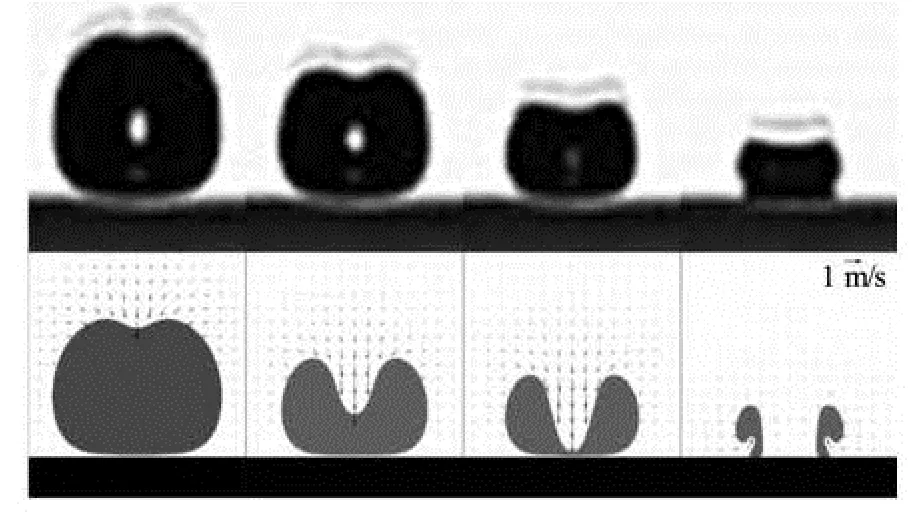
Fig.1 Comparison of the experiment (in the upper row) and the BIM computation (in the low row) for the bubble shapes for a cavitation bubble near a rigid boundary at Rm= 0.0015 m and γ=1.0, from the start of jet formation to jet impact

Figure 1 compares the computation with experiment for bubble dynamics at Rm=0.0015 m and γ =1.0, near a rigid wall (below the bubble in the figure). The bubble shapes of the experiment are shown in the upper row and the numerical results shown in the lower row, along with the velocity field of the liquid flow. They agree well until the end of the collapse phase. A liquid jet develops close to the end of collapse and the jet velocity increases with time. The maximum jet velocity calculated at the instant of impact is 81 m/s, which is within the range of experimental results from 77 m/s-114 m/s reported by Ref.[53]. After the jet impacts the opposite bubble wall, a toroidal bubble is formed as shown in the last frame of the simulation results.

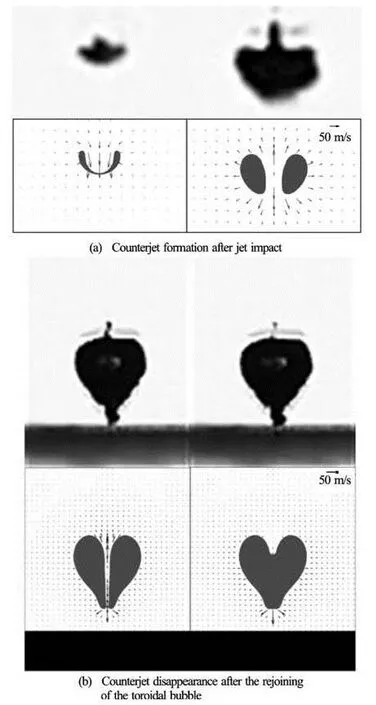
Fig.2 Comparison of the experiment (in the upper row) and the BIM computation (in the low row) for the bubble shapes for a cavitation bubble near a rigid boundary at Rm= 0.0015 m and γ=2.0

Figure 2 compares the results between the computation and experiment immediately before and afterjet impact for a cavitation bubble near a rigid boundary at Rm=0.0015 m and γ=2.0. Before jet impact, the liquid flow velocity along the axis of symmetry is directed towards the wall. However, after jet impact, a stagnation of the liquid flow forms within the jet tunnel and the velocity inside the jet tunnel exhibits two different directions. The liquid above the stagnation flows upwards, which brings along the tiny-bubbles formed at the interface between the jet and the bubble gas. This is believed to be the cause of the counterjet. In the meantime the liquid down the stagnation flows downwards,causing the formation of a liquid “tail” in the lower part of the bubble.

Figure 2(b) shows the liquid velocity fields immediately before and after the rejoining of the toroidal bubble respectively. Before rejoining, the stagnation point is associated with both up- and downward liquid flows inside the jet tunnel forming the counterjet and the bubble tail respectively. After rejoining, there is no upward liquid flow, so the counterjet starts to disappear.

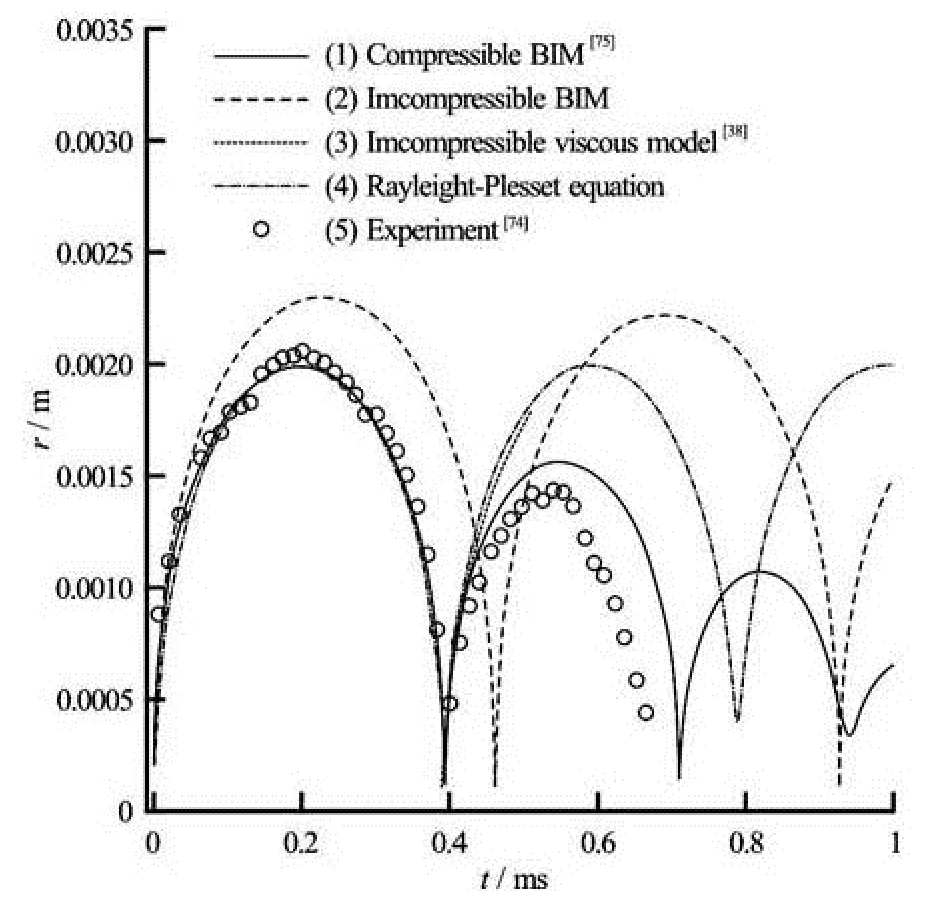
Fig.3 Comparison of the time-evolution of the bubble equivalent radius Reqfor a bubble near a rigid wall at Rm= 0.002 m, γ=2.45. The initial conditions used for (1) and (2) are R0=0.0002 m, Rt0=300 m/s and pg0= 5 MPa. The initial conditions used for (3) and (4) are R0=0.0004 m, Rt 0=0 m/s and pg0=5 MPa

Figure 3 shows a comparison of the time-evolution of the equivalent bubble radius Reqamong the compressible BIM, the incompressible BIM and the experiment[74]for a bubble near a rigid wall at Rm= 0.002 m, γ=2.45. This case was chosen as the experimental results were available, measured directly using a digital version of the photographic series and image processing techniques[38]. The initial conditions for the compressible BIM are R0=0.0002 m, Rt0= 300 m/s and pg0=5 MPa. Other parameters used for the calculation are ρ=1000 kg/m3, σ=0.07 N/m , p∞=101kPa and pv=2.98 kPa. The compressible BIM predicts significant damping of oscillation of the bubble, its maximum radius and oscillation period reduce about 25% from the first-cycle to the secondcycle of oscillation. There is about a 5% discrepancy between the results of the compressible BIM and the experiment. This may be due to the viscous effects and heat transfer neglected in the model and/or the measurement errors in the experiment.

The result for the incompressible BIM was obtained with the same initial conditions as the compressible BIM. The first maximum radius of the bubble obtained with this model is about 20% larger than the experimental value, because the acoustic radiation to the far field due to the compressible effects at the early expansion phase was neglected in this model. This discrepancy can be corrected by setting the initial conditions for an incompressible model, such as the initial conditions used for the Rayleigh-Plesset equation to be given later on. The initial conditions for the compressible model used here were to show the energy loss of a bubble system due to acoustic radiation during both the early expansion and around the end of the collapse phase, that is neglected in an incompressible model. The oscillation amplitude and period are almost the same during the first two cycles of oscillation since the compressible effects at the end of the collapse phase were neglected in the model.

The compressible effects neglected at the start of the first-cycle of oscillation can be corrected for by adjusting the initial conditions as shown in the result using the Rayleigh-Plesset equation for a spherical bubble in an infinite liquid with the initial conditions for the incompressible model: R0=0.0004 m, Rt0= 0 m/s and pg0=5.65 MPa. However the bubble undergoes undamped oscillation in the model.

Reference [38] calculated this case based on the incompressible Navier-Stokes equations with the viscosity coefficient for water chosen as 10-3kg(ms)-1. Their model predicts well the radius evolution during the first-cycle of oscillation but does not predict the significant damped oscillation observed in the experiment.

The compressible BIM successively predicts the acoustic radiation both at the beginning of the expansion phase and at the end of the collapse phase. Its agreement with the experiment indicates that the energy loss of a bubble system is primarily associated with acoustic radiation due to the compressible effects.

Fig.4 Comparison of the history of the bubble radius R for a spherical bubble starting at R0=0.0002 m , Rt0= 300 m/s and pg0=5MPa

Figure 4 compares the compressible BIM and the Keller equation for the radius history R( t) for a spherical bubble in an infinite liquid starting at R0= 0.0002 m, Rt0=300 m/s and pg0=5 MPa . The compressible BIM agrees very well with the Keller equation for more than three cycles of oscillation. This confirms that the compressible BIM predicts the compressible effects at the same level of accuracy as the Keller equation for a spherical bubble, which in fact are both valid to the first two orders of O(1) and O(ε). The small difference should be due to the numerical errors in the BIM approach as well as the higher order difference of O(ε2) between the two models. The first collapse we call the “principal collapse”is associated with the most significant energy being lost to the far field through acoustic radiation. The“principal collapse” is associated with a significant initial bubble wall velocity, a feature not present in subsequent rebounds as the bubble wall velocity is small at the beginning of rebounds[26].

4. Summary and conclusions

Bubble dynamics are associated with generation of shock waves, a liquid jet and a vortex ring. The shock wave is a pressure impulse but the associated liquid flow is usually subsonic with a small Mach number. Weakly compressible theory is thus implemented for this phenomenon using the method of matched asymptotic expansions in terms of the bubblewall Mach number. As a result, the inner flow near the bubble is described by Laplaceʼs equation with the compressible effects appearing only in the far field condition. The problem is thus modelled approximately using the boundary integral method. The toroidal bubble formed towards the end of the collapse phase is modelled using a vortex ring model. The computation traces the repeated topological changes of the bubble from a singly-connected to a doubly-connected form, and vice versa.

This theory models the energy loss due to shock waves emitted both at the beginning of expansion phase and at the end of the collapse phase. It thus predicts the significantly damped oscillation, where both the maximum bubble radius and oscillation period are reduced significantly from the first- to second-cycles of oscillation. The computational results of the bubble shapes correlate well with the experimental data to the end of the second-cycle of oscillation for a bubble initiated at various distances from the rigid boundary.

Our computations have revealed a possible mechanism for a counter-jet formed for a bubble collapsing near a rigid wall at some standoff distance. After jet impact the opposite bubble wall the jet penetrates through the bubble. A stagnation of the liquid flow may form within the jet tunnel and the liquid velocity inside the jet tunnel exhibit two different directions. The liquid on the side of the stagnation away from the wall flows away from the wall, which brings tiny-bubbles formed at the interface between the liquid jet and the bubble gas. The numerical results thus suggested that the counterjet is formed by the stagnation, the associated high pressure zone and the backflow of the liquid through the jet tunnel.

[1] RAYLEIGH L. On the pressure developed in a liquid during the collapse of a spherical cavity[J]. Philosophical Magazine Series, 1917, 34(6): 200, 94-98.

[2] TAYLOR G. I. 1942 Vertical motion of a spherical bubble and the pressure surrounding it. In underwater explosion research Volume II[M]. Washington D.C., USA: Office of Naval Research, 1950, 131-144.

[3] PLESSET M. S., PROSPERETTI A. Bubble dynamics and cavitation[J]. Annual Review Fluid Mechanics, 1977, 9: 145-185.

[4] BLAKE J. R., GIBSON D. C. Cavitation bubbles near boundaries[J]. Annual Review Fluid Mechanics, 1987, 19: 99-123.

[5] YOUNG F. R. Cavitation[M]. New York, USA: McGraw-Hill, 1989.

[6] LEIGHTON T. The acoustic bubble[M]. London, UK: Academic Press, 1994.

[7] BRENNEN C. E. Cavitation and bubble dynamics[M]. New York, USA: Oxford University Press, 1995.

[8] LAUTERBORN W., KURZ T. Physics of bubble oscillations[J]. Reports on Progress in Physics, 2010, 73(10): 106501.

[9] KLASEBOER E., FONG S. W. and TURANGAN C. K. et al. Interaction of lithotripter shockwaves with single inertial cavitation[J]. Journal of Fluid Mechanics, 2007, 593: 33-56.

[10] ILORETA J. I., FUNG N. M. and SZERI A. J. Dynamics of bubbles near a rigid surface subjected to a lithotripter shock wave: I. Consequences of interference between incident and reflected waves[J] Journal of Fluid Mechanics, 2008, 616: 43-61.

[11] CALVISI M. L., ILORETA J. I. and SZERI A. J. Dynamics of bubbles near a rigid surface subjected to a lithotripter shock wave: II. Reflected shock intensifies non-spherical cavitation collapse[J]. Journal of Fluid Mechanics, 2008, 616: 63-97.

[12] ROBERTS W. W., HALL T. L. and IVES K. et al. Pulsed cavitational ultrasound: A noninvasive technology for controlled tissue ablation (histotripsy) in the rabbit kidney[J]. Journal of Urology, 2006, 175(2): 734-738.

[13] COUSSIO C. C., ROY R. A. Applications of acoustics and cavitation to non-invasive therapy and drug delivery[J]. Annual Review Fluid Mechanics, 2007, 40: 395-420.

[14] LESLIE T. A., KENNEDY J. E. High-intensity focused ultrasound principles, current uses, and potential for the future[J]. Ultrasound Quarterly, 2006, 22(4): 263-272.

[15] SONG W. D., HONG M. H. and LUK＇YANCHUK B. et al. Laser-induced cavitation bubbles for cleaning of solid surfaces[J]. Journal of Applied Physics, 2004, 95(6): 2952-2956.

[16] LENOIR M. A calculation of the parameters of the high-speed jet formed in the collapse of a bubble[J]. Journal of Applied Mechanics, Technical Physics, 1979, 20(3): 333-337.

[17] GUERRI L., LUCCA G. and PROSPERETTI A. A numerical method for the dynamics of non-spherical cavitation bubbles[C]. Proceedings of the Second International Colloquium on Drops and Bubbles. Monterey, California, USA, 1981.

[18] BLAKE J. R., TAIB B. B. and DOHERTY G. Transient cavities near boundaries. Part 1. Rigid boundary[J]. Journal of Fluid Mechanics, 1986, 170: 479-497.

[19] BLAKE J. R., GIBSON D. C. Cavitation bubbles near boundaries[J]. Annual Review Fluid Mechanics, 1987, 19: 99-123.

[20] BLAKE J. R., HOOTON M. C. and ROBINSON P. B. et al. Collapsing cavities, toroidal bubbles and jet impact[J]. Philosophical Transactions of the Royal Society, 1997, 355: 537-550.

[21] BRUJAN E. A., KEEN G. S. and VOGEL A. et al. The final stage of the collapse of a cavitation bubble close to a rigid boundary[J]. Physics of Fluids, 2002, 14(1): 85-92.

[22] SZERI A. J., STOREY B. D. and PEARSON A. et al. Heat and mass transfer during the violent collapse of non-spherical bubbles[J]. Physics of Fluids, 2003, 15(9): 2576-2586.

[23] PEARSON A., BLAKE J. R. and OTTO S. R. Jets in bubbles[J]. Journal of Engineering Mathematics, 2004, 48(3-4): 391-412.

[24] LIND S. J., PHILLIPS T. N. The influence of viscoelasticity on the collapse of cavitation bubbles near a rigid boundary[J]. Theoretical and Computational Fluid Dynamics, 2012, 26(1-4): 245-277.

[25] CURTISS G. A., LEPPINEN D. M. and WANG Q. X. et al. Ultrasonic cavitation near a tissue layer[J]. Journal of Fluid Mechanics, 2013, 730: 245-272.

[26] WANG Q. X. Underwater explosion bubble dynamics in a compressible liquid[J]. Physics of Fluids, 2013, 25(7): 072104.

[27] CHAHINE G. L., BOVIS A. Oscillation and collapse of a cavitation bubble in the vicinity of a two-liquid interface. Cavitation and inhomogeneities in underwater acoustics[M]. New York, USA: Springer-Verlag, 1980.

[28] CHAHINE G. L., PERDUE T. O. Simulation of the three-dimensional behaviour of an unsteady large bubble near a structure[C]. Proceedings of the Third International Colloquium on Drops and Bubbles. Monterey, California, USA, 1988.

[29] CHAHINE G. L., HARRIS G. Multi-cycle underwater explosion bubble model. Part I: Theory and validation examples for free-field bubble problems[R]. U.S. Naval Surface Warfare Center Indian Head Division, Report IHCR 98-64, 1998.

[30] CHAHINE G. L., HARRIS G. Multi-cycle underwater explosion model. Part II: Validation examples for hull girder whipping problems[R]. U.S. Naval Surface Warfare Center Indian Head Division, Report IHCR 98-65, 1998.

[31] DUNCAN J. H., MILLIGAN C. D. and ZHANG S. G. On the interaction between a bubble and a submerged compliant structure[J]. Journal of Sound and Vibration, 1996, 197(1): 17-44.

[32] WANG Q. X. The evolution of a gas bubble near an inclined wall[J]. Theoretical and computational fluid dynamics, 1998, 12: 29-51.

[33] WANG Q. X. The numerical analyses of the evolution of a gas bubble near an inclined wall[J]. Physics of Fluids, 2004, 16: 1610-1619.

[34] KLASEBOER E., HUNG K. C. and WANG C. et al. Experimental and numerical investigation of the dynamics of an underwater explosion bubble near a resilient/rigid structure[J]. Journal of Fluid Mechanics, 2005, 537: 387-413.

[35] JAYAPRAKASH A., HSIAO Chao-Tsung, and CHAHINE G. Numerical and experimental study of the interaction of a spark-generated bubble and a vertical wall[J]. Journal of Fluids Engineering, 2010, 134: 031301.

[36] JAYAPRAKASH A., SINGH S. and CHAHINE G. Experimental and numerical investigation of single bubble dynamics in a two-phase bubbly medium[J]. Journal of Fluids Engineering, 2011, 133(12): 121305.

[37] YU P. W., CECCIO S. L. and TRYGGVASON G. The collapse of a cavitation bubble in shear flows-A numerical STUDY[J]. Physics of Fluids, 1995, 7(11): 2608-2616.

[38] POPINET S., ZALESKi S. Bubble collapse near a solid boundary: A numerical study of the influence of viscosity[J]. Journal of Fluid Mechanics, 2002, 464: 137-163.

[39] TURANGAN C. K., JAMALUDDIN A. R. and BALL G. J. et al. Free-Lagrange simulations of the expansion and jetting collapse of air bubbles in water[J]. Journal of Fluid Mechanics, 2008, 598: 1-25.

[40] MINSTER V., De WILDE J. and PROOST J. Simulation of the effect of viscosity on jet penetration into a single cavitating bubble[J]. Journal Applied Physics, 2009, 106: 084906.

[41] Jr. WARDLAW A., LUTON J. A. Fluid-structure interaction mechanisms for close-in explosions[J]. Shock and Vibration Journal, 2000, 7(5): 265-275.

[42] Jr. WARDLAW A., LUTON J. A. and RENZI J. R. et al. The Gemini Euler solver for the coupled simulation of underwater explosions[R]. NSWCIHD/IHTR, 2500, 2003.

[43] Jr. WARDLAW A., LUTON J. A. and RENZI J. R. et al. Fluid-structure coupling methodology for undersea weapons. Fluid structure interaction II[M]. Southampton, UK: WIT Press, 2003, 251-263.

[44] ADOUA R., LEGENDRE D. and MAGNAUDET J. Reversal of the lift force on an oblate bubble in a weakly viscous linear shear flow[J]. Journal of Fluid Mechanics, 2009, 628: 23-41.

[45] BONHOMME R., MAGNAUDET J. and DUVAL F. et al. Inertial dynamics of air bubbles crossing a horizontal fluid-fluid interface[J]. Journal of Fluid Mechanics, 2012, 707: 405-443.

[46] BONOMETTI T., MAGNAUDET J. An interface-capturing method for incompressible two-phase flows. Validation and application to bubble dynamics[J]. International Journal of Multiphase Flow, 2007, 33(2): 109-133.

[47] HUA J., LOU J. Numerical simulation of bubble rising in viscous liquid[J]. Journal of Computational Physics, 2007, 222: 769-795.

[48] JOHNSEN E., COLONIUS T. Shock-induced collapse of a gas bubble in shockwave lithotripsy[J]. Journal of the Acoustical Society of America, 2008, 124(4): 2011-2020.

[49] JOHNSEN E., COLONIUS T. Numerical simulation of non-spherical bubble collapse[J]. Journal of Fluid Mechanics, 2009, 629: 231-262.

[50] YUE P., FENG J. J. and BERTELO C. A. et al. An arbitrary Lagrangian-Eulerian method for simulating bubble growth in polymer foaming[J]. Journal of Computational Physics, 2007, 226: 2229-2249.

[51] YANG B., PROSPERETTI A. Vapour bubble collapse in isothermal and non-isothermal liquids[J]. Journal of Fluid Mechanics, 2008, 601: 253-279.

[52] TOMITA Y., SHIMA A. Mechanisms of impulsive pressure generation and damage pit formation by bubble collapse[J]. Journal of Fluid Mechanics, 1986, 169: 535-564.

[53] PHILIPP A., LAUTERBORN W. Cavitation erosion by single laser-produced bubbles[J]. Journal of Fluid Mechanics, 1998, 361: 75-116.

[54] HERRING C.The theory of the pulsations of the gas bubbles produced by an underwater explosion[R]. US National Defence Research Communication Report, 1941.

[55] KELLER J. B., KOLODNER I. I. Damping of underwater explosion bubble oscillations[J]. Journal of Applied Physics, 1956, 27(10): 1152-1161.

[56] PROSPERETTI A., LEZZI A. Bubble dynamics in a compressible liquid. Part. 1. First-order theory[J]. Journal of Fluid Mechanics, 1986, 168: 457-478.

[57] LEZZI A., PROSPERETTI A. Bubble dynamics in a compressible liquid. Part. 2. Second-order theory[J]. Journal of Fluid Mechanics, 1987, 185: 289-321.

[58] GEERS T. L., ZHANG P. Doubly asymptotic approximations for submerged structures with internal fluid volumes[J]. Journal Applied Mechanics, 1994, 61: 893-906.

[59] GEERS T. L., HUNTER K. S. An integrated wave-effects model for an underwater explosion bubble[J]. Journal of the Acoustical Society of America, 2002,11(1): 1584-1601.

[60] GEERS T. L., LAGUMBAY R. S. and VASILYEV O. V. Acoustic-wave effects in violent bubble collapse[J]. Journal Applied Physics, 2012, 112(5): 054910.

[61] WANG Q. X., BLAKE J. R. Non-spherical bubble dynamics in a compressible liquid. Part 1. Travelling acoustic wave[J]. Journal of Fluid Mechanics, 2010, 659: 191-224.

[62] WANG Q. X., BLAKE J. R. Non-spherical bubble dynamics in a compressible liquid. Part 2. Acoustic standing wave[J]. Journal of Fluid Mechanics, 2011, 679: 559-581.

[63] WANG Q. X., YEO K. S. and KHOO B. C. et al. Nonlinear interaction between gas bubble and free surface[J]. Computers and Fluids, 1996, 25(7): 607-628.

[64] TAIB B. B. Boundary integral method applied to cavitation bubble dynamics[D]. Doctoral Thesis, New South Wales, Australia: The University of Wollonggong, 1985.

[65] BEST J. P. The rebound of toroidal bubbles. In bubble dynamics and interface phenomena[M]. Dordrecht, The Netherlands: Kluwer, 1994, 405-412.

[66] ZHANG S. G., DUNCANAND J. H. and CHAHINE G. L. The final stage of the collapse of a cavitation bubble near a rigid wall[J]. Journal of Fluid Mechanics, 1993, 257: 147-181.

[67] ZHANG S. G., DUNCAN J. H. On the non-spherical collapse and rebound of a cavitation bubble[J]. Physics of Fluids, 1994, 6(7): 2352-2357.

[68] BEST J. P. The formation of toroidal bubbles upon collapse of transient cavities[J]. Journal of Fluid Mechanics, 1993, 251: 79-107.

[69] PEDLEY T. J. The toroidal bubble[J]. Journal of Fluid Mechanics, 1968, 32: 97-112.

[70] LUNDGREN T. S., MANSOUR N. N. Vortex ring bubbles[J]. Journal of Fluid Mechanics, 1991, 72: 391-399.

[71] WANG Q. X., YEO K. S. and KHOO B. C. et al. Strong interaction between buoyancy bubble and free surface[J]. Theoretical and Computational Fluid Dynamics, 1996, 8(1): 73-88.

[72] WANG Q. X., YEO K. S. and KHOO B. C. et al. Vortex ring modelling for toroidal bubbles[J]. Theoretical and Computational Fluid Dynamics, 2005, 19(5): 303-317.

[73] YANG Y. X., WANG Q. X. and KEAT T. S. Dynamic features of a laser-induced cavitation bubble near a solid boundary[J]. Ultrasonics Sonochemistry, 2013, 20(4): 1098-1103.

[74] LAUTERBORN W., OHL C. D. Cavitation bubble dynamics[J]. Ultrasonics Sonochemistry, 1997, 4(2): 65-75.

[75] WANG Q. X. Multi-oscillation of a bubble in a compressible liquid near a rigid boundary[J]. Journal of Fluid Mechanics, 2014, 745: 509-536.

10.1016/S1001-6058(14)60093-7

* Biography: WANG Qian-xi (1960-), Male, Ph. D.