电缆隧道中盾构接地系统接地电阻简化计算公式

杜学龙，仇天骄，张晓颖，马学良，尹凡，郭健，邹军

(1．清华大学电机系，北京100084;2．北京电力经济技术研究院，北京100055)

电缆隧道中盾构接地系统接地电阻简化计算公式

杜学龙1，仇天骄2，张晓颖2，马学良2，尹凡2，郭健2，邹军1

(1．清华大学电机系，北京100084;2．北京电力经济技术研究院，北京100055)

接地电阻是接地系统安全运行的重要参数之一。本文通过仿真验证，给出了盾构接地系统(基于盾构结构的接地系统)接地电阻的简化计算公式。简化电缆隧道中盾构接地系统，建立相应的有限元仿真模型;通过仿真研究隧道中钢筋层数、钢筋个数、水泥层电导率、水泥层厚度对接地电阻的影响;根据仿真结果将求解复杂的隧道接地系统接地电阻的问题等效为求解埋地圆柱导体接地电阻的问题，并给出埋地圆柱导体接地电阻的简化计算公式。数值计算表明，简化公式计算精度满足工程要求，可用于计算电缆隧道中盾构接地系统的接地电阻。

电缆隧道;接地系统;接地电阻

1 引言

接地电阻是电缆接地系统安全运行的重要参数之一，接地电阻的计算对接地系统设计有重要意义［1-3］。

对于采用电缆沟敷设和地下直埋的地下电缆系统，其接地系统一般是人工接地装置。近年来，随着城市供电容量增大，500kV和220kV电缆系统广泛敷设在地下隧道中，出于结构安全的考虑，地下隧道墙体均采用钢筋混凝土结构，利用混凝土中的钢筋作为接地体，可极大简化电缆系统接地装置。为方便计，称其为盾构接地系统。

盾构法是暗挖法施工中的一种全机械化施工方法，用于隧道开挖、衬砌等施工，具有安全性高、工作效率高、自动化性强等优点［4］。目前，采用盾构机和预制钢筋混凝土联合施工的工艺是地下隧道建设的方法之一。

接地电阻计算主要有两种方法，即解析计算方法和数值计算法［5-8］。对于结构简单的典型接地装置，可采用解析方法计算。对于任意布置的接地装置，考虑接地系统之间的耦合关系，需采用数值计算技术予以计算。数值方法的特点是可计算任意布置和具有复杂媒质分布的接地系统，但是，在使用中数值方法的数据输入量大，边界条件设置需要一定技巧，不便于在工程中使用。

对于本文讨论的盾构接地问题，由于盾构接地系统周围媒质多样性及钢筋网络结构复杂性，通过解析公式求解盾构接地系统接地电阻有一定的困难。

针对以上问题，本文以北京市海淀区500kV送电工程中隧道为例，先建立有限元仿真模型，分析盾构接地系统接地电阻的影响因素，根据仿真结果将复杂的盾构接地系统等效为埋地圆柱导体，并给出埋地圆柱导体接地电阻的简化计算公式。通过与数值计算结果的对比，证明本文获得的简化计算公式可满足工程计算要求。同时，公式无需复杂的数值计算过程，便于在工程中应用。

2 有限元方法求解盾构接地系统接地电阻

2.1 盾构接地系统接地电阻求解问题

海淀500kV送电工程采用架空与电缆混合线路，电缆主要敷设在直径为5.4m的圆形隧道内，如图1所示。

由图1可知，盾构接地系统主要由内外两层钢筋组成。对于外侧钢筋层，主要由沿隧道截面方向的圆形钢筋和沿隧道方向的纵向钢筋组成，其中两个圆形钢筋为一组，并通过纵向钢筋与其他圆形钢筋相连;同理，隧道内侧钢筋层有相同的结构。对于该盾构接地系统，可以将其视为等位体，便于有限元计算。

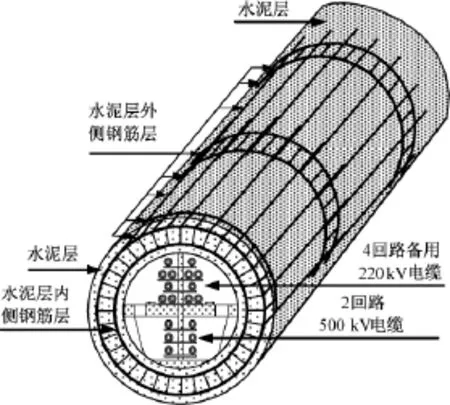
图1 圆形隧道盾构接地系统Fig．1Grounding system using tunnel foundaiton(GSTF)of circular tunnel

2.2 盾构接地系统的有限元模型

忽略盾构接地系统中横向钢筋，建立盾构接地系统二维有限元仿真模型，如图2所示。图2中d为隧道深度，r为求解区域半径，σ1为土壤电导率，σ2为隧道水泥层电导率，Ω1为土壤求解区域，Ω2为隧道水泥层求解区域。图3为盾构接地系统有限元模型中的隧道模型，r隧内为隧道内侧半径，r隧外为隧道外侧半径，r钢内为内侧钢筋层的半径，r钢外为外侧钢筋层的半径，r钢1为内侧钢筋的半径，r钢2为外侧钢筋的半径，θ1为内侧钢筋层相邻钢筋的角度，θ2为外侧钢筋层相邻钢筋的角度。

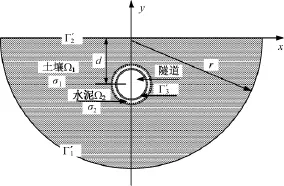
图2 圆形隧道盾构接地系统有限元模型Fig．2Finite element model of GSTF of circular tunnel

盾构接地体泄漏电流在其周围媒质中将产生地电位变化，这属于恒定电流场问题。根据图2建立以电位φ为变量的边值问题。为简化计算，令钢筋层的电位为1 V，在求解区域内，其相应的边值问题描述如下［9］:

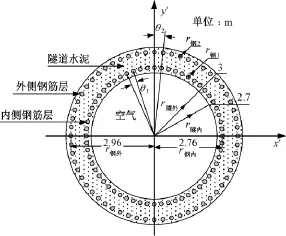
图3 圆形隧道模型Fig．3Model of circular tunnel

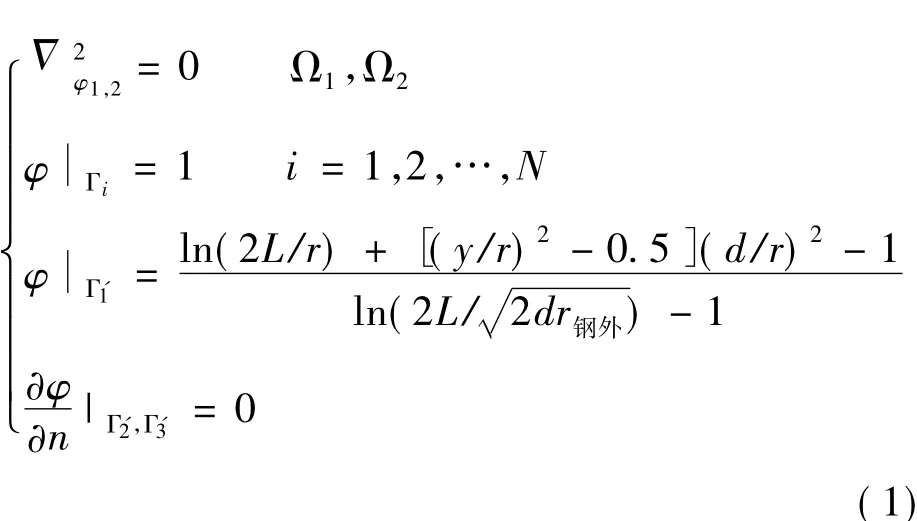
式中，N为钢筋的总数量;Γi为模型中第i根钢筋的边界;Γ'1为求解区域的半圆形边界，其边界条件推导见附录;Γ'2为地面分界面;Γ'3为隧道水泥层边界;L为隧道长度;y为图2中的坐标值;n为钢筋法向方向且由水泥指向钢筋。

根据式(1)，得隧道盾构接地系统接地电阻为:

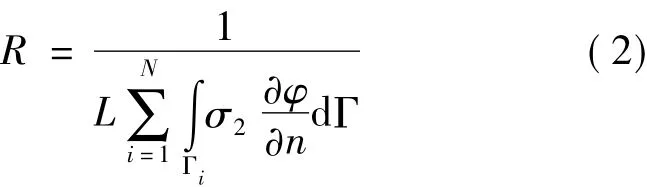
3 盾构接地系统接地电阻影响因素分析

采用2.2节建立的盾构接地系统有限元模型，分析盾构接地系统接地电阻的影响因素，具体过程如下文所述。

3.1 隧道内侧钢筋层对接地电阻的影响

选择计算参数为:r隧内=2.7m，r隧外=3m，r钢内= 2.76m，r钢外=2.96m，r钢2=5mm，r=32m，d=8m，L =6km，σ1=σ2=0.01S/m，θ2=6°，r钢1=5mm、10mm，θ1=6°～180°，即内侧钢筋个数变化范围为2～60个，同时考虑没有内侧钢筋层的情况。计算结果如图4和图5所示，其中相对误差以求内侧钢筋层相邻钢筋的角度为6°时的计算结果为基准值。

根据图4和图5可知，隧道内侧钢筋层钢筋个数对盾构接地电阻的影响较小，忽略内侧钢筋网络将有1%左右的相对误差。

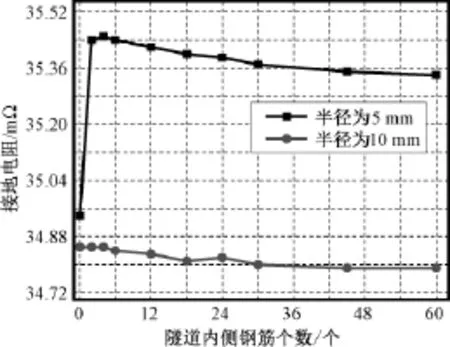
图4 隧道内侧不同钢筋个数时接地电阻Fig．4Grounding resistance with different numbers of reinforced bar inside of tunnel

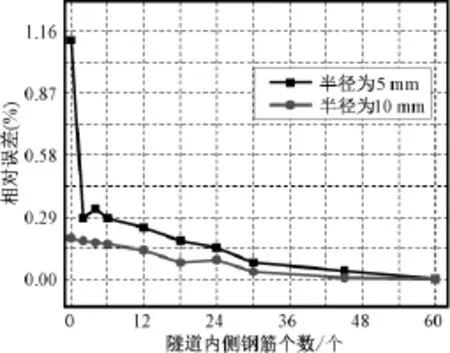
图5 隧道内侧不同钢筋个数时接地电阻相对误差Fig．5Relative difference of grounding resistance with different numbers of reinforced bar inside of tunnel

3.2 隧道外侧钢筋数量对接地电阻的影响

选择计算参数为:r隧内=2.7m，r隧外=3m，r钢外= 2.96m，r=32m，d=8m，L=6km，σ1=σ2=0.01 S/m，r钢2=5mm、10mm，θ2=3°～20°，即外侧钢筋层钢筋数量的变化范围为18～120个，忽略内侧钢筋网络。计算结果如图6和图7所示，其中相对误差以相邻钢筋角度为3°时计算结果为基准值。

根据图6和图7可知，当同层钢筋相邻角度小于6°，即钢筋个数大于60时，可以将钢筋层等效为钢壳，存在的相对误差小于2%。

3.3 隧道水泥层电导率对接地电阻的影响

选择计算参数为:r隧内=2.7m，r隧外=3m，r钢内= 2.76m，r钢外=2.96m，r钢1=r钢2=5mm，r=32m，d= 8m，L=6km，θ1=θ2=6°，σ1=0.001S/m、0.01S/m，σ2=0.001～0.1S/m。计算结果如图8～图11所示，其中相对误差以土壤电导率和水泥层电导率相等时计算结果为基准值。

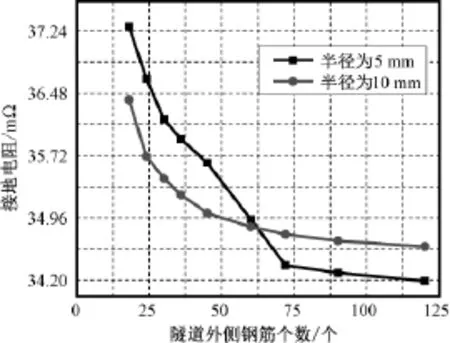
图6 隧道外侧不同钢筋个数时接地电阻Fig．6Grounding resistance with different numbers of reinforced bar outside of tunnel

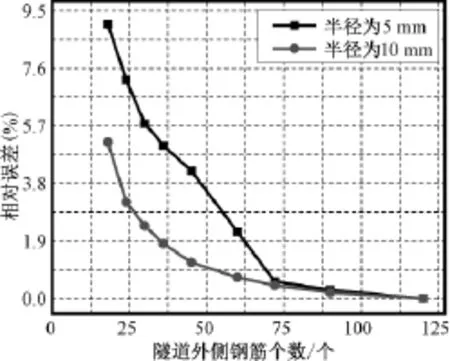
图7 隧道外侧不同钢筋个数时接地电阻相对误差Fig．7Relative difference of grounding resistance with different numbers of reinforced bar outside of tunnel

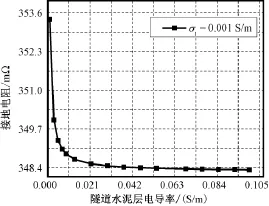
图8 σ1=0.001S/m，不同隧道水泥层电导率时接地电阻Fig．8Grounding resistance with different conductivity of cement layer，σ1=0.001S/m

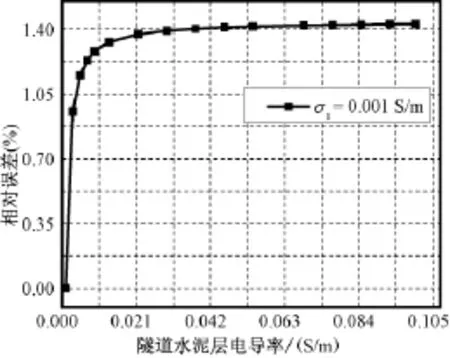
图9 σ1=0.001S/m，不同隧道水泥电导率时接地电阻相对误差Fig．9Relative difference of grounding resistance with different conductivity of cement layer，σ1=0.001S/m

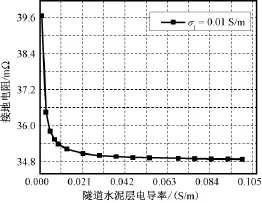
图10 σ1=0.01S/m，不同隧道水泥电导率时接地电阻Fig．10Grounding resistance with different conductivity of cement layer，σ1=0.01S/m

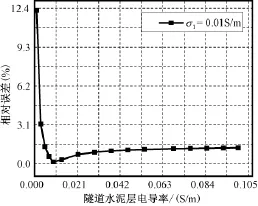
图11 σ1=0.01S/m，不同隧道水泥电导率时接地电阻相对误差Fig．11Relative difference of grounding resistance with different conductivity of cement layer，σ1=0.01S/m

根据图8～图11可知，当土壤电导率为水泥电导率3倍以下时，改变水泥电导率产生的相对误差在3%以下。

3.4 隧道水泥层厚度对接地电阻的影响

计算参数为:r隧内=2.7m，r钢内=2.76m，r钢1= r钢2=5mm，r=32m，d=8m，L=6km，σ1=0.01S/m，θ1=θ2=6°，σ2=0.005S/m、0.05S/m，r隧外=3～3.8m，r钢外=2.96～3.76m，计算结果如图12和图13所示，其中相对误差以隧道外半径为3m时计算结果为基准值。

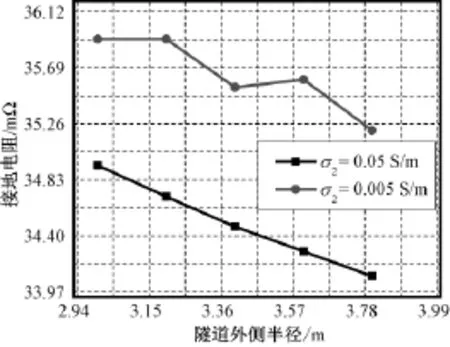
图12 不同隧道外半径时接地电阻Fig．12Grounding resistance with different radii of outside tunnel

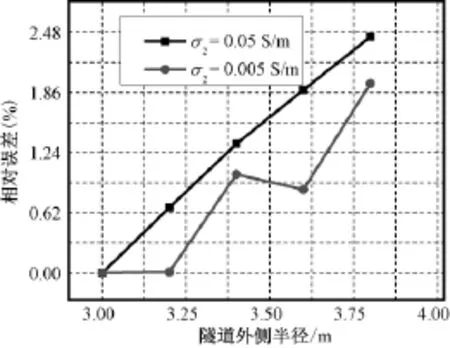
图13 不同隧道外半径时接地电阻相对误差Fig．13Relative difference of grounding resistance with different radii of outside tunnel

根据图12和图13可知，当水泥层厚度变化小于1m时，产生的相对误差小于2.5%。

4 盾构接地系统接地电阻简化计算公式

4.1 盾构接地系统接地电阻计算公式推导

通过以上分析可知，可以将圆形隧道盾构接地系统等效为埋地圆柱导体，如图14所示。该圆柱导体埋地深度与圆形隧道埋地深度相同，圆柱导体半径与圆形隧道外侧钢筋层半径相同。作埋地圆柱导体的镜像，如图14中M'N'所示，通过镜像法将土壤变为均匀媒质，其电导率为σ1。

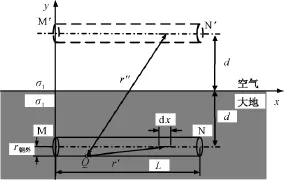
图14 埋地圆柱导体Fig．14Buried cylindrical conductor

假设泄漏电流I由圆柱体中心轴线向土壤中均匀流散，且整段导体表面的电位基本相等，可得圆柱导体表面任意一点Q的电位如式(3)所示。采用平均电位法，即将导体各点电位的平均值作为导体的电位，可得埋地圆柱导体接地电阻，如式(4)所示。若L＞＞2d＞＞2r钢外，可得埋地圆柱导体接地电阻的简化公式，如式(5)所示［10］。

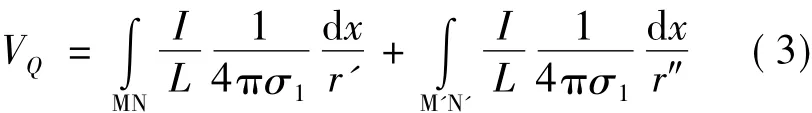
式中，r'为导体段dx到任一点Q的距离;r″为导体段dx的镜像到任一点Q的距离。

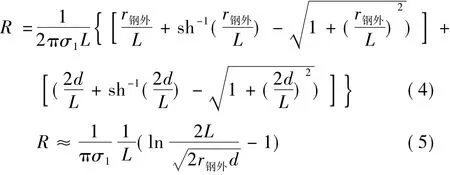
4.2 盾构接地系统接地电阻计算公式验证

采用实际盾构参数如下:r隧内=2.7m，r隧外= 3m，r钢内=2.76m，r钢外=2.96m，r钢1=r钢2=5mm，r= 32m，d=8m，L=6km，σ1=(1/120)S/m，σ2=100 S/m，θ1=θ2=6°。采用有限元仿真和简化公式计算盾构接地系统的接地电阻，计算结果分别为41.66Ω、41.15Ω，以有限元仿真计算结果为基准值，两种方法计算结果的相对误差为1.224%，由此可见简化公式计算精度较高，可以用于求解圆形隧道盾构接地系统的接地电阻。

5 结论

本文采用有限元方法分析盾构接地系统接地电阻的影响因素，给出计算圆形隧道盾构接地系统接地电阻的简化公式。计算表明，当隧道外侧钢筋层中钢筋个数大于60、土壤电导率小于3倍水泥层电导率且隧道水泥层厚度小于1m时，可将求解圆形隧道盾构接地系统接地电阻的问题等效为求解埋地圆柱导体接地电阻的问题;当隧道长度远大于2倍的隧道埋地深度且隧道埋地深度远大于隧道外侧钢筋层半径时，可采用本文简化公式计算盾构接地系统的接地电阻。

附录

当一根处于无限大均匀媒质中的圆棒电极流入媒质中电流为I1，则在距离圆棒垂直距离为a处的电压为:

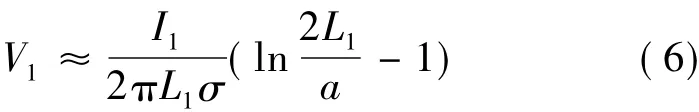
式中，L1为圆棒电极长度，且L1＞＞a，σ为均匀媒质的电导率。

图15为圆形隧道有限元模型，图中忽略水泥层，并将钢筋网络等效为钢壳，由此近似确定求解区域的边界条件。钢筋壳的长度L相对于半径r钢外可视为无限长，设通过钢壳流入大地的电流为I，通过镜像法将半无限大土壤媒质变为无限大媒质。

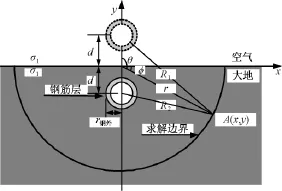
图15 圆形隧道有限元模型Fig．15Finite element model of circular tunnel

由于L＞＞2d＞＞2r钢外，根据式(6)可得钢壳上的电压近似为:

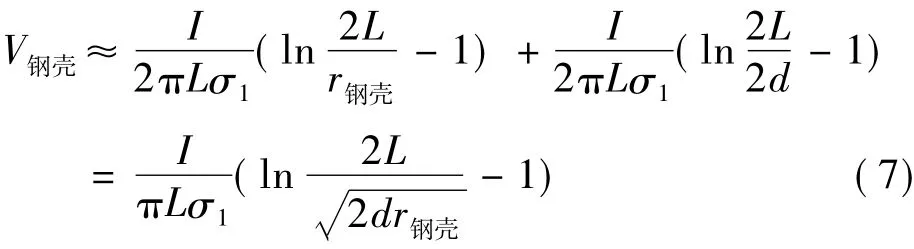
由于L＞＞R1、L＞＞R2，根据式(6)可求解边界上A点的电压近似为:

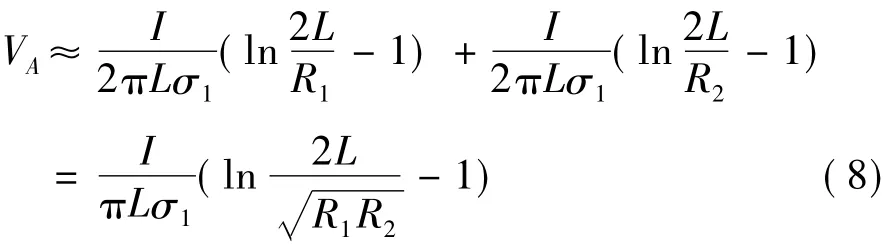
因此，在隧道钢筋接地系统有限元模型中，设定钢筋上电压为1V，则求解边界上电压近似为:

为方便边界条件的设定，对式(9)进行化简。在图15中，根据余弦定理可得:

根据式(10)和泰勒公式得:

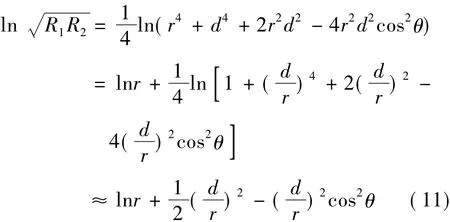
在图15中，存在:

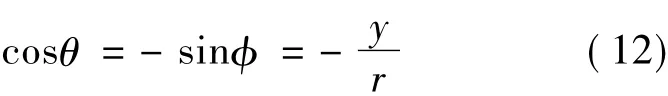
将式(11)和式(12)代入式(9)，化简得边界Γ'1上的边界条件，如式(1)所示。

［1］王斌，张宇，贲飞，等(Wang Bin，Zhang Yu，Ben Fei，el al．)．基于虚拟现实技术的5.5m电力电缆隧道内部布置方案研究(Research on internal layout scheme of5.5 meters power cable tunnel based on virtual reality technology)［J］．华东电力(East China E-lectric Power)，2010，38(4):540-541．

［2］王晓彤，林集明，陈葛松，等(Wang Xiaotong，Lin Jiming，Chen Gesong，et al．)．广东—海南500kV海底电缆输电系统电磁暂态研究(Electromagnetic transient analysis of 500kV submarine cable transmission system from Guangdong to Hainan)［J］．电网技术(Power System Technology)，2008，32(12):6-10．

［3］李景禄，郑瑞臣(Li Jinglu，Zheng Ruichen)．关于接地工程中若干问题的分析和探讨(Discussion on relative parameters in grounding technology)［J］．高电压技术(High Voltage Engineering)，2006，32(6):122-124．

［4］施虎，杨华勇，龚国芳，等(Shi Hu，Yang Huayong，Gong Guofang，et al．)．盾构掘进机关键技术及模拟实验台现状与展望(Key technologies of shield tunneling machine and present status and prospect of test rigs for tunneling simulation)［J］．浙江大学学报(Journal of Zhejiang University)，2013，47(5):741-748．

［5］费万民，张艳莉，吕征宇，等(Fei Wanming，Zhang Yanli，Lv Zhengyu，et al．)．电力系统中直流接地电阻检测和接地故障点探测的方法研究(Study on methods of measuring insulation resistance between ground and dc power supply and detecting fault grounded point)［J］．电工电能新技术(Advanced Technology of Electrical Engineering and Energy)，2001，20(3):60-63．

［6］卢中山，张小青，李建修(Lu Zhongshan，Zhang Xiaoqing，Li Jianxiu)．一种有效的接地电阻测量方法(Method to efficiently measure grounding resistances)［J］．电工电能新技术(Advanced Technology of Electrical Engineering and Energy)，2010，29(4):44-47．

［7］李增，吴广宁，付龙海，等(Li Zeng，Wu Guangning，Fu Longhai，et al．)．双层结构土壤模型地网接地电阻的简化计算(Simplified calculation of grounding resistance of substation grounding system in the two-layer soil)［J］．高电压技术(High Voltage Engineering)，2008，34(1):45-48．

［8］杨易旻，彭敏放，王嘉家，等(Yang Yimin，Peng Minfang，Wang Jiajia，et al．)．基于矩量法的接地网接地电阻计算(An algorithm for grounding resistance based on the Galerkin’s moment method)［J］．电力科学与技术学报(Journal of Electric Power Science and Technology)，2008，23(2):56-59．

［9］马信山，张济世，王平(Ma Xinshan，Zhang Jishi，Wang Ping)．电磁场基础(Fundamentals of electromagnetic fields)［M］．北京:清华大学出版社(Beijing: Tsinghua University Press)，2008．

［10］解广润(Xie Guangrun)．电力系统接地技术(Power system grounding technology)［M］．北京:中国电力出版社(Beijing:China Electric Power Press)，1999．

(，cont．on p.74)(，cont．from p.49)

Simplified formula for calculating grounding resistance of grounding system using tunnel foundation in cable tunnel

DU Xue-long1，QIU Tian-jiao2，ZHANG Xiao-ying2，MA Xue-liang2，YIN Fan2，GUO Jian2，ZOU Jun1
(1．Department of Electrical Engineering，Tsinghua University，Beijing 100084，China; 2．Beijing Electric Power ECO INST，Beijing 100055，China)

The grounding resistance is one of the important parameters for the safe operation of the grounding system in cable tunnel．Based on the simulation analysis，a simplified formula for calculating the grounding resistance of grounding system using the tunnel foundation(GSTF)is provided in this paper．Firstly，the simplified grounding system of cable tunnel is obtained and the corresponding finite element simulation model is built．Then，the influence of the number of steel bar layer，the number of steel bar，the conductivity of cement layer and the thickness of cement layer on the grounding resistance is analyzed．At last，according to the simulation results，the problem that solving the grounding resistance of the complex grounding system in tunnel can be simplified to that solving the grounding resistance of the buried cylindrical conductor whose grounding resistance can be obtained easily．The results indicate that the accuracy of the simplified formula can meet the needs of engineering calculation．And the expression is suitable for calculating the grounding resistance of GSTF in cable tunnel．

cable tunnel;grounding system;grounding resistance

TM152

A

1003-3076(2014)11-0044-06

2014-09-07

杜学龙(1988-)，男，山东籍，博士研究生，研究方向为接地系统的研究分析;仇天骄(1985-)，女，北京籍，工程师，硕士，研究方向为电力电缆设计及相关技术研究。