矿用UHF RFID阅读器分形天线的设计

杨友良 苏立虎 孟凡伟 马翠红

(河北联合大学电气工程学院，河北 唐山 063009)

0 引言

天线处于RFID阅读器系统的最前端，阅读器天线形成的电磁场范围、强度和形状决定了标签感应的灵敏度、作用距离和范围大小。阅读器天线的输入参数如阻抗、带宽，则影响RFID阅读器与天线的匹配程度，决定了阅读器的能量及数据发送和接收质量的好坏。因此，天线性能的好坏对整个射频识别系统的性能具有重要的影响［1］。

Manderblot在1975年提出了分形理论。该理论指出具有分形结构的物体一般都有比例自相似性和空间填充性的特点。国内外研究人员对Sierpinski单极子、Sierpinski贴片、Koch曲线单极子、Koch贴片等分形结构的天线做了大量研究工作，证实了分形结构的天线具有良好的尺寸缩减特性，可以在有限的空间内大幅度提高天线效率［2］。为此，本文采用分形理论和HFSS软件来构建新型的天线模型。

1 天线设计的理论分析

RFID阅读器天线大多属于传统类型的微带天线，由于结构、安装和使用环境等变化多样，并且阅读器产品朝着小型化甚至超小型化方向发展，常规的方法虽然可以通过提高基片介电常数、加载短路棒、加载缝隙，实现贴片天线的小型化设计，但是这些方法不但对天线的性能有较大影响，而且会导致阅读器天线的成本上升，加大仿真设计的难度。

本文从分形理论入手，采用一种简单的分形结构，满足了RFID阅读器天线结构紧凑、低剖面、小型化、圆极化以及识别距离远的设计要求。

1.1 分形天线理论

所谓分形天线，是指几何属性上具有分形特征的天线。世界上第一个分形天线是由美国科学家Dr.Nathan Cohen于1988年完成的，而对分形天线进行系统的研究是从1995年8月Cohen发表的第一篇有关分形天线方面的文章开始的。随后，国际上很多大学和科研机构开始对分形天线进行研究。分形天线是分形电动力学的众多应用之一。天线与阵列的分形设计是电磁理论与分形几何学的融合，如我们熟悉的螺旋天线和对数周期天线等频率无关天线都是分形天线。分形天线已经存在多年，但直到分形技术应用后，它的性能才得以充分的理解。

传统的微带天线要实现其双频和多频工作通常需要采用多个辐射单元的天线或电抗性负载贴片天线或多频介质谐振天线，这些都增加了天线的复杂性，同时，也增加了制作的难度和成本。现代无线通信要求采用低剖面、小尺寸、多频带(宽频带)、可集成的天线，分形天线能更好地满足这些要求。分形是通过迭代产生的分数维自相似结构，其整体与局部、局部与局部之间都具有自相似性。因此，分形是一种与标度无关的几何，与宽带天线的频率无关性比较相似。将分形应用于天线的设计主要是用来实现天线小型化和天线的多频特性，分形天线解决了传统天线的两个局限性。

①通常天线的性能都依赖于天线的电尺寸。这就意味着对于固定的天线尺寸，主要天线参数将随着工作频率的改变而改变。分形的自相似性使分形天线具有多频和宽频特性。

② 分形的空间填充性，使一些尺寸得到减缩［3］。

1.2 两种经典的分形结构

1.2.1 Minkowski分形环的迭代生成

假设复平面上给定两点，坐标分别为a0和b0。上标0表示初始单元，1表示生成单元，下标表示点排号。对于初始单元，有a0=a0(0)、a1=a1(0);对于生成单元，设a0(1)=a0(0)、a5(1)=a1(0)，令:

图1 Minkowski分形环的迭代生成过程Fig.1 Iterative generation process of Minkowski fractal ring

1.2.2 Sierpinski毯结构

国内外关于Sierpinski毯结构天线研究的很深入，其构造过程为:将一个正方形等分分割成9个小正方形，去掉中间的小正方形，剩下8个小正方形;对剩下的小正方形分别再做9等分分割，并去掉各自中间的小正方形，剩下64个小正方形;如此反复分割操作，直至无穷，就构造成 Sierpinski方毯［5］，其示意如图 2所示。

图2 方形Sierpinski毯结构Fig.2 Structure of square Sierpinski blanket

1.3 圆极化理论

圆极化的关键是激励两个极化方式的线极化波，当这两个极化方式的线极化波幅度相等、相位相差90°时，就能得到圆极化波的辐射。获得圆极化特性的馈电方式有两种，一种是单点馈电，另一种是正交馈电。本节主要介绍单点馈电圆极化微带天线的实现原理。

当同轴线的馈电点位于辐射贴片的对角线位置时，可以激发TM01和TM10两个模式，这两个模式的电场方向互相垂直。在设计中，辐射贴片的长度L和宽度W相等，这样激发的TM01和TM10两个模式的频率相同、强度相等，而且两个模式的电场的相位差为零。若辐射贴片的谐振长度为LC，微调谐振长度略偏离谐振，即一边长度为LC+a，另一边长度为LC－a。前者对应一个容抗Y1=G－jB，后者对应一个感抗Y1=G+jB，只要调整a的值，使得每一组的电抗分量等于阻抗的实数部分，即B=G，则两阻抗的大小相等，相位分别为+45°和－45°，这就满足圆极化条件，从而构成圆极化天线［6］。

Kalio和Carver Coffey研究证明，当理论上L/W=1.029，即 a=0.0143LC时，TM01和 TM10两个模式的相位差为90°。另外，由实际经验可以得到，圆极化结构的50 Ω馈电点位于辐射贴片对角线上，且馈电点和辐射贴片顶点的距离在(0.35～0.39)d(d为介质基板的厚度)之间。假设馈电点到辐射贴片的中心距离为L1，则 L1位于(0.11 ～0.15)LC之间。

1.4 最大读取距离的计算

当无源RFID系统正常工作时，阅读器能够激活标签，标签获取能量返回信号被阅读器识别的最大距离Rmax。阅读器天线在方向(θtrans，φtransRmax)上传播距离R的功率谱密度为:

式中:θtrans为发射天线的水平方向角度;φtrans为发射天线的垂直方向角度;Ptrans为阅读器发射天线的发射功率;Gtrans为阅读器发射天线的增益;EIRP为阅读器等效面的辐射功率，它等于发射功率与增益的乘积［7］。

根据Friis空间公式，得到RFID标签天线的接收功率表达式为:

式中:Gtag(θtag，φtag)为标签接收天线在(θtag，φtag)方向的增益;λ为波长;为天线极化损耗因子，通常对于线极化和圆极化天线，极化损耗因子都是0.5。

由式(4)～式(6)可得到:

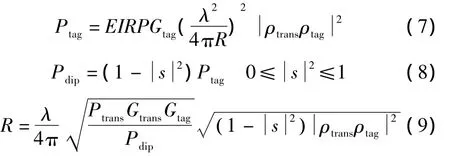
式中:Pdip为芯片接收功率;为功率发射系数;1－为标签的接收天线与标签芯片之间的功率传输系数;R为阅读器与标签之间的距离。

当谐振频率为922 MHz时，阅读器与标签间的识别距离最大。根据中国超高频频段标准和所选择射频芯片(AS3992)的相关参数，EIRP=2 W、Gtag=3 dB、f=922 MHz、Pdip= －18 dBm、c=3.0 ×108m/s，代入公式得到 Rmax=7.16 m，此时阅读器的灵敏度为 －57 dBm。本文用到的阅读器灵敏度为－80 dBm，该阅读器可以接收到标签方向散射回来的信号，满足设计要求。

2 天线的优化和仿真

根据中国UHF频段射频识别技术的标准，所设计的天线应满足以下指标。

①工作频率能够完全覆盖920～925 MHz;

②当中心频率为922 MHz时，增益达到－30 dB;

③增益在－10 dB以下的带宽大于10 MHz;

④驻波比＜2，达到了较高的圆极化性能;

⑤和传统天线相比，尺寸缩减;

⑥识别距离大于5 m。

2.1 分形天线的建模

方形Sierpinski毯天线具有明显的多频特性，但是尺寸上还是显得过大;Minkowski微带贴片天线尺寸较小，但是频带较窄。匈牙利人Vicsek提出了一个操作方法，将一个正方形9等分，只保留中心和四个角上的小正方形，其余的去掉，得到这样的图形称为1阶Vicsek图形。

如果将中间的贴片变大，保持外围尺寸不变，那么便得到图 3 所示的结构［8－12］。

图3 变形后的1阶Vicsek图形Fig.3 The 1storder Vicsek graphics after deformation

若采用1阶Vicsek的模型，通过HFSS软件仿真后，天线的带宽较窄且增益较小。因此，本文对四个角上及中间的正方形进行开槽，对模型加以改进，以增大天线的频带宽度，提高增益。

改进后的天线模型正面如图4所示。

图4 改进后的天线模型正面图Fig.4 Front views of the improved antenna model

2.2 天线的优化和仿真

通过使用HFSS商业软件对改进后的天线进行仿真，得到天线的扫频分析仿真图如图5所示。

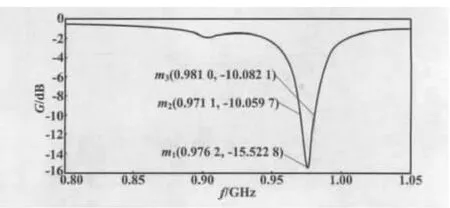
图5 改进后的天线扫频分析仿真图Fig.5 Frequency sweep analysis simulation of the improved antenna

从图5可以看出，天线的中心频率为0.9762 GHz，不满足中国超高频频段的标准。对天线模型再次改进，采用的方式为对地板开槽，以使谐振频率左移。再次改进后的地板模型如图6所示。

经多次优化仿真，最后确定所开槽的宽度为2 mm，长度为24.5 mm。此时使用HFSS软件对天线进行仿真，得到再次改进后的天线扫频分析仿真图如图7所示。

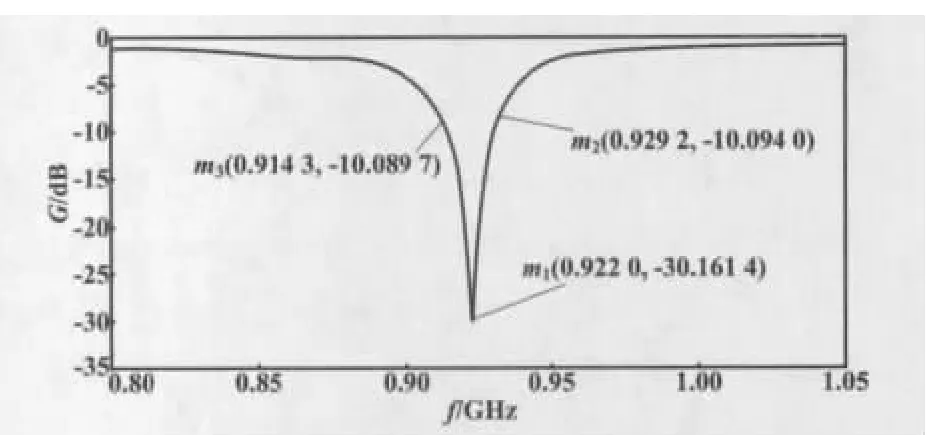
图7 再次改进后的天线的扫频分析仿真图Fig.7 Frequency sweep analysis simulation of the antenna improved once again

从图7可以得出，谐振频率为922 MHz，增益为－30.1614 dB，－10 dB 以下频带宽度为15 MHz，满足设计要求。

天线的输入阻抗仿真图如图8所示。

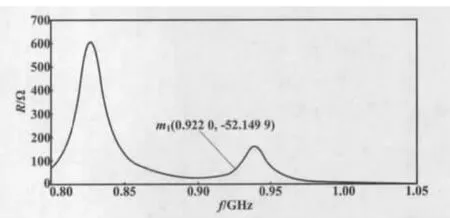
图8 天线输入阻抗仿真图Fig.8 Antenna input impedance simulation

从图8可以看出，当谐振频率为922 MHz时，天线的输入阻抗为52 Ω，接近50 Ω，满足设计要求。

为了实现天线的圆极化，天线的电压驻波比＜2，使用HFSS软件进行仿真，得到电压驻波比仿真图如图9所示。

从图9可以得出，当频率位于914.3～929.2 MHz范围内，天线的电压驻波比＜2，能够很好地实现天线的圆极化，满足设计的要求。

图9 电压驻波比VSWR仿真分析图Fig.9 Voltage standing wave ratio simulation analysis

3 结束语

设计的天线经过仿真，中心频率为922 MHz，增益达到－30 dB;当增益在－10 dB以下，频率从914 MHz上升至929 MHz时，带宽达到15 MHz，完全覆盖中国的超高频频率(920～925 MHz)的范围;电压驻波比＜2，具有很好的圆极化性能;归一化输入阻抗为52 Ω。各项参数都很好地满足设计要求，完全符合中国超高频频段的标准。天线长度和宽度尺寸为60 mm×60 mm，比传统的90 mm×90 mm缩减了33%，比改进型传统尺寸70 mm×70 mm缩减了14.29%。设计的阅读器天线理论识别距离最大达到7.16 m，适用于煤矿井下人员定位系统。

［1］王保云.物联网技术研究综述［J］.电子测量与仪器学报，2009(12):1－7.

［2］朱华，姬翠翠.分形理论及其应用［M］.北京:科学出版社，2011.

［3］孙博文.分形算法与程序设计［M］.北京:科学出版社，2004.

［4］杨汉华.矿用RFID分形天线的设计与研究［D］.镇江:江苏大学，2008.

［5］谢晶晶，赵东东.UHF Passive RFID标签最大距离的研究［J］.电子测量技术，2012，35(3):45 －49.

［6］佘开，何怡刚，李兵，等.无源超高频RFID系统链路预算分析［J］.仪器仪表学报，2010，31(5):974 －978.

［7］唐志军，席在芳，詹杰.无源反向散射RFID系统识别距离的影响因素分析［J］.计算机工程应用，2012，48(23):85 －89.

［8］Yoon I，Kim D.Adaptive defogging with color correction in the HSV color space for consumer surveillance system［J］.IEEE Transactions on Consumer Electronics，2012，58(1):111 －116.

［9］Leichter I.Mean shift trackers with cross-bin metrics［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，2012，34(4):695－706.

［10］李明洋，刘敏，杨放.HFSS天线设计［M］.北京:电子工业出版社，2011.

［11］李圣明，施游互，孝番林，等.一种低成本MVSAT天线指向控制系统设计［J］.自动化仪表，2008，29(4):33 －35.

［12］邹丽娟，黄建国.基于圆锥扫描的舰载卫星电视天线跟踪系统［J］.现代雷达，2004，26(10):68 －70.