Welch功率谱估计算法在相位噪声测量中的应用
2014-06-01任全会于彦峰
任全会 于彦峰
(郑州铁路职业技术学院电子工程系,河南 郑州 450052)
0 引言
描述信号短期频率稳定度非常重要的指标是相位噪声,在信号处理和通信领域,衡量系统性能的关键指标也是相位噪声,所以相位噪声测量技术在电子测量领域的地位越来越重要。相位噪声测量一个很重要的方法是鉴相法,其关键技术是对鉴相结果进行功率谱估计。传统的功率谱估计方法虽然频谱分辨率很高,但是频谱分布很不稳定,无法反映信号的时变特性[1]。Welch功率谱估计算法利用分段平均和时间窗函数的思想能很好地解决这些问题。该方法根据不同的噪声信号对Welch法的参数进行调整,能很好地改善相位噪声功率谱估计性能。
1 相位噪声测量原理
相位噪声可表示为:
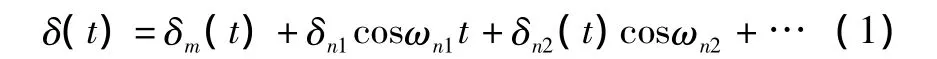
式中:δm(t)为随机相位噪声;δni(t)cosωnit为周期性杂散信号。
因为噪声在实际应用中很小,所以设δm(t)<<1,被测信号可表示为:
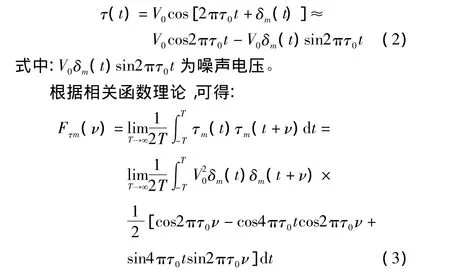
因为 δm(t)δm(t+υ)和cos4πτ0t不相关,当 υ 为定值时,cos2πτ0υ 是常数,所以:
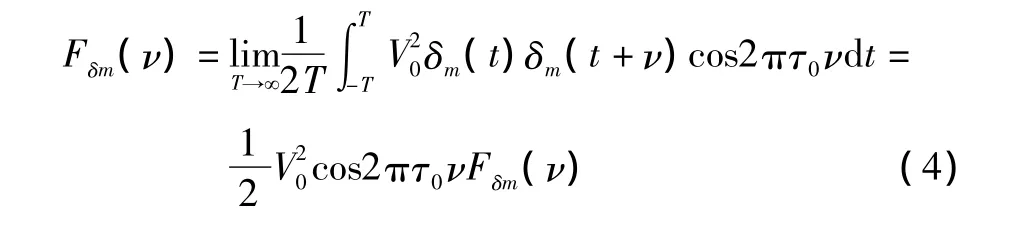
根据维纳-辛钦定理,相位噪声δm(t)的双边带功率谱密度Qδm(ω)2可以表示为:

噪声电压Vm(t)的双边带功率谱密度Qτm(ω)2可表示为:

由式(11)可以看出,被测信号的单边带相位噪声可以用噪声电压的功率谱密度表示[2]。
2 噪声功率谱估计方法
2.1 Welch法性能分析
Welch法采用分段平均的方法,同时允许数据之间有重叠,这样谱估计过程中被平均的周期图数就更多,功率谱估计的方差性能可得到很好的改进。对50%重叠和无重叠两种情况进行了仿真,得到的谱估计性能曲线如图1所示。
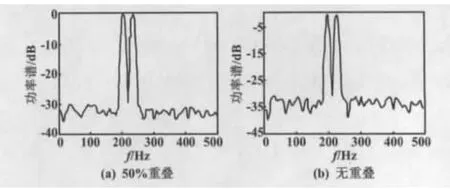
图1 重叠长度对谱估计性能影响曲线Fig.1 Influence curves of overlap length on the performance of spectral estimation
由图1可以看出,分段重叠对功率谱估计的改变不明显。
在计算周期图时可以使用时间窗,因为时间窗对序列末端数据的加权较小,这样就能很好地控制估计结果的偏差。同时窗函数可以平衡分辨率和频谱泄漏[3]。
Welch法功率谱估计式可表示为:

Welch法谱估计结果受时间窗函数的影响非常大。几种窗函数仿真图如图2所示。从图2可以看出,因为Rectangular窗的旁瓣衰减较小,所以分辨率相对Hamming窗和Kaiser窗要好;因为Hamming窗和Kaiser窗的旁瓣衰减较大,所以分辨率较低;Rectangular窗的谱分析噪声水平最高[4]。
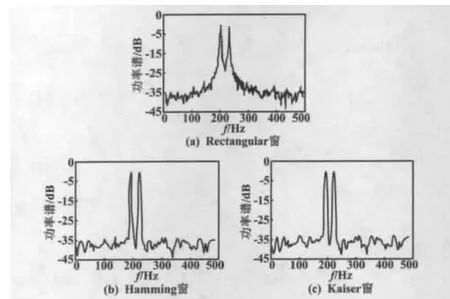
图2 Welch法不同窗函数对比图Fig.2 Comparison of different window functions of Welch method
2.2 谱估计方法改进
相位噪声测量充分利用Welch法中数据分段的思想,结合噪声信号是鉴相器输出等周期分段的特点,对噪声信号进行功率谱估计,这样就能完成对相位噪声的测量。具体的分段示意图如图3所示。
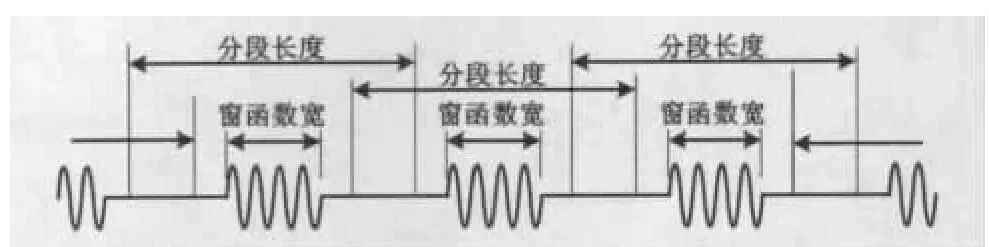
图3 Welch法数据分段和加窗方法示意图Fig.3 Schematic diagram of Welch method data segmentation and windowing method
Welch法估计信号噪声功率谱的主要优点是数据分段思想,在实际的应用当中,Welch法加窗的减小能减小鉴相器在脉冲开关瞬间的数据计算权值。但由于分段具有平均的作用,会影响估计结果的分辨率[5-7]。这个问题可以通过增加采样样本点数来解决。
相位噪声测量中,Welch法和传统方法比较如表1所示。

表1 Welch法和传统方法比较Tab.1 Comparison of Welch method and traditional method
3 测试结果
将一个由高斯白噪声和闪烁噪声组成仿真噪声的正弦信号作为被测信号,其表达式为:

式中:δ(t)为仿真噪声;f=1000 Hz。
通过Matlab软件进行仿真,其结果如图4所示。
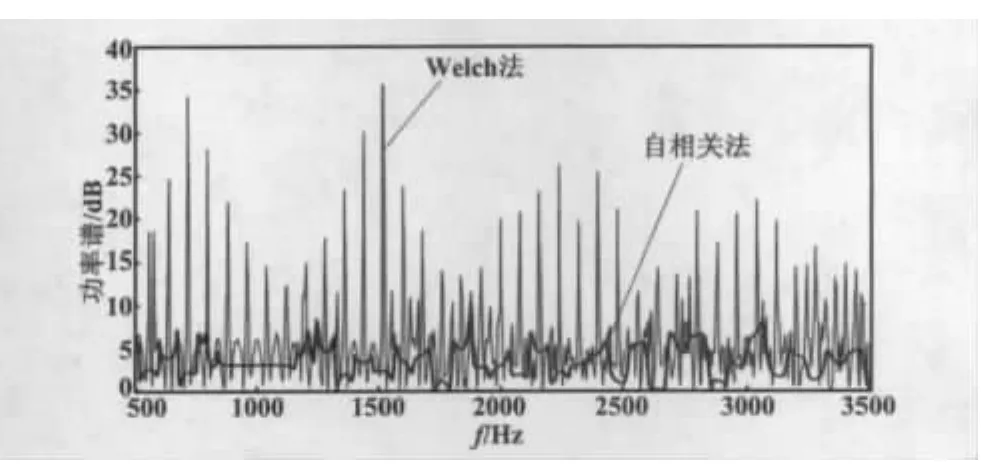
图4 Welch方法和自相关法仿真结果比较图Fig.4 Comparison of the simulation results of Welch method auto-correlation method
相关数据表明,利用自相关法噪声功率谱估计结果的均方误差为23.88,利用Welch法噪声功率谱估计结果的均方误差为9.264。显然,利用Welch法进行噪声功率谱估计更具正确性。
4 结束语
相位噪声测量利用基于Welch功率谱估计算法,充分利用数据分段和时间窗函数的思想,即使在噪声功率相互混叠造成噪声功率减退时也能完成相位噪声的测量。
与传统的自相关法相比,Welch法具有能适应噪声信号的随机性和脉冲性的优点。此外,谱估计的方差性能可以通过重叠度的数据分段来提高,谱估计的偏差和分辨率特性可以通过时间窗函数进行调整,鉴相器瞬态输出的影响可以通过时间窗函数的权值消除。Welch法方法可以很好地测量噪声,同时噪声功率谱均方差也大大降低。
[1]贺静波,胡生亮,罗亚松,等.基于随机微分的相位噪声统计特性[J].中国激光,2012,39(10):1 -5.
[2]杜保强,周渭.基于等效鉴相频率的新型相位噪声测量系统[J].吉林大学学报:工学版,2010,40(5):1426 -1432.
[3]赵慧,冬黑勇,乔树山.OFDM电力线通信系统的相位噪声估计与补偿[J].电视技术,2012,36(17):122 -125.
[4]张峰,石现峰,张学智.Welch功率谱估计算法仿真及分析[J].西安工业大学学报:工学版,2009,29(4):353-356.
[5]沈志远,王黎明,陈方林.基于有限长序列分析的Welch法谱估计研究[J].计算机仿真,2010,27(12):391 -395.
[6]赵小龙,王玉平,鲍丽红.相关杂波的产生及功率谱估计技术研究[J].自动化与仪器仪表,2013(3):18-20.
[7]王娜,郑德忠,孙海艳,等.基于感知滤波器与统计方法的语音增强新算法[J].自动化仪表,2010,31(12):8 -10.
