NMOHEMS布放系统可靠性的Petri网分析方法

翁兴国 王晓蕾 叶 松 于利军 陈振涛

(陆军航空兵学院飞行理论系1，北京 通州 101123;解放军理工大学气象海洋学院2，江苏 南京 211101)

0 引言

新型远海机动水文环境现场监测系统［1－2］(new mobile offshore hydrologic environment monitoring system，NMOHEMS)是一种基于无人机技术、流星余迹通信技术［3］和海洋现场探测技术［4］的深远海机动海洋水文环境监测系统。该系统主要由无人机及其控制发射机动单元、舰船和岸基用户单元、流余主站和现场探测单元四大部分组成。NMOHEMS采用无人机机载方式，实现现场探测单元的超远距离目标区域的现场投放任务。

NMOHEMS自动化程度比较高，系统的结构复杂，因此对其可靠性要求也较苛刻。可靠性工作应贯穿于NMOHEMS的概念设计、方案设计、技术设计、生产、试验、操作使用直至退役的全寿命过程，其主要的内容包括可靠性预测、可靠性设计、可靠性试验、可靠性分析和评估等［5］。由于篇幅有限，本文只对NMOHEMS布放系统进行可靠性分析。

结合故障树直观性的优点，综合利用数学化和图形化的分析工具Petri网模型对NMOHEMS布放系统进行可靠性分析［5］。由于故障树模型难以描述系统的动态特性，不易表现故障发生的时序关系，因此在建立故障树的基础上，使用Petri网模型对故障树进行描述和简化，解决故障树难以描述系统动态特性的瓶颈，从而提高系统可靠性设计和分析的效率。

1 NMOHEMS布放系统

NMOHEMS布放系统主要由机载单元、降落伞单元和现场探测单元三个模块组成，系统结构示意图如图1所示。当无人机到达指定的海域后，通过驱动电路激活投掷执行机构按顺序依次布放现场探测单元。每一枚现场探测单元释放出仓后，安装在尾部的降落伞自动打开。由于受无人机空间荷载的限制，将现场探测单元设计成伸缩式结构。该单元主要由主浮体和剖面探头承载单元两部分组成［6］。投掷之前，剖面探头承载单元收缩在主浮体里面;投掷之后，其在下降过程中要求实现自动有效膨胀，膨胀的动力来源于化学反应产生的气体。现场探测单元以气压弹射的方式进行布放，以免降落伞在现场探测单元释放后对无人机的飞行造成安全隐患。投掷仓投放的切换、自动加压系统的加压、投放前后投掷仓仓门的打开和关闭由机载单元完成。降落伞单元主要完成降落伞的自动打开以及现场探测单元入水后的自动脱离。现场探测单元是布放系统的核心，主要完成现场探测单元的自动膨胀、温度、深度以及盐度等剖面信息的获取。

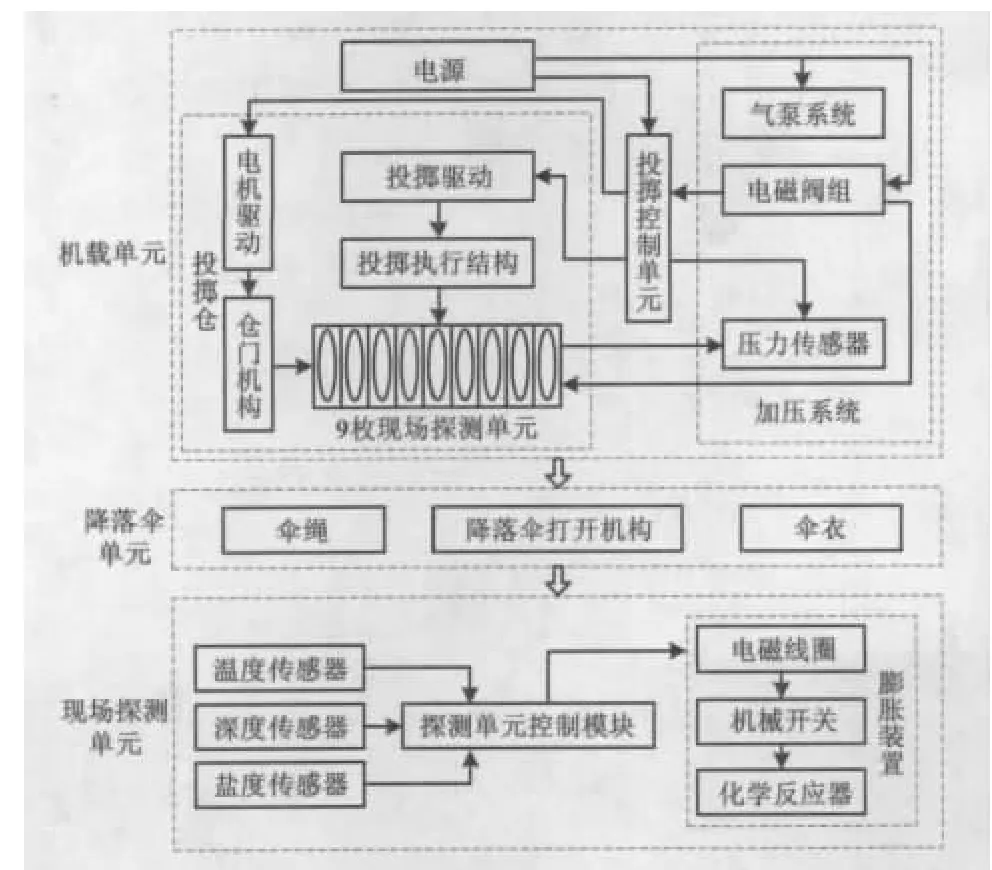
图1 系统结构示意图Fig.1 Schematic diagram of system

2 NMOHEMS布放系统故障树分析

故障树分析模型是一种经典的可靠性分析方法，它使用规定的事件符号和逻辑门符号表示系统故障传播的逻辑关系，从而演绎NMOHEMS布放系统各事件之间的因果关系。布放系统以无人机布放失效为顶事件，先逐层对布放系统各模块进行图形演绎，找出导致布放任务失败的全部直接原因和间接原因;接着寻找布放失败发生的原因和原因组合，识别布放失败的所有故障模式;最后分析判断潜在的故障，便于方案的修改和设计。

在不考虑NMOHEMS布放系统与其他系统关联的情况下，将布放系统的事件进行编码，理清事件发生的时序关系，得到系统的故障树如图2所示。从图2可以看出，根据NMOHEMS布放系统各事件之间的逻辑关系，能够初步观察到故障的传递路径。

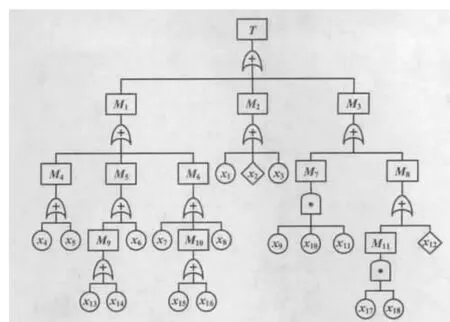
图2 NMOHEMS布放系统的故障树模型Fig.2 The fault tree model of deployment system of NMOHEMS

系统故障树的各事件的编码表如表1所示。

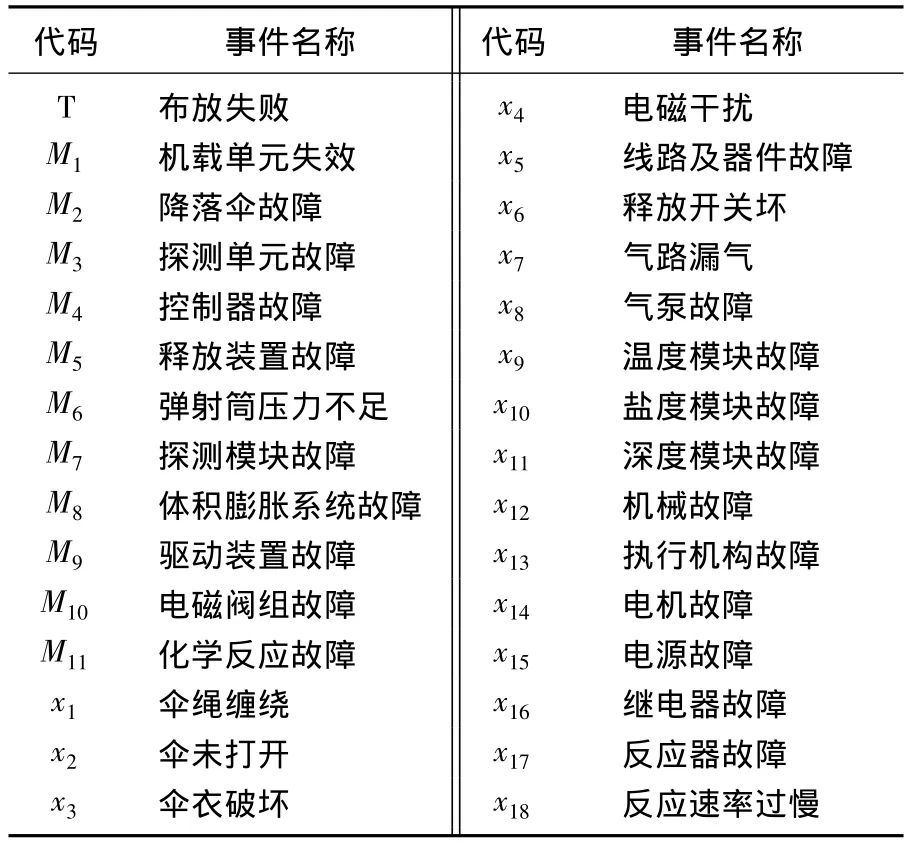
表1 事件名称及代码符号Tab.1 Event names and code symbols

3 布放系统的Petri网模型

故障树模型虽然能够图文兼备，清楚表达各个事件之间的逻辑关系，但在演绎故障动态传播方面稍显不足。此外，对于复杂系统，故障树定量分析繁杂而冗长，实际计算比较困难。Petri网模型可以弥补故障树的不足，Petri网能够直观地描述系统的动态过程，使用Petri网的关联矩阵也可以方便求出系统的最小割集，为定量分析奠定基础。Petri网还可以很好地应用数学化的方法诊断系统故障的动态传递过程。Petri网模型将故障树的各种逻辑连接关系简化为只由库所和变迁组成、以有向弧为连接边的网络，使系统的故障模型简洁、易懂，故障的传播关系一目了然。NMOHEMS布放系统故障树的Petri网模型如图3所示。图3中，Pi为故障树中顶事件、中间事件和基本事件的库，ti为故障树中事件之间逻辑关系的变迁。

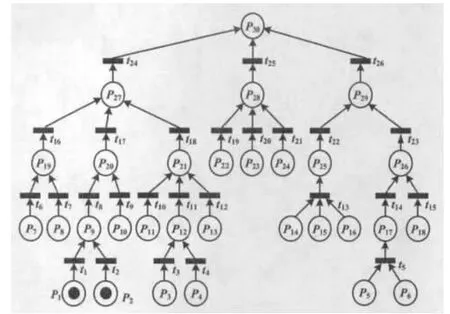
图3 NMOHEMS布放系统Petri网模型Fig.3 Petri network model of deployment system of NMOHEMS

3.1 关联矩阵法求最小割集

Petri网求最小割集的方法主要有路径搜索法、库所矩阵法和关联矩阵法。但是，路径搜索法会对大型的Petri网模型造成组合爆炸困难问题［7］，而库所矩阵法难以进行故障的诊断分析，因此本文采用关联矩阵法求解系统的最小割集。Petri网的结构可以用一个矩阵来表示。若从库所P到变迁t的输入函数取值为非负整数ω，即为I=(P，T)=ω，则用从P到t的一段有向弧并旁注ω表示;若从变迁t到库所P的输出函数取值为非负整数ω，即为O=(P，T)=ω，则用从t到P的一有向弧并旁注ω表示。特别地，若ω=1，则不必标注;若I=(P，T)=0或O=(P，T)=0，则不必画弧。I和O均可表示为n×m非负整数矩阵，O与I之差A=O－I称为关联矩阵［8］。本文研究规范网，所以ω=1。NMOHEMS布放系统的关联矩阵为:

根据式(1)，求解NMOHEMS布放系统Petri网最小割集的步骤如下［9］。

①观察关联矩阵，找到没有－1所在的行，即第30行(布放失败所在行)，记录下每个1所在的列分别为第24、25、26 列。

②从第24列出发，搜索此列并记录下这一列中－1所在的行为27。

③继续搜索第27行，记录下这一行中1所在的列为16、17、18，则说明同为 P27的输入库所，它们之间为“相或”关系。按步骤②循环查找，第16列中－1所在行为19，这一行中1所在的列为6、7，继续寻找第6列－1所在行，－1所在行为7，即有:P19=P7+P8。同样的方法查找第17、18列，可得:

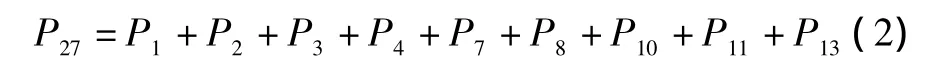
④再从第25列出发，重复步骤②、③，即搜索第28行，可得:

⑤从第26列出发，重复步骤②、③，即搜索第29行，可得:

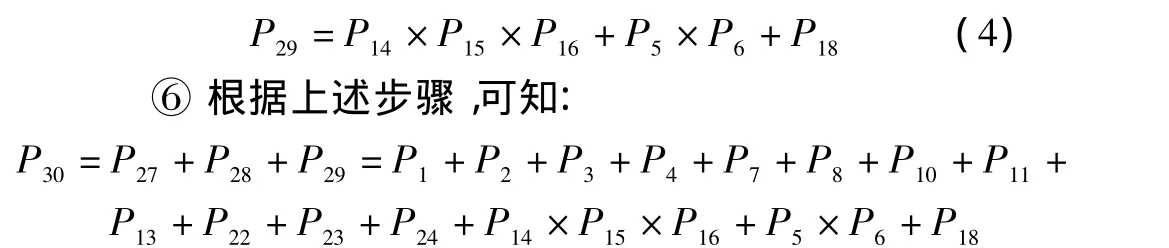
⑦使用布尔吸收率或素数法，求得最小割集。

3.2 系统故障的诊断

故障的产生和传播是一个典型的动态过程，利用Petri网可以很好地描述故障现象的动态传播过程以及事件发生的时序关系［10］。关联矩阵是求解系统状态变迁的主要工具，系统状态变迁的关系式为:

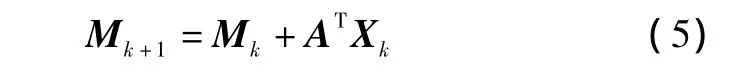
式中:Mk为点火前的系统故障的初始标志集;Mk+1为点火后的系统故障的结果标志集;A为关联矩阵;Xk为第k次点火转移序列。

由式(5)的递推关系，可得:

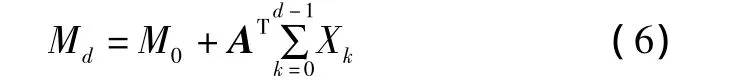
式中:M0为点火前的系统故障的初始标志集;Md为点火后的系统故障的结果标志集;A为关联矩阵;Xk为被激发变迁点火一次的发生数向量值。

假设系统的初始状态是执行机构和电机同时出现故障，则故障的初始状态为 M0=［1，1，0，…，0］。按照式(5)、式(6)的算法计算得到后续状态(M1～M4)的表达式为:

4 定量分析

NMOHEMS布放系统的动态性质和结构性质是NMOHEMS可靠性分析和可靠性设计的重要内容。系统顶事件发生的概率以及底事件的重要度是定量分析的核心，也是可靠性分析考虑的主要性能参数，便于用户根据具体的可靠性结果调整优化概念设计方案。在底事件发生概率已知的条件下，通过最小割集求出顶事件发生的概率，并进一步明确各个模块的重要度。NMOHEMS布放系统中各个模块的重要性各不相同，例如有的模块一旦出现故障就会引起系统故障，有的则不然。因此，对底事件引发顶事件发生的重要度进行分析，使用冗余设计的思想备份系统的重要核心部件，可以使系统的可靠性得到大大提高。

设顶事件发生的概率为P(T)，由关联矩阵法得到的布放系统的最小割集为C1={P1}、C2={P2}、C3={P3}、C4={P4}、C5={P7}、C6={P8}、C7={P10}、C8={P11}、C9={P13}、C10={P22}、C11={P23}、C12={P24}、C13={P14×P15×P16}、C14={P5×P6}、C15={P18}，则:

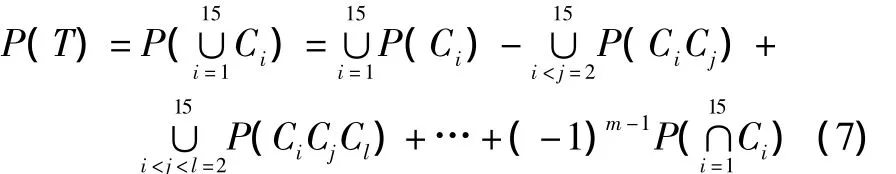
底事件的概率重要度Ip(i)和底事件的相对概率重要度IC(i)是重要度分析的主要内容。第i个底事件的概率重要度表示当第i个底事件的发生概率的微小变化而导致顶事件发生概率的变化率。设Q(q1，q2，…，q18)为顶事件发生的概率，q1，q2，…，q18分别为图 3 中的底事件 P1，P2，P3，P4，P5，P6，P7，P8，P10，P11，P13，P14，P15，P16，P18，P22，P23，P24的发生概率，则:

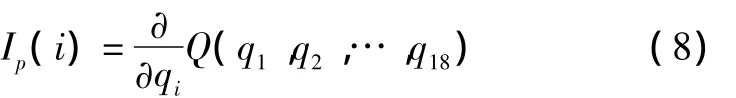
第i个底事件的相对概率重要度表示当第i个底事件的发生概率微小的相对变化而导致顶事件发生概率的相对变化率，则定义为:

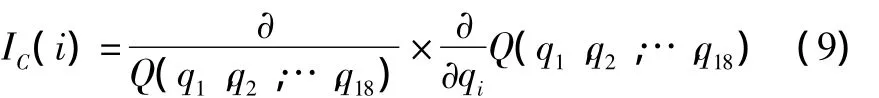
反复利用上述方法对NMOHEMS布放系统进行可靠性分析，并依据定量分析数据对系统进行冗余设计或是结构调整，可以大大提高系统的设计效率和可靠性。目前，NMOHEMS布放系统处于概念设计阶段，部分可靠性数据比较匮乏，本文只提出了NMOHEMS布放系统可靠性分析的方法。随着系统设计的进展，后续会结合具体的试验数据对系统进行反复的优化设计。

5 结束语

故障树分析法可以较好地解决MOHEMS布放系统的可靠性分析问题，但是实际应用中分析复杂、计算量大，不利于使用软件编程的方法快速有效地对系统进行评估。故障树与Petri网模型相结合的方法，一方面可以发挥故障树表达故障模式直观性的优点;另一方面可将故障树转化为Petri网模型进行分析，改进和简化故障树，弥补故障树计算量大的缺点，易于计算机程序的实现。特别是Petri网模型能方便地通过数学化的方法反映系统的状态变化和事件发展。

［1］叶松，王晓蕾，焦冰，等.NMOHEMS的概念与设计［J］.海洋技术，2010，29(1):28 －31.

［2］叶松，王晓蕾，周延年，等.远海机动水文环境监测系统技术研究与设计［J］.仪器仪表学报，2008，29(8):256 －260.

［3］周延年，叶松，郑君杰，等.利用流星余迹通信系统传输海洋数据［J］.仪器仪表学报，2008，29(8):486 －489.

［4］焦冰，叶松，王晓蕾，等.军事海洋环境海水温度信息的获取研究［C］∥第七届军事海洋战略与发展论坛论文集，北京:海潮出版社，2010:755－758.

［5］张涛，武小悦，谭跃进.Petri网在系统可靠性分析中的应用［J］.电子产品可靠性与环境试验，2003(1):60－65.

［6］刘凤，叶松，王晓蕾，等.NMOHEMS探测单元的三维建模与快速成型［J］.机械设计与制造，2012(3):68－70.

［7］谢里阳，王正，周金宇，等.机械可靠性理论与方法［M］.北京:科学出版社，2009.

［8］江志斌.Petri网及其在制造系统建模与控制中的应用［M］.北京:机械工业出版社，2004.

［9］武滢，谢里阳，李进冬.应用Petri网的关联矩阵求最小割集的新方法［J］.中国机械工程，2008，19(9):1044 －1047.

［10］Volovoi V.Modeling of system reliability Petri nets with aging tokens［J］.Reliability Engineering and System Safety，2004(84):149 －161.