基于符号相对熵的Logistic混沌系统时间不可逆性分析

2014-05-30徐红梅郭树旭

电子与信息学报 2014年5期

关键词：符号化编码符号

徐红梅郭树旭

徐红梅①②郭树旭*①

①(吉林大学电子科学与工程学院长春 130012)②(延边大学工学院延吉 133002)

混沌系统；Logistic系统；符号时间序列；相对熵；时间不可逆

1 引言

混沌现象是不含外加随机因素的完全确定性系统所表现出来的内部随机行为，具有不可预测性和不确定性。在一定的控制方法和参数范围内，系统会出现周期运动和混沌现象。现有的混沌研究方法主要有分岔图[8]，Lyapunov指数[9]，Jacobian矩阵法[10]等。这些方法直观形象，但是需要进行大量计算，对于高维迭代映射，不动点和Jacobian矩阵计算更加困难。因此，采用解析方法分析混沌现象存在一定的局限。数学理论已经证明，在1维非线性系统中得到的倍周期分岔序列与临界点附近的标度性质对于高维系统普遍适用[11]。因此，研究1维非线性系统的混沌具有普遍而重要意义，其中具有代表性的就是Logistic混沌系统。

从时间序列角度研究混沌，始于文献[12]提出的相空间重构理论。在信息论范畴，熵是对不确定性的最佳量化参数，对混沌系统产生的时间序列进行离散化处理，然后进行统计分析和量化，从而使从时间序列研究混沌成为可能。文献[13]研究了噪声相互关联时间对Logistic系统亚稳态稳定性的影响，文献[14]分析了Logistic混沌系统不同初值和系统参数的谱熵复杂性，文献[15]研究了Logistic混沌系统突变时间序列临界预警，文献[16]指出时间序列不对称性或不可逆性是混沌行为的重要标志，文献[17]研究了脑电信号的时间不可逆性，文献[18]研究了时间不可逆性与熵产之间的关系。

2 时间序列符号化和相对熵理论

2.1时间序列符号化

时间序列分析是由符号动力学、混沌时间序列分析和信息论衍生的形式较为简单的严格数学方法，是实际动力系统的高度概括和抽象。根据时间序列与符号序列拓扑共轭的特性，将若干个可能值上的离散时间序列转化为符号序列，符号化后序列能够保持原有系统动力学特性，从而将混沌系统变成一个遍历的信息源，可以采用信息论来分析符号序列。以1维单峰映射Logistic函数为例说明时间序列符号化方法。

经典Logistic函数定义为

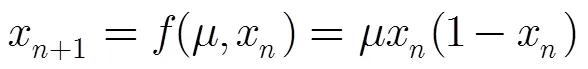
根据式(1)，经推导可得

詹寻顶着黑眼圈，坐在一堆线装书中间，几只毛笔凌乱地散落在他的身边。铺在桌上的宣纸上，密密麻麻地写满了繁体字……

2.2 相对熵理论

根据KL(Kullback-Leibler divergence)散度理论[21]，离散型随机变量的相对熵定义为

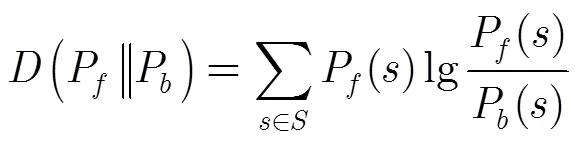
因为

相对熵反映符号序列前向分布和逆向分布的差异性。熵的本质是变化的方向性和时间的方向性，只要相对熵可以计算且大于等于零，就表明存在时间不可逆性[21]。自然界的一切自发进行过程都是朝熵增方向进行的，在熵增原理的前提下，熵值较小对应于比较有序的状态，熵值较大对应于比较无序的状态，可逆过程的熵值为零。

3 Logistic混沌系统相对熵

图1 Logistic返回映射(μ=4)

图2 Logistic混沌系统分岔图

3.1相对熵与数据长度关系

(2)当数据长度大于4000时，实际数据长度与理论要求一致，相对熵变化区间和标准差趋于稳定。

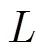
3.2 相对熵与编码长度关系

编码长度越长实验效果越明显，考虑到算法复杂度及在实际应用中的实用性，编码长度应取得短一些，综合考虑以上诸因素，编码长度取8位就能得到理想的实验结果。

3.3 数据长度=5000, 编码长度m=8时相对熵特性

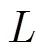
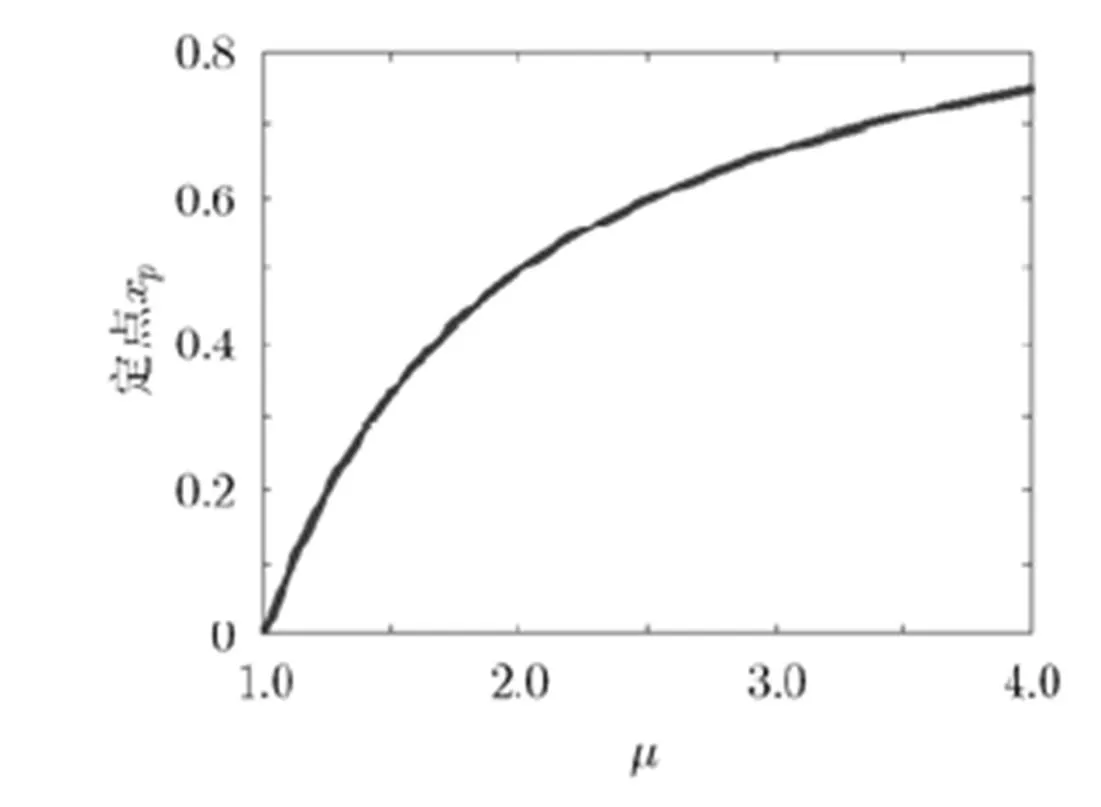
图3 Logistic混沌系统固定点随参数μ变化曲线

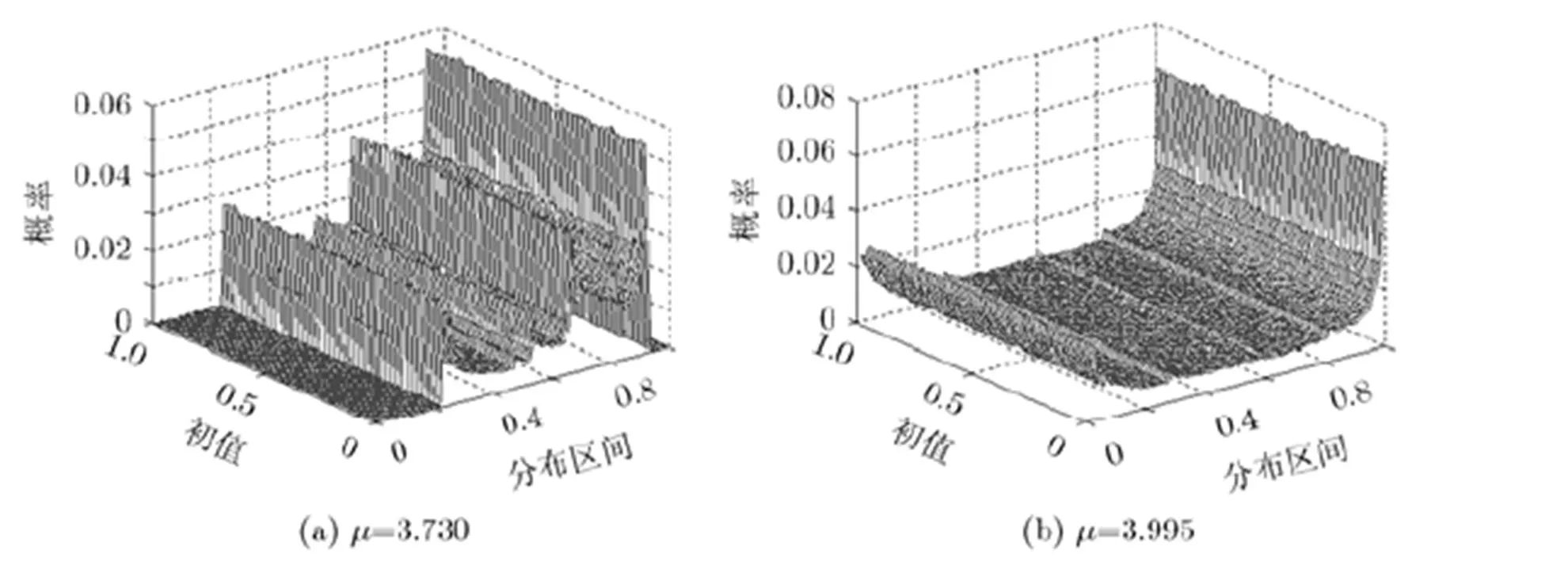
图4 Logistic混沌系统统计分布图L=100000，M=100

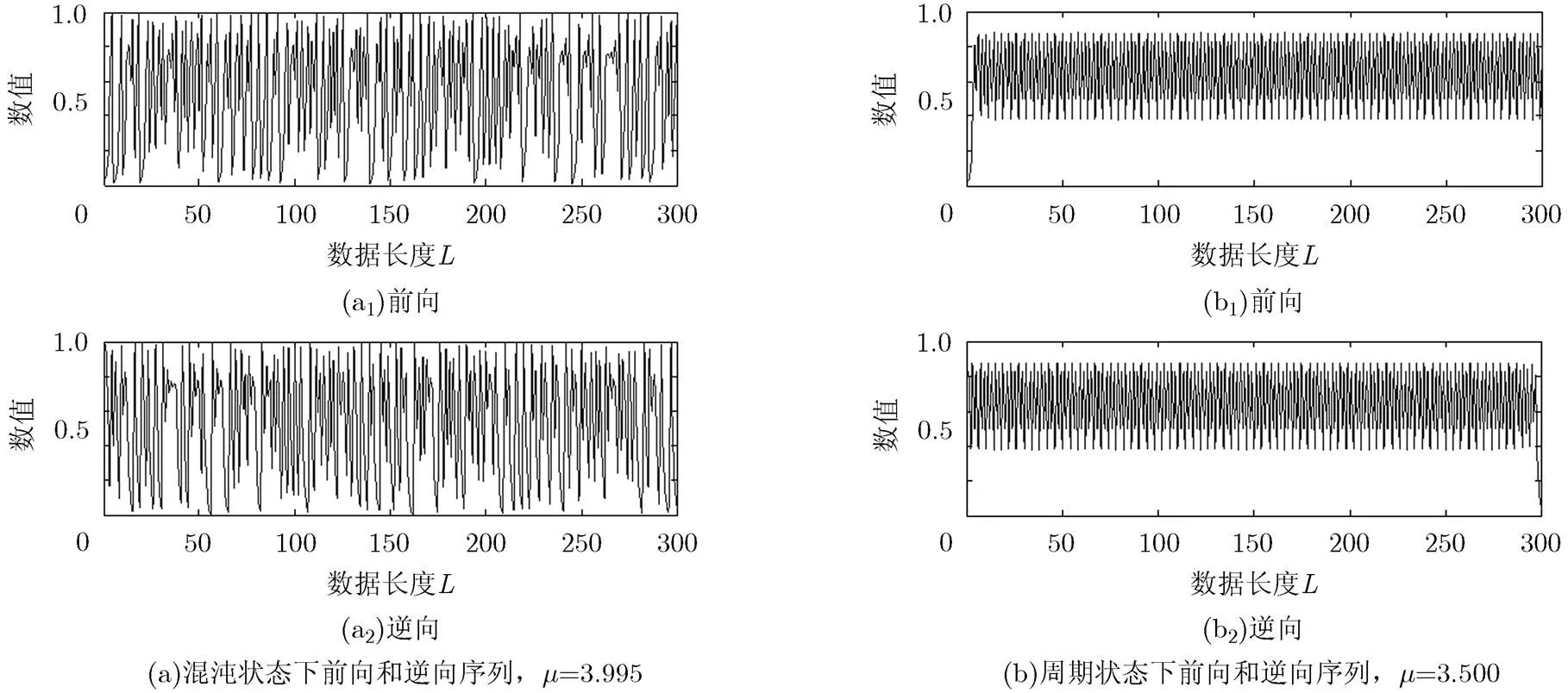
图5 Logistic混沌系统前向和逆向序列

图7 Logistic混沌系统相对熵与编码长度m的关系

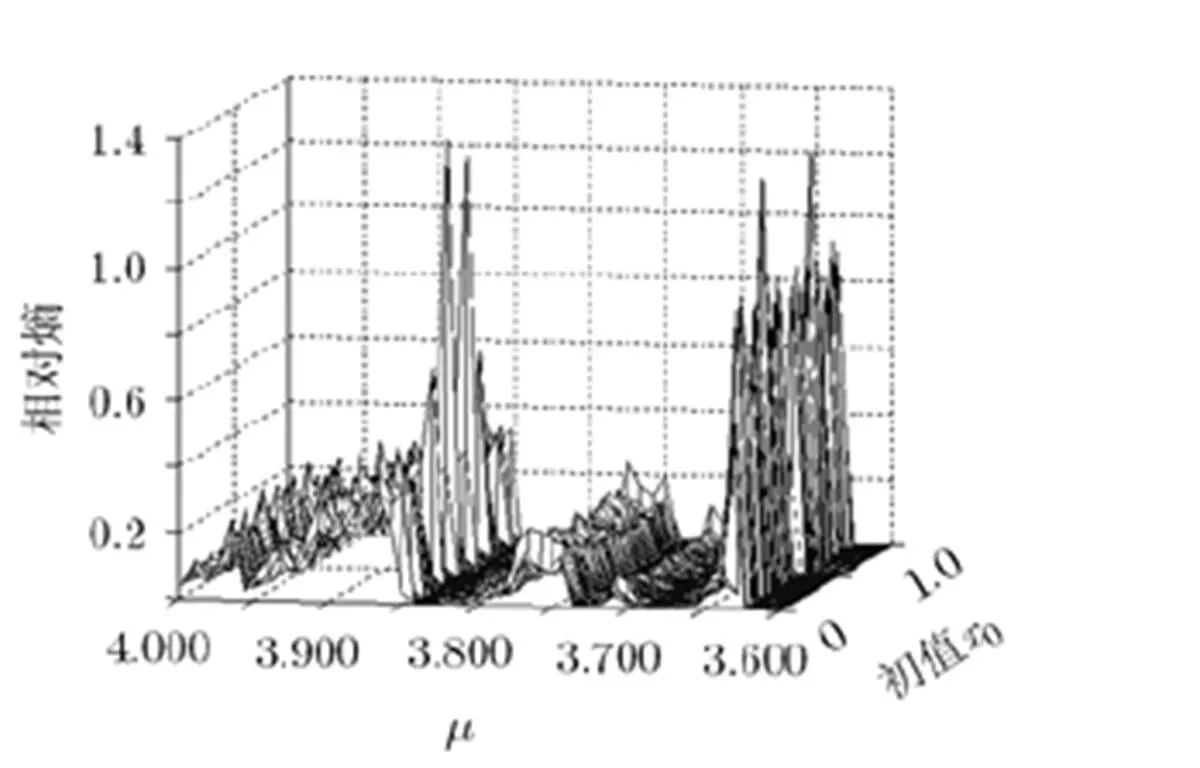
图8 L=5000, m=8, Logistic混沌系统符号序列相对熵3维图

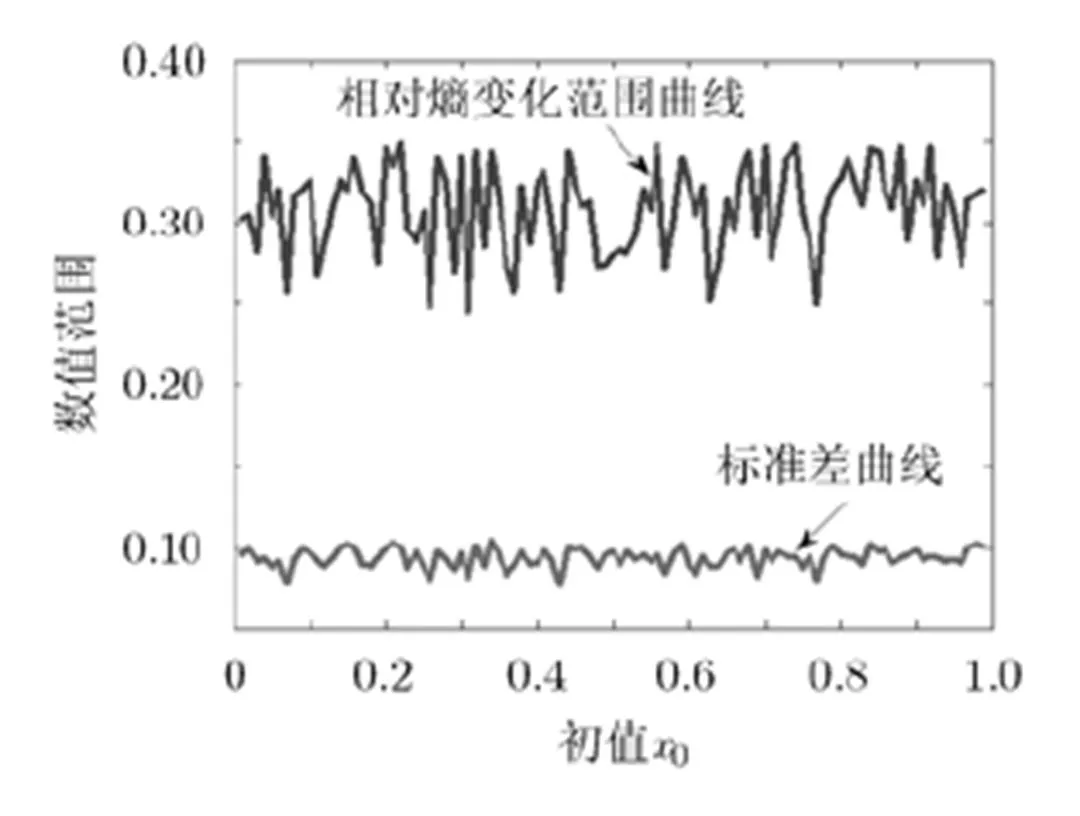
图9 Logistic混沌系统相对熵变化范围及相应标准差曲线

图10 L=5000, m=8, Logistic混沌系统序列分布图

4 结论

[1] Zhuang Qun-tao, Gao Xun, Ouyang Qi,.. Dynamical topology and statistical properties of spatiotemporal chaos[J]., 2012, 22(4): 043133.

[2] Wang Wen-xu, Yang Rui, Lai Ying-cheng,.. Predicting catastrophes in nonlinear dynamical systems by compressive sensing[J]., 2011, 106(4): 154101-1-154101-4.

[3] 郑建炜, 王万良, 蒋一波, 等. 概率型稀疏核Logistic多元分类机[J]. 电子与信息学报, 2011, 33(7): 1632-1638.

Zheng Jian-wei, Wang Wan-liang, Jiang Yi-bo,.. Probabilistic sparse kernel Logistic multi-classifier[J].&, 2011, 33(7): 1632-1638.

Hou Feng-zhen, Huang Xiao-lin, Zhuang Jian-jun,.. Multi-scale strategy and data surrogating test: two elements for the detection of time irreversibility in heart rate variabilities[J].,2012, 61(22): 220507-1-220507-6.

[5] Giaouris D, Banerjee S, Imrayed O,.. Complex interaction between tori and onset of three-frequency quasi-periodicity in a current mode controlled boost converter[J].,, 2012, 59(1): 207-214.

[6] Laugesen J L, Mosekilde E, and Zhusubaliyev Z T. Bifurcation structure of the-type period-doubling transition[J].:, 2012, 241(5): 488-496.

[7] Chen Yan-feng, Tse C K, Qiu Shui-sheng,.. Coexisting fast-scale and slow-scale instability in current-mode controlled DC/DC converters: analysis, simulation and experimental results[J]., 2008, 55(11): 3335-3347.

[8] De S, Dutta P S, and Banerjee S. Tours destruction in a nonsmooth noninvertible map[J]., 2012, 376(4): 400-406.

[9] Yao Tian-liang, Liu Hai-feng, Xu Jian-liang,.. Estimating the largest lyapunov exponent and noise level from chaotic time series[J]., 2012, 22(3): 033102.

[10] Kapat S, Patra A, and Banerjee S. Achieving monotonic variation of spectral composition in DC-DC converters using pulse skipping modulation[J]., 2011, 58(8): 1958-1966.

[11] 吴祥兴. 混沌学导论[M]. 上海: 上海科学技术文献出版社, 1997: 7-8.

[12] Packard J P, Crutchfield J P, Fanner J D,.. Geometry from a time series[J]., 1980, 45(9): 712-716.

[13] 杨林静, 戴祖诚. 噪声相互关联时间对Logistic系统亚稳态稳定性的影响[J]. 物理学报, 2012, 61(10): 100509-1-100509-4.

Yang Lin-jing and Dai Zu-cheng. The effects of correlated time between noises on stability of unstable state in logistic system[J]., 2012, 61(10): 100509-1-100509-4.

[14] 孙克辉, 贺少波, 何毅, 等. 混沌伪随机序列的谱熵复杂性分析[J]. 物理学报, 2013, 62(1): 010501-1-010501-8.

Sun Ke-hui, He Shao-bo, He Yi,.. Complexity analysis of chaotic pseudo-random sequences based on spectral entropy algorithm[J].,2013, 62(1): 010501-1-010501-8.

[15] 颜鹏程, 侯威, 胡经国. 基于Logistic模型的均值突变时间序列临界预警研究[J]. 物理学报, 2012, 61(18): 189202-1-189202-8.

Yan Peng-cheng, Hou Wei, and Hu Jing-guo. The critical warning research of the mean time series mutations based on Logistic model[J].,2012, 61(18): 189202-1-189202-8.

[16] Porporato A, Rigby J R, and Daly E. Irreversibility and fluctuation theorem in stationary time series[J]., 2007, 98(9): 094101-1-09410-14.

[17] 张梅, 王俊. 基于改进的符号相对熵的脑电信号时间不可逆性研究[J]. 物理学报, 2013, 62(3): 038701-1-038701-5.

Zhang Mei and Wang Jun. Modified symbolic relative entropy based electroencephalogram time irreversibility analysis[J].,2013, 62(3): 038701-1-038701-5.

[18] Roldán E and Parrondo J M R. Estimating dissipation from single stationary trajectories[J]., 2010, 105(15): 150607-1-150607-4.

[20] Wang Xue-mei, Zhang Bo, and Qiu Dong-yuan. The Quantitative characterization of symbolic series of a boost converter[J]., 2011, 26(8): 2101-2105.

[21] Rached Z, Alajaji F, and Campbell L L. The Kullback-Leibler divergence rate between markov sources[J]., 2004, 50(5): 917-921.

[22] 潘欣裕, 赵鹤鸣. Logistic 混沌系统的熵特性研究[J]. 物理学报, 2012, 61(20): 200504-1-200504-7.

Pan Xin-yu and Zhao He-ming. Research on the entropy of logistic chaos[J].,2012, 61(20): 200504-1-200504-7.

徐红梅：女，1975年生，博士生，研究方向为智能开关变换及控制、混沌动力学、无线通信技术.

郭树旭：男，1959年生，教授，博士生导师，研究方向为数字图像处理、高功率半导体激光器、无线通信技术.

Time Irreversibility Analysis of Logistic Chaos System Based on Symbolic Relative Entropy

Xu Hong-mei①②Guo Shu-xu①

①(,,130012,)②(,,133002,)

Chaos system; Logistic system; Symbolic time series; Relative entropy; Time irreversibility

TM132

1009-5896(2014)05-1242-05

10.3724/SP.J.1146.2013.01262