11轮3D密码的不可能差分攻击

谢作敏 陈少真 鲁林真



11轮3D密码的不可能差分攻击

谢作敏*陈少真 鲁林真

(解放军信息工程大学 郑州 450001) (数学工程与先进计算国家重点实验室 郑州 450001)

分组密码；不可能差分攻击；3D密码；预计算技术

1 引言

2008年，文献[1]提出3D密码算法。其设计原理来源于美国高级加密标准AES，它的分组长度与密钥长度都为512 bit，一共有22轮，AES采用的是2维的4×4的字节矩阵，而3D密码算法采用了3维4×4×4的字节矩阵。由于3D密码新的设计理念，加上现代科学技术的发展以及计算能力的不断刷新，分组密码的趋势必然是朝向更长的分组以及密钥长度发展，出于其安全性以及潜在应用考虑，该密码算法备受关注。

不可能差分攻击最先由文献[2,3]提出，用来分析DEAL与Skipjack算法。目前，不可能差分攻击被广泛地应用到了各种结构的分组密码攻击中，在AES[4], CLEFIA[5], MISTY1[6], Camellia[7]等密码上有非常好的攻击效果。近年来，不可能差分攻击也有了一些新的扩展与发展，文献[8]利用相关密钥不可能差分攻击方法攻击了8轮的AES-192, 2010年，文献[9]提出了不可能的概率差分攻击方法得到CLEFIA的最优攻击结果。

对3D密码的安全性分析最先由设计者Nakahara[1]提出。2010年文献[10]提出了最大可以扩展到9轮的3D密码的Square攻击。接着文献[11]提出了9轮不可能差分攻击。文献[12]在2011年提出了10轮不可能差分攻击。2012年，文献[13]提出了10轮3D密码的中间相遇攻击，与此同时文献[14]提出利用截断差分攻击首次实现了存在概率的对11轮3D密码的攻击。在今后的若干年，3D密码的研究仍然将是一个热点。

本文在不可能差分路径的选取以及密钥恢复过程中的数据处理做了若干提升：为了使不可能差分扩展到更多的轮数，在6轮不可能差分区分器的构造过程中，发现了一类较优的差分路径；在排除错误猜测密钥的过程中，利用预计算技术，将重复的加解密运算通过查表完成，大大减少了时间复杂度；初始化一部分猜测密钥，结合盒的可逆性质，建立部分轮子密钥与选择明文对的Hash表，使得在最后错误密钥排除过程中不用存储所有的猜测密钥，降低攻击所需的存储；为了恢复出主密钥，预留一部分没有排除掉的错误轮子密钥，再穷举另外一部分轮子密钥，以达到部分减少时间复杂度的目的。

本文的结构安排如下：第2节简要介绍3D密码的加密算法以及一些性质；第3节描述3D密码的一类新的6轮不可能差分区分器；第4节介绍3D密码的11轮不可能差分攻击；第5节给出了3D密码的10不可能差分攻击；第6节是结束语。

2 3D密码算法介绍

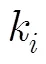
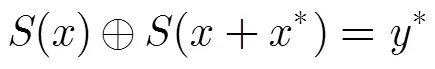
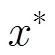
表1 3D密码S盒差分分布表

3 3D密码算法的6轮不可能差分区分器

为了使攻击达到更高的轮数，在不可能差分区分器首尾字节的选取上进行了优化筛选。如图1所示，此不可能差分区分器由两段构成，前3轮差分以及后3轮分别以概率1成立，而它们在中间相遇产生矛盾(由图1矛盾显然，具体证明略)，从而构成6轮不可能差分区分器。图1中“*”表示活动的非零字节差分值，“?”表示未知的差分值。第6轮中的轮密钥加与下一轮的列混合进行了交换。

性质3(一类6轮不可能差分区分器) 对3D密码的第偶数轮输入，如果满足4个子块中的任意一个子块中的其中两列中的3行为活动差分字节，而其它的58个字节差分值为零，经过6轮加密后，不可能出现输出状态有1个字节差分非零，而其它的字节差分值为零的情况。

图1 6轮不可能差分区分器

图2 一类6轮不可能差分区分器

4 对11轮3D密码的不可能差分攻击

4.1 预计算过程

本小节，建立5类Hash表用来分别提取密钥，将密钥恢复过程中的加解密过程通过查表完成，可以很好降低时间复杂度。

4.2 11轮3D密码的密钥恢复攻击过程

4.3 对11轮3D密码攻击的复杂度分析

5 对10轮3D密码的不可能差分攻击

本节在图3的11轮不可能差分路径的基础上，开展对3D密码的10轮不可能差分攻击。考虑到加解密结构的相似性，本节将逆向图3的11轮不可能差分路径，即图3中的第11轮为本攻击的第1轮，图3中的第2轮为本攻击的第10轮(最后一轮)。根据加解密相似性，对于图1构造的6轮不可能差分，倒过来，也是显然成立的。具体攻击路径如图4所示。

图3 3D密码的11轮不可能差分攻击路径

6 结束语

本文实现了对10轮与11轮的3D密码不可能差分攻击。表2列出了本文的攻击结果并比较了以往相关文献的数据。

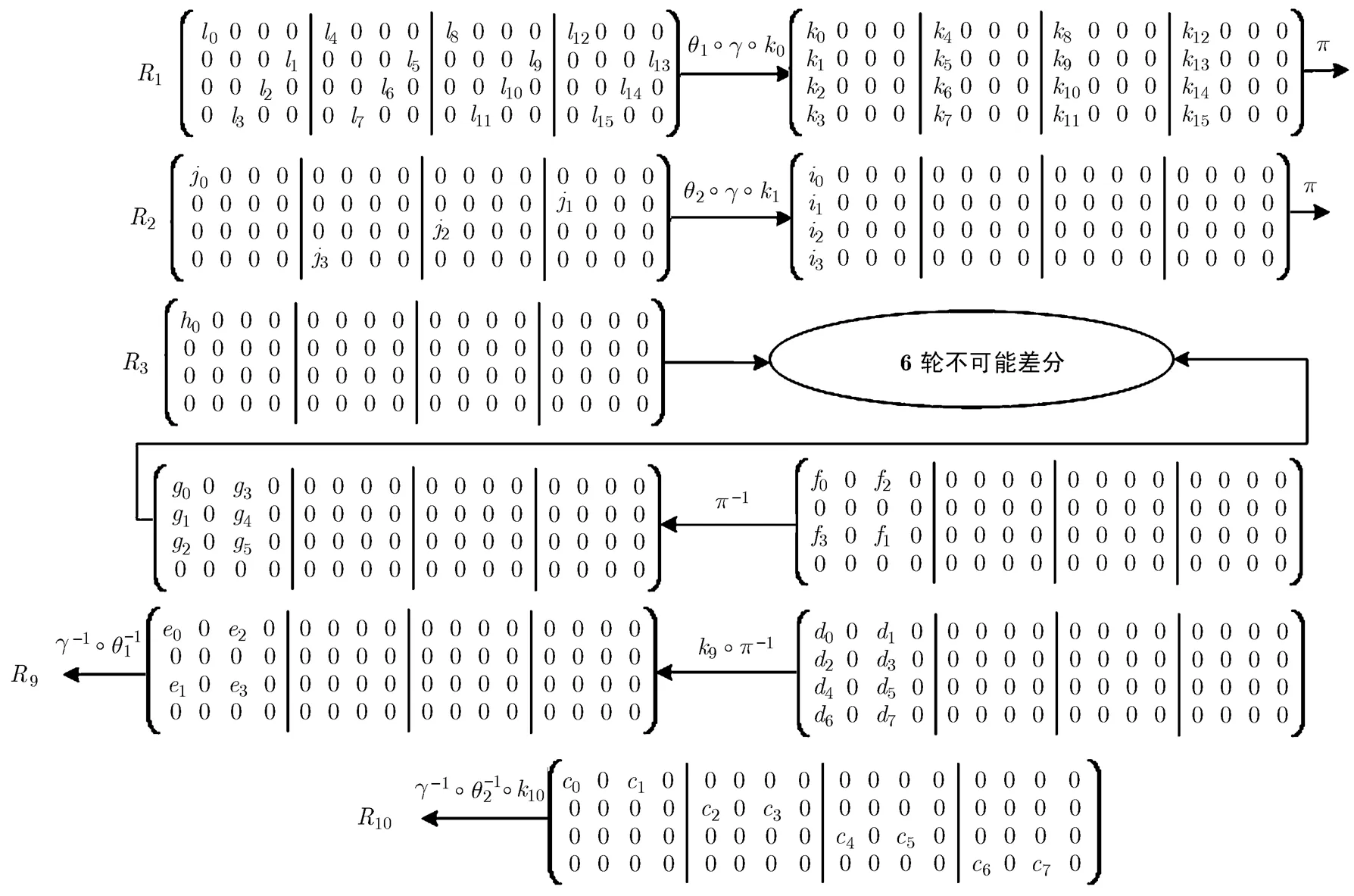
图4 3D密码的10轮不可能差分攻击路径

表2本文与部分3D密码攻击结果比较

轮数选择明文量时间复杂度存储(分组长度)攻击方法文献 7-IA[10] 7ID[11] 8-IA[10] 8ID[11] 9-IA[10] 9ID[11] 10ID[12] 102444.472318.82184.4ID本文 10MitM[13] 112493.032511.22388ID本文

ID：不可能差分攻击，MitM：中间相遇攻击，IA：积分攻击

本文较以往的对3D密码的攻击过程，在不可能差分区分器的首位字节位置选择上做了优化与筛选，同时利用预计算计算，利用S盒的输入输出差分计算出满足条件的输入输出对，通过查表分别计算猜测密钥的候选值，很大程度地减少了计算量，最终得以实现了3D密码的11轮攻击，足以说明用存储换取复杂度的思想是可行且有效的。而这种方法对于分组密码以及Hash算法的各种攻击，都提供了很好的优化思路。

[1] Nakahara J Jr. 3D: A three-dimensional block cipher[J]., 2008, 5339: 252-267.

[2] Knudsen L. DEAL-a 128-bit block cipher[J]., 1998, 258: 2-11.

[3] Biham E, Biryukov A, and Shamir A. Cryptanalysis of skipjack reduced to 31 rounds using impossible differentials [J]., 1999, 1592: 12-23.

[4] Liu Ya, Gu Dawu, Liu Zhi-qiang,.. New improved impossible differential attack on reduced-round AES-128[C]. Computer Science and Convergence , Springer-Verlag, Jeju, Korea, 2012, Vol. 114: 453-461.

[5] Mala H, Dakhilalian M, and Shakiba M. Impossible differential attacks on 13-round CLEFIA-128[J]., 2011, 26(4): 744-750.

[6] Jia K, Li L, Rechberger C,.. Impossible differential attacks on reduced-round MISTY1[J]., 2013, 7707: 222-233.

[7] Liu Y, Li L, Gu D,.. New observations on impossible differential cryptanalysis of reduced-round Camellia[J]., 2012, 7549: 90-109.

[8] Biham E and Dunkelman O. Related-key impossible differential attacks on 8-round AES-192[J]., 2006, 3860: 21-33.

[9] Cihangir Tezcan. The improbable differential attack: cryptanalysis of reduced-round CLEFIA[J]., 2010, 6498: 197-209.

[10] 王美一, 唐学海, 李超, 等. 3D密码的Square攻击[J]. 电子与信息学报, 2010, 32(1): 157-161.

Wang M Y, Tang X H, Li C,.. Square attacks on 3D cipher[J].&, 2010, 32(1): 157-161.

[11] 唐学海, 李超, 王美一, 等. 3D密码的不可能差分攻击[J]. 电子与信息学报, 2010, 32(10): 2516-2520.

Tang X H, Li C, Wang M Y,.. Impossible differential attack on 3D cipher[J].&, 2010, 32(10): 2516-2520.

[12] Nakahara J Jr. New impossible differential and known-key distinguishers for the 3D cipher[J]., 2011, 6672: 208-221.

[13] 苏崇茂, 韦永壮, 马春波. 10轮3D分组密码算法的中间相遇攻击[J]. 电子与信息学报, 2012, 34(3): 694-697.

Su Chong-mao, Wei Yong-zhuang, and Ma Chun-bo. Meet- in-the-middle attack on 10-round reduced 3D block Cipher[J].&, 2012, 34(3): 694-697.

[14] Takuma Koyama, Lei Wang, Yu Sasaki,.. New truncated differential cryptanalysis on 3D block cipher[J]., 2012, 7232: 109-125.

谢作敏： 男，1989年生，硕士生，研究方向为密码学与信息安全.

陈少真： 女，1967年生，博士生导师，研究方向为密码学与信息安全.

鲁林真： 男，1985年生，博士生，研究方向为密码学与信息安全.

Impossible Differential Cryptanalysis of 11-Round 3D Cipher

Xie Zuo-min Chen Shao-zhen Lu Lin-zhen

(,450001,) (,450001,)

Block cipher; Impossible differential attack; 3D cipher; Precomputation

TN918.1

A

1009-5896(2014)05-1215-06

10.3724/SP.J.1146.2013.00948

谢作敏 xiezuomin@126.com

2013-07-01收到，2013-12-16改回

信息保障技术重点实验室开放基金(KJ-13-010)资助课题